A processor design for singular value decomposition (SVD) and compression/decompression of feedback matrices, which are mandatory operations for SVD multiple-input multiple-output orthogonal frequency-division multiplexing (MIMO-OFDM) systems, is proposed and evaluated. SVD-MIMO is a transmission method for suppressing multistream interference and improving communication quality by beamforming. An application specific instruction-set processor (ASIP) architecture is adopted to achieve flexibility in terms of operations and matrix size. The proposed processor realizes a high-speed/low-power design and real-time processing by the parallelization of floating-point units (FPUs) and arithmetic instructions specialized in complex matrix operations.

1. Introduction

In recent years, multiple-input multiple-output orthogonal frequency-division multiplexing (MIMO-OFDM) has been attracting attention as a scheme for achieving high-speed and large-capacity wireless communications. MIMO-OFDM has been adopted for the current wireless LAN standard, IEEE 802.11n [1], and for the next-generation wireless LAN standard, IEEE 802.11ac [2].

It is possible to increase the communication capacity in MIMO systems by increasing the number of transmit and receive antennas; however, communication quality is degraded by the consequent multistream interference. As a solution to this degradation problem, singular value decomposition (SVD) MIMO systems are used. In the case of SVD-MIMO systems, it is possible to suppress multistream interference and to improve communication quality with beamforming using SVD [3]. The implementation of SVD by applying custom hardware processors has been reported in recent studies [4–7]. These processors provide high-speed calculation and enough accuracy for 4 × 4 SVD-MIMO systems. However, SVD-MIMO systems require not only SVD calculation but also other operations such as compression and decompression of feedback matrices [8] and should support a variety of matrix sizes depending on their configuration. Additionally, applying dedicated hardware only to SVD calculation is not superior in terms of utilization efficiency. Therefore, we have employed an application specific instruction-set processor (ASIP) architecture to achieve both flexibility and high processing efficiency. The ASIP implementation of QR decomposition supporting MIMO systems has been presented in [9]. However, it does not support SVD-MIMO systems.

This study mainly deals with 4 × 4 SVD-MIMO-OFDM systems; in particular, flexible processor supporting SVD of MIMO channel matrices and compression/decompression of feedback matrices was designed. The processor achieves efficient, real-time processing by parallelization of floating-point units (FPUs) and arithmetic instructions specialized in complex matrix operations. Since the processor employs an ASIP architecture and a floating-point data format, it can deal with other operations and larger matrix sizes (e.g., 8 × 8) while keeping high calculation accuracy. The improvement compared to our previous work [10] has been achieved by simplifying FPUs and optimizing calculation bit length. Additionally, a “packet-skip” method for reducing energy consumption and improving communication throughput is proposed and evaluated.

This paper is organized as follows. The theory of SVD-MIMO systems is explained in Section 2, and the algorithm of SVD and matrix compression/decompression is described in Section 3. Section 4 explains the structure of the proposed processor. Section 5 presents the evaluated performance of the designed circuit. The packet-skip method is explained and evaluated in Section 6. Section 7 presents the conclusions drawn from this study.

2. SVD-MIMO System

In an MIMO system with N transmit antennas and receive antennas, a transmission signal, x ∈ ℂ^N×1 goes through a propagation, H ∈ ℂ^N×N. A received signal, y ∈ ℂ^N×1, is expressed as

()

where n ∈ ℂ^N×1 is white Gaussian noise. A block diagram of an SVD-MIMO-OFDM system is illustrated in Figure 1. An SVD-MIMO system assumes that channel-state information (CSI) is known in a transmitter and a receiver. By SVD, the channel matrix, H, is decomposed into a diagonal matrix, Σ, and two unitary matrices, U and V, as

()

By beamforming using a transmit-weight matrix, V, the received signal is expressed as

()

In addition, by applying a receive-weight matrix, U^H, the received signal is finally expressed as

()

where Σ is a diagonal matrix having singular values of H in the diagonal elements. The receiver can therefore receive the signal without multistream interference.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

SVD-MIMO-OFDM system.

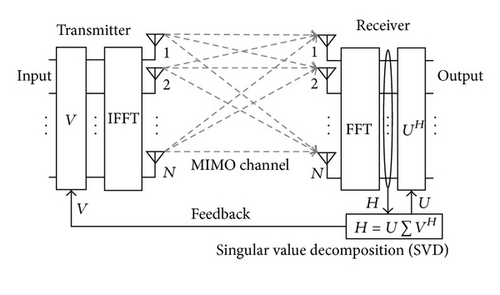
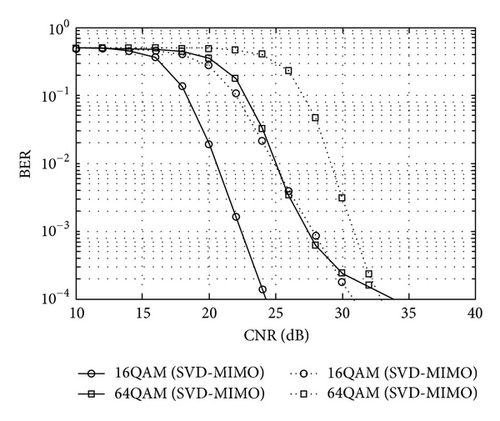
To investigate the effect of SVD-MIMO on improving transmission performance, bit error rates (BERs) of space-division multiplexing (SDM) MIMO without beamforming and of SVD-MIMO are compared by a baseband simulation. A 4 × 4 MIMO-OFDM system was used for this BER comparison. The simulation parameters are listed in Table 1 and the characteristics of SDM-MIMO and SVD-MIMO are compared in Figure 2. The figure shows that the beamforming by SVD-MIMO gains about 3 to 5 dB in carrier to noise ratio (CNR) for BER of 10⁻³.

Table 1. Simulation parameters.

Channel bandwidth	40 MHz
Number of FFT/IFFT points	128
Number of data subcarriers	108
Guard-interval duration	800 ns
Packet size	500 bytes
Modulation mode	16QAM, 64QAM
Coding rates	3/4
MIMO-channel model	TGn channel model D
Feedback-channel model	Ideal

3. Algorithm

3.1. Singular Value Decomposition

SVD is a method of matrix decomposition in linear algebra. By SVD, channel matrix H ∈ ℂ^N×N is decomposed as

()

where Σ is an N × N diagonal matrix, and its diagonal elements are called singular values:

()

U and V are N × N unitary matrices. The columns of U and V are, respectively, called “left singular vectors” and “right singular vectors.” The SVD of H = UΣV^H is calculated in the following three steps.

(a)
Bidiagonalization : calculate upper bidiagonal matrix B by bidiagonalization using a Householder transformation.
(b)
SVD of bidiagonal matrix : execute eigenvalue decomposition of by a QR algorithm and calculate U₂ = BV₂Σ⁻¹ from V₂, Σ.
(c)
Inverse transform U = U₁U₂, V = V₁V₂: calculate unitary matrices U and V from U₁ and U₂ and V₁ and V₂, respectively, in steps (a) and (b).

3.1.1. Eigenvalue Decomposition by QR Algorithm

QR is an algorithm for calculating the eigenvalues of a matrix. It executes the QR decomposition iteratively. The QR decomposition decomposes a matrix into a product of a unitary matrix, Q, and an upper triangle matrix, R. QR is executed by repeating the following operations:

()

Since this iterative process is a similarity transformation, the eigenvalues of X₀, …, X_m+1 are all equal. When X is a Hermitian matrix, X_m+1 converges to a diagonal matrix, and the eigenvalues are obtained. When X_k is a tridiagonal matrix, X_k+1 is also a tridiagonal matrix. In the case of SVD calculation, matrix X = B^HB is a tridiagonal Hermitian matrix. X_m+1 therefore converges to diagonal matrix Σ²:

()

The Givens rotation algorithm (which is the linear transformation by the matrix for the QR decomposition) is adopted, and the number of iterations in the QR algorithm is set to 10.

3.2. Feedback-Matrix Compression

A SVD-MIMO system has a drawback of which throughput is decreased by “matrix feedback.” To address this drawback, compression of the feedback matrix is effective. Accordingly, the compression method of a unitary matrix that is adopted in the IEEE 802.11n standard [1] is used. This method transforms a unitary matrix into angles by real transformation and the Givens rotation. It assumes that the Nth row of an N × N unitary matrix, V, is transformed into real numbers in the preprocessing. For V₁ = V, i = 1, a matrix, D_i, which transforms the ith column into real numbers is generated by

()

where ϕ_i,j is an argument of V_i at the ith row and jth column. By multiplying V_i by

, the ith column of V_i becomes real numbers. As a result, nondiagonal elements at the ith column in

become zero according to the Givens rotation. The Givens rotation matrix, G_ij, and its elements are generated by

()

By multiplying

and the Givens rotation matrices G_i+1,i, G _i+2,i, …, G_N,i, nondiagonal elements at the ith column in

become zero. Since V is a unitary matrix, nondiagonal elements at the ith row in

also become zero, and the element at the ith row and the ith column in

becomes one, which is expressed as

()

By repeating these processes for i = 2,3, …, N − 1, matrix V is finally transformed into an identity matrix, I_N. Here, applying (9) and (10) generates the real transformation matrix, D, and the Givens rotation matrix, G, from phases ϕ and ψ, respectively. Moreover, applying (13) makes it possible to compute V_i from V_i+1 as follows:

()

Since the receiver feeds back only phases ϕ and ψ, the feedback data is transformed from N² complex elements into N(N − 1) positive real phases. Table 2 compares the feedback data sizes between noncompressed data and compressed data. Each quantization bit rate is determined by a baseband simulation to avoid degradation of communication performance. In the case of noncompressed data, both the real part and the imaginary part are quantized in seven bits. On the other hand, in the case of compressed data, ϕ and ψ are quantized in seven bits and five bits, respectively.

Table 2. Comparison of feedback data sizes.

Noncompressed	Compressed
24192 bit	7776 bit

4. Processor Structure

An application specific instruction-set processor (ASIP) architecture has been employed for the processor architecture, and efficient processing and flexibility were achieved by preparing arithmetic instructions specialized in complex matrix operations.

4.1. Circuit Structure

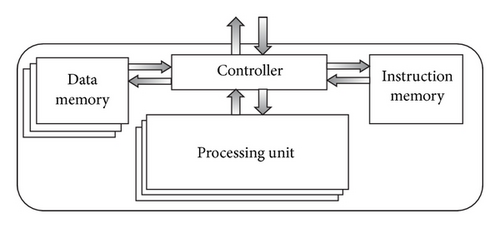
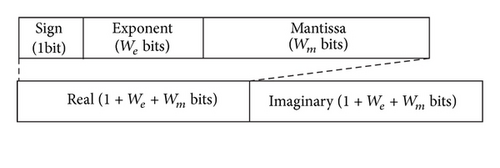
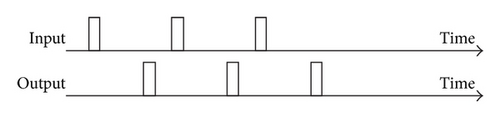
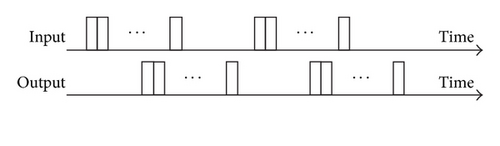
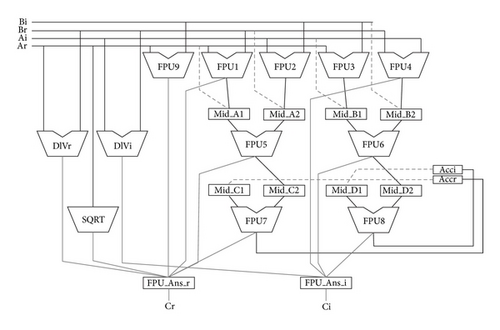
The circuit structure of the proposed processor is illustrated in Figure 3. Data and instructions are stored to each memory unit, and the processing unit executes instructions in order. The floating-point data format supports complex values, and each part of a complex value consists of a 1-bit sign part, a W_e-bits exponent part, and W_m-bits mantissa part, whose format is shown in Figure 4. Basically, each bit length is based on the IEEE 754 standard (W_e = 8, W_m = 23). Data memories and processing units are arrayed by the number of parallel processing. Two types of data transfers, which are shown in Figure 5, are supported. A single-data transfer sends data to the processing unit one by one. On the other hand, a block-data transfer sends data blocks containing multiple entries to the processing unit. The structure of the processing unit, which consists of nine floating-point units (FPUs) and dedicated circuits for division and square-root operation [11], is shown in Figure 6. “FPU1” to “FPU4” are used for multiplication, and “FPU5” to “FPU9” are used for addition and subtraction; in particular, “FPU9” is used for only CORDIC operations, which are described in Section 4.4. A variety of instructions can be executed by changing the data paths in the processing unit.

4.2. Instruction Format

The instruction format consists of memory addresses of input data A, B, output data C, and operation type, whose format is shown in Figure 7. The bit lengths are given as log ₂ N_DW bits and log ₂ N_OP bits, where N_DW is the number of data memory words, and N_OP is the number of instructions. Table 3 lists the instructions supported by the proposed processor.

Table 3. Instructions.

Index	Operation
0	Complex addition
1	Complex subtraction
2	Complex multiplication
3	Real multiplication
4	Accumulative complex addition
5	Accumulative complex subtraction
6	Accumulative complex multiplication
7	Accumulative real multiplication
8	Real division
9	Square-root operation
10	Squared absolute value
11	Accumulative squared absolute value
12	Hermitian multiplication
13	Initialization for the Newton method
14	Complex conjugate
15	Data copy
16	Initialization in CORDIC arctangent
17	Repetition in CORDIC arctangent
18	Initialization in CORDIC sine and cosine
19	Repetition in CORDIC sine and cosine
20	Merge real and imaginary parts
21	Extraction of real part
22	Extraction of imaginary part
23	Extraction of sign parts
24	Conversion from integer to floating-point format
25	Conversion from floating-point format to integer

4.3. Complex Operation

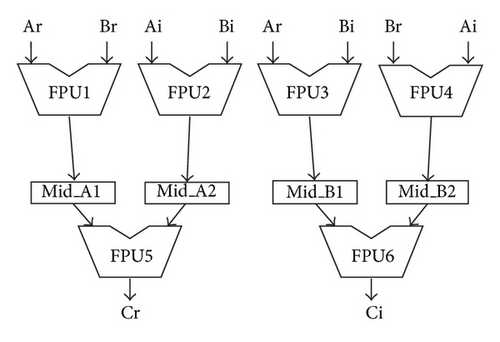
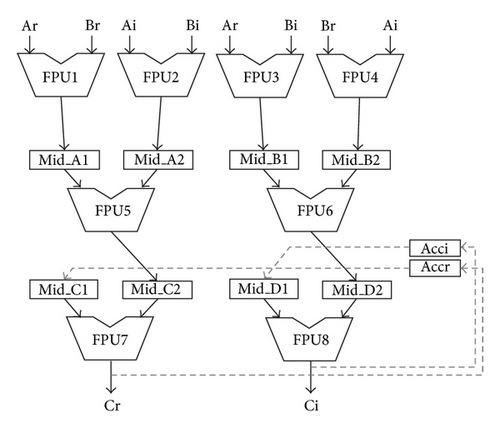
The proposed processor achieves efficient processing in complex matrix operations by adopting specialized instructions and an operation-unit structure. For instance, the complex multiplication of A × B = (A_r + jA_i)(B_r + jB_i) = (A_rB_r − A_iB_i) + j(A_rB_i + A_iB_r) = C_r + jC_i = C is executed in seven cycles using “FPU1” to “FPU4,” “FPU5,” and “FPU6” for multiplication, subtraction and addition, respectively, as shown in Figure 8. Moreover, the accumulative complex multiplication is executed in nine cycles using the registers of “Accr”, “Acci,” and “FPU7,” and “FPU8” as shown in Figure 9.

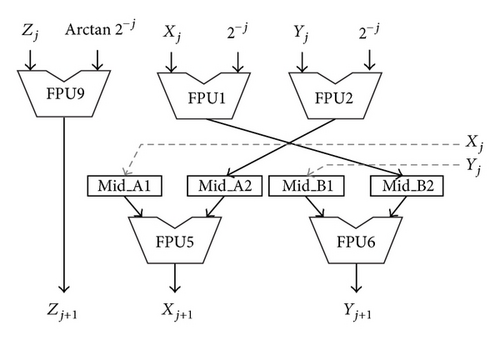
4.4. CORDIC Method

The proposed processor executes approximate calculation by the CORDIC (coordinate rotation digital computer) method for calculating trigonometric functions, which is necessary for the matrix compression and decompression. The recurrence formulas used in the CORDIC method are expressed by

()

By setting the initial values to

()

and selecting −1 or 1 for q_j so that Z_j+1 approaches zero, it is possible to calculate cosine and sine values as

()

On the other hand, setting the initial values to

()

and selecting −1 or 1 for q_j so that Y_j+1 approaches zero makes it possible to calculate an arctangent value as

()

To execute the CORDIC operations in the processing unit, five FPUs are used, as shown in Figure 10, where the signs of input data 2^−j, arctan2^−j at “FPU1,” “FPU2,” and “FPU9” are reversed depending on the condition. The values of 2^−j, arctan2^−j (j = 0,1, …, n − 1) are loaded from the data memory unit. And the number of iterations used with the CORDIC method is set to 10.

4.5. Division and Square-Root Operation

In the case that only “FPU1” to “FPU8” are used, the division and square-root operations are executed by approximate calculation using the Newton-Raphson method. However, they require 115 cycles and 1430 cycles, respectively. The implementation of dedicated circuits for division and square-root operation is effective for hardware acceleration. Division and square-root floating-point units [11] were therefore adopted. Since those units can execute division and square-root operation in 11 cycles, calculation time can be significantly reduced.

4.6. Bit-Length Optimization

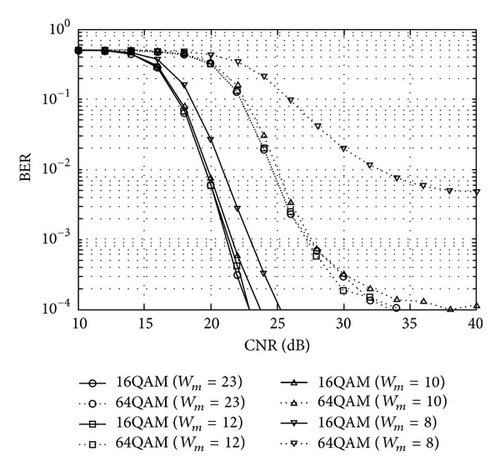
Since required precision depends on systems, circuit area and power consumption can be reduced by decreasing bit length. To optimize the mantissa bit length of the proposed processor for SVD and matrix compression/decompression, BER characteristics for several bit lengths were evaluated by simulation. The simulation parameters are the same as listed in Table 1, and the characteristics evaluation is shown in Figure 11. From this figure, the optimal mantissa bit length is taken as 12 bits.

5. Performance Evaluation

5.1. Circuit Design

The proposed processor was designed by using Verilog hardware description language and synthesized in the controller and the processing units by using a 90 nm CMOS standard cell library. The clock frequency was set to 400 MHz (2.5 ns in a clock period), and the supply voltage was set to 1.0 V.

5.2. Circuit Performance

The circuit performance was evaluated in cases with or without division and square-root units. The results are listed in Tables 4 and 5, respectively. The calculation time for all channel matrices of 108 data subcarriers was measured. The number of entries in the block data transfer was set to 18 to minimize energy consumption. According to these results, the implementation of the division and square-root units increases circuit area two-fold and power consumption by half. However, since the calculation time can be reduced to 1/7 ~ 1/9, energy consumption can be reduced to 1/4 ~ 1/6. This comparison shows that the implementation of division and square-root units is effective.

Table 4. Circuit performance with division and square-root units.

	Single	Block (18 entries)
Calculation time (ms)	6.33	1.16
(per matrix)	(0.06)	(0.01)
Gate count	82,376	90,885
Power consumption (mW)	22.1	39.4
Energy consumption (μJ)	139.9	45.8
(per matrix)	(1.3)	(0.4)

Table 5. Circuit performance without division and square-root units.

	Single	Block (18 entries)
Calculation time (ms)	46.92	10.45
(per matrix)	(0.43)	(0.10)
Gate count	38,688	47,390
Power consumption (mW)	13.5	25.4
Energy consumption (μJ)	633.0	265.1
(per matrix)	(5.9)	(2.5)

5.3. Bit-Length Limitation

In the previous section, circuit performance without bit length limitation (W_m = 23) was evaluated. In contrast, in this section, circuit performance with bit length limitation (W_m = 12) is evaluated (see Table 6). In this evaluation, division and square-root units were implemented and the bit-length limitation is applied in multipliers only, which account for large portion of the operation. This result shows that the bit-length limitation can reduce circuit area, power consumption, and energy consumption by about 10%, 20%, and 20%, respectively.

Table 6. Circuit performance with bit length limitation.

	Single	Block (18 entries)
Calculation time (ms)	6.33	1.16
(per matrix)	(0.06)	(0.01)
Gate count	73,564	81,943
Power consumption (mW)	18.5	30.8
Energy consumption (μJ)	117.0	35.8
(per matrix)	(1.1)	(0.3)

5.4. Processing Time

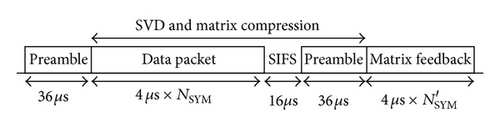
A timing chart of the SVD-MIMO-OFDM system is shown in Figure 12. It is assumed that the update and feedback of CSI are executed at every packet. The calculation of SVD and the matrix compression must be completed between receiving the preamble of the data packet and sending the feedback-matrix data. When the number of OFDM data symbols, N_SYM, is 50, the acceptable calculation time is 252 μs. When the proposed processor arrays six processing units by parallel processing, it takes 193 μs for SVD and matrix compression. Since the calculation time is less than the acceptable calculation time, the processor realizes real-time processing.

5.5. Comparison with Related Works

The proposed processor is compared here with our previous work [10] and other related works [4–6] in Table 7. Compared with our previous work, the proposed processor has improved throughput by almost four times, even though it also performs matrix compression. This improvement was achieved by simplifying FPUs and imposing the bit-length limitation. In consideration of SVD operation only, the performance of the proposed processor is not superior to that of either [5] or [6]. However, it can realize sufficient real-time processing and support not only SVD but also matrix compression and decompression (MCD). It therefore achieves faster communication throughput than the other processors. Furthermore, since the proposed processor employs an ASIP architecture and floating-point data format, it can deal with other operations and larger matrix sizes while keeping high calculation accuracy. Given these advantage features, it is concluded that the proposed processor can realize an SVD-MIMO-OFDM system more effectively than the other processors.

Table 7. Performance comparison.

	[4]	[5]	[6]	[10]	Proposed
Architecture	Custom	Custom	Custom	ASIP	ASIP
Data type	fixed point	fixed point	fixed point	floating point	floating point
Matrix size	4 × 4	4 × 4	4 × 4	4 × 4	4 × 4
CMOS process	90 nm	0.18 μm	90 nm	90 nm	90 nm
Gate count	900 k	42.3 k	120 k	83.7 k	81.9 k
Clock frequency (MHz)	500	149	182	400	400
Throughput (matrices/s)	125 k	303 k	7 M	25 k	93 k
Calculation time (μs/matrix)	8	3.3	0.14	40	10.8
Utilization efficiency (throughput/gate count)	0.15	7.16	59.52	0.29	1.13
Supported operations	SVD	SVD	SVD	SVD	SVD, MCD
Size of side information	Large	Large	Large	Large	Compressed

6. Packet-Skip Method

As explained in the previous sections, it was assumed that the system feeds back the weight matrix at every packet. However, if the channel state is changed gradually, it is possible to skip the SVD calculation and the feedback of the weight matrix and to apply the previous weight matrix without degradation of BER. On the basis of this idea, energy consumption can be reduced and communication throughput can be increased by skipping the SVD calculation and the weight-matrix feedback.

6.1. Simulation

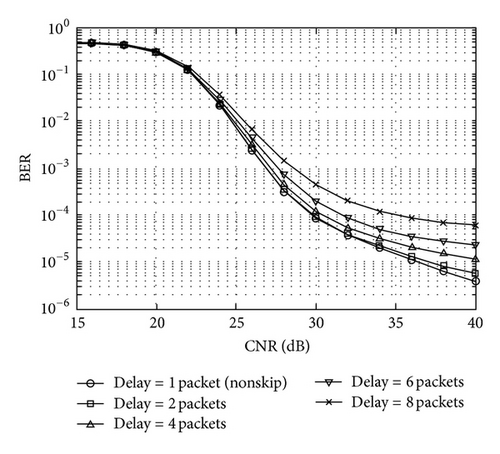
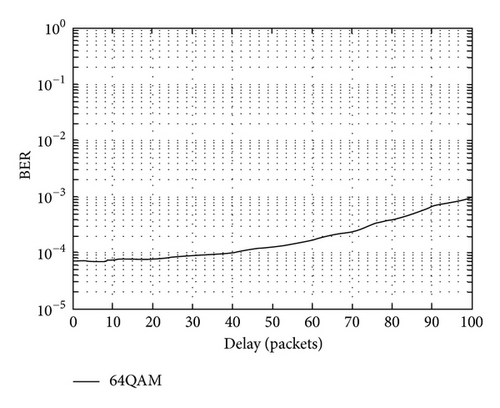
To determine the optimal skip number, BER characteristics for several numbers of packet skips were evaluated by simulation. The simulation assumed a communication environment with the 10 Hz Doppler frequency. The simulation parameters are listed in Table 8, and the BER evaluation result is shown in Figure 13. The delay in this figure means the numbers of packet skips. The packet skip is applied from the packet at which the SVD calculation process starts to the packet to which weight matrices are applied. According to this figure, a delay of less than 5 packets is acceptable under this communication environment. Additionally, BER characteristics in a communication environment with the 1 Hz Doppler frequency were evaluated. The simulation parameters are listed in Table 9, and the BER evaluation result is shown in Figure 14. According to this figure, a delay within 30 to 40 packets is acceptable under this communication environment.

Table 8. Simulation parameters.

Channel bandwidth	40 MHz
Number of FFT/IFFT points	128
Number of data subcarriers	108
Guard-interval duration	800 ns
Number of OFDM symbols	50
Modulation mode	64QAM
Coding rates	3/4
MIMO-channel model	TGn channel model D
Doppler frequency	10 Hz
Feedback-channel model	Ideal

Table 9. Simulation parameters.

Channel bandwidth	40 MHz
Number of FFT/IFFT points	128
Number of data subcarriers	108
Guard-interval duration	800 ns
Number of OFDM symbols	50
Modulation mode	64QAM
Coding rates	3/4
MIMO-channel model	TGn channel model D
Doppler frequency	1 Hz
CNR	30 dB
Feedback-channel model	Ideal

6.2. Skip Method

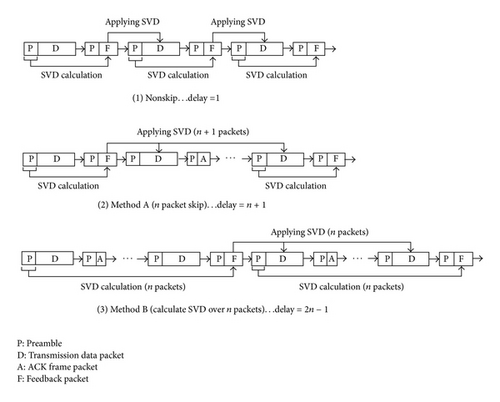
For packet skipping, two methods (illustrated schematically in Figure 15) are proposed. As for the first method, that is, method A, SVD calculation is executed over one packet and the weight matrices are applied to the next (n + 1) packets. The delay produced by method A is (n + 1) packets. On the other hand, as for the second method, that is, method B, SVD is calculated over n packets, and the weight matrices are applied to the n packets after the SVD calculation. The delay produced by method B is (2n − 1) packets. In the case of method A, total energy consumption is reduced by 1/(n + 1). In the case of method B, the power consumption can be reduced since the calculation time of SVD is longer than that of the nonskip system or method A.

6.3. Performance Evaluation

Circuit performance and communication throughput when these skip methods were applied was evaluated. In the evaluation, it was assumed that the delay is 5 packets for a communication environment with the 10 Hz Doppler frequency. Accordingly, n = 4 and 3 for methods A and B, respectively. The results of the performance evaluation are listed in Table 10. In the evaluation, communication throughput was calculated under the assumption that signals are transmitted by 4 × 4 SVD-MIMO (64QAM, R = 3/4, and 50 symbols) and the feedbacks are transmitted by 4 × 4 SDM-MIMO (16QAM, R = 3/4). According to these performance results, method A is the most effective in terms of energy consumption and communication throughput.

Table 10. Performance evaluation.

	Nonskip	Method A	Method B
Acceptable calculation time (μs)	252	252	836
Number of parallel ASIPs	6	6	2
Calculation time (μs)	193.7	193.7	581.2
Energy consumption (per packet) (μJ)	35.82	7.16	11.94
Communication throughput (Mbps)	292.8	324.0	318.3

7. Concluding Remarks

A processor design for SVD-MIMO-OFDM systems was proposed. The proposed processor employs an ASIP architecture and achieves both flexibility and high throughput by parallelization of FPUs and arithmetic instructions that are specialized in complex matrix operations. In addition, two types of packet-skip method for reducing energy consumption and increasing communication throughput were proposed. In future work, we will deal with larger-scale SVD-MIMO-OFDM systems (e.g., 8 × 8 SVD-MIMO).

References

1 IEEE Std 802.11n-2009 Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications, October 2009.
Google Scholar
2 Stacey R., Specification Framework for TGac, IEEE802.11 document 09/0992r15, September 2010.
Google Scholar
3 Goldsmith A., Jafar S. A., Jindal N., and Vishwanath S., Capacity limits of MIMO channels, IEEE Journal on Selected Areas in Communications. (2003) 21, no. 5, 684–702, 2-s2.0-0038236418, https://doi.org/10.1109/JSAC.2003.810294.
Google Scholar
4 Markovic D., Brodersen R. W., and Nikolic B., A 70GOPS, 34mW multi-carrier MIMO chip in 3.5mm², Proceedings of the IEEE Symposium on VLSI Circuits (VLSIC ′06), June 2006, 158–159, 2-s2.0-38049060354.
Google Scholar
5 Senning C., Studer C., Luethi P., and Fichtner W., Hardware-efficient steering matrix computation architecture for MIMO communication systems, Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS ′08), May 2008, 304–307, 2-s2.0-51749086018, https://doi.org/10.1109/ISCAS.2008.4541415.
Google Scholar
6 Zhan C.-Z., Chen Y.-L., and Wu A.-Y., Iterative superlinear-convergence SVD beamforming algorithm and VLSI architecture for MIMO-OFDM systems, IEEE Transactions on Signal Processing. (2012) 60, no. 6, 3264–3277.
Google Scholar
7 Chen Y.-L., Zhan C.-Z., Jheng T.-J., and Wu A.-Y., Reconfigurable adaptive singular value decomposition engine design for high-throughput MIMO-OFDM systems, IEEE Transactions on Very Large Scale Integration (VLSI) Systems. (2012) no. 99, 1.
Google Scholar
8 Studer C., Luethi P., and Fichtner W., VLSI architecture for data-reduced steering matrix feedback in MIMO systems, Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS ′08), May 2008, 300–303, 2-s2.0-51749118722, https://doi.org/10.1109/ISCAS.2008.4541414.
Google Scholar
9 Salmela P., Burian A., Sorokin H., and Takala J., Complex-valued QR decomposition implementation for MIMO receivers, Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP ′08), April 2008, 1433–1436, 2-s2.0-51449086843, https://doi.org/10.1109/ICASSP.2008.4517889.
Google Scholar
10 Yoshizawa S., Kaji T., and Miyanaga Y., Low-energy ASIP implementation of singular value decomposition for MIMOOFDM systems, Proceedings of the International Conference on Embedded Systems and Intelligent Technology (ICESIT ′12), February 2012, 180–183.
Google Scholar
11 Oberman S. F. and Flynn M. J., Design issues in division and other floating-point operations, IEEE Transactions on Computers. (1997) 46, no. 2, 154–161, 2-s2.0-0031076832.
Google Scholar

Citing Literature

All articles

A High-Speed and Low-Energy-Consumption Processor for SVD-MIMO-OFDM Systems

Abstract

1. Introduction

2. SVD-MIMO System

3. Algorithm

3.1. Singular Value Decomposition

3.1.1. Eigenvalue Decomposition by QR Algorithm

3.2. Feedback-Matrix Compression

4. Processor Structure

4.1. Circuit Structure

4.2. Instruction Format

4.3. Complex Operation

4.4. CORDIC Method

4.5. Division and Square-Root Operation

4.6. Bit-Length Optimization

5. Performance Evaluation

5.1. Circuit Design

5.2. Circuit Performance

5.3. Bit-Length Limitation

5.4. Processing Time

5.5. Comparison with Related Works

6. Packet-Skip Method

6.1. Simulation

6.2. Skip Method

6.3. Performance Evaluation

7. Concluding Remarks

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley