Sliding Intermittent Control for BAM Neural Networks with Delays
Abstract
This paper addresses the exponential stability problem for a class of delayed bidirectional associative memory (BAM) neural networks with delays. A sliding intermittent controller which takes the advantages of the periodically intermittent control idea and the impulsive control scheme is proposed and employed to the delayed BAM system. With the adjustable parameter taking different particular values, such a sliding intermittent control method can comprise several kinds of control schemes as special cases, such as the continuous feedback control, the impulsive control, the periodically intermittent control, and the semi-impulsive control. By using analysis techniques and the Lyapunov function methods, some sufficient criteria are derived for the closed-loop delayed BAM neural networks to be globally exponentially stable. Finally, two illustrative examples are given to show the effectiveness of the proposed control scheme and the obtained theoretical results.
1. Introduction
Since the bidirectional associative memory (BAM) neural networks were first proposed by Kosko [1] which are well known as the extension of the unidirectional autoassociators such as the Hopfield neural networks, they have been widely studied due to their extensive applications such as pattern recognition, signal or image processing, solving optimization problems, and automatic control [2–7]. Later, constant delays are introduced in [8] to the BAM neural networks, and it is proved that the delayed versions of the neural networks are significant for handling certain motion-related optimization problems [9]. For more results concerning the dynamical behaviors of the BAM neural networks with delays, we refer to [10, 11].
In practice, most of the neural networks are unstable or convergent with a rate far less than the requirement. Under such cases we need to try to stabilize them or speed up the convergence rate of the neural system in order to make the system work more efficiently. Therefore, the designing of appropriate control input becomes extremely urgent. When it comes to the problem of stabilizing a nonlinear system, it is natural to consider the feedback strategies. There are two basic kinds of feedback control: the state feedback control and the output feedback control. When referring to the control methods, different kinds of schemes have been utilized to stabilize the nonlinear system such as static feedback control [12], delayed feedback control [13], adaptive control [14], fuzzy control [15], sampled control [16], sliding mode control [17], and random control [18, 19]. In terms of the control time, the controllers are classified with continuous control and discontinuous control. Compared with the continuous control, the discontinuous control including the impulsive control [20, 21] and the intermittent control [22, 23] has attracted much more attention, and it is very effective, practical, and applicable in many areas, especially in secure communication [24].
In the literature, the impulsive neural networks have been extensively studied from the following two aspects: either the system is subject to the impulsive state displacements at fixed time instants or the system is imposed by external impulsive control [25]. The main idea of periodically intermittent control [26] is that when the system signal becomes weak to a low level, the external control will be imposed to supplement the loss of signal; after some period of time the external control is stopped; in the next control period the external control is needed again. Compared with the method of periodically intermittent control, the system with the impulsive control is activated only at some isolated time moments. Both the impulsive control and the intermittent control have their own benefits and disadvantages. The main difference between these two control techniques lies in the length of control period; the former has zero duration, while the later has a nonzero control width. Meanwhile, the cost of the intermittent control is much higher.
The aim of this paper is to design a sliding intermittent controller by combining the advantages of both the impulsive control and the periodically intermittent control. More specifically, in one control period, we will impose the continuous state feedback control at the preceding control width and the impulsive control in the latter control width. The sliding intermittent control method is very flexible and could achieve the expected control performance. The sketch of such a controller is shown in Figure 1. Motivated by the name of the slide rheostat in the physical electronic circuitry, we named such a joint controller as the sliding intermittent controller.
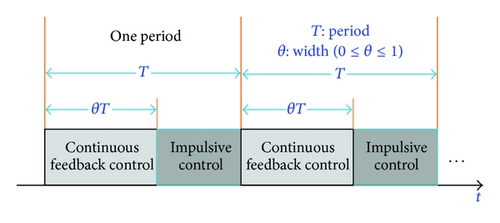
In this paper, we will investigate the exponential stability problem of the delayed BAM neural networks under the proposed sliding intermittent control. The closed-loop neural system becomes a switched network where the switching rules are dependent on the time index. To the best of the authors’ knowledge, this is the first time in the literature to consider such a joint controller. The rest of the paper is organized as follows. In Section 2, the model discussed in this paper and the novel sliding intermittent control idea are introduced, and some preliminaries are also given. In Section 3, several sufficient criteria are established to ensure the delayed BAM neural networks to be exponentially stable under the sliding intermittent control scheme. Meanwhile, several particular cases are discussed. In Section 4, two illustrative examples are given to demonstrate the effectiveness of the proposed results. And finally, the paper is concluded in Section 5.
2. Problem Formulation and Some Preliminaries
Remark 1. The above conditions are general in the literature to study the existence and uniqueness of the equilibrium for the delayed BAM neural networks (1) without assuming the activation functions to be monotonic or differentiable [27–29].
Letting (w*, z*) with and be an equilibrium of the system (1) and denoting, the equilibrium of the network (1) can be transformed to the origin of the following system:
Remark 2. The sliding intermittent control idea is illustrated in Figure 1 with the adjustable parameter θ (i.e., the control width θ shown in Figure 1). The closed-loop system (4) can be the continuous controlled neural networks (θ = 1), the impulsive controlled neural networks (θ = 0), or the hybrid controlled neural networks (0 < θ < 1).
The system (4) is supplemented with initial function given by xi(s) = φi(s), yj(s) = ψj(s), − τ* ≤ s ≤ 0, where φ(s) = (φ1(s), φ2(s), …, φn(s)) T ∈ C([−τ*, 0], ℝn), ψ(s) = (ψ1(s), ψ2(s), …, ψm(s)) T ∈ C([−τ*, 0], ℝm), and C([−τ*, 0], ℝn) represents the set of all n-dimensional continuous functions defined on the interval [−τ*, 0]. Obviously, the solution of (4) is piecewise left-hand continuous with possible discontinuity at t = tk for k ∈ ℕ+.
The following definition and lemmas are introduced before we give the main results of the paper.
Definition 3. The system (4) is said to be globally exponentially stable if there exist constants α > 0, β > 0 such that for all t > 0,
Lemma 4 (see [30].)Let V(·):[t0 − τ, ∞)→[0, ∞) be a continuous function such that
Lemma 5 (see [31].)Let q ≥ 0, τ > 0, μk > 0 (k = 1,2, …), and p be constants, and assume that V(t) is a piecewise continuous nonnegative function satisfying
3. Main Results
In this section, some sufficient criteria will be given based on the sliding intermittent control scheme. First, the global exponential stability of the closed-loop hybrid neural networks (4) is analyzed, and then several criteria are obtained by setting different parameters in the sliding intermittent controller.
Theorem 6. Assume the upper bound delay τ* < min {θT, (1 − θ)T} and the external imposed impulsive strengths satisfy, . Under the sliding intermittent control, the closed-loop control system (4) is globally exponentially stable if there exist constants β and, such that the following conditions hold:
(i)
(ii)
(iii)
where;;; ρ = max i,j {η − ai, η − bj};;is used to denote the last impulsive moment on the interval [(l + θ)T, (l + 1)T) with; γ = τ*/T; 0 < η ≤ η*;with functions Fi(·), Gj(·) defined as
More specifically, we have the following inequality:
Proof. For the functions Fi(·) and Gj(·) defined in (16), from the condition (13), it is clear that
(1) When, one is easy to have
(2) When t ∈ [(l + θ)T, (l + 1)T) and t ≠ tk, , k ∈ ℕ+, it is easy to have
When t ∈ [(l + θ)T, (l + 1)T) and t = tk,
(3) Now, we are ready to estimate V(t) based on the inequalities (23) and (29) with the method of induction.
-
When t ∈ [0, θT), one obtains
() -
When t ∈ [θT, T), one can derive
() -
When t ∈ [T, (1 + θ)T), we have
() -
When t ∈ [(1 + θ)T, 2T), one can derive
()
By induction, one can derive the following estimation of V(t) for any integer:
-
when t ∈ [lT, (l + θ)T),
() -
and when t ∈ [(l + θ)T, (l + 1)T),
()
By setting γ = τ*/T and substituting it to the above two inequalities, one has, for t ∈ [lT, (l + θ)T),
Remark 7. In the above Theorem 6, the control width θ ∈ (0,1) which does not include the boundary cases. If the parameter θ → 0, the controlled system approximates to impulsive neural networks. If the parameter θ → 1, the controlled system approximates to continuous neural networks. And the controlled system can be handled, respectively, by the methods of the impulsive system and the continuous system. In order to avoid such boundary cases, usually we can take θ = 0.5; that is, the periodically intermittent controller and the impulsive controller play a significant role in the process of control; this results a switched neural networks.
Remark 8. Most of the literatures [28, 32] concerning the global exponential stability of the delayed BAM neural networks with impulses have focused on the stable system. Namely, without the impulsive disturbance, the original neural networks are stable, and under the impulsive disturbance the system can still be kept stable with particular conditions. While, in this article, the impulses can be viewed as either control input or impulsive disturbance, at the same time, the original system is not required to be stable initially.
If adjustable parameter θ = 1, the controlled system turns out to be the following model; that is, the original unstable system (3) is controlled with the continuous feedback controller. Under such case, the conditions in the following proposition will guarantee the closed-loop system to be globally exponentially stable:
Proposition 9. Under the continuous feedback control scheme, the origin of the closed-loop control system (40) is globally exponentially stable if there exist constantsandsuch that
Proof. Consider the Lyapunov function defined as follows:
Lemma 10 (see [23].)Let V(·): [t0 − τ, ∞)→[0, ∞) be a continuous function such that
Proposition 11. Assuming the upper bound delay τ* < min {θT, (1 − θ)T}, under the periodically intermittent control, the closed-loop control system (45) is globally exponentially stable if the control gains andsatisfy the following conditions:
- (i)
()
- (ii)
()
Proof. Considering the same Lyapunov function as that in Theorem 6, by similar analytical technique, one can get the following results on the control period and the control width as follows.
- (1)
When, we have. By Lemma 4, one obtains that, for any t ∈ [lT, (l + θ)T), .
- (2)
When, we have. By Lemma 10, it is derived that, for any t ∈ [(l + θ)T, .
From the above inequality relationships, by similar estimation procedure, we can get the following conclusion:
Proposition 12. Assume the external imposed impulsive strengths. The origin of the closed-loop control system (54) is globally exponentially stable if there exists constant β such that, for k = 1,2, …, the following conditions hold:
Proof. Considering the same Lyapunov function as that in Theorem 6, by similar analytical technique, one can get the following results on the impulsive interval and the impulse moments as follows.
- (1)
When t ∈ (tk−1, tk], the upper right Dini derivative of V(t) along the solution of (54) is depicted as.
- (2)
When t = tk, k ∈ ℕ+,.
From Lemma 5 and the conditions in (55), it follows that
Definition 13 ([21] average impulsive interval). The average impulsive interval of the impulsive sequenceis equal to Ta if there exist positive integer N0 and positive number Ta such that
Lemma 14 (see Lakshmikantham et al., Theorem 1.4.1, [33], [34].)Let PC(ℝ+, ℝ) (PC1(ℝ+, ℝ)) denote the set of piecewise continuous (piecewise continuously differentiable) functions with first kind of discontinuities at tk, k = 1,2, …, from ℝ+ to ℝ. If the following conditions hold,
Lemma 15. Let q ≥ 0, τ > 0, 0 < μ < 1, and p be constants, and assume that V(t) is a piecewise continuous nonnegative function satisfying
Proof. By Lemma 14 and the definition of average impulsive interval, it follows from (63) that, for t ≥ t0,
Next, it is claimed that, for all t > t0,
Supposing (67) is not always true for t > t0, there must exist one time point t* > t0 such that
The following proposition will guarantee the system (59) to be globally exponentially stable.
Proposition 16. Assume the external imposed impulsive strengths, , and the average impulsive interval of the impulsive sequenceis equal to Ta. The impulsive system (59) is globally exponentially stable if the following condition holds:
Proof. Considering the same Lyapunov function as that in Theorem 6, the following results on the impulsive interval and the impulse moments can be obtained.
- (1)
When, the upper right Dini derivative of V(t) along the solutions of (59) is depicted as.
- (2)
When t = tk, k ∈ ℕ+,.
From the above two inequality relationships, and Lemma 15, one has
Remark 17. It should be pointed out that, in the preceding control width of the control period, other kinds of continuous controllers can also be used to achieve the same performance. For example, in [35], the adaptive control scheme has been employed in the control width instead of the continuous state feedback, where the adjusting gains can be designed based on different norms. We can borrow such an idea to the sliding intermittent control design. Moreover, the sliding width parameter can be {θi} rather than the fixed width θ, and the period can be {Ti} rather than constant T. By doing so, we might obtain more general conditions. On the other hand, the phenomena of stochastic nonlinearities are extremely ubiquitous in practical controlled systems [36–39]; hence it is more reasonable to consider neural networks with random nonlinearities, and this will be our future works.
4. Illustrative Example
In this section, we present some examples to illustrate the applicability and efficiency of the proposed control scheme.
Example 1. Considering the following extensively studied BAM neural system,
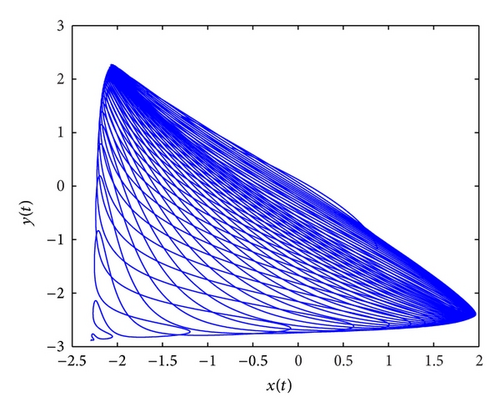
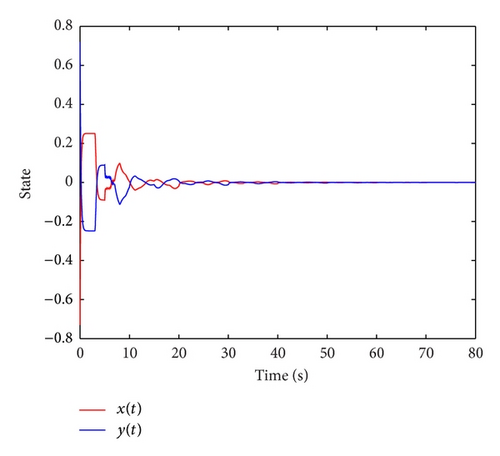
In the following, we will give the convergence results by simulating the system (76). Firstly, by setting the continuous feedback gains k1 = −4.8512, k2 = −4.6378 and the impulsive strengths h1 = h2 = −0.15. With the above parameters setting, calculations show that η* = 0.2679 and μ = 0.85. By setting the control period T = 10, we have control width 0.3 < θ < 0.7 and γ = 0.3. Here we take the parameter θ = 0.5. If we utilize uniform distributed impulsive sequences (tk − tk−1 = 0.01) in the latter control width of the control period, it is easy to check that when η = 0.0221, we have ρ = −1.1410,, and. By choosing β = −4.8519, one has d = 1.1765, ln μ/(tk − tk−1) − β = −11.4000, , λ1 = 0.0565, λ2 = 0.0168, and η + λ1(θ − γ) − λ2(θ + γ) − ln d/T = 0.0037, which means all the conditions in Theorem 6 hold. The simulation result under the sliding intermittent control is given in Figure 3.
Next, the corresponding convergence results under the propositions obtained in this article will be illustrated.
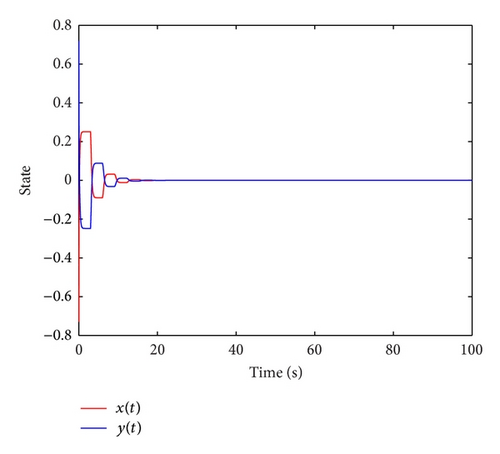
If we utilize the continuous feedback control, by taking the same continuous feedback gains as the above sliding intermittent control, the conditions in Proposition 9 hold, and the simulation result under the continuous feedback control is given in Figure 4.
If we use pure periodically intermittent control, by setting the continuous feedback gains k1 = −6.8512, k2 = −6.6378, we get η* = 0.3682,. It is easy to know when η = 0.0002, we have,, and λ1 = 0.1742. In Proposition 11, by taking T = 100, the relationships among the upper bound delay, the control width, and the control period infer that 0.03 < θ < 0.97, while the last inequality in Proposition 11 means θ > 0.9640. Here we set the θ = 0.9650, and the simulation result under the periodically intermittent control is given in Figure 5.
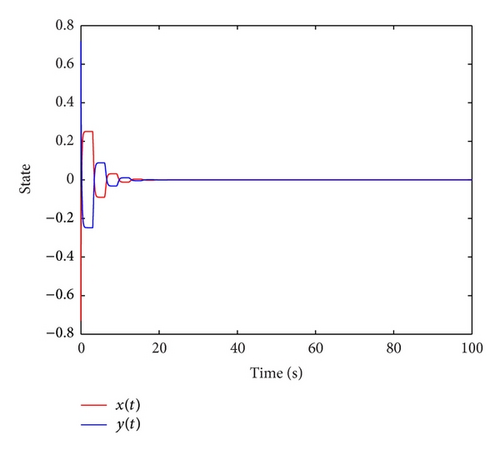
If we use full impulsive control with uniform distributed impulsive sequences (tk − tk−1 = 0.04) and the impulsive strengths μk = 0.85, k = 1,2, …, it is easy to check when β = −3.1262, η = 0.0002, the parameters d = 1.1332, ρ = −1.1629, and , all the conditions in Proposition 12 satisfied. If we use the semi-impulsive control scheme and set the impulsive sequences satisfying the average impulsive interval with Ta = 0.038 and N0 = 1; it is easy to check, which infers that the condition in Proposition 16 holds. The simulation results for system (75) with the full impulsive control and the semi-impulsive control are given in Figures 6 and 7.
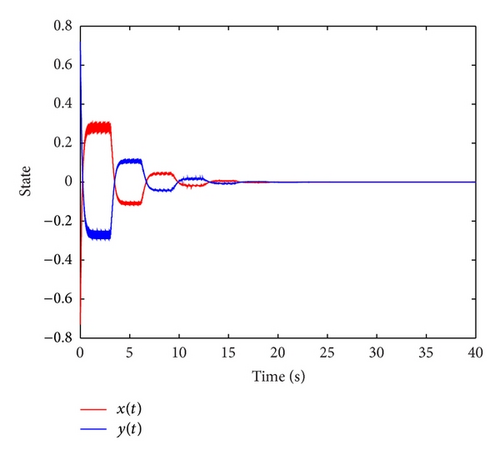
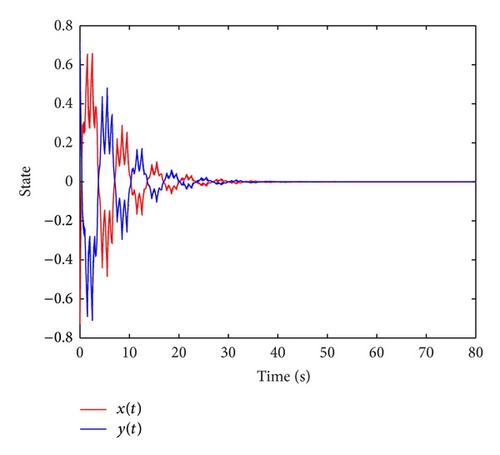
Remark 18. From the above verifying process, it can be found that the sliding intermittent control is much better than the pure periodically intermittent control. More specifically, in the periodically intermittent control, the control period T = 100 and the control width θ = 0.965, while in the sliding intermittent control, the control period T = 10 and the control width θ = 0.5. As for the impulsive control, the full impulsive control is better than the semi-impulsive control in that the earlier converges faster. When dealing with the nonuniformly distributed impulsive sequence, the result derived in Proposition 16 is less conservative.
Example 2. Consider the following unstable delayed BAM neural network, and we will show that the sliding intermittent control benefits the stabilization of the unstable system:
The activations functions f(x) = g(x) = 1/(1 + e−x) − 1/2 with Lf = Lg = 0.25 and the time delays τ = σ = 3. The system has an unstable equilibrium 0 under the above parameters with the initial functions x(t) = [−0.73, −0.79, −0.82] T, y(t) = [0.72,0.87,0.83,0.76] T, t ∈ [−3,0].
In the following, we will check the convergence results for system (77) under the sliding intermittent controller. Setting the continuous feedback gains k(1) = diag {−8.0350, −10.4875, −13.1075}, k(2) = diag {−11.1950, −8.4125, −5.7425, −4.1475}, the impulsive strengths are identical with, i ∈ ℐn, j ∈ ℐm, k ∈ ℕ+, and the control period T = 15; some calculations show that η* = 0.2604, μ = 0.75. We can get the control width 0.2 < θ < 0.8 and γ = 0.2; here we take the parameter θ = 0.4. If we utilize the uniform distributed impulsive sequences (tk − tk−1 = 0.02) in the latter control width of the control period, it is easy to know when η = 0.1250, we have ρ = −2.1433,, and . By choosing β = −4.6841, one has ln μ/(tk − tk−1) − β = −9.7000, d = 1.333,, λ1 = 0.1135, λ2 = 0.1924, and η + λ1(θ − γ) − λ2(θ + γ) − ln d/T = 0.0131, which mean all the conditions in Theorem 6 hold. The simulation result under the sliding intermittent control is given in Figure 8.
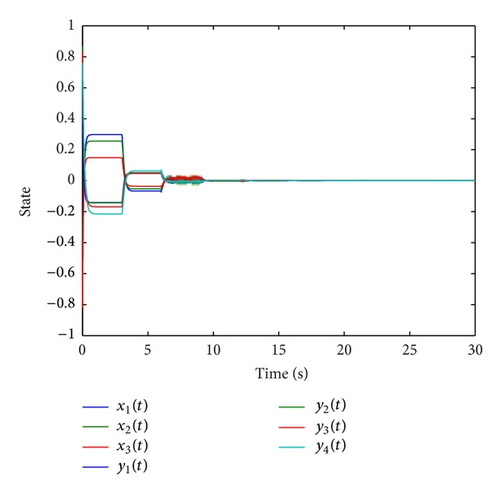
5. Conclusions
In this paper, a sliding intermittent controller has been proposed by unifying the periodically intermittent control with the impulsive control together with continuous feedback control. More specifically, the continuous feedback control is employed as the preceding control width, and the impulsive control is resorted in the latter control width. Furthermore, the adjustable parameter θ ∈ [0,1] is very flexible in that the continuous feedback control (θ = 1), the impulsive control (θ = 0), the periodically intermittent control, and the semi-impulsive control (0 < θ < 1) are all possible cases. Based on the analysis technique and the Lyapunov function approach, the conditions have been constructed for the exponential stability of the delayed BAM neural networks under the proposed control schemes. Finally, numerical simulations are used to illustrate the effectiveness of the control technique.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 61174136, the Natural Science Foundation of Jiangsu Province of China under Grant BK2011598, the Program for New Century Excellent Talents in University under Grant NCET-12-0117, and the Fundamental Research Funds for the Central Universities under Grant 2242012155.




