Size Effects on Magnetic Properties of Ni_0.5Zn_0.5Fe₂O₄ Prepared by Sol-Gel Method

1. Introduction

Spinel ferrites have attracted more and more attention due to their various technological applications in some fields, such as microwave absorption, high-speed digital tape, ferrofluid, magnetic recording, and photomagnetic materials [1–5]. Among the spinel ferrites, nickel zinc ferrite is one of the most versatile magnetic materials as they have high saturation magnetization, high Curie temperature, excellent chemical stability, low coercivity, and biodegradability [6]. It is a mixed spinel structure based on a face-centered cubic lattice of oxygen ions, with functional units of (Zn_xFe_1−x)[Ni_1−xFe_1+x]O₄. Zn²⁺ and Ni²⁺ ions are known to have very strong preferences for the tetrahedral A and octahedral B sites as depicted by curled and square brackets [2], respectively, while Fe³⁺ ions partially occupy the A and B sites. In the case of Zn_1−xNi_xFe₂O₄ ferrite, it was found that for x greater than 0.5, Fe³⁺ moments in A and B sites have collinear arrangement, whereas for x less than 0.5, Fe³⁺ moments in the B site have noncollinear arrangement [7]. The compositional variation can result in the redistribution of metal ions in the A and B sites, which can modify the properties of nickel zinc ferrites. The nickel concentration effect on structure and magnetic of Ni_xZn_1−xFe₂O₄ has been reported [8]. The result showed the superparamagnetic nature of the samples for x = 0.1 and x = 0.3 whereas the material showed ferromagnetic for x = 0.5, but the crystallite size increased unobviously from 12 to 17 nm corresponding x = 0.1 to x = 0.5. Therefore, the nickel concentration played an important role in determining the magnetic properties of Ni_xZn_1−xFe₂O₄. In our previous studies [9], it is found that Ni_0.5Zn_0.5Fe₂O₄ (NZFO) presents the best magnetic and microwave absorption ability in Ni_xZn_1−xFe₂O₄ system. Therefore, it is necessary to further study the magnetic properties of NZFO nanoparticles.

George et al. [10] have studied finite size effects on the structural and magnetic properties of NiFe₂O₄ powders. They found the specific saturation magnetization decreased with decreasing grain size, which may be due to noncollinear magnetic structure and surface effects. The coercivity reached a maximum when the grain size was 15 nm and then decreased as the grain size increased further, which can be explained on the basis of domain structure. Chen and Zhang [11] have reported size effects on magnetic of MgFe₂O₄ spinel ferrite nanocrystallites. The MgFe₂O₄ nanoparticles showed typical superparamagnetism, which unambiguously correlated with the particle size from 6 to 18 nm. However, few groups have investigated size effects on magnetic properties of NZFO ferrite prepared by sol-gel method.

In the present work, the sol-gel method has been used to prepare NZFO with different heat treatment temperatures. To the best of our knowledge, it is the first time to systematically demonstrate size effects of nanocrystallite ferrite on the magnetic behavior. The possible mechanism is discussed here.

2. Experimental

In order to synthesize NZFO, stoichiometric amounts of nickel nitrate, zinc nitrate, and iron nitrate were dissolved in deionized water under heating and magnetic stirring. After stirring for 30 min, citric acid was slowly added to the mixed nitrates solution. The mole ratio of citric acid and total metal ions was controlled to be 1.5 : 1. Urea was added to adjust the pH value to 7. The mixed solution was stirred at 80°C until forming viscous brown gel. Then, the viscous brown gel was placed in the oven at 80°C for 1-2 days to obtain a dry gel. The as-burnt powders were obtained when the dry gel was calcinated at 350°C for 3 h. Finally, the as-burnt powders were annealed in the muffle furnace at different temperatures in the range 400–1100°C in steps of 100°C for 2 h with a heating rate of 5°C/min in air. The as-burnt powders with different annealing temperatures were named as NZFO-350, NZFO-400, NZFO-500, NZFO-600, NZFO-700, NZFO-800, NZFO-900, NZFO-1000, and NZFO-1100, respectively.

Phase analysis of the products was performed by Philips X’pert PRO X-ray diffractometer with Cu K_α radiation. TEM (JEM-2010) was used to show the morphology and particle size distribution. The magnetic properties of the NZFO ferrite powders were measured by using a superconducting quantum interference device magnetometer measurement system (SQUID, MPMS-5T). Zero-field-cooling (ZFC) and field-cooling (FC) magnetization curves were performed in the temperature range between 5 and 350 K under an applied magnetic field of 100 Oe.

3. Results and Discussion

3.1. Structure and Morphology

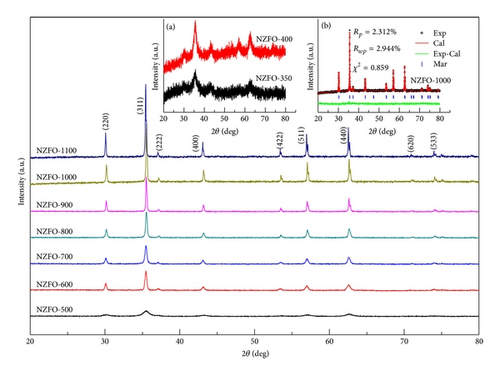
Figure 1 shows XRD patterns samples treated under different annealing temperatures. The XRD patterns have a good agreement with the standard JCPDS cards for nickel zinc ferrite (card no. 08-0234), which confirms single phase cubic spinel structure (space group $$) of ferrite samples. Figure 1(a) shows that the as-burnt sample appears diffraction peak of spinel ferrite, but the crystallinity is still relatively low, with less defined diffraction peaks. Figure 1 shows that the corresponding diffraction peaks become narrower and sharper with increasing annealing temperature, which indicates the growth in crystallite size [12] and much better crystallinity. It is expected that if one introduces annealing temperature in the system much higher, the molecular concentration at the crystal surface will increase and hence the crystal growth will be promoted [13]. In addition, a higher temperature can enhance the atomic mobility and make grains get more energy to grow up.

The lattice constant a for the samples is shown in Table 1. The a value obviously decreases as the annealing temperature increases from 400 to 700°C. The sample calcined at lower temperature is partially crystallization. So, surface defects can occur within the lattice, but the crystallization will enhance with the increase of annealing temperature, which can result in lattice contraction. The a is also observed to increase as the annealing temperature increases from 700 to 800°C but again decrease for samples annealed at above 800°C. This increase and decrease of a could be attributed to redistribution of cations between tetrahedral and octahedral sites and zinc loss from the sample [14], respectively. In addition, the redistribution of cations between tetrahedral and octahedral sites is also supported by the magnetic measurement, as discussed later in this paper. Figure 1(b) shows refinement value of XRD pattern for NZFO-1000. The similarity between the experimental and simulated pattern confirms single phase cubic spinel structure of nanoparticles. The average crystallite size for all NZFO nanoparticles is calculated from intensity (220), (311), (511), and (440) peaks by the Debye-Scherrer equation

$$ ()

where D is the crystallite size, λ is the wavelength of Cu K_α (1.540598 Å), θ is the angle of Bragg diffraction, and β is the full width at half maxima (FWHM) broadening. The obtained crystallite size at different annealing temperature is listed in Table 1. The calculation results show that crystallite size increases from 9 nm to 96 nm with increasing annealing temperature, which may be due to the increasing crystallinity.

Table 1. Structural and magnetic parameters of Ni_0.5Zn_0.5Fe₂O₄ ferrites from 350 to 1100°C.

T (°C)	D (nm)	a (Å)	$$	Ms (μB/f.u.)	Hc (Oe)		Mr (μB/f.u.)
				300 K	300 K	10 K	300 K
350	9	—	—	0.26	0	478	0
400	10	8.3965	—	0.79	3.6	687	0.0017
500	13	8.3922	76.7	1.53	5.6	530	0.0085
600	30	8.3775	13.7	2.03	58.2	114	0.21
700	33	8.3750	13.5	2.77	58.0	—	0.19
800	46	8.3792	10.7	2.87	50.8	117	0.26
900	81	8.3776	1.57	3.12	32.3	—	0.17
1000	88	8.3766	2.15	3.09	25.4	44	0.12
1100	96	8.3774	2.14	3.14	15.1	—	0.06

In addition, the Williamson and Hall (W-H) plots [15] are also used to calculate the crystallite size. The equation is as follows:

$$ ()

where β (FWHM in radian) is measured for different XRD lines corresponding to different planes, θ is the Bragg angle, ε is the strain, and D is the crystallite size. Equation (2) represents a straight line between 4 sin θ (x-axis) and β cos θ (y-axis). The values of ε and D are obtained by the slope (ε) and intercept (λ/D) of line, respectively. The strain rapidly increases for smaller crystallite which can be due to the increasing defect density. The value of ε obviously decreases with increasing annealing temperature (listed in Table 1), which are consistent with those calculated from a values. Figure 2 shows the linear fitting W-H plots of NZFO-500, NZFO-600, NZFO-800, and NZFO-1000. From the parameters of linear fitting, the λ/D values are 0.01528, 0.00475, 0.00432, and 0.00206, respectively, corresponding to NZFO-500, NZFO-600, NZFO-800, and NZFO-1000. Therefore, the calculation D values are 10 nm, 32 nm, 36 nm, and 75 nm, respectively, which are consistent with the previous calculated crystallite size by the Debye-Scherrer equation. So the annealing temperatures play an important role in controlling the crystallite size of the nanocrystallites.

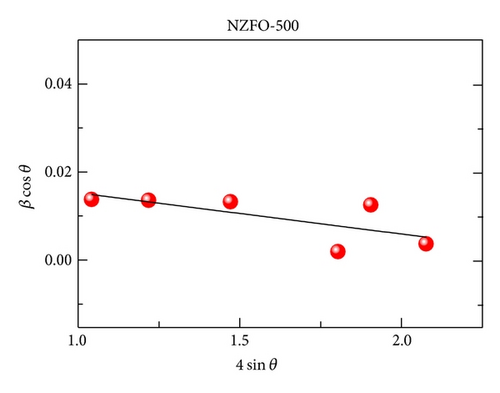
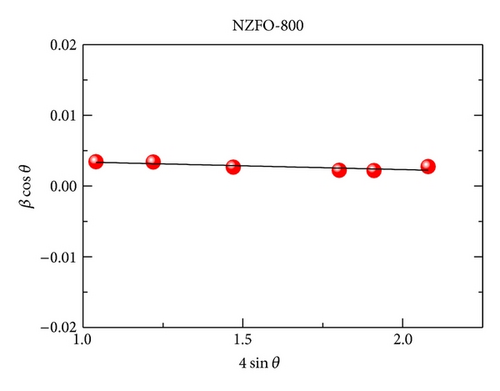
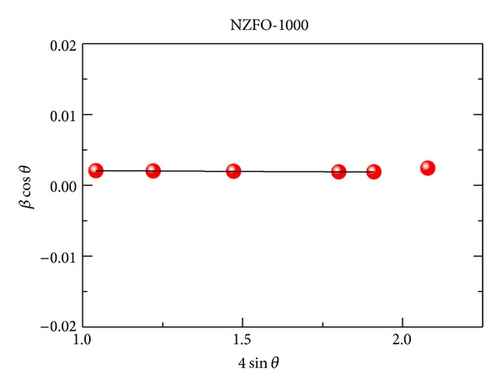
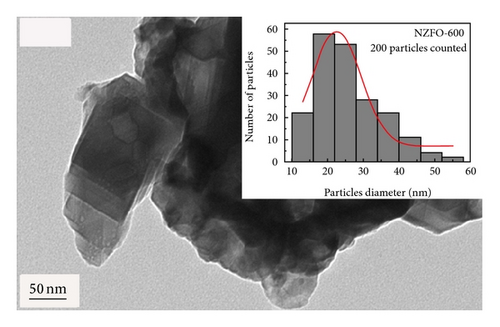
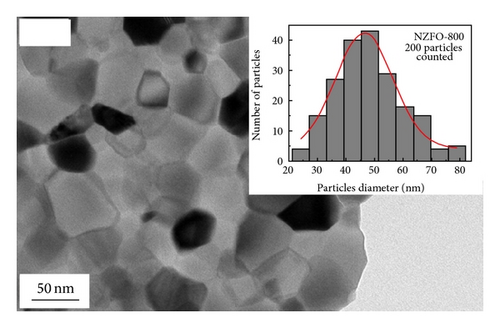
Figure 3 shows the TEM morphology of NZFO-600 and NZFO-800. The particles are similar spherical and polyhedral shapes. For NZFO-800 sample, classical polygonal grain and grain boundary morphologies are present, which shows a higher degree of crystallinity than that of NZFO-600 sample. The insets in Figures 3(a) and 3(c) are particle size distribution graph by counting 200 nanoparticles. The histogram of the size distribution is characterized by a Gaussian function (solid line). It is found that average particle size of NZFO-600 and NZFO-800 is obtained as 23 nm and 46 nm, respectively, which are in agreement with those of the XRD patterns. Therefore, the average crystallite size obtained from XRD analysis is taken as the average particle size. High-resolution TEM (HRTEM) analysis is employed to determine the crystal facets and orientation, as shown in Figures 3(b) and 3(d). In Figure 3(d), two sets of lattices are present and they are oriented at a certain angle with the interfringe spacing of 0.24 nm and 0.25 nm, corresponding to spinel (222) and (311) lattice planes of NZFO-800 ferrite.

3.2. Magnetic Properties

Figure 4 shows the room temperature M-H curves for Ni-Zn ferrites particles with different particle sizes. A similar room temperature M-H curve result was also observed by Jiang et al. [16]. The inset in Figure 4 shows the magnified view of the M-H curves at lower applied field, which shows that hysteresis appears obviously when calcinated at 600°C. In Figure 4, the NZFO-350, NZFO-400, and NZFO-500 samples exhibit nonsaturated magnetization even at the maximum applied field of 10 kOe, and the coercivity (H_c) and the remanent magnetization (M_r) are almost zero, which indicate the superparamagnetic nature. The magnetic moment is obtained using nonlinear curve fit of Langevin function. The function is expressed as [17]

$$ ()

where μ = M_sπD³/6 is the true magnetic moment of each particle, M_s is the saturation magnetization, k_B is the Boltzmann constant, and T is the absolute temperature. The fit results are displayed in Figure 5.

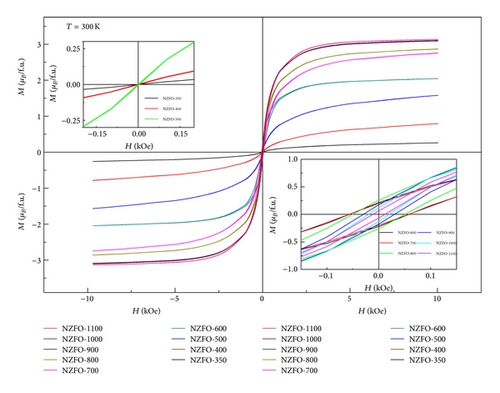
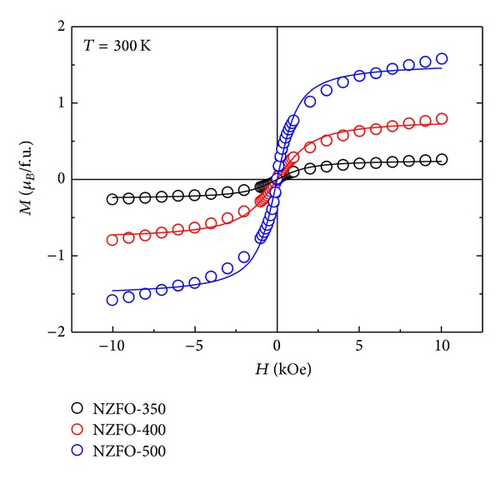
Figure 6 shows M-H loops of the nanoparticles with different particle sizes at 10 K. NZFO nanoparticles show typical hysteresis behaviors. The values of H_c are listed in Table 1.

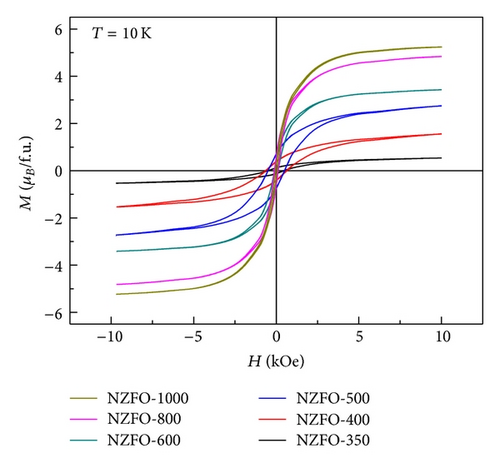
The variation of M_s and H_c with different particle size is shown in Figure 7. The magnetic moment for formula unit in Bohr magneton is calculated and the obtained data are displayed in Table 1. It is seen that M_s decreases as the particle size decreases. Kumar et al. [18] had reported that the existence of spin canting, cation distribution, and disordered surface layer could result in decreased M_s. The surface effects become significant as the particle size decreases, which can lead to the decrease of M_s. Another possible factor is the redistribution of cations between A and B sites, which grows the net magnetic moment. According to Neel’s two sublattice model of ferrimagnetism, $$O₄ configuration has 6 μ_B for formula unit. The value is higher than our M_s value, which confirms cation disorder and redistribution. Sreeja et al. [19] had confirmed an abnormal cation distribution of Ni_0.5Zn_0.5Fe₂O₄ with different annealing temperature by Mössbauer spectroscopic study. At lower sintering temperatures, weaker magnetic superexchange interaction and lattice defects can also lead to the smaller value of M_s [20]. Figure 7 shows that H_c increases rapidly as particle size increases with a maximum value of 58.2 Oe at 600°C (30 nm) and then decreases with further increases in particle size. The same observation of H_c change with particle size in Ni-Zn ferrite was reported in earlier study [16]. From the inset of Figure 7, H_c increases as the particle size increases, reaches a maximum value, and then decreases at 10 K as well as at 300 K. The values of H_c decrease as the temperature of measurement increases. A critical particle size of 10 nm is obtained at 10 K. The critical particle size decreases as the temperature of measurement decreases from 300 K to 10 K. Thus, in Figure 7, the peak value of H_c has shifted to the lower particle size when the temperature decreases from 300 K to 10 K. A similar result had been reported by George et al. [10]. The values of H_c and M_r near to zero for NZFO-350, NZF-400, and NZFO-500 display superparamagnetic nature at 300 K. Generally, the H_c for magnetic nanoparticles is closely related to their particle size. Smaller particle sizes correspond to a lower H_c.

This variation of the H_c with particle size can be explained on the basis of domain structure, critical size, and the surface and interface anisotropy of the crystal. A crystallite will spontaneously break up into a number of domains in order to reduce the large magnetization energy if it is a single domain. The ratio of the energy before and after division into domains varied as $$ [10], where D is the particle size. So, the energy reduces as D decreases, which suggests that the crystallite prefers to remain single domain behavior for quite small D.

In the single domain region, the variation of coercivity as a function of particle size is expressed as [17]

$$ ()

where g and h are constants and D and H_c are particle size and coercivity. Therefore, H_c increases as D increases in below a critical particle size.

In multidomain region, the particle size dependence of the coercivity is expressed as

$$ ()

where a and b are constants and D is particle size. So, the coercivity decreases as particle size increases above a critical particle size. These equations’ analysis results are corresponding to our experimental results.

As a result, it indicates a critical particle size for the transition from single domain to multidomain behavior close to 30 nm at 300 K. In the spherical particle model, the critical size from single domain to multidomain can be calculated with the following formula [21]:

$$ ()

where σ_w = (2k_BT_C|K₁|/a) ^1/2 is the domain wall energy, k_B is Boltzmann constant, T_c is Curie temperature, K₁ is magnetocrystalline anisotropy constant, a is the lattice constant, and M_s is the saturation magnetization. The particle is considered to be single domain below D_m, while the particles are multidomain above D_m. For NZFO, T_c = 538 K, a = 8.39  ×  10⁻⁸ cm, |K₁| = 1.7  ×  10⁴ erg/cm³, and M_s = 310 Gs. From (6), the calculation value of D_m is about 25.9 nm, which is almost consistent with the experimental result (30 nm). So, the average particle size of NZFO-600 is close to the critical size. For D < D_m, these nanocrystallites are single domain, and the surface effect becomes important. In the prepared NZFO powders, the low magnetization value can be attributed to noncollinear surface spins that present in the surface of nanoparticles. As a result, the M_s decreases, which is confirmed by the experimental curve of M_s that decreases more rapidly as the values of D decrease. For D > D_m, the magnetic domain structure appears. Compared with the single domain, multidomain particles require fewer magnetic fields to switch for domain wall motion, which improves saturation magnetization [22]. Moreover, the surface effects become weak for larger particle size and the sample reaches the saturation of bulk ferrite. Thus, the experimental curve of M_s versus D in Figure 7 is almost horizontal for higher value of D. This can also be due to the low strain value. So, the effects of strain on the magnetic of NZFO-900, NZFO-1000 and NZFO-1100 can be ignored.

Figure 8 shows the variation of magnetization with temperature (5 K < T < 350 K) curves in an external field of 100 Oe recorded in ZFC and FC modes. The ZFC-FC curves separation at lower temperature can be speculated as a high field irreversibility (M_FC > M_ZFC) behavior below a certain temperature, irreversibility temperature, T_irr. The irreversibility behavior also indicates that there is a nonequilibrium magnetization state. The difference between M_ZFC and M_FC values become much larger at a certain temperature with increasing particle size for all examples, which may have some reasons as follows. M_FC and M_ZFC of different magnetic systems are found to be related through the expression [23]

$$ ()

$$ ()

where H_app and H_c are the applied field and coercivity, respectively. Here, H_app = 100 Oe, and H_c varies with particle size. M_ZFC value is calculated by using the previous expression from the measured M_FC at different annealing temperatures. For example, according to (7), the value of M_ZFC and M_FC will be almost identical at 300 K because H_app = 100 Oe compared to H_c = 3.6 Oe for NZFO-400, which can be further proven ZFC and FC curve shapes of Figures 8(a), 8(b), and 8(c).

The ZFC magnetization curves appear maximum at the blocking temperature T_B at which the relaxation time equals the time scale of the magnetization measurements. From Figures 8(a), 8(b), and 8(c) curves, the ZFC and FC are almost overlapped above T_B, indicating the presence of the small-sized particles [24]. The T_B value of NZFO-350, NZFO-400, NZFO-500 are 121 K, 123 K, and 208 K, respectively, indicating that the different particle size is characterized by different average energy barrier. Note also that the measured T_B value of NZFO above annealing temperature of 600°C is higher than 350 K, as shown Figure 8(d). The obtained M-T curves of NZFO above annealing temperature of 600°C are similar, so only the M-T curves of NZFO-800 is shown. According to the Stoner-Wohlfarth theory, the magnetocrystalline anisotropy E_A of a single domain particle can be approximated as follows [25]:

$$ ()

where K is the magnetocrystalline anisotropy constant, V is the volume of the nanoparticle, and θ is the angle between the magnetic direction and the easy axis of the nanoparticle. When E_A is comparable with thermal activation energy, k_BT with k_B as the Boltzmann constant, the magnetization direction of the nanoparticle starts to fluctuate and goes through rapid superparamagnetic relaxation. The T_B is the threshold point of thermal activation. Above T_B, thermal activation can overcome the anisotropy energy barrier and the nanoparticles become superparamagnetic with the magnetization direction randomly flipping. Therefore, a variation of magnetization with applied field at 300 K (T > T_B) is shown in Figure 4, the particles have adequate thermal energy k_BT to attain complete thermal equilibrium with the applied field during the measurement time, and, hence, hysteresis disappears. In single domain, larger particles possess a higher E_A and require a larger k_BT to become superparamagnetic. Therefore, T_B increases as particle size increases. Below T_B, the thermal energy is no longer able to overcome the magnetization anisotropy energy barrier, remanent magnetization and coercivity appear and then exhibit a hysteretic feature, just as shown in Figure 6. According to previous analysis, all the analysis results of ZFC and FC curves are in agreement with magnetization curves.

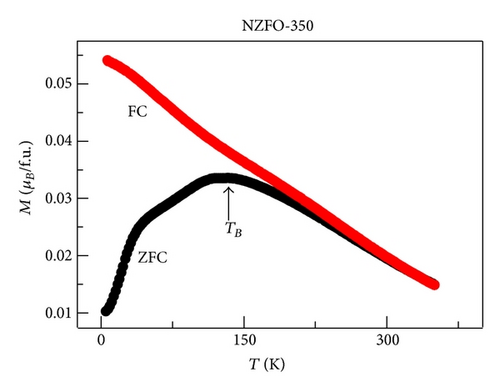
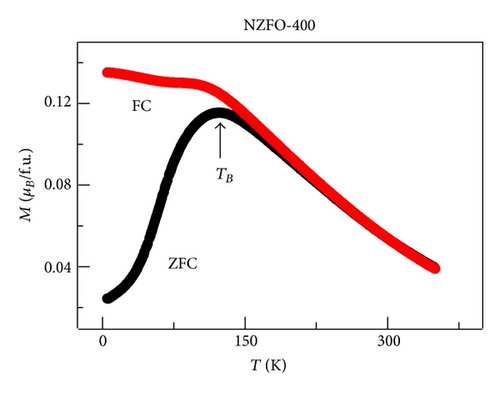
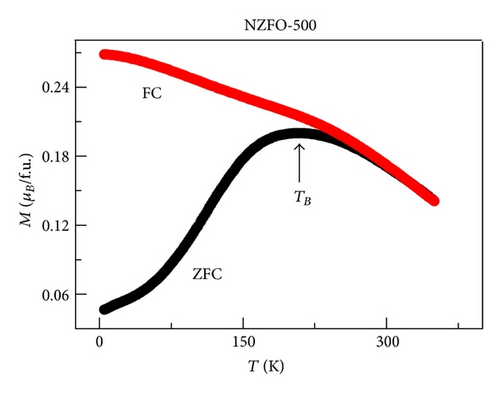
4. Conclusion

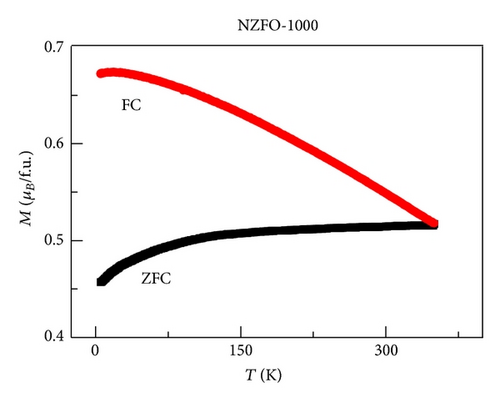
XRD analysis reveals that all samples are the single phase cubic spinel structure, and higher annealing temperature could lead to lattice shrinkage and grain growth. The strain is also induced during the annealing process. The particle size from TEM morphology is in close agreement with the crystallite size by W-H plots. The room magnetic measurement shows superparamagnetic nature for NZFO-350, NZFO-400, and NZFO-500 ferrites, and others show ferrimagnetic nature. The room temperature saturation magnetization increases as particle size increases, with a maximum value of 3.14 μ_B/f.u. corresponding the particle size of 96 nm. The coercivity increases with increasing particle size and reaches a maximum when the particle size reaches a critical size and then decreases as the particle size increases further. This is due to the transition from single domain to multidomain structure. ZFC and FC magnetization behaviors confirm systematically the effect of surface effects on magnetic behavior.