Volume 2013, Issue 1 608943

Research Article

Open Access

An Efficient Approach for Fractional Harry Dym Equation by Using Sumudu Transform

Devendra Kumar,

Devendra Kumar

Department of Mathematics, JaganNath Gupta Institute of Engineering and Technology, Jaipur, Rajasthan 302022, India

Search for more papers by this author

Jagdev Singh,

Jagdev Singh

orcid.org/0000-0001-6853-4138

Department of Mathematics, JaganNath University, Village-Rampura, Tehsil-Chaksu, Jaipur, Rajasthan 303901, India jagannathuniversity.org

Search for more papers by this author

A. Kılıçman,

Corresponding Author

A. Kılıçman

[email protected]

Department of Mathematics and Institute for Mathematical Research, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

Devendra Kumar,

Devendra Kumar

Department of Mathematics, JaganNath Gupta Institute of Engineering and Technology, Jaipur, Rajasthan 302022, India

Search for more papers by this author

Jagdev Singh,

Jagdev Singh

orcid.org/0000-0001-6853-4138

Department of Mathematics, JaganNath University, Village-Rampura, Tehsil-Chaksu, Jaipur, Rajasthan 303901, India jagannathuniversity.org

Search for more papers by this author

A. Kılıçman,

Corresponding Author

A. Kılıçman

[email protected]

Department of Mathematics and Institute for Mathematical Research, Universiti Putra Malaysia, 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author

First published: 22 May 2013

https://doi.org/10.1155/2013/608943

Citations: 27

Academic Editor: Mustafa Bayram

Share a link

Email
Wechat
Bluesky

Abstract

An efficient approach based on homotopy perturbation method by using sumudu transform is proposed to solve nonlinear fractional Harry Dym equation. This method is called homotopy perturbation sumudu transform (HPSTM). Furthermore, the same problem is solved by Adomian decomposition method (ADM). The results obtained by the two methods are in agreement, and, hence, this technique may be considered an alternative and efficient method for finding approximate solutions of both linear and nonlinear fractional differential equations. The HPSTM is a combined form of sumudu transform, homotopy perturbation method, and He’s polynomials. The nonlinear terms can be easily handled by the use of He’s polynomials. The numerical solutions obtained by the HPSTM show that the approach is easy to implement and computationally very attractive.

1. Introduction

Fractional differential equations have gained importance and popularity, mainly due to its demonstrated applications in science and engineering. For example, these equations are increasingly used to model problems in fluid mechanics, acoustics, biology, electromagnetism, diffusion, signal processing, and many other physical processes. The most important advantage of using fractional differential equations in these and other applications is their nonlocal property. It is well known that the integer order differential operator is a local operator but the fractional order differential operator is nonlocal. This means that the next state of a system depends not only upon its current state but also upon all of its historical states. This is more realistic and it is one reason why fractional calculus has become more and more popular [1–9].

In this paper, we consider the following nonlinear time-fractional Harry Dym equation of the form

()

with the initial condition

()

where α is parameter describing the order of the fractional derivative and U(x, t) is a function of x and t. The fractional derivative is understood in the Caputo sense. The general response expression contains a parameter describing the order of the fractional derivative that can be varied to obtain various responses. In the case of α = 1, the fractional Harry Dym equation reduces to the classical nonlinear Harry Dym equation. The exact solution of the Harry Dym equation is given by [10]

()

where a and b are suitable constants. The Harry Dym is an important dynamical equation which finds applications in several physical systems. The Harry Dym equation first appeared in Kruskal and Moser [11] and is attributed in an unpublished paper by Harry Dym in 1973-1974. It represents a system in which dispersion and nonlinearity are coupled together. Harry Dym is a completely integrable nonlinear evolution equation. The Harry Dym equation is very interesting because it obeys an infinite number of conversion laws; it does not posses, the Painleve property. The Harry Dym equation has strong links to the Korteweg-de Vries equation, and applications of this equation were found to the problems of hydrodynamics [12]. The Lax pair of the Harry Dym equation is associated with the Sturm-Liouville operator. The Liouville transformation transforms this operator spectrally into the Schrödinger operator [13]. Recently, a fractional model of Harry Dym equation was studied by Kumar et al. [14], and approximate analytical solution was obtained by using homotopy perturbation method (HPM).

In the present paper, the homotopy perturbation sumudu transform method (HPSTM) basically illustrates how the sumudu transform can be used to approximate the solutions of the linear and nonlinear fractional differential equations by manipulating the homotopy perturbation method. The homotopy perturbation method (HPM) was first introduced and developed by He [15–17]. The HPM was also studied by many authors to handle linear and nonlinear equations arising in various scientific and technological fields [18–24]. The homotopy perturbation sumudu transform method (HPSTM) is a combination of sumudu transform method, HPM, and He’s polynomials and is mainly due to Ghorbani [25, 26]. In recent years, many authors have paid attention to study the solutions of linear and nonlinear partial differential equations by using various methods combined with the Laplace transform [27–30] and sumudu transform [31, 32].

In this paper, we apply the homotopy perturbation sumudu transform method (HPSTM) and Adomian decomposition method (ADM) to solve the nonlinear time-fractional Harry Dym equation. The objective of the present paper is to extend the application of the HPSTM to obtain analytic and approximate solutions to the nonlinear time-fractional Harry Dym equation. The advantage of the HPSTM is its capability of combining two powerful methods for obtaining exact and approximate analytical solutions for nonlinear equations. It provides the solutions in terms of convergent series with easily computable components in a direct way without using linearization, perturbation, or restrictive assumptions. It is worth mentioning that the HPSTM is capable of reducing the volume of the computational work as compared to the classical methods while still maintaining the high accuracy of the numerical result; the size reduction amounts to an improvement of the performance of the approach.

2. Sumudu Transform

In early 1990s, Watugala [33] introduced a new integral transform, named the sumudu transform and applied it to the solution of ordinary differential equation in control engineering problems. The sumudu transform is defined over the set of functions

()

by the following formula:

()

Some of the properties were established by Weerakoon in [34, 35]. Furthermore, fundamental properties of this transform were also established by Asiru [36]. This transform was applied to the one-dimensional neutron transport equation in [37] by Kadem. In fact it was shown that there is strong relationship between sumudu and other integral transform methods; see Kılıçman et al. [38]. In particular the relation between sumudu transform and Laplace transforms was proved in Kılıçman and Gadain [39]. Next, in Eltayeb et al. [40], the sumudu transform was extended to the distributions and some of their properties were also studied in Kılıçman and Eltayeb [41]. Recently, this transform is applied to solve the system of differential equations; see Kılıçman et al. [42]. Note that a very interesting fact about sumudu transform is that the original function and its sumudu transform have the same Taylor coefficients except for the factor n; see Zhang [43]. Thus, if

, then

; see Kılıçman et al. [38]. Similarly, the sumudu transform sends combinations, C(m, n), into permutations, P(m, n), and, hence, it will be useful in the discrete systems.

3. Basic Definitions of Fractional Calculus

In this section, we mention the following basic definitions of fractional calculus.

Definition 1. The Riemann-Liouville fractional integral operator of order α > 0, of a function f(t) ∈ C_μ, μ ≥ −1, is defined as [3]

()

For the Riemann-Liouville fractional integral, we have

()

Definition 2. The fractional derivative of f(t) in the Caputo sense is defined as [6]

()

for m − 1 < α ≤ m, m ∈ N, t > 0.

For the Riemann-Liouville fractional integral and the Caputo fractional derivative, we have the following relation:

()

Definition 3. The sumudu transform of the Caputo fractional derivative is defined as follows [44]:

()

4. Solution by Homotopy Perturbation Sumudu Transform Method (HPSTM)

4.1. Basic Idea of HPSTM

To illustrate the basic idea of this method, we consider a general fractional nonlinear nonhomogeneous partial differential equation with the initial condition of the form

()

where

is the Caputo fractional derivative of the function U(x, t), R is the linear differential operator, N represents the general nonlinear differential operator and g(x, t) is the source term.

Applying the sumudu transform (denoted in this paper by S) on both sides of (11), we get

()

Using the property of the sumudu transform, we have

()

Operating with the sumudu inverse on both sides of (14) gives

()

where G(x, t) represents the term arising from the source term and the prescribed initial conditions. Now we apply the HPM

()

and the nonlinear term can be decomposed as

()

for some He′s polynomials H_n(U) [26, 45] that are given by

()

Substituting (16) and (17) in (15), we get

()

which is the coupling of the sumudu transform and the HPM using He′s polynomials. Comparing the coefficients of like powers of p, the following approximations are obtained:

()

Proceeding in this same manner, the rest of the components U_n(x, t) can be completely obtained and the series solution is thus entirely determined. Finally, we approximate the analytical solution U(x, t) by truncated series

()

The previous series solutions generally converge very rapidly. A classical approach of convergence of this type of series is already presented by Abbaoui and Cherruault [46].

4.2. Solution of the Problem

Consider the following nonlinear time-fractional Harry Dym equation:

()

with the initial condition

()

Applying the sumudu transform on both sides of (22), subject to initial condition (23), we have

()

The inverse Sumudu transform implies that

()

Now applying the HPM, we get

()

where H_n(U) are He’s polynomials that represent the nonlinear terms. So, the He’s polynomials are given by

()

The first few components of He’s polynomials are given by

()

Comparing the coefficients of like powers of p, we have

()

In this manner the rest of components of the HPSTM solution can be obtained. Thus, the solution U(x, t) of the (22) is given as

()

The series solution converges very rapidly. The rapid convergence means that only few terms are required to get analytic function. Now, we calculate numerical results of the approximate solution U(x, t) for different values of α = 1/3,1/2,1 and for various values of t and x. The numerical results for the approximate solution obtained by using HPSTM and the exact solution given by Mokhtari [10] for constant values of a = 4 and b = 1 for various values of t, x, and α are shown in Figures 1(a)–1(d), and those for different values of x and α at t = 1 are depicted in Figure 2. It is observed from Figures 1(a)–1(c) that U(x, t) decreases with the increase in both x and t for α = 1/3,1/2, and α = 1. Figures 1(c)-1(d) clearly shows that, when α = 1, the approximate solution obtained by the HPSTM is very near to the exact solution. It is also seen from Figure 2 that as the value of α increases, the displacement U(x, t) increases. It is to be noted that only the third order term of the HPSTM was used in evaluating the approximate solutions for Figure 1. It is evident that the efficiency of the present method can be dramatically enhanced by computing further terms of U(x, t) when the HPSTM is used.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The behaviour of the U(x, t) with respect to x and t being obtained, with (a) α = 1/3; (b) α = 1/2; (c) α = 1; (d) exact solution.

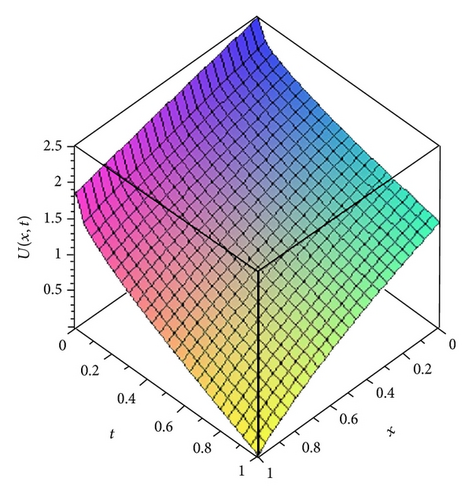
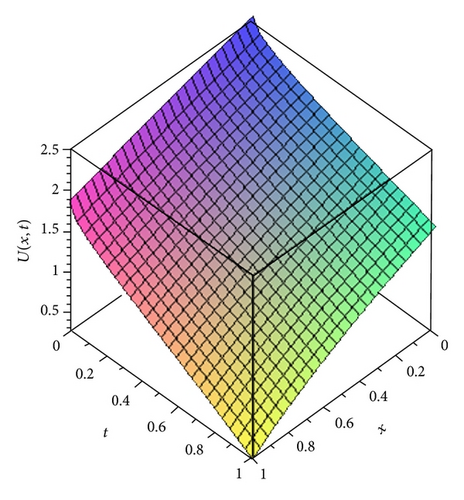
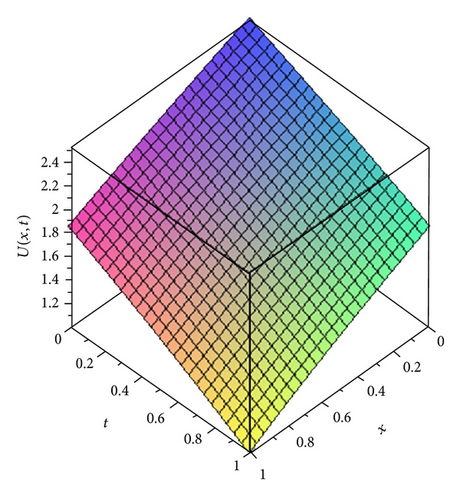
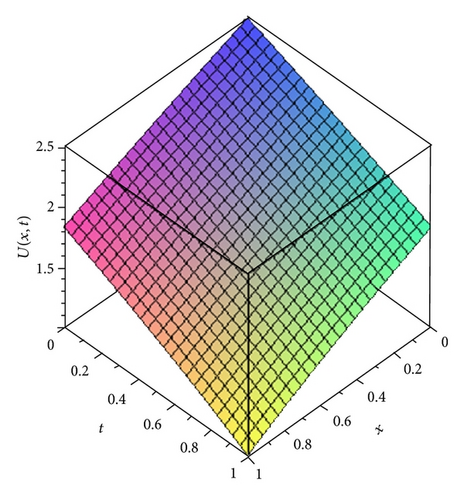
5. Solution by Adomian Decomposition Method (ADM)

5.1. Basic Idea of ADM

To illustrate the basic idea of Adomian decomposition method [47, 48], we consider a general fractional nonlinear nonhomogeneous partial differential equation with the initial condition of the form

()

where

is the Caputo fractional derivative of the function U(x, t), R is the linear differential operator, N represents the general nonlinear differential operator, and g(x, t) is the source term.

Applying the operator

on both sides of (31) and using result (9), we have

()

Next, we decompose the unknown function U(x, t) into sum of an infinite number of components given by the decomposition series

()

and the nonlinear term can be decomposed as

()

where A_n are Adomian polynomials that are given by

()

The components U₀, U₁, U₂, … are determined recursively by substituting (33) and (34) into (32) leading to

()

This can be written as

()

Adomian method uses the formal recursive relations as

()

5.2. Solution of the Problem

To solve the nonlinear time-fractional Harry Dym equation (22)-(23), we apply the operator

on both sides of (22) and use result (9) to obtain

()

This gives the following recursive relations using (38):

()

where

()

The first few components of Adomian polynomials are given by

()

The components of the solution can be easily found by using the previous recursive relations as

()

and so on. In this manner the rest of components of the decomposition solution can be obtained. Thus, the ADM solution U(x, t) of (22) is given as

()

which is the same solution as obtained by using HPSTM.

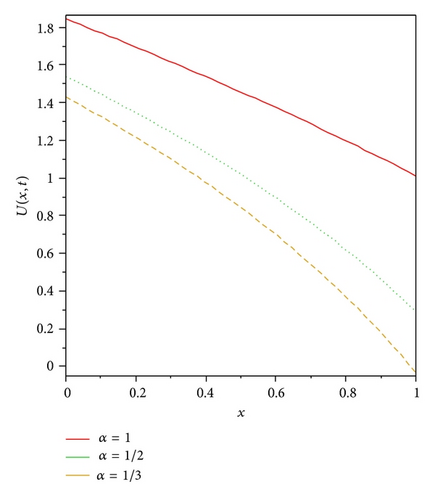
From Table 1, it is observed that the values of the approximate solution at different grid points obtained by the HPSTM and ADM are close to the values of the exact solution with high accuracy at the third term approximation. It can also be noted that the accuracy increases as the order of approximation increases.

Table 1. Comparison study between HPSTM, ADM, and the exact solution, when α = 1 and for constant values of a = 4 and b = 1.

x	t	HPSTM	ADM	Exact solution
0	1	1.843946953	1.843946953	1.843946953
0.2	1	1.694117377	1.694117377	1.691538112
0.4	1	1.537581542	1.537581542	1.534036644
0.6	1	1.373028020	1.373028020	1.367980757
0.8	1	1.198654865	1.198654865	1.191138425
1.0	1	1.011880649	1.011880649	1.000000000

6. Conclusions

In this paper, the homotopy perturbation sumudu transform method (HPSTM) and the Adomian decomposition method (ADM) are successfully applied for solving nonlinear time-fractional Harry Dym equation. The comparison between the third order terms solution of the HPSTM, ADM, and exact solution is given in Table 1. It is observed that for t = 1 and α = 1, there is a good agreement between the HPSTM, ADM, and exact solution. Therefore, these two methods are very powerful and efficient techniques for solving different kinds of linear and nonlinear fractional differential equations arising in different fields of science and engineering. However, HPSTM has an advantage over the Adomian decomposition method (ADM) such that it solves the nonlinear problems without using Adomian polynomials. In conclusion, the HPSTM may be considered as a nice refinement in existing numerical techniques and might find wide applications.

Acknowledgments

The authors are very grateful to the referees for their valuable suggestions and comments for the improvement of the paper. The third author also gratefully acknowledges that this research was partially supported by the University Putra Malaysia under the Research Universiti Grant Scheme 05-01-09-0720RU and the Fundamental Research Grant Scheme 01-11-09-723FR.

References

1 Young G. O., Definition of physical consistent damping laws with fractional derivatives, Zeitschrift für Angewandte Mathematik und Mechanik. (1995) 75, 623–635.
10.1002/zamm.19950750820
Web of Science® Google Scholar
2 R. Hilfer, Applications of Fractional Calculus in Physics, 2000, World Scientific, Singapore.
10.1142/3779
Google Scholar
3 Podlubny I., Fractional Differential Equations, 1999, Academic Press, New York, NY, USA.
Web of Science® Google Scholar
4 Mainardi F., Luchko Y., and Pagnini G., The fundamental solution of the space-time fractional diffusion equation, Fractional Calculus and Applied Analysis. (2001) 4, 153–192.
Google Scholar
5 Debnath L., Fractional integrals and fractional differential equations in fluid mechanics, Fractional Calculus and Applied Analysis. (2003) 6, 119–155.
Google Scholar
6 Caputo M., Elasticita e Dissipazione, 1969, Zani-Chelli, Bologna, Italy.
Google Scholar
7 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, Wiley, New York, NY, USA.
Google Scholar
8 Oldham K. B. and Spanier J., The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order, 1974, Academic Press, New York, NY, USA.
Google Scholar
9 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, Elsevier, Amsterdam, The Netherlands.
10.1016/S0304-0208(06)80001-0
Google Scholar
10 Mokhtari R., Exact solutions of the Harry-Dym equation, Communications in Theoretical Physics. (2011) 55, no. 2, 204–208, 2-s2.0-79951759802, https://doi.org/10.1088/0253-6102/55/2/03.
10.1088/0253-6102/55/2/03
Web of Science® Google Scholar
11 Kruskal M. D. and Moser J., Dynamical Systems, Theory and Applications, 1975, Springer, Berlin, Germany, Lecturer Notes Physics.
Google Scholar
12 Vasconcelos G. L. and Kadanoff L. P., Stationary solutions for the Saffman-Taylor problem with surface tension, Physical Review A. (1991) 44, no. 10, 6490–6495, 2-s2.0-0000441867, https://doi.org/10.1103/PhysRevA.44.6490.
10.1103/PhysRevA.44.6490
CAS PubMed Web of Science® Google Scholar
13 Gesztesy F. and Unterkofler K., Isospectral deformations for Strum-Liouville and Dirac-type operators and associated nonlinear evolution equations, Reports on Mathematical Physics. (1992) 31, no. 2, 113–137, 2-s2.0-0012274610.
10.1016/0034-4877(92)90008-O
Google Scholar
14 Kumar S., Tripathi M. P., and Singh O. P., A fractional model of Harry Dym equation and its approximate solution, Ain Shams Engineering Journal. (2013) 4, no. 1, 111–115.
10.1016/j.asej.2012.07.001
PubMed Web of Science® Google Scholar
15 He J. H., Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering. (1999) 178, no. 3-4, 257–262, 2-s2.0-0032672778, ZBL0956.70017.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
16 He J. H., Homotopy perturbation method: a new nonlinear analytical technique, Applied Mathematics and Computation. (2003) 135, no. 1, 73–79, ZBL1030.34013, 2-s2.0-0037440579, https://doi.org/10.1016/S0096-3003(01)00312-5.
10.1016/S0096-3003(01)00312-5
Web of Science® Google Scholar
17 He J. H., Asymptotic methods for solitary solutions and compactions, Abstract and Applied Analysis. (2012) 2012, 130, 916793, https://doi.org/10.1155/2013/916793.
10.1155/2012/916793
Google Scholar
18 Ganji D. D., The applications of He’s homotopy perturbation method to nonlinear equation arising in heat transfer, Physics Letters A. (2006) 335, 337–341.
10.1016/j.physleta.2006.02.056
Google Scholar
19 Ganji D. D. and Rafei M., Solitary wave solutions for a generalized Hirota-Satsuma coupled KdV equation by homotopy perturbation method, Physics Letters A. (2006) 356, no. 2, 131–137, ZBL1160.35517, 2-s2.0-33745244211, https://doi.org/10.1016/j.physleta.2006.03.039.
10.1016/j.physleta.2006.03.039
CAS Web of Science® Google Scholar
20 Yildirim A., An algorithm for solving the fractional nonlinear Schrödinger equation by means of the homotopy perturbation method, International Journal of Nonlinear Sciences and Numerical Simulation. (2009) 10, no. 4, 445–450, 2-s2.0-67249166170.
10.1515/IJNSNS.2009.10.4.445
CAS Web of Science® Google Scholar
21 Sweilam N. H. and Khader M. M., Exact solutions of some coupled nonlinear partial differential equations using the homotopy perturbation method, Computers and Mathematics with Applications. (2009) 58, no. 11-12, 2134–2141, ZBL1189.65259, 2-s2.0-70350574745, https://doi.org/10.1016/j.camwa.2009.03.059.
10.1016/j.camwa.2009.03.059
Web of Science® Google Scholar
22 Rashidi M. M., Ganji D. D., and Dinarvand S., Explicit analytical solutions of the generalized burger and burger-fisher equations by homotopy perturbation method, Numerical Methods for Partial Differential Equations. (2009) 25, no. 2, 409–417, 2-s2.0-63449135805, https://doi.org/10.1002/num.20350.
10.1002/num.20350
Web of Science® Google Scholar
23 Yildirim A., He′s homotopy perturbation method for nonlinear differential-difference equations, International Journal of Computer Mathematics. (2010) 87, no. 5, 992–996, ZBL1192.65102, 2-s2.0-77952576056, https://doi.org/10.1080/00207160802247646.
10.1080/00207160802247646
Web of Science® Google Scholar
24 Jafari H., Wazwaz A. M., and Khalique C. M., Homotopy perturbation and variational iteration methods for solving fuzzy differential equations, Communications in Fractional Calculus. (2012) 3, no. 1, 38–48.
Google Scholar
25 Ghorbani A. and Saberi-Nadjafi J., He′s homotopy perturbation method for calculating adomian polynomials, International Journal of Nonlinear Sciences and Numerical Simulation. (2007) 8, no. 2, 229–232, 2-s2.0-34249865652.
10.1515/IJNSNS.2007.8.2.229
Web of Science® Google Scholar
26 Ghorbani A., Beyond Adomian polynomials: he polynomials, Chaos, Solitons and Fractals. (2009) 39, no. 3, 1486–1492, ZBL1197.65061, 2-s2.0-62949242120, https://doi.org/10.1016/j.chaos.2007.06.034.
10.1016/j.chaos.2007.06.034
Web of Science® Google Scholar
27 Khuri S. A., A Laplace decomposition algorithm applied to a class of nonlinear differential equations, Journal of Applied Mathematics. (2001) 1, no. 4, 141–155, 2-s2.0-33744989624, https://doi.org/10.1155/S1110757X01000183.
10.1155/S1110757X01000183
Google Scholar
28 Khan M. and Hussain M., Application of Laplace decomposition method on semi-infinite domain, Numerical Algorithms. (2011) 56, no. 2, 211–218, 2-s2.0-78651520457, https://doi.org/10.1007/s11075-010-9382-0.
10.1007/s11075-010-9382-0
Web of Science® Google Scholar
29 Khan M., Gondal M. A., and Kumar S., A new analytical solution procedure for nonlinear integral equations, Mathematical and Computer Modelling. (2012) 55, 1892–1897, ZBL1255.45003.
10.1016/j.mcm.2011.11.044
Web of Science® Google Scholar
30 Gondal M. A. and Khan M., Homotopy perturbation method for nonlinear exponential boundary layer equation using Laplace transformation, He′s polynomials and pade technology, International Journal of Nonlinear Sciences and Numerical Simulation. (2010) 11, no. 12, 1145–1153, 2-s2.0-79951685762.
Web of Science® Google Scholar
31 Singh J., Kumar D., and Sushila, Homotopy perturbation sumudu transform method for nonlinear equations, Advances in Theoretical and Applied Mechanics. (2011) 4, 165–175, ZBL1247.76062.
Google Scholar
32 Kumar D., Singh J., and Rathore S., Sumudu decomposition method for nonlinear equations, International Mathematical Forum. (2012) 7, no. 11, 515–521, ZBL1250.65126.
Google Scholar
33 Watugala G. K., Sumudu transform—a new integral transform to solve differential equations and control engineering problems, Mathematical Engineering in Industry. (1998) 6, no. 4, 319–329, 2-s2.0-0031654471.
Google Scholar
34 Weerakoon S., Applications of sumudu transform to partial differential equations, International Journal of Mathematical Education in Science and Technology. (1994) 25, no. 2, 277–283.
10.1080/0020739940250214
Google Scholar
35 Weerakoon S., Complex inversion formula for sumudu transforms, International Journal of Mathematical Education in Science and Technology. (1998) 29, no. 4, 618–621.
Google Scholar
36 Asiru M. A., Further properties of the sumudu transform and its applications, International Journal of Mathematical Education in Science and Technology. (2002) 33, no. 3, 441–449, ZBL1013.44001.
10.1080/002073902760047940
Google Scholar
37 Kadem A., Solving the one-dimensional neutron transport equation using Chebyshev polynomials and the sumudu transform, Analele Universitatii din Oradea. (2005) 12, 153–171, ZBL1164.82331.
Google Scholar
38 Kılıçman A., Eltayeb H., and Atan K. A. M., A note on the comparison between laplace and sumudu transforms, Bulletin of the Iranian Mathematical Society. (2011) 37, no. 1, 131–141, ZBL1242.44001, 2-s2.0-79959493170.
Web of Science® Google Scholar
39 Kılıçman A. and Gadain H. E., On the applications of Laplace and Sumudu transforms, Journal of the Franklin Institute. (2010) 347, no. 5, 848–862, 2-s2.0-77955228730, https://doi.org/10.1016/j.jfranklin.2010.03.008.
10.1016/j.jfranklin.2010.03.008
Web of Science® Google Scholar
40 Eltayeb H., Kılıçman A., and Fisher B., A new integral transform and associated distributions, Integral Transforms and Special Functions. (2010) 21, no. 5, 367–379, ZBL1191.35017, 2-s2.0-77951247970, https://doi.org/10.1080/10652460903335061.
10.1080/10652460903335061
Web of Science® Google Scholar
41 Kılıçman A. and Eltayeb H., A note on integral transforms and partial differential equations, Applied Mathematical Sciences. (2010) 4, no. 1–4, 109–118, 2-s2.0-77951103745.
Google Scholar
42 Kılıçman A., Eltayeb H., and Agarwal R. P., On sumudu transform and system of differential equations, Abstract and Applied Analysis. (2010) 2010, 11, 2-s2.0-77952568902, https://doi.org/10.1155/2010/598702, 598702.
10.1155/2010/598702
Google Scholar
43 Zhang J., A sumudu based algorithm for solving differential equations, Computer Science Journal of Moldova. (2007) 15, 303–313.
Google Scholar
44 Chaurasia V. B. L. and Singh J., Application of sumudu transform in schödinger equation occurring in quantum mechanics, Applied Mathematical Sciences. (2010) 4, no. 57–60, 2843–2850, 2-s2.0-78650298757.
Google Scholar
45 Mohyud-Din S. T., Noor M. A., and Noor K. I., Traveling wave solutions of seventh-order generalized KdV equations using he′s polynomials, International Journal of Nonlinear Sciences and Numerical Simulation. (2009) 10, no. 2, 227–233, 2-s2.0-65349085836.
10.1515/IJNSNS.2009.10.2.227
Web of Science® Google Scholar
46 Abbaoui K. and Cherruault Y., New ideas for proving convergence of decomposition methods, Computers and Mathematics with Applications. (1995) 29, no. 7, 103–108, 2-s2.0-0000487641.
10.1016/0898-1221(95)00022-Q
Web of Science® Google Scholar
47 Adomian G., Solving Frontier Problems of Physics: the Decomposition Method, 1994, Kluwer Academic Publishers, Boston, Mass, USA.
10.1007/978-94-015-8289-6
Google Scholar
48 Odibat Z. and Momani S., Numerical methods for nonlinear partial differential equations of fractional order, Applied Mathematical Modelling. (2008) 32, no. 1, 28–39, 2-s2.0-34548384362, https://doi.org/10.1016/j.apm.2006.10.025.
10.1016/j.apm.2006.10.025
Web of Science® Google Scholar

Citing Literature

All articles

An Efficient Approach for Fractional Harry Dym Equation by Using Sumudu Transform

Abstract

1. Introduction

2. Sumudu Transform

3. Basic Definitions of Fractional Calculus