Volume 2013, Issue 1 541935

Research Article

Open Access

A New Method Based on the RKHSM for Solving Systems of Nonlinear IDDEs with Proportional Delays

Changbo He,

Changbo He

School of Sports and Sciences, Harbin Normal University, Harbin, Heilongjiang 150025, China hrbnu.edu.cn

Search for more papers by this author

Xueqin Lv,

Corresponding Author

Xueqin Lv

[email protected]

School of Mathematics and Sciences, Harbin Normal University, Harbin, Heilongjiang 150025, China hrbnu.edu.cn

Search for more papers by this author

Jing Niu,

Jing Niu

School of Mathematics and Sciences, Harbin Normal University, Harbin, Heilongjiang 150025, China hrbnu.edu.cn

Search for more papers by this author

Changbo He,

Changbo He

School of Sports and Sciences, Harbin Normal University, Harbin, Heilongjiang 150025, China hrbnu.edu.cn

Search for more papers by this author

Xueqin Lv,

Corresponding Author

Xueqin Lv

[email protected]

School of Mathematics and Sciences, Harbin Normal University, Harbin, Heilongjiang 150025, China hrbnu.edu.cn

Search for more papers by this author

Jing Niu,

Jing Niu

School of Mathematics and Sciences, Harbin Normal University, Harbin, Heilongjiang 150025, China hrbnu.edu.cn

Search for more papers by this author

First published: 24 April 2013

https://doi.org/10.1155/2013/541935

Citations: 1

Academic Editor: Zhenya Yan

Share a link

Email
Wechat
Bluesky

Abstract

An efficient computational method is given in order to solve the systems of nonlinear infinite-delay-differential equations (IDDEs) with proportional delays. Representation of the solution and an iterative method are established in the reproducing kernel space. Some examples are displayed to demonstrate the computation efficiency of the method.

1. Introduction

In functional-differential equations (FDEs), there is a class of infinite-delay-differential equations (IDDEs) with proportional delays such systems are often encountered in many scientific fields such as electric mechanics, quantum mechanics, and optics. In view of this, developing the research for this class of IDDEs possesses great significance on theory and practice, for this attracts constant interest of researchers. Ones have found that there exist very different mathematical challenges between FDEs with proportional delays and those with constant delays. Some researches on the numerical solutions and the corresponding analysis for the linear FDEs with proportional delays have been presented by several authors. In the last few years, there has been a growing interest in studying the existence of solutions of functional differential equations with state dependent delay [1–7]. Initial-value problem for neutral functional-differential equations with proportional time delays had been studied in [8–11]; in the literature [11] authors had discussed the existence and uniqueness of analytic solution of linear proportional delays equations.

Ishiwata et al. used the rational approximation method and the collocation method to compute numerical solutions of delay-differential equations with proportional delays in [12, 13]. At [14–17], Hu et al. gave the numerical method to compute numerical solutions of neutral delay differential equations. For neutral delay differential equations with proportional delays, Chen and Wang proposed the variational iteration method [18] and the homotopy perturbation method [19]. Recently, time-delay systems become interested in applications like population growth models, transportation, communications, and agricultural models so those systems were widely studied both in a theoretical aspect and in that of related applications [20–22].

We consider the following nonlinear infinite delay-differential equation (IDDE) with proportional delay [23]:

()

where p ∈ (0,1), η is a given initial value, u(x) ∈ W₂[0, +∞), and for x ∈ [0, +∞), y, z ∈ (−∞, +∞), g(x, y, z) is a continuous function; g(x, y, z) ∈ W₁[0, +∞) as y = y(x), z = z(x) ∈ W₁[0, +∞).

Next, the following system of nonlinear infinite-delay-differential equations (IDDEs) with proportional delays will be studied:

()

where p, q ∈ (0,1), for x ∈ [0, +∞), y, z ∈ (−∞, +∞), f(x, y, z), g(x, y, z) are continuous bounded function, and f(x, y, z) ∈ W₁[0, +∞), g(x, y, z) ∈ W₁[0, +∞) as y = y(x), z = z(x). W₂[0, +∞) and W₁[0, ∞) are reproducing kernel spaces. Equations (2) are obtained through homogenization of initial condition for model in [24]. In this study, existence and a new iterative algorithm are established for the nonlinear infinite-delay-differential equations (IDDEs) with proportional delays in the reproducing kernel spaces.

The paper is organized as follows. In Section 2, some definitions of the reproducing kernel spaces are introduced. In Section 3, main results and the structure of the solution for operator equation are discussed. Existence of the solution to (2) and an iterative method are developed for the kind of problems in the reproducing kernel space. We verify that the approximate solution converges to the exact solution uniformly. In Section 4, some experiments are given to demonstrate the computation efficiency of the algorithm. The conclusion is given in Section 5.

2. Preliminaries

Definition 1 (see [25] reproducing kernel.)Let M be a nonempty abstract set. A function K : M × M → C is a reproducing kernel of the Hilbert space H if and only if

(a)
∀y ∈ M, K(·, x) ∈ H,
(b)
∀y ∈ M, ∀u ∈ H, 〈u(·), K(·, y)〉 = u(y).

The condition (b) is called “the reproducing property”; a Hilbert space which possesses a reproducing kernel is called a Reproducing Kernel Hilbert Space (RKHS).

Next, two reproducing kernel spaces are given.

Definition 2. W₂[0, +∞) = {u(x)∣u^′ is absolutely continuous real value functions, u^′′ ∈ L²[0, +∞), u(0) = 0}.

W₂[0, +∞) is a Hilbert space, for u(x), v(x) ∈ W₂[0, +∞); the inner product and norm in W₂[0, +∞) are given by

()

respectively.

Theorem 3. The space W₂[0, +∞) is a reproducing kernel space that is, for any u(y) ∈ W₂[0, +∞) and each fixed x ∈ [0, +∞), there exists R_x(y) ∈ W₂[0, +∞), y ∈ [0, +∞), such that u(x) = 〈R_x(y), u(y)〉. And the corresponding reproducing kernel can be represented as follows [26]:

()

Definition 4. W₁[0, +∞) = {u(x)∣u is absolutely continuous real-valued function, u^′ ∈ L²[0, +∞)}.

The inner product and norm in W₁[0, +∞) can be defined by

()

respectively, where u(x), v(x) ∈ W₁[0, +∞). It has been proved that W₁[0, +∞) is a complete reproducing kernel space and its reproducing kernel is as follows [27]:

()

3. Statements of the Main Results

In this section, the implementation method of obtaining the solution of (2) is proposed in the reproducing kernel space W₂[0, +∞).

Put the differential operator ℒ = d/dx; then we can convert (2) into the following form:

()

where x ∈ [0, +∞), and

()

It is clear that ℒ : W₂[0, +∞) → W₁[0, +∞) is a bounded linear operator. Let

, where

is dense in the interval [0, +∞), and ψ_i(x) = ℒ^*φ_i(x), where ℒ^* is the conjugate operator of ℒ. Define the normal orthogonal system

in W₂[0, +∞), which derives from Gram-Schmidt orthogonalization process of

()

Lemma 5. Assume that are dense in [0, +∞); then is a complete system in W₂[0, +∞) and .

Proof. Ones have

()

Clearly, ψ_i(x) ∈ W₂[0, +∞).

For any u(x) ∈ W₂[0, +∞), let 〈u(x), ψ_i(x)〉 = 0, i = 1,2, …, which means that

()

Note that

is dense in [0, +∞); therefore, ℒu(x) = 0. It follows that u(x) ≡ 0 from the existence of ℒ⁻¹.

3.1. Construction the of Iterative Sequence and

Next we construct the iterative sequence

and

, putting

()

where M_n(x), N_n(x) ∈ W₂[0, +∞) and

is a orthogonal projection operator. Then by (13) it followed that:

()

Lemma 6. Let be dense on [0, +∞); if the solution of (2) is unique, then the solution satisfies the form

()

Proof. Note that 〈u(x), φ_i(x)〉 = u(x_i) and is an orthonormal basis of W₂[0, +∞); hence according to Lemma 5 we have

()

In the same manner

()

Take u₀(x) = v₀(x) = 0; define the iterative sequence

()

3.2. The Boundedness of Sequence u_n(x) and v_n(x)

From

()

we have

()

where

()

;

; and

are bounded functions with respect to x, y, respectively.

Lemma 7. For x ∈ [0, +∞), y, z ∈ (−∞, +∞), and F(x, y, z), G(x, y, z) are continuous bounded functions on [0, +∞), we have that and are bounded.

Proof. By the expression of M_n(x), and the assumptions, we know that M_n(x) and are bounded. In the following, we will discuss the boundedness of .

Since the function which is in is dense in W₂[0, +∞), without loss of generality, we assume that is continuous.

Note that

()

One gets

()

where

. Thus, we have

()

Furthermore, we see that

()

In view of the expression of R_x(y), we know that

are bounded for m = 1, 2, 3. It follows that

is bounded from the boundedness of

, and

. In the same way, N_n(x),

, and

are bounded.

Lemma 8. Assume that F(x, y, z), G(x, y, z) are continuous bounded functions for x ∈ [0, +∞), y, z ∈ (−∞, +∞), and F(x, y, z), G(x, y, z) ∈ W₁[0, +∞) as y = y(x) ∈ W₂, z = z(x) ∈ W₂, then

()

Proof.

()

Note that (14) and the assumptions, by Lemma 7,

, i = 0, 1, 2, thus ∥M_n∥ ≤ C, where C = max {C⁰, C¹, C²}, from (19), we have

. In the same way, we obtain

3.3. Construction the of Another Iterative Sequence u_n(x) and v_n(x)

Theorem 9. Let be dense on [0, +∞); if the solution of (2) exists and unique, then the solution satisfies the form

()

Proof. Note that 〈u(x), φ_i(x)〉 = u(x_i) and is an orthonormal basis of W₂[0, +∞); hence we have

()

In the same manner

()

In the following, a new method of solving (2) is presented. Equations (31) and (32) can be denoted by

()

where

and

. In fact, A_i and B_i are unknown; we will approximate A_i and B_i by using the known

and

We take u₁(x) = 0, v₁(x) = 0 and define the following iterative sequence

()

where

()

Next, lemmas are given.

Lemma 10. The following iterative sequences

()

satisfy

()

respectively.

Proof. If j = 1,

()

so,

()

If j = 2,

()

β₂₁× (40) +β₂₂× (42), we have

()

by (41), ℒu_n(x₂) = F(x₂, u₂(x₂), v₂(px₂)). In the same way, we have

()

Similarly,

()

Theorem 11. The iterative form

()

and the iterative form

()

are the same.

Proof. In Lemma 10, let n − 1 = k; then

()

but

()

thus

()

Equation (46) can be written as

()

In fact,

; then

()

by (51) and (52), we have

()

Equation (53) is the same as (50). We may prove for

similarly.

So, by Theorem 11 and Lemma 8, we have the following Theorem.

Theorem 12. Under the conditions of Lemma 8,

()

satisfy ∥u_n(x)∥ ≤ C, ∥v_n(x)∥ ≤ D.

Lemma 13. If u(x) and v(x) ∈ W₂[0, +∞), then there exists M₁, M₂ > 0, such that |u(x)|≤ and .

Proof. It is easy to obtain from the properties in the reproducing kernel space.

By Lemma 13 and Theorem 12, it is easy to obtain the following Lemma 14.

Lemma 14. If , , x_n → y(n → ∞), and F(x, y, z) and G(x, y, z) satisfy the conditions of Lemma 8, then

()

Theorem 15. Let be dense in [0, +∞), and F(x, y, z) and G(x, y, z) satisfy the conditions of Lemma 8, then the n-term approximate solutions u_n(x) and v_n(x) in (35) converge to the exact solution u(x) and v(x) of (2), respectively, and , , where and are given, respectively, by (36), and (37).

Proof. (1) Firstly, we will prove the convergence of u_n(x), v_n(x).

By (35), we infer that

()

From the orthogonality of

, it follows that

()

From (59) and (60), we know sequence

and

is increasing. By Theorem 12,

and

are bounded; hence

and

are convergent such that

()

This implies that

()

Without loss of generality, assume m > n; we have

()

Considering the completeness of W₂[0, +∞), there exist

and

in W₂[0, +∞) such that

()

(2) Secondly, we will prove that and are the solutions of (2).

By Lemma 14 and the proof of (1), we may know that u_n(x), and v_n(x) respectively, converge uniformly to and . Taking limits in (35), we have

()

Since

()

in the same way, we have

()

it follows that

()

If n = 1, then

()

If n = 2, then

()

From (70) and (71), it is clear that

()

Furthermore, it is easy to see by induction that

()

Since

is dense in [0, +∞), for any y ∈ [0, +∞), there exists subsequence

such that

()

Hence, let j → ∞ in (74), and (75); by Lemma 14 and the continuity of F(x, u(x), v(px)) and G(x, v(x), u(qx)), we have

()

That is,

and

are the solutions of (2) and

()

where

and

In the proof of the convergence in Theorem 15 we only use ∥u_n∥ ≤ C, ∥v_n∥ ≤ D; thus we obtain the following corollary.

Corollary 16. Suppose ∥u_n∥ and ∥v_n∥ are bounded; then the iterative sequence (35) is convergent to the exact solution of (2).

Theorem 17. Assume u(x) and v(x) are the solutions of (2), and are the approximate errors of u_n(x), v_n(x), where u_n(x) and v_n(x) are given by (35). Then the errors , are monotone decreasing in the sense of .

Proof. From (35), and (79), it follows that

()

In the same way, we obtain from (35), (80)

()

Equations (81) and (82) show that the errors

and

are monotone decreasing in the sense of

4. Numerical Examples

In order to demonstrate the efficiency of our algorithm for solving (2), we will present two numerical examples in the reproducing kernel space W₂[0, +∞). Let n be the number of discrete points in [0, +∞). Denote , . All computations are performed by the Mathematica 5.0 software package. Results obtained by the method are compared with the exact solution of each example and are found to be in good agreement with each other.

Example 18. In this example we consider the problem

()

with exact solution u(x) = xe^−x, v(x) = sinx, and

, g(x) = −2e^−sinx + cos x − 4x³sin((1/2)xe^−x/2). Applying the presented method in Section 3, we calculate the approximate solution u₅₀(x) and v₅₀(x) in [0,1] as follows.

Step 1. By the method of the appendix, the corresponding reproducing kernel functions can be obtained.

Step 2. Choosing a dense subset in [0,1], then we get the orthogonalization coefficients β_ik.

Step 3. According to (10), we can get the normal orthogonal systems .

Step 4. Selecting the initial value u₀(x) = v₀(x) = 0, we obtain u₁(x), u₂(x), …, u₅₀(x) and v₁(x), v₂(x), …, v₅₀(x) by (19) developed in the paper.

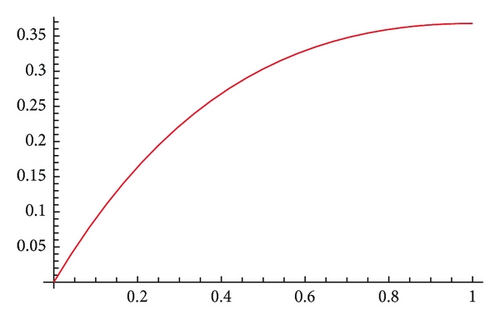
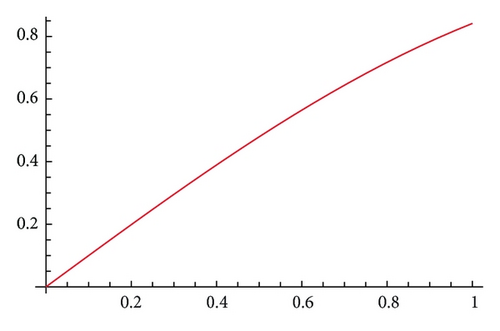
The graphs of the superimposed image emerge in Figure 1. At the same time, we have computed the approximate solutions u_n(x) and v_n(x) (n = 300, 900) in [0,3] and also calculated the relative errors and in Table 1. The root mean square errors (RMSE) about u(x) with u_n and v(x) with v_n are shown in Table 2.

Table 1. Relative errors in [0,3] for Example 18.

Node
0.3	4.97833e − 5	8.4527e − 5	5.53163e − 6	9.39806e − 6
0.6	4.43080e − 5	7.3330e − 5	4.92288e − 6	8.15664e − 6
0.9	3.86801e − 5	6.6731e − 5	4.29733e − 6	7.42512e − 6
1.2	3.41875e − 5	6.1845e − 5	3.79797e − 6	6.88400e − 6
1.5	3.09088e − 5	5.7095e − 5	3.43349e − 6	6.35872e − 6
1.8	2.87391e − 5	5.1303e − 5	3.19221e − 6	5.71898e − 6
2.1	2.75649e − 5	4.3153e − 5	3.06149e − 6	4.81984e − 6
2.4	2.7288e − 5	3.0422e − 5	3.03034e − 6	3.41736e − 6
2.7	2.7829e − 5	6.7566e − 5	3.09008e − 6	8.12936e − 7
3.0	2.90670e − 5	7.5017e − 5	3.23206e − 6	8.72219e − 6

Table 2. The RMS errors in [0,3] for Example 18.

n
300	9.95194e − 6	4.00007e − 5
900	1.10551e − 6	4.45554e − 6

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The left is the superimposed image of u(x) with u₅₀(x) in [0,1]. The right is the superimposed image of v(x) with v₅₀(x) in [0,1].

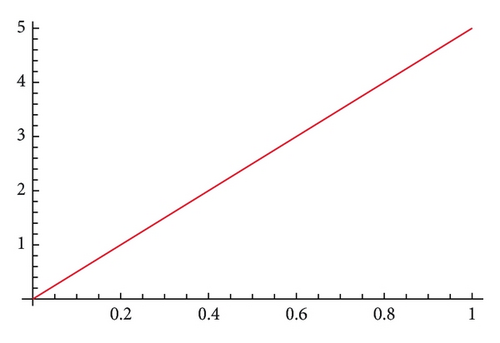
Example 19. Considering equations

()

The true solutions are u(x) = 5x, v(x) = 4tan(x), f(x) = 5 − 3cos (5x) − 2xsin(4tan(1/5)), g(x) = −4x³cos (5x/3) + 4secx² − 2sin(4tanx). The numerical results are given in Figure 2 and Tables 3 and 4. The figures and tables illustrate that the method given in the paper is efficient.

Table 3. Relative errors in [0,4] for Example 19.

Node
0.4	8.06470e − 5	4.94886e − 5	3.58334e − 5	2.20033e − 5
0.8	1.07473e − 4	5.27211e − 5	4.77632e − 5	2.34475e − 5
1.2	2.56877e − 4	5.32904e − 5	1.14199e − 4	2.37040e − 5
1.6	1.19110e − 4	5.01608e − 5	5.29170e − 5	2.23098e − 5
2.0	8.56122e − 5	4.35915e − 5	3.80383e − 5	1.93810e − 5
2.4	2.27843e − 4	3.52666e − 5	1.01280e − 4	1.56705e − 5
2.8	1.38237e − 4	2.74018e − 5	6.13912e − 5	1.21676e − 5
3.2	7.26035e − 5	2.15572e − 5	3.22429e − 5	9.56745e − 6
3.6	1.86684e − 5	1.80587e − 5	8.29627e − 5	8.01449e − 6
4.0	1.50042e − 4	1.64230e − 5	6.66348e − 5	7.14957e − 6

Table 4. The RMS errors in [0,4] for Example 19.

n
800	1.87807e − 3	7.85856e − 5
1200	8.34276e − 4	3.48826e − 5

5. Conclusion

In this paper, RKHSM has been successfully applied to find the solutions of systems of nonlinear IDDEs with proportional delays. The efficiency and accuracy of the proposed decomposition method were demonstrated by two test problems. It is concluded from above tables and figures that the RKHSM is an accurate and efficient method to solve IDDEs with proportional delays. Moreover, the method is also effective for solving some nonlinear initial-boundary value problems and nonlocal boundary value problems.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (61071181), the Educational Department Scientific Technology Program of Heilongjiang Province (12531180, 12512133, and 12521148), and the Academic Foundation for Youth of Harbin Normal University (KGB201226).

Appendix

The Reproducing Kernel Space W₂[0, m]

W₂[0, m] is defined as W₂[0, m] = {u(x)∣u^′ are absolutely continuous real value functions, u^′′ ∈ L²[0, m], u(0) = 0}. The inner product in W₂[0, m] is given by

()

where u, v ∈ W₂[0, m] and the norm

is denoted by

Theorem A.1. The space W₂[0, m] is a reproducing kernel space; that is, for any u(y) ∈ W₂[0, m] and each fixed x ∈ [0, m], there exists R_x(y) ∈ W₂[0, m], y ∈ [0, m], such that . The reproducing kernel R_x(y) can be denoted by

()

Proof. Applying to the integrations by parts for (A.1), we have

()

Since R_x(y) ∈ W₂[0, m], it follows that

()

For u(y) ∈ W₂[0, m], thus, u(0) = 0.

Suppose that R_x(y) satisfies the following generalized differential equations:

()

Then

. Hence, R_x(y) is the reproducing kernel of space W₂[0, m].

In the following, we will get the expression of the reproducing kernel R_x(y).

The characteristic equation of is given by λ⁴ − 5λ² + 4 = 0, and the characteristic roots are λ_1,2 = ±1, λ_3,4 = ±2.

We denote R_x(y) by

()

By the definition of space W₂[0, m], coefficients c₁, …, c₄, d₁, …, d₄ satisfy

()

from which, the unknown coefficients of (A.6) can be obtained:

()

References

1 Cooke K. L., J. Hale and J. LaSalle, Functional-differential equations: some models and perturbation problems, International Symposium on Differential Equations and Dynamical Systems, Held in Puerto Rico, 1967, Academic Press, New York, NY, USA, 167–183, MR0222409, ZBL0189.40301.
Google Scholar
2 Fečkan E., On certain type of functional differential equations, Mathematica Slovaca. (1994) 43, no. 1, 39–43.
Google Scholar
3 Grimm L. J., Existence and continuous dependence for a class of nonlinear neutral-differential equations, Proceedings of the American Mathematical Society. (1971) 29, no. 3, 467–473, MR0287117, ZBL0222.34061.
Web of Science® Google Scholar
4 Driver R. D., A two-body problem of classical electrodynamics: the one-dimensional case, Annals of Physics. (1963) 21, no. 1, 122–142, MR0151110, https://doi.org/10.1016/0003-4916(63)90227-6, ZBL0108.40705.
10.1016/0003-4916(63)90227-6
Web of Science® Google Scholar
5 Oberg R. J., On the local existence of solutions of certain functional-differential equations, Proceedings of the American Mathematical Society. (1969) 20, 295–302, MR0234094, https://doi.org/10.1090/S0002-9939-1969-0234094-6, ZBL0182.12602.
10.1090/S0002-9939-1969-0234094-6
Web of Science® Google Scholar
6 Jackiewicz Z., Existence and uniqueness of solutions of neutral delay-differential equations with state dependent delays, Funkcialaj Ekvacioj. (1987) 30, no. 1, 9–17, MR915257, ZBL0631.34006.
Google Scholar
7 Si J. G. and Wang X. P., Analytic solutions of a second-order iterative functional differential equation, Computers & Mathematics with Applications. (2002) 43, no. 1-2, 81–90, https://doi.org/10.1016/S0898-1221(01)00273-5, MR1873243, ZBL1008.34059.
10.1016/S0898-1221(01)00273-5
Web of Science® Google Scholar
8 Nussbaum R. D., Existence and uniqueness theorems for some functional differential equations of neutral type, Journal of Differential Equations. (1972) 11, no. 3, 607–623, MR0294825, https://doi.org/10.1016/0022-0396(72)90070-8, ZBL0263.34070.
10.1016/0022-0396(72)90070-8
Web of Science® Google Scholar
9 Kuang Y. and Feldstein A., Monotonic and oscillatory solutions of a linear neutral delay equation with infinite lag, SIAM Journal on Mathematical Analysis. (1990) 21, no. 6, 1633–1641, https://doi.org/10.1137/0521089, MR1075595, ZBL0719.34134.
10.1137/0521089
Web of Science® Google Scholar
10 Iserles A. and Liu Y., On functional-differential equations with proportional delays, 1993, no. DAMTP, 1993/NA3, Cambridge University.
Google Scholar
11 Liu Y. K., Stability analysis of θ-methods for neutral functional-differential equations, Numerische Mathematik. (1995) 70, no. 4, 473–485, https://doi.org/10.1007/s002110050129, MR1337227.
10.1007/s002110050129
Web of Science® Google Scholar
12 Ishiwata E. and Muroya Y., Rational approximation method for delay differential equations with proportional delay, Applied Mathematics and Computation. (2007) 187, no. 2, 741–747, https://doi.org/10.1016/j.amc.2006.08.086, MR2323079, ZBL1117.65105.
10.1016/j.amc.2006.08.086
Web of Science® Google Scholar
13 Ishiwata E., Muroya Y., and Brunner H., A super-attainable order in collocation methods for differential equations with proportional delay, Applied Mathematics and Computation. (2008) 198, no. 1, 227–236, https://doi.org/10.1016/j.amc.2007.08.078, MR2403944, ZBL1137.65047.
10.1016/j.amc.2007.08.078
Web of Science® Google Scholar
14 Hu P., Huang C., and Wu S., Asymptotic stability of linear multistep methods for nonlinear neutral delay differential equations, Applied Mathematics and Computation. (2009) 211, no. 1, 95–101, https://doi.org/10.1016/j.amc.2009.01.028, MR2517664.
10.1016/j.amc.2009.01.028
Web of Science® Google Scholar
15 Wang W., Zhang Y., and Li S., Stability of continuous Runge-Kutta-type methods for nonlinear neutral delay-differential equations, Applied Mathematical Modelling. (2009) 33, no. 8, 3319–3329, https://doi.org/10.1016/j.apm.2008.10.038, MR2524122, ZBL1205.65214.
10.1016/j.apm.2008.10.038
Web of Science® Google Scholar
16 Wang W. S. and Li S. F., On the one-leg θ-methods for solving nonlinear neutral functional differential equations, Applied Mathematics and Computation. (2007) 193, no. 1, 285–301, https://doi.org/10.1016/j.amc.2007.03.064, MR2385784.
10.1016/j.amc.2007.03.064
Web of Science® Google Scholar
17 Wang W., Qin T., and Li S., Stability of one-leg θ-methods for nonlinear neutral differential equations with proportional delay, Applied Mathematics and Computation. (2009) 213, no. 1, 177–183, https://doi.org/10.1016/j.amc.2009.03.010, MR2533374.
10.1016/j.amc.2009.03.010
Web of Science® Google Scholar
18 Chen X. and Wang L., The variational iteration method for solving a neutral functional-differential equation with proportional delays, Computers & Mathematics with Applications. (2010) 59, no. 8, 2696–2702, https://doi.org/10.1016/j.camwa.2010.01.037, MR2607972, ZBL1193.65145.
10.1016/j.camwa.2010.01.037
Web of Science® Google Scholar
19 Biazar J. and Ghanbari B., The homotopy perturbation method for solving neutral functional differential equations with proportional delays, Journal of King Saud University. (2012) 24, no. 1, 33–37, https://doi.org/10.1016/j.jksus.2010.07.026.
10.1016/j.jksus.2010.07.026
Google Scholar
20 De la Sen M., Stability of impulsive time-varying systems and compactness of the operators mapping the input space into the state and output spaces, Journal of Mathematical Analysis and Applications. (2006) 321, no. 2, 621–650, https://doi.org/10.1016/j.jmaa.2005.08.038, MR2241144, ZBL1111.93072.
10.1016/j.jmaa.2005.08.038
Web of Science® Google Scholar
21 De la Sen M., Agarwal R. P., Ibeas A., and Alonso-Quesada S., On a generalized time-varying SEIR epidemic model with mixed point and distributed time-varying delays and combined regular and impulsive vaccination controls, Advances in Difference Equations. (2010) 2010, 42, 281612, MR2771485, ZBL1219.34104, https://doi.org/10.1155/2010/281612.
10.1186/1687-1847-2010-281612
Google Scholar
22 Fridman E. and Orlov Y., Exponential stability of linear distributed parameter systems with time-varying delays, Automatica. (2009) 45, no. 1, 194–201, https://doi.org/10.1016/j.automatica.2008.06.006, MR2531511, ZBL1154.93404.
10.1016/j.automatica.2008.06.006
Web of Science® Google Scholar
23 Lü X. and Cui M., Analytic solutions to a class of nonlinear infinite-delay-differential equations, Journal of Mathematical Analysis and Applications. (2008) 343, no. 2, 724–732, https://doi.org/10.1016/j.jmaa.2008.01.101, MR2401528, ZBL1160.34059.
10.1016/j.jmaa.2008.01.101
Web of Science® Google Scholar
24 Zhang C. and Sun G., Nonlinear stability of Runge-Kutta methods applied to infinite-delay-differential equations, Mathematical and Computer Modelling. (2004) 39, no. 4-5, 495–503, https://doi.org/10.1016/S0895-7177(04)90520-1, MR2046536, ZBL1068.65106.
10.1016/S0895-7177(04)90520-1
Google Scholar
25 Lv X. and Gao Y., The RKHSM for solving neutral functional-differential equation with proportional delays, Mathematical Methods in the Applied Sciences. 36, no. 6, 642–649, https://doi.org/10.1002/mma.2612.
10.1002/mma.2612
Web of Science® Google Scholar
26 Minggen C. and Zhongxing D., Solution to the definite solution problem of differential equations in space , Advance in Mathematics. (1986) 17, 327–328.
Google Scholar
27 Li C. l. and Cui M. G., The exact solution for solving a class nonlinear operator equations in the reproducing kernel space, Applied Mathematics and Computation. (2003) 143, no. 2-3, 393–399, https://doi.org/10.1016/S0096-3003(02)00370-3, MR1981704, ZBL1034.47030.
10.1016/S0096-3003(02)00370-3
Web of Science® Google Scholar

Citing Literature

All articles

A New Method Based on the RKHSM for Solving Systems of Nonlinear IDDEs with Proportional Delays

Abstract

1. Introduction

2. Preliminaries

3. Statements of the Main Results

3.1. Construction the of Iterative Sequence and

3.2. The Boundedness of Sequence u_n(x) and v_n(x)

3.3. Construction the of Another Iterative Sequence u_n(x) and v_n(x)

4. Numerical Examples

5. Conclusion

Acknowledgments

Appendix

The Reproducing Kernel Space W₂[0, m]

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A New Method Based on the RKHSM for Solving Systems of Nonlinear IDDEs with Proportional Delays

Abstract

1. Introduction

2. Preliminaries

3. Statements of the Main Results

3.1. Construction the of Iterative Sequence and

3.2. The Boundedness of Sequence un(x) and vn(x)

3.3. Construction the of Another Iterative Sequence un(x) and vn(x)

4. Numerical Examples

5. Conclusion

Acknowledgments

Appendix

The Reproducing Kernel Space W2[0, m]

References

Citing Literature

Figures

References

Related

Information

3.2. The Boundedness of Sequence u_n(x) and v_n(x)

3.3. Construction the of Another Iterative Sequence u_n(x) and v_n(x)

The Reproducing Kernel Space W₂[0, m]