Considering two-dimensional compressible miscible displacement flow in porous media, finite difference schemes on grids with local refinement in time are constructed and studied. The construction utilizes a modified upwind approximation and linear interpolation at the slave nodes. Error analysis is presented in the maximum norm and numerical examples illustrating the theory are given.

1. Introduction

Numerical models of percolation flow are almost built up on a basis of the finite difference method to solve the system of partial differential equations. Usually, grids that we used are thinner, then the truncation error is smaller and the computing accuracy is higher. In order to assure certain computation accuracy, the grid number cannot be too little. But on the other hand, along with the increment of the grid number, the computation cost is greatly increased and the algebraic system which is formed finally cannot be resolved, even with the largest of today’s supercomputers. Actually, we only need to refine grids around wells, cracks, obstacles, domain boundaries, and so forth, where the pressure changes radically. But because the finite difference grid is composed of straight lines and the grid density cannot be varied with space, it limits the simulating scale and the simulating accuracy. For the local grid refinement technique, we still make use of the finite difference grid system and divide partial grids which are needed to be refined into fine grids. In this way, we can resolve problems, such as small well spacing, fault, and boundary, and we can improve the simulating accuracy and extend the simulating scale [1].

Ewing et al. construct some finite difference approximations on grids with local refinement in space for the ellipse equation and obtain error estimates in the H¹-norm [2]. Cai et al. analyze stationary local grid refinement for the diffusion equation [3, 4]. Ewing et al. derive implicit schemes on the basis of a finite volume approach by approximation of the balance equation. This approach leads to schemes that are locally conservative and are absolutely stable [5]. Ewing et al. construct and study finite difference schemes for transient convection-diffusion problems on grids with local refinement in time and space. The proposed schemes are unconditionally stable and use linear interpolation along the interface [6]. Respectively for incompressible miscible displacement flow in porous media and the semiconductor device problem, authors discuss discrete schemes, error estimates, and numerical examples on composite triangular grids [7, 8].

In this paper, we study a finite difference scheme on grids with local refinement in time for two-dimensional compressible miscible displacement flow in porous media. The pressure equation is approximated by a five-point difference scheme, and the saturation equation is discretized by a modified upwind scheme. At the slave nodes, the construction utilizes linear interpolation. Finally, error analysis in the maximum norm is derived and numerical examples are given to support the numerical method and its convergence.

The paper is organized as follows. In Sections 2 and 3, we formulate the problem and introduce the necessary notations. In Section 4 the construction of the finite difference scheme is presented. The error analysis is addressed in Section 5. Finally, in Section 6 we present numerical experiments that conform our theoretical results.

2. Problem Formulation

We will consider a system of three nonlinear partial differential equations in a bounded domain Ω ⊂ R², which forms a basic model of compressible miscible displacement flow in porous media [9–11]:

()

where

()

c_i (i = 1,2) is the saturation of the ith component in mixed liquid, Z_j is the jth component of compression constant factor, ϕ is the porosity of the rock, k is the permeability of the rock, μ is the viscosity of the fluid, D = ϕ(x)d_mI which is the 2 × 2 diffusion matrix, d_m is the diffusion coefficient, and I is the unit matrix. The unknowns are the pressure function p(x, t) and the saturation function c(x, t).

In addition, we have boundary conditions

()

and initial conditions

()

where Ω is a plane bounded domain and ∂Ω is the boundary of Ω.

Usually this question is positive. Suppose the coefficients of (1) satisfy

()

where a_*, a^*, d_*, d^*, D_*, D^*, K^* are positive constants and d(c), b(c), and f(c) are Lipschitz continuous in the ε₀ neighborhood of the solution.

We suppose that the exact solutions of (1) are distributed smoothly; p and c satisfy

()

Throughout this paper, the notations K_i (i = 0,1, …, M) are used to denote generic constants.

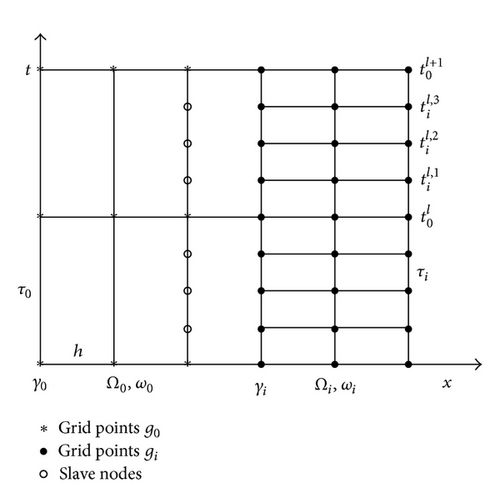
3. Grids, Grid Functions, and Associated Notations

First, Ω = [0,1] ² is discretized using a regular grid with a parameter h. The spatial nodes of the grid on Ω are then defined by x = (x₁, x₂) = (n₁h, n₂h), where n₁ = 0, …, N, n₂ = 0, …, N, h = 1/N. Next, we introduce closed domains , which are subsets of Ω with boundaries aligned with the spatial discretization already defined. Further, it is required that , and we set . In order to avoid unnecessary complications, for i, j > 0, we assume that dist(Ω_i, Ω_j) ≥ lh, where l > 1 is an integer.

With each subdomain Ω_i, we associate corresponding sets of nodal points: ω_i is defined to be the set of all nodes of the discretization of Ω that are in Ω_i. We require ω_i ⋂ ω_j = ∅, for i ≠ j, i, j = 0, …, M. And assume that there is no spatial refinement. In each ω_i, i = 0, …, M, we define a subset of boundary nodes γ_i as the nodes which have at least one neighbor not in ω_i. Then set .

A discrete time-step τ_i is associated with each Ω_i such that, for integers m_i,

()

Consequently, discrete time levels

for Ω_i are defined by

, j = 1,2, …, [T/τ_i]. Finally, we define the grid points g by setting

()

We continue by specifying the nodes in g_i between time levels

and

()

Correspondingly, the boundary nodes of

are defined by

()

The grid function y(x, t) is a function defined at the grid points of g. we denote the nodal values of a grid function y(x, t) between time levels

and

()

for x ∈ ω_i, i > 0, j = 0, …, m_i. For x ∈ ω₀ we define

()

and

are the divided forward and backward difference operators, respectively, in x₁ and x₂ direction. Also define the divided backward time difference by

()

4. Construction of the Finite Difference Schemes

Let P, U, and C be the numerical approximations to the pressure p, the velocity u, and the saturation c, respectively. The approximation for the pressure and the concentration approximation are done on composite grids in time.

First for the pressure equation, we let

()

Similarly we define

, then let

()

For regular coarse grids, the five-point difference scheme is

()

where the difference operator

. The Darcy velocity

is computed as follows:

()

corresponds to another direction, and the computational formula is similar to

Next we consider the saturation equation (1)(c). The positive and negative of the function v are defined as v⁺ = (1/2)(v+|v|) ≥ 0 and v⁻ = (1/2)(v−|v|) ≤ 0. For regular coarse grids, the upwind difference scheme of the saturation equation is

()

where

()

In the region that is refined in time, we can construct finite difference schemes similar to (16)–(18). It is obvious that at time

, j = 1, …, m_i, when the difference operators defined above are applied to the points of γ_i, not all space-time positions required correspond to actual nodes in g. For such cases, we define

()

In Figure 1, the slave nodes represent the missing space-time positions in the stencil of nodes in

. The values there are computed by the interpolation formula (20).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Grid with local refinement in time.

The discretization schemes of (1)–(4) on composite grids are given by

()

correspond to another direction, and computational formulae are similar to (22).

()

5. Error Analysis

The discrete inner product and L²-norm of grid functions are defined, respectively, by

()

We also use the standard notation for the discrete H¹-norm of a grid function in the Sobolev space

()

Define the error of the above scheme by

()

Firstly consider the pressure equation. Using (1)(a) and (21), we get the error equation:

()

Using (27)(b), we can get

()

Then using the maximum principle

()

With the method of recursion and noticing that

, we obtain the error estimate:

()

Similarly using (27)(c) and (27)(d),

()

Then we consider the saturation equation. Suppose that

()

where

is a positive constant. In the end of error analysis, we will prove the supposition (32). Under the supposition (32), we can prove the discretizations (23) satisfy the following property.

Theorem 1. The finite difference schemes (23) comply with the requirements of the maximum principle and the difference operator is coercive in , that is, ∃μ > 0 such that

()

Considering

()

and using (1)(c), (23), we can get the error equation of the saturation equation

()

We need an induction hypothesis. Let τ₀ = O(h), we assume that

()

for

. When

, we can obtain (36) by using (4) and (23). At the end of error analysis, we will prove (36) for

From error estimates of the pressure equation (30) and (31) and the induction hypothesis (36), we have

()

In order to get an estimate for the error ξ(x, t), we need two types of auxiliary functions ψ_i and φ_i. The grid functions

and

, respectively, satisfy

()

where χ_i(x) is the characteristic function of ω_i∖γ_i, χ₀(x) is the characteristic function of ω₀, and α_i(x) is the characteristic function of γ_i. On condition that

is coercive in

, Ewing et al. have proved ψ_i and φ_i satisfy the following lemma [6].

Lemma 2. and exist and are nonnegative, and the following estimates hold:

()

Theorem 3. Let the exact solutions c(x, t) of (1) satisfy the condition (6), then the discretization scheme (23) is stable, and if τ₀ = O(h) the following estimate for the error holds:

()

Proof. Define

()

where

. Using induction over l, it easy to observe that

()

Moreover,

()

Using the maximum principle, it follows that

()

Similarly,

()

Therefore,

()

Then in view of (39), we conclude (40).

It remains to check (32) and the induction hypothesis (36) for . From τ₀ = O(h) and the error estimate (40), it is easy to obtain (36). Then using (30) and (31), (34), and (40), we can obtain the supposition (32). The proof of Theorem 3 is complete.

6. Numerical Results

We consider a system of coupled partial differential equations:

()

where Ω = [0,2] ², J = [0, T]. The following functions are used as exact solutions of (47):

()

When t = 0.5 and t = 1, exact solutions of (47) are shown in Figures 2 and 3. Specific forms of c₀, c_l, c_r, q, and f are derived by exact solutions.

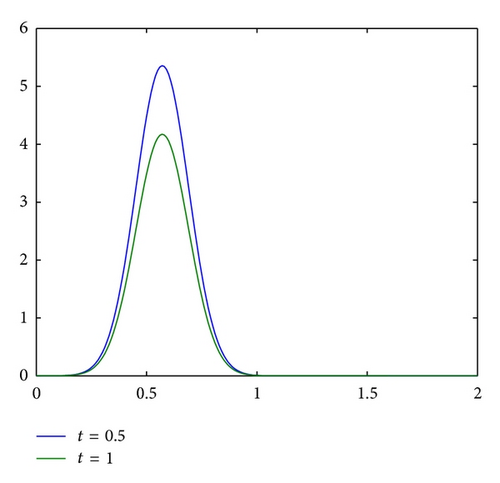
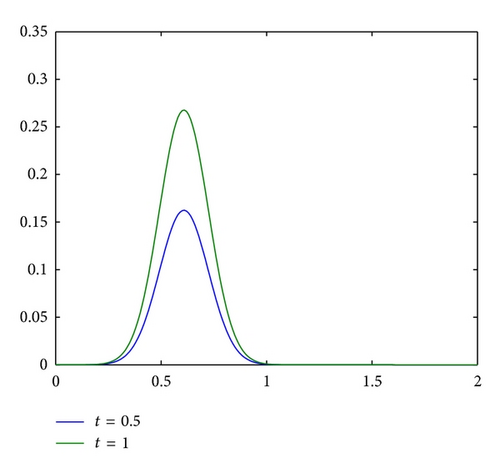
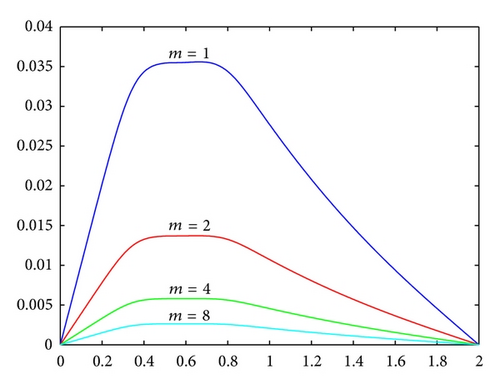
From Figures 2 and 3, we can see exact solutions of (47) possess highly localized properties in [0.2,1] ². First, Ω is discretized using a regular grid. Let the space-step h = 1/160 and the time-step τ₀ = h. Then choose the subregion Ω₁ = [0,1.3] ², which is refined in time. Let the discretization parameters τ^′ = τ₀/m in the refined region Ω₁, where m is a positive integer. We denote by C the numerical approximation to c obtained by (23). And let the error estimate in maximum norm γ = max_g|c − C|.

Example 4. Let D(x) = 1. Choosing m = 1,2, 4,8, computational results obtained by (23) are shown in Figures 4 and 5 and Table 1.

Table 1. Error estimate in maximum norm when D(x) = 1.

m	t = 0.5			t = 1
m	Computational cost	γ	Reduction	Computational cost	γ	Reduction
1	0.1560	0.0159		0.3130	0.0356
2	0.5780	0.0062	2.56	1.1560	0.0137	2.60
4	2.3440	0.0026	2.38	4.6080	0.0058	2.36
8	9.2810	0.0012	2.17	18.6800	0.0026	2.23

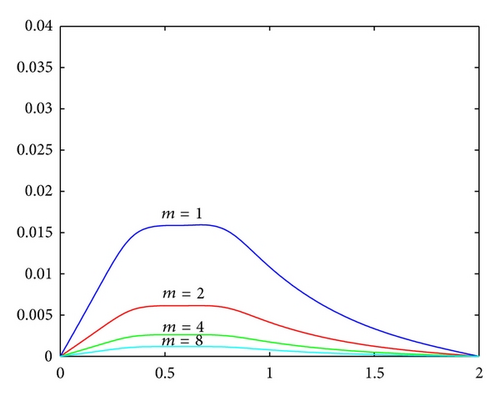
Example 5. Let D(x) = x. Choosing m = 1,2, 4,8, computational results obtained by (23) are shown in Table 2.

Table 2. Error estimate in maximum norm when D(x) = x.

m	t = 0.5			t = 1
m	Computational cost	γ	Reduction	Computational cost	γ	Reduction
1	0.1710	0.0535		0.3270	0.1342
2	0.5920	0.0254	2.11	1.1680	0.0641	2.10
4	2.3840	0.0124	2.05	4.6590	0.0313	2.05
8	9.8810	0.0061	2.03	19.7440	0.0154	2.03

From Figures 4 and 5 and Tables 1 and 2, we can see that numerical results produced by using the local refinement technique are more accurate than those produced without refinement. From Tables 1 and 2, we observe a monotonic improvement of the accuracy in maximum norm when using difference refinement factors m. These results are of great importance for the research on numerical simulation of the fluid flow problem and also indicate that the method proposed in this paper can be widely applied to some application fields, such as energy numerical simulation and environmental science.

Acknowledgments

The author thanks Professor Yirang Yuan for his valuable constructive suggestions which lead to a significant improvement of this paper. This work is supported in part by the National Natural Science Foundation of China (Grant no. 71071088) and the Natural Science Foundation of Shandong Province of China (Grant no. ZR2011AQ021).

References

1 Yuan Y. R., Some new progress in the fileds of computational petroleum geology and others, Chinese Journal of Computational Physics. (2003) 20, no. 4, 283–290.
Google Scholar
2 Ewing R. E., Lazarov R. D., and Vassilevski P. S., Local refinement techniques for elliptic problems on cell-centered grids. I. Error analysis, Mathematics of Computation. (1991) 56, no. 194, 437–461, https://doi.org/10.2307/2008390, MR1066831, ZBL0724.65093.
10.2307/2008390
Web of Science® Google Scholar
3 Cai Z. Q., Mandel J., and McCormick S. F., The finite volume element method for diffusion equations on general triangulations, SIAM Journal on Numerical Analysis. (1991) 28, no. 2, 392–402, https://doi.org/10.1137/0728022, MR1087511, ZBL0729.65086.
10.1137/0728022
Web of Science® Google Scholar
4 Cai Z. Q. and McCormick S. F., On the accuracy of the finite volume element method for diffusion equations on composite grids, SIAM Journal on Numerical Analysis. (1990) 27, no. 3, 636–655, https://doi.org/10.1137/0727039, MR1041256, ZBL0707.65073.
10.1137/0727039
Web of Science® Google Scholar
5 Ewing R. E., Lazarov R. D., and Vassilevski P. S., Finite difference schemes on grids with local refinement in time and space for parabolic problems. I. Derivation, stability, and error analysis, Computing. (1990) 45, no. 3, 193–215, https://doi.org/10.1007/BF02250633, MR1080791, ZBL0721.65047.
10.1007/BF02250633
Web of Science® Google Scholar
6 Ewing R. E., Lazarov R. D., and Vassilev A. T., Finite difference scheme for parabolic problems on composite grids with refinement in time and space, SIAM Journal on Numerical Analysis. (1994) 31, no. 6, 1605–1622, https://doi.org/10.1137/0731083, MR1302677, ZBL0817.65071.
10.1137/0731083
Web of Science® Google Scholar
7 Liu W. and Yuan Y. R., Finite difference schemes for two-dimensional miscible displacement flow in porous media on composite triangular grids, Computers & Mathematics with Applications. (2008) 55, no. 3, 470–484, https://doi.org/10.1016/j.camwa.2007.05.003, MR2384160, ZBL1155.65371.
10.1016/j.camwa.2007.05.003
Web of Science® Google Scholar
8 Liu W. and Yuan Y. R., A finite difference scheme for two-dimensional semiconductor device of heat conduction on composite triangular grids, Applied Mathematics and Computation. (2012) 218, no. 11, 6458–6468, https://doi.org/10.1016/j.amc.2011.12.017, MR2879126.
10.1016/j.amc.2011.12.017
Web of Science® Google Scholar
9 Douglas,J.Jr. and Roberts J. E., Numerical methods for a model for compressible miscible displacement in porous media, Mathematics of Computation. (1983) 41, no. 164, 441–459, https://doi.org/10.2307/2007685, MR717695, ZBL0537.76062.
10.1090/S0025-5718-1983-0717695-3
Web of Science® Google Scholar
10 Yi Yuan R., Time stepping along charcteristics for the finite element approximation of compressible miscible displacement in porous media, Mathematica Numerica Sinica. (1992) 14, no. 4, 385–406.
Google Scholar
11 Yang J. M. and Chen Y. P., A priori error analysis of a discontinuous Galerkin approximation for a kind of compressible miscible displacement problems, Science China, Mathematics. (2010) 53, no. 10, 2679–2696, https://doi.org/10.1007/s11425-010-3128-2, MR2728271.
10.1007/s11425-010-3128-2
Web of Science® Google Scholar

All articles

A Finite Difference Scheme for Compressible Miscible Displacement Flow in Porous Media on Grids with Local Refinement in Time

Abstract

1. Introduction

2. Problem Formulation

3. Grids, Grid Functions, and Associated Notations

4. Construction of the Finite Difference Schemes

5. Error Analysis

6. Numerical Results

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Finite Difference Scheme for Compressible Miscible Displacement Flow in Porous Media on Grids with Local Refinement in Time

Abstract

1. Introduction

2. Problem Formulation

3. Grids, Grid Functions, and Associated Notations

4. Construction of the Finite Difference Schemes

5. Error Analysis

6. Numerical Results

Acknowledgments

References

Figures

References

Related

Information