Abstract and Applied Analysis
Volume 2013, Issue 1 508450
Research Article
Open Access

Algebraic Structures Based on a Classifying Space of a Compact Lie Group

Dae-Woong Lee, 

Corresponding Author

Dae-Woong Lee

Department of Mathematics and Institute of Pure and Applied Mathematics, Chonbuk National University, 567 Baekje-daero, Deokjin-gu, Jeonju-si, Jeollabuk-do 561-756, Republic of Korea chonbuk.ac.kr

Search for more papers by this author
First published: 07 November 2013
https://doi.org/10.1155/2013/508450
Academic Editor: Teoman Özer

Abstract

We analyze the algebraic structures based on a classifying space of a compact Lie group. We construct the connected graded free Lie algebra structure by considering the rationally nontrivial indecomposable and decomposable generators of homotopy groups and the cohomology cup products, and we show that the homomorphic image of homology generators can be expressed in terms of the Lie brackets in rational homology. By using the Milnor-Moore theorem, we also investigate the concrete primitive elements in the Pontrjagin algebra.

1. Introduction

A Lie group is a differentiable manifold M with a group structure in which the multiplication M × M → M and the inversive map M → M (m ↦ m−1) are differentiable. Therefore, it can be studied using differential calculus in contrast with the case of more general topological groups as a special case of H-spaces. It is well known that the only spheres that are connected H-spaces are S1, S3, and S7. We note that the first two spheres are Lie groups while the last one is just an H-space which is not an A3-space but just an A2-space in the sense of Stasheff [1]. Lie groups play an enormous role in algebraic topology as well as modern differential geometry on several different levels. The presence of continuous symmetries expressed via a Lie group action on a manifold places strong constraints on its geometry and facilitates analysis on the manifold. Moreover, linear actions of Lie groups are especially important and are studied in representation theory.

As usual we let Σ and Ω be the suspension and loop functors in the (pointed) homotopy category, respectively. It is well known that the functors Σ and Ω are examples of adjoint functors. Moreover, co-H-spaces and H-spaces are important objects of research in homotopy theory and they are the dual notions in the sense of Eckmann and Hilton. We refer to Arkowitz’s paper [2] and Scheerer’s article [3] for a survey of the vast literature about co-H-spaces, H-spaces, and related topics.

Let SNT(X) denote the set of all homotopy types [Y] such that X and Y have the same n-type for each nonnegative integer n (see [4–6]). McGibbon and Møller [7] showed that if G is a connected compact Lie group, then its classifying space usually has an uncountable SNT(BG) except for several cases and gave an excellent set of examples. Furthermore, in [8] the classical projective n-spaces (real, complex, and quaternionic) were studied in terms of their self-maps from a homotopy point of view. Recently, some common fixed point results for single as well as set valued mappings involving certain rational expressions in complete partial metric spaces were obtained in [9]. Moreover, some fixed point and common fixed point theorems on ordered cone b-metric spaces were also established in [10].

In this paper all spaces are based and have the based homotopy type of based, connected CW-complexes. All maps and homotopies preserve the base point. Unless otherwise stated, we do not distinguish notationally between a map and its homotopy class.

The main purpose of this paper is to investigate the algebraic explanation based on a classifying space of the compact Lie group U(1). After constructing self-maps using the suspension structure, we define a useful commutator of self-maps on the suspension of a classifying space of the compact Lie group. We construct the connected graded free Lie algebra structure by considering the rationally nontrivial indecomposable and decomposable generators of homotopy groups and the cohomology cup products. We show that the homomorphic image of homology generators can be expressed in terms of the Lie brackets in rational homology. By using the Milnor-Moore theorem, we also investigate the concrete primitive elements as the images of the Hurewicz homomorphisms in the Pontrjagin algebra.

2. Preliminaries

Let ℤ, ℚ, ℝ, and ℂ denote the ring of integers, the fields of rational, real, and complex numbers, respectively. The unitary group  U(n) is the group of n × n unitary matrices with the group operation that of matrix multiplication as a subgroup of the general linear group GL(n, ℂ). The unitary group U(n) is a real Lie group of dimension n2. The Lie algebra of U(n) consists of n  ×  n skew-Hermitian matrices with the Lie bracket given by the commutator. The first unitary group   U(1) is canonically the circle group consisting of all complex numbers with absolute value 1 under multiplication; that is, the set of all 1 × 1 unitary matrices. The first unitary group shows up in a variety of forms in mathematics. Some of the more common forms are as follows:
()
where T is a one torus and SO(2) is the orthogonal 2 × 2 matrices with determinant 1. The latter is said to be the special orthogonal group.

A classifying space  BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G. It has the property that any principal G-bundle over a paracompact manifold is isomorphic to a pullback of the principal bundle EG → BG. We note that the classifying space functor B is essentially inverse to the loop space functor Ω in algebraic topology.

If X is a co-H-group with comultiplication
()
and homotopy inverse, then for every pointed space Y the set [X, Y] of homotopy classes from X to Y can be given the structure of a group under the addition as follows: for a, b ∈ [X, Y], the binary operation, denoted “a + b”, is defined by the homotopy class of the composition of maps
()
where ∇ is a folding map.
The Eckmann-Hilton dual of a co-H-group is an H-group (see [11, 12]). As an adjointness, if X is any pointed space and (Y, m) is an H-group, then the set [X, Y] becomes a group if we define the product “c · d” to be the homotopy class of the composition of maps
()
where Δ : X → X × X is the diagonal map, c, d ∈ [X, Y], and m : X × X → X is a multiplication.

The principle examples of a co-H-group and an H-group are the suspension ΣX and the loop space ΩX of a space X, respectively.

We note that BU(1) has a CW-decomposition as follows:
()
where γn is an attaching map for n = 1,2, 3, ….

From now on, we denote BU(1) k by the k-skeleton of a CW-complex BU(1). We define maps fn : BU(1) → ΩΣBU(1) for n = 1,2, 3, … as follows.

Definition 1. The cofibration sequence

()
induces an exact sequence of groups
()
for each n = 1,2, 3, …. We now take an essential map
()
for each n = 1,2, 3, …. Similarly, by using the above exact sequences, we can choose an essential map
()
such that for n = 1,2, 3, ….

In the above definition, we note that BU(1) 1 = *, and thus is an isomorphism. We also note that
()

We now define the following.

Definition 2. We define a rationally nontrivial homotopy element

()
of the homotopy groups modulo torsions π2n(ΩΣBU(1))/torsion by for each n = 1,2, 3, ….

Now we take the self-map
()
by the adjointness of
()
for each n = 1,2, 3, ….
We recall that
()
as a graded ℚ-module, where un is the standard generator of H2n(BU(1); ℚ) for each n = 1,2, 3, …. The salient Bott-Samelson theorem [13] says that the Pontrjagin algebra H*(ΩΣBU(1); ℚ) is isomorphic to the tensor algebra TH*(BU(1); ℚ). In other words, the rational homology of ΩΣK is the tensor algebra T{u1, u2, …, un, …} generated by {u1, u2, …, un, …}, where un is a rational homology generator with diagonal
()
and un = E*(un). Here, E is the canonical inclusion map E : BU(1) → ΩΣBU(1) defined by E(s)(t) = 〈s, t〉 ∈ ΣBU(1), and u0 means 1. From the Serre spectral sequence of a fibration ΩBU(1) → PBU(1) → BU(1), we have an algebra isomorphism
()
Here ℚ[α] is the polynomial algebra over ℚ generated by α of degree 2; that is, α is a generator of H2(BU(1); ℚ) with the Kronecker index 〈αi, uj〉 = δij.

We now consider a wedge of spheres for 2 ≤ n1 ≤ n2 ≤ ⋯≤nk. Let be the tth inclusion for t = 1,2, …, k. We then inductively define and order basic (Whitehead) products as follows. Basic products of weight 1 are (in order) r1, r2, …, rk. Assume basic products of weight < n have been defined and ordered so that if r < s < n, any basic product of weight r is less than all basic products of weight s. Then a basic product of weight n is a Whitehead product [a, b], where a is a basic product of weight m and b is a basic product of weight l, m + l = n, a < b. Furthermore, if b is a Whitehead product [c, d] of basic products c and d, then we require that c ≤ a. The basic products of weight n are ordered arbitrarily among themselves and are greater than any basic product of weight < n. Note that to a basic product of weight n we can associate a string of distinct symbols , for 1 ≤ vi ≤ k, which are the elements which appear in the basic products. Suppose in the basic product ws, rp occurs lp times, lp ≥ 1. Then the height of the basic product is ∑lp(rp − 1) + 1 and the length is ∑lp − 1. Clearly if ws has height hs, then .

We end this section with the following Hilton’s formula [14].

Theorem 3. Let the ordered basic products of be w1, w2, …, ws, … with the height of ws = hs. Then for every m,

()
The isomorphism is defined by
()

We note that the direct sum is finite for each m since hs → ∞.

3. Commutators and Lie Algebra Structures

By using the addition of a co-H-group in Section 2, we define the following.

Definition 4. We define a commutator

()
of and in [ΣBU(1), ΣBU(1)] by
()
where the operations are the suspension additions on ΣBU(1), and
()
is the suspension inverse defined by
()
for s ∈ BU(1) and t ∈ I.

Let

()
be the map of loop inverse given by l(ω) = ω−1, where ω−1(t) = ω(1 − t), t ∈ I.

Similarly, we define the following.

Definition 5. The map is a commutator of and in [BU(1), ΩΣBU(1)] defined by

()
where s ∈ BU(1), and the multiplication is the loop multiplication.

Remark 6. Let be a map given by

()
Then we get
()
where Δ : BU(1) → BU(1) × BU(1) is the diagonal map.

Note that the weak category of ΩΣBU(1) is not finite because there are infinitely many nonzero cohomology cup products in it, and thus it has the infinite Lusternik-Schnirelmann category [12, Chapter X]. Moreover, Arkowitz and Curjel [15, Theorem 5] showed that the n-fold commutator is of finite order if and only if all n-fold cup products of any positive dimensional rational cohomology classes of a space vanish (see also [16]). Therefore, we can consider the iterated commutators which are nontrivial in ΩΣBU(1).

We recall that the Samelson product gives π*(ΩX), * ≥ 1, the structure of graded Lie algebra (see [17, 18]); that is, if x ∈ πp(ΩX), y ∈ πq(ΩX) and z ∈ πr(ΩX), then
()

Let k1 : X → X × X and k2 : X → X × X be the first and second inclusions between based spaces, respectively; that is, k1(x) = (x, x0) and k2(x) = (x0, x), where x0 is the base point of X. Recall that an element z ∈ H*(X) is said to be primitive if and only if in homology, where Δ : X → X × X is the diagonal map.

Let h : π*(ΩX) → H*(ΩX; ℚ) be the Hurewicz homomorphism. In 1965, Milnor and Moore [19] proved the following salient theorem (see also [18, page 293]).

Theorem 7. If X is a simply connected topological space and if 𝔽 is a field of characteristic zero, then

  • (1)

    the Samelson product makes π*(ΩX) ⊗ 𝔽 into a graded Lie algebra denoted by LX;

  • (2)

    the Hurewicz homomorphism for ΩX is an isomorphism of LX onto the Lie algebra P*(ΩX; 𝔽) of primitive elements in H*(ΩX; 𝔽);

  • (3)

    the Hurewicz homomorphism extends to an isomorphism of graded Hopf algebras ULX≅H*(ΩX; 𝔽), where ULX is the universal enveloping algebra of LX.

It is natural to ask what are the rationally nontrivial indecomposable and decomposable generators of the graded Lie algebra for ΩΣBU(1)? The following gives an answer to this question.

Theorem 8. The connected graded Lie algebra for ΩΣBU(1) with the Samelson products modulo torsions is as follows:

()
where the dimension of   ξn is equal to 2n in the graded homotopy groups for each n = 1,2, 3, ….

Proof. It suffices to show that the iterated Samelson products in homotopy groups are rationally nontrivial decomposable generators, where the are indecomposable generators in dimension 2ij, for ij = 1,2, 3, … and k ≥ 2.

We first note that the Eckmann-Hilton dual of the Hopf-Thom theorem (see [11, pages 263–269] and [12, Chapter III]) says that ΣBU(1) has the rational homotopy type of the wedge products of infinitely many spheres; that is,

()

Let be the adjoint of . We prove the result in the case of twofold Samelson products. Suppose that is rationally trivial in . It follows by the adjointness and the Hilton’s formula that the twofold Whitehead products have a finite order in which is a subgroup of . By using a cofibration sequence

()
we have
()
where is the attaching map. The assumption shows that when is rationalized, and thus
()
where “≃ℚ” is a rational homotopy equivalence. We also have a contradiction by applying the cohomology cup products to the above rational homotopy equivalence.

For induction, we now suppose that the (k − 1)-fold Samelson products are rationally nontrivial in the homotopy group . By Theorem 3 and adjointness again, we can consider the iterated Whitehead product as a rational generator of

()

Similarly, a cofibration shows that

()
where is the attaching map. If this map has a finite order in homotopy groups, then we have a contradiction again by the same argument of the cohomology cup products.

Finally by taking the adjointness, we complete the proof.

Let be the composition r∘ξn of the rationally nontrivial indecomposable element ξn : S2n → ΩΣBU(1) of π2n(ΩΣBU(1)) with the rationalization r : ΩΣBU(1) → ΩΣBU(1) ℚ for each n = 1,2, …. Since there is a one-to-one correspondence between the integral generators of homotopy groups modulo torsions and rational generators of rational homotopy groups; that is, rankℤ(π2n+1(ΣBU(1))/torsion) = rankℚ(π2n+1(ΣBU(1)) ⊗ ℚ), by using the Milnor-Moore theorem and Theorem 8, we have the following.

Corollary 9. The graded rational homotopy group π*(ΩΣBU(1)) ⊗ ℚ with the Samelson products becomes a connected graded free Lie algebra generated by ; that is,

()

We note that the iterated Samelson products are decomposable generators in the above free Lie algebra.

It is well known that the Hurewicz homomorphism h : π*(ΩΣBU(1)) → H*(ΩΣBU(1); ℚ) carries the Samelson product into the Lie bracket defined by
()
where z, w ∈ H*(ΩΣBU(1); ℚ), and the multiplication is the Pontrjagin multiplication.

Theorem 10. Let be the adjoint of . Then one has the following:

  • (1)

    ;

  • (2)

    , where is a rational homology generator in dimension 2(i1 + i2), is the Lie bracket, and and are homotopy elements of π*(ΩΣBU(1)).

Proof. (1) The adjointness shows that, for F ∈ [ΣBU(1), ΣBU(1)], s ∈ BU(1), t ∈ I, and 〈s, t〉 ∈ ΣBU(1), the map

()
defined by
()
is a group isomorphism. It thus follows that
()
which is the commutator of and in [BU(1), ΩΣBU(1)].

(2) For the second part, if is the projection map to the top cell and if 〈, 〉 is the Samelson product in π*(ΩΣBU(1)), then the following diagram is commutative up to homotopy (see also [20, Theorem 1.4]):

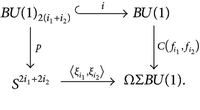
image

()

By applying the rational homology to the above diagram, we have

()

Here,

  • (i)

    is also used as a generator of

    ()

  • (ii)

    ;

  • (iii)

    ()
    is an isomorphism sending the generator to the fundamental homology class .

Theorem 11. Let E : BU(1) → ΩΣBU(1) be the canonical inclusion and let be the projection map. Then for a given commutator , there exists a map

()
such that .

Proof. We first show that the following diagram is strictly commutative:

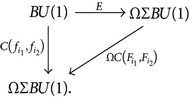
image

()

Indeed, the composition induces a map

()
sending t ∈ I to
()

On the other hand, sends s ∈ BU(1) to

()

By adjointness, we have

()
where 〈s, t〉 is an element of ΣBU(1). Therefore, we get
()

We now consider the cell structure on BU(1) × BU(1) with

()

Since the restrictions and are inessential from our construction of fn : BU(1) → ΩΣBU(1) for each n = 1,2, 3, …, we see that if m ≤ 2i1 − 1 or n ≤ 2i2 − 1, then is null homotopic. By using the homotopy extension property, we can extend the null homotopy to all of . Thus, by the cellular approximation theorem, we have

()
where Δ′ : BU(1) → BU(1) × BU(1) is a cellular map. Therefore there exists a map
()
such that the following diagram is commutative up to homotopy:

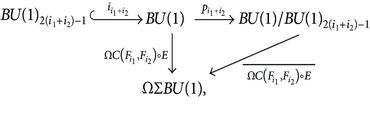
image

()
where the top row is a cofibration sequence as required.

The Milnor-Moore theorem asserts that the image of the Hurewicz homomorphism is primitive. The following is another expression of the primitive elements in the Pontrjagin algebra.

Theorem 12. The image of a homomorphism

()
is primitive for each n = 1,2, 3, ….

Proof. Since fn : BU(1) → ΩΣBU(1), n = 1,2, 3, … can be factored as

()
so that the restriction to the bottom sphere of the map coincides with the map ξn : S2n → ΩΣBU(1), and since BU(1)/BU(1) 2n−1 is (2n − 1)-connected, by the Hurewicz isomorphism theorem, every class in H2n(BU(1)/BU(1) 2n−1) is spherical, and thus primitive. We therefore know that the image of lies in the set of primitives P2n(ΩΣBU(1)) in H2n(ΩΣBU(1)), so does the image of for each n = 1,2, 3, ….

Since the restriction to the skeleton
()
is null homotopic, by Theorem 12, we have the following.

Corollary 13.

()
is in the Lie subalgebra P*(ΩΣBU(1); ℚ) of primitive elements in H*(ΩΣBU(1); ℚ).

Remark 14. We note that the self-map

()
is a loop map; thus it is an H-map. It is well known in [3, page 75] that there is a bijection between the groups [ΣBU(1), ΣBU(1)] and [ΩΣBU(1),ΩΣBU(1)]H of homotopy classes of H-maps ΩΣBU(1) → ΩΣBU(1). We thus get the corresponding self-map in the group [ΣBU(1), ΣBU(1)]. Moreover, by using the classical Whitehead theorem, we obtain a homotopy self-equivalence of the form ; that is, , where I is the identity map and “+” is the suspension addition on ΣBU(1).

Acknowledgments

The author is grateful to an anonymous referee for a careful reading and many helpful suggestions that improved the quality of the paper. This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2012-0007611).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.