Projective Lag Synchronization of Delayed Neural Networks Using Intermittent Linear State Feedback

Definition 1. The master system (2) and the slave system (4) are said to be projective lag synchronization if there exist a compact set α, σ and delay time θ such that, for any initial values φ(t₀), ψ(t₀) ∈ Ω, t₀ ∈ [−τ, 0], the error system is exponentially stable; that is,

Theorem 2. Suppose that there exist constants α, the coupling strength k, time delay θ, and the functions H(t), K(t) such that

• (i)

  C + C^T − 2kI + g₁I ≤ 0;

• (ii)

  C + C^T − g₂I ≤ 0;

• (iii)

  H(t) = −Af(y(t)) − Bg(y(t − τ)) + αAf(x(t − θ)) + αBg(x(t − τ − θ));

• (iv)

  K(t) = −k(y(t) − αx(t − θ));

• (v)

  g₁σ − (1 − σ)g₂ > 0.

Then, the projective lag synchronization error system (7) is globally exponentially stable, that is; the projective lag synchronization between the master system (2) and the slave system (4) under intermittent control (5) is achieved.

Proof. Consider the following Lyapunov function:

When nT ≤ t < nT + σT, the derivative of (9) with respect to time t along the trajectories of the first subsystem of the system (7) is calculated and estimated as follows:

Similarly, when nT + σT ≤ t < (n + 1)T, one obtains Therefore, Then, one observes that By (12) and (13), we can obtain the following.

(1) For 0 ≤ t < σT,

(2) For σT ≤ t < T,

(3) For T ≤ t < T + σT,

(4) For T + σT ≤ t < 2T,

By induction, we have the following.

(5) For nT ≤ t < nT + σT,

Note that (t − σT)/T ≤ n < t/T; in this case, we can obtain

(6) For nT + σT ≤ t < (n + 1)T

Note that t/T ≤ n + 1 < (t + T − σT)/T; in this case, we can obtain Therefore, for any t ≥ 0,

This implies that the projective lag synchronization error system (7) is globally exponentially stable, and the following estimate holds:

This implies that the projective lag synchronization between the master system (2) and slave system (4) is achieved.

Corollary 3. Suppose that there exist positive scalars k and σ satisfying 0 < σ < 1 such that

where $$ and $$. Then, the system (7) is exponentially stable, and the projective lag synchronization between the master system (2) and the slave system (4) under intermittent control (5) is achieved.

Remark 4. If α = 1, it is clear that the lag synchronization between the system (2) and system (4) will occur.

Remark 5. It is clear that when the time delay vanishes, that is, θ = 0, we have e(t) = y(t) − αx(t), which implies that the projective synchronization between master system (2) without delay and system (4) without delay will occur.

Remark 6. From Corollary 3, one observes that the control strength k can be estimated as follows:

Note that C are determined only by the system itself, and σ is control parameter. Then, we can estimate the feasible region D of control parameters (k, σ) as follows:

Example 1. Consider the Lu neural oscillator [17]

where and f(x(t)) = g(x(t)) = tanh(x(t)).

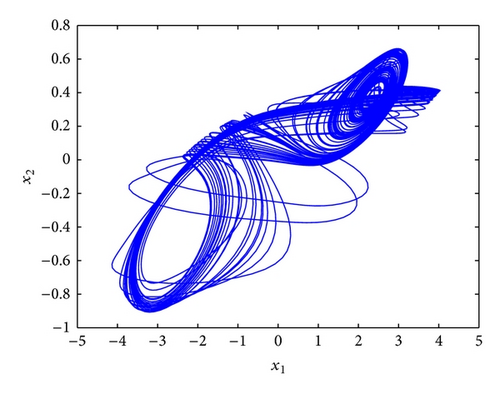
This model was investigated by Lu in [17] where it was shown to be chaotic, as shown in Figure 1. The corresponding slave system is given by

From Theorem 2, the controller can be obtained as follows:

So, when nT ≤ t < nT + σT, we have When nT + σT ≤ t < (n + 1)T, we have

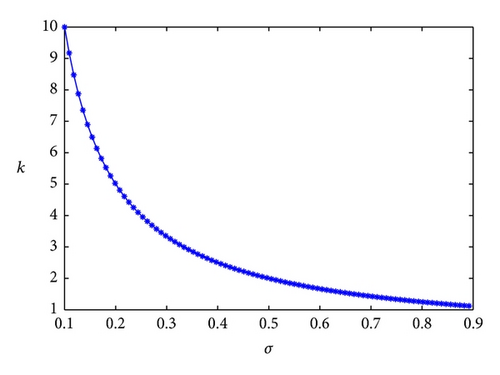
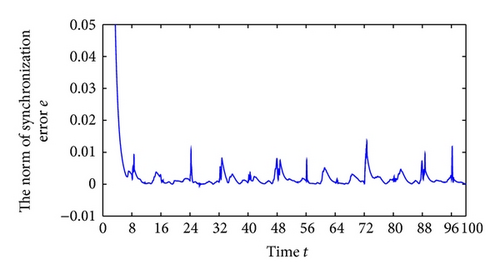
Noting that λ_max(C + C^T) = 2, the feasible region of control parameters (k, σ) is D = {(k, σ)∣k < k^* = −1/σ,  0 < σ < 1}, as shown in Figure 2. For numerical simulation, we select α = 2, θ = 0.01, σ = 0.1, and k = 10 and plot the norm of projective lag synchronization errors curve, as shown in Figure 3. As the time t goes to infinity, the projective lag synchronization error system is stable. Hence, the projective lag synchronization between system (27) and system (29) is achieved.