Abstract and Applied Analysis
Volume 2013, Issue 1 498457
Research Article
Open Access

Computing Eigenvalues of Discontinuous Sturm-Liouville Problems with Eigenparameter in All Boundary Conditions Using Hermite Approximation

M. M. Tharwat, 

M. M. Tharwat

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef 62511, Egypt bsu.edu.eg

Search for more papers by this author
A. H. Bhrawy, 

Corresponding Author

A. H. Bhrawy

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Beni-Suef University, Beni-Suef 62511, Egypt bsu.edu.eg

Search for more papers by this author
A. S. Alofi, 

A. S. Alofi

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Search for more papers by this author
First published: 29 August 2013
https://doi.org/10.1155/2013/498457
Citations: 2
Academic Editor: Jose L. Gracia

Abstract

The eigenvalues of discontinuous Sturm-Liouville problems which contain an eigenparameter appearing linearly in two boundary conditions and an internal point of discontinuity are computed using the derivative sampling theorem and Hermite interpolations methods. We use recently derived estimates for the truncation and amplitude errors to investigate the error analysis of the proposed methods for computing the eigenvalues of discontinuous Sturm-Liouville problems. Numerical results indicating the high accuracy and effectiveness of these algorithms are presented. Moreover, it is shown that the proposed methods are significantly more accurate than those based on the classical sinc method.

1. Introduction

The mathematical modeling of many practical problems in mechanics and other areas of mathematical physics requires solutions of boundary value problems (see, for instance, [1–7]). It is well known that many topics in mathematical physics require the investigation of the eigenvalues and eigenfunctions of Sturm-Liouville-type boundary value problems. The literature on computing eigenvalues of various types of Sturm-Liouville problems is little and we refer to [8–15].

Sampling theory is one of the most powerful results in signal analysis. It is of great need in signal processing to reconstruct (recover) a signal (function) from its values at a discrete sequence of points (samples). If this aim is achieved, then an analog (continuous) signal can be transformed into a digital (discrete) one and then it can be recovered by the receiver. If the signal is band-limited, the sampling process can be done via the celebrated Whittaker, Shannon, and Kotel’nikov (WSK) sampling theorem [16–18]. By a band-limited signal with band width σ, σ > 0, that is, the signal contains no frequencies higher than σ/2π cycles per second (cps), we mean a function in the Paley-Wiener space of the entire functions of the exponential type at most σ which are L2(ℝ)-functions when restricted to ℝ. Assume that . Then f(t) can be reconstructed via the Hermite-type sampling series
()
where Sn(t) is the sequences of sinc functions
()
Series (1) converges absolutely and uniformly on ℝ (cf. [19–22]). Sometimes, series (1) is called the derivative sampling theorem. Our task is to use formula (1) to compute the eigenvalues numerically of differential equation
()
with boundary conditions
()
()
and transmission conditions
()
where μ is a complex spectral parameter; q(x) is a given real-valued function, which is continuous in [−1,0) and (0,1] and has a finite limit ; γi, δi, αi, βi, , and (i = 1,2) are real numbers; γi ≠ 0, δi ≠ 0 (i = 1,2); γ1γ2 = δ1δ2; and
()
The eigenvalue problem (3)–(6) will be denoted by Π(q, α, β, α′, β′, γ, δ) when . It is a Sturm-Liouville problem which contains an eigenparameter μ in two boundary conditions, in addition to an internal point of discontinuity.
This approach is a fully new technique that uses the recently obtained estimates for the truncation and amplitude errors associated with (1) (cf. [23]). Both types of errors normally appear in numerical techniques that use interpolation procedures. In the following we summarize these estimates. The truncation error associated with (1) is defined to be
()
where fN(t) is the truncated series
()
It is proved in [23] that if and f(t) is sufficiently smooth in the sense that there exists k ∈ ℤ+ such that tkf(t) ∈ L2(ℝ), then, for t ∈ ℝ, |t | < Nπ/σ, we have
()
where the constants ℰk and ηk,σ are given by
()
The amplitude error occurs when approximate samples are used instead of the exact ones, which we cannot compute. It is defined to be
()
where and are approximate samples of f(nπ/σ) and f′(nπ/σ), respectively. Let us assume that the differences , , n ∈ ℤ, are bounded by a positive number ε; that is, . If satisfies the natural decay conditions
()
()
0 < α ≤ 1, then, for , we have [23]
()
where
()
and is the Euler-Mascheroni constant.
The classical [24] sampling theorem of WKS for is the series representation
()
where the convergence is absolute and uniform on ℝ and it is uniform on compact sets of ℂ (cf. [24–26]). Series (17), which is of Lagrange interpolation type, has been used to compute eigenvalues of second-order eigenvalue problems; see, for example, [8–13, 15, 27, 28].

The use of (17) in numerical analysis is known as the sinc method established by Stenger et al. (cf. [29–31]). In [9, 15, 28], the authors applied (17) and the regularized sinc method to compute eigenvalues of different boundary value problems with a derivation of the error estimates as given by [32, 33]. In [34], the authors used Hermite-type sampling series (1) to compute the eigenvalues of Dirac system with an internal point of discontinuity. In [14], Tharwat proved that Π(q, α, β, α′, β′, γ, δ) has a denumerable set of real and simple eigenvalues.

In [35], we compute the eigenvalues of the problem Π(q, α, β, α′, β′, γ, δ) numerically by using sinc-Gaussian technique. The main aim of the present work is to compute the eigenvalues of Π(q, α, β, α′, β′, γ, δ) numerically by using Hermite interpolations with an error analysis. This method is based on sampling theorem and Hermite interpolations but applied to regularized functions, hence avoiding any (multiple) integration and keeping the number of terms in the Cardinal series manageable. It has been demonstrated that the method is capable of delivering higher order estimates of the eigenvalues at a very low cost; see [34]. Also, in this work, by using computable error bounds we obtain eigenvalue enclosures in a simple way which not have been proven in [35].

Notice that due to Paley-Wiener’s theorem if and only if there is g(·) ∈ L2(−σ, σ) such that
()
Therefore ; that is, f′(t) also has an expansion of the form (17). However, f′(t) can be also obtained by term-by-term differentiation formula of (17)
()
(see [24, page 52] for convergence). Thus the use of Hermite interpolations will not cost any additional computational efforts since the samples f(nπ/σ) will be used to compute both f(t) and f′(t) according to (17) and (19), respectively.

In the next section, we derive the Hermite interpolation technique to compute the eigenvalues of Π(q, α, β, α′, β′, γ, δ) with error estimates. The last section contains three worked examples with comparisons accompanied by figures and numerics with Lagrange interpolation method.

2. Treatment of Π(q, α, β, α′, β′, γ, δ)

In this section we derive approximate values of the eigenvalues of Π(q, α, β, α′, β′, γ, δ). Recall that Π(q, α, β, α′, β′, γ, δ) has denumerable set of real and simple eigenvalues (cf. [14]). Let
()
denote the solution of (3) satisfying the following initial conditions:
()
Since y(·, μ) satisfies (4), (6), then the eigenvalues of problem (3)–(6) are the zeros of the characteristic determinant (cf. [14])
()
According to [14], see also [36–38], function Γ(μ) is an entire function of μ where zeros are real and simple. We aim to approximate Γ(μ) and hence its zeros, that is, the eigenvalues by the use of the sampling theorem. The idea is to split Γ(μ) into two parts: one is known and the other is unknown, but lies in a Paley-Wiener space. Then we approximate the unknown part using (1) to get the approximate Γ(μ) and then compute the approximate zeros. Using the method of variation of parameters, solution y(·, μ) satisfies the Volterra integral equations (cf. [14])
()
where 𝔗1 and 𝔗2 are the Volterra operators
()
Differentiating (23) we obtain
()
where and are the Volterra-type integral operators
()
Define ϑi(·, μ) and , i = 1,2, to be
()
In the following, we will make use of the known estimates:
()
where c0 is some constant (we may take c0≃1.72). For convenience, we define the constants
()
As in [15] we split Γ(μ) into two parts via
()
where 𝒢(μ) is the known part
()
and 𝒮(μ) is the unknown one
()
Then function 𝒮(μ) is entire in μ for each x ∈ [0,1] for which (cf. [15])
()
where
()
The analyticity of 𝒮(μ) as well as estimate (33) is not adequate to prove that 𝒮(μ) lies in a Paley-Wiener space. To solve this problem, we will multiply 𝒮(μ) by a regularization factor. Let θ ∈ (0,1) and m ∈ ℤ+, m > 5, be fixed. Let ℱθ,m(μ) be the function
()
The regularizing factor has been introduced in [9], in the context of the regularized sampling method, which was used in [9–13] to compute the eigenvalues of several classes of Sturm-Liouville problems. More specifications on m, θ will be given latter on. Then ℱθ,m(μ), see [15], is an entire function of μ which satisfies the estimate
()
Moreover, μm−5ℱθ,m(μ) ∈ L2(ℝ) and
()
where
()
What we have just proved is that ℱθ,m(μ) belongs to the Paley-Wiener space with σ = 2 + mθ. Since , then we can reconstruct the functions ℱθ,m(μ) via the following sampling formula:
()
Let N ∈ ℤ+, N > m, and approximate ℱθ,m(μ) by its truncated series ℱθ,m,N(μ), where
()
Since all eigenvalues are real, then from now on we restrict ourselves to μ ∈ ℝ. Since μm−5ℱθ,m(μ) ∈ L2(ℝ), the truncation error (cf. (10)) is given for |μ | < Nπ/σ by
()
where
()
The samples and , in general, are not known explicitly. So we approximate them by solving numerically 8N + 4 initial value problems at the nodes .
Let and be the approximations of the samples of and , respectively. Now we define , which approximates ℱθ,m,N(μ):
()
Using standard methods for solving initial problems, we may assume that for |n | < N
()
for a sufficiently small ε. From (36) we can see that ℱθ,m(μ) satisfies the condition (14) when m > 5, and therefore whenever we have
()
where there is a positive constant for which (cf. (15))
()
Here
()
In the following we use the technique of [27], see also [15], to determine enclosure intervals for the eigenvalues. Let μ* be an eigenvalue; that is,
()
Then it follows that
()
and so
()
Since
()
is given and
()
has computable upper bound, we can define an enclosure for μ*, by solving the following system of inequalities:
()
Its solution is an interval containing μ* over which the graph is squeezed between the graphs
()
Using the fact that
()
uniformly over any compact set, and since μ* is a simple root, we obtain for large N and sufficiently small ε
()
in a neighborhood of μ*. Hence the graph of
()
intersects the graphs
()
at two points with abscissae a−(μ*, N, ε) ≤ a+(μ*, N, ε), and the solution of the system of inequalities (53) is the interval
()
and in particular μ* ∈ Iε,N. Summarizing the above discussion, we arrive at the following lemma which is similar to that of [27] for Sturm-Liouville problems.

Lemma 1. For any eigenvalue μ*, one can find N0 ∈ ℤ+ and sufficiently small ε such that μ* ∈ Iε,N for N > N0. Moreover

()

Proof. Since all eigenvalues of Π(q, α, β, α′, β′, γ, δ) are simple, then for large N and sufficiently small ε we have , in a neighborhood of μ*. Choose N0 such that

()
has two distinct solutions which we denote by a−(μ*, N0, ε) ≤ a+(μ*, N0, ε). The decay of 𝒯N,m−5,σ(μ) → 0 as N → ∞ and 𝒜(ε) → 0 as ε → 0 will ensure the existence of the solutions a−(μ*, N, ε) and a+(μ*, N, ε) as N → ∞ and ε → 0. For the second point we recall that as N → ∞ and ε → 0. Hence by taking the limit we obtain
()
That is  Γ(a+) = Γ(a−) = 0. This leads us to conclude that a+ = a− = μ* since μ* is a simple root.

Let . Then (41) and (45) imply
()
and θ is chosen sufficiently small for which |θμ | < π. Therefore θ, m must be chosen so that for |μ | < Nπ/σ
()
Let μ* be an eigenvalue and let μN be its approximation. Thus Γ(μ*) = 0 and . From (63) we have . Now we estimate the error |μ* − μN| for an eigenvalue μ*.

Theorem 2. Let μ* be an eigenvalue of Π(q, α, β, α′, β′, γ, δ). For sufficiently large N one has the following estimate:

()

Proof. Since , then from (63) and after replacing μ by μN we obtain

()
Using the mean value theorem yields that for some ζ ∈ Jε,N∶ = [min (μ*, μN), max (μ*, μN)]
()
Since thlarge and we get (65).

3. Numerical Examples

This section includes three detailed worked examples illustrating the above technique. By ES and EH we mean the absolute errors associated with the results of the classical sinc method [9, 15] and our new method (Hermite interpolations), respectively. The first two examples are computed in [15] with the classical sinc method. We indicate in these two examples the effect of the amplitude error in the method by determining enclosure intervals for different values of ε. We also indicate the effect of the parameters m and θ by several choices. Also, ine eigenvalues are simple, then for sufficiently the following two examples, we observe that the exact solutions μk and the zeros of Γ(μ) are all inside the interval [a−, a+]. In the third example, we compare our new method with the classical sinc method [9]. We would like to mention that mathematica has been used to obtain the exact values for the two examples where eigenvalues cannot be computed concretely. mathematica is also used in rounding the exact eigenvalues, which are square roots. Both numerical results and the associated figures prove the credibility of the method.

Recall that a±(μ) are defined by
()
Recall also that the enclosure interval Iε,N∶ = [a−, a+] is determined by solving
()

Example 1. Consider the boundary value problem [15]

()
Here , , γ1 = δ1 = 2, γ2 = δ2 = 1/2, and
()
The characteristic function is
()
The function 𝒦(μ) will be
()

The application of Hermite interpolations method and sinc method [15] to this problem and the effect of θ and m at N = 20 are indicated in Tables 1 and 2. In Tables 3 and 4, we display the maximum absolute error of μk − μk,N, using Hermite interpolations method and sinc method [15] with various choices of θ and m at N = 20. From these tables, it is shown that the proposed methods are significantly more accurate than those based on the classical sinc method [15].

Table 1. Comparing the exact, sinc, and Hermite solutions at N = 20, m = 8, and θ = 1/6.
μk Sinc μk,N [15] Exact μk Hermite μk,N
μ1 0.5796031003909555 0.579603114810978 0.5796031148176034
μ2 1.7849838911323737 1.7849838948888357 1.7849838948886403
μ3 3.2386473557238586 3.238647349751419 3.238647349751933
μ4 4.7705623346546995 4.770562335590527 4.770562335590518
μ5 6.32570436013402 6.3257043646722515 6.325704364672412
Table 2. Comparing the exact, sinc, and Hermite solutions at N = 20, m = 12, and θ = 1/4.
μk Sinc μk,N [15] Exact μk Hermite μk,N
μ1 0.5796031148103449 0.57960311481097786078 0.57960311481097786304
μ2 1.7849838948900418 1.78498389488883561160 1.78498389488883560884
μ3 3.2386473497526262 3.23864734975141899542 3.23864734975141899687
μ4 4.77056233558413 4.77056233559052749760 4.77056233559052748750
μ5 6.325704364662005 6.32570436467225155153 6.32570436467225155387
Table 3. Absolute errors |μk − μk,N| for N = 20, m = 8, and θ = 1/6.
μk μ1 μ2 μ3 μ4 μ5
ES [15] 1.442 × 10−8  3.757 × 10−9   5.972  × 10−9 1 9.358 × 10−10  4.538 × 10−9 
EH 6.625 × 10−12  1.954 × 10−13  5.138 × 10−13 8.882 × 10−15  1.608 × 10−13 
Table 4. Absolute errors |μk − μk,N| for N = 20, m = 12, and θ = 1/4.
μk μ1 μ2 μ3 μ4 μ5
ES [15] 6.332 × 10−13  1.206 × 10−12  1.207 × 10−12 6.397 × 10−12  1.025 × 10−11 
EH 2.3 × 10−18  2.8 × 10−18  1.5 × 10−18 1.01 × 10−17  2.3 × 10−18 

Tables 5 and 6 list the exact solutions μk for two choices of m and θ at N = 20 and different values of ε. It is indicated that the solutions μk are all inside the interval [a−, a+] for all values of ε.

Table 5. For N = 20, m = 8, and θ = 1/6, the exact solutions μk are all inside the interval [a−, a+] for different values of ε.
μk Exact μk [a−, a+], ε = 10−5 [a−, a+], ε = 10−10
μ1 0.579603114810978 [0.504287, 0.644005] [0.579603, 0.581089]
μ2 1.7849838948888357 [1.76837, 1.80095] [1.78494, 1.78503]
μ3 3.238647349751419 [3.18936, 3.28517] [3.2375, 3.23979]
μ4 4.770562335590527 [4.74591, 4.79495] [4.77054, 4.77059]
μ5 6.3257043646722515 [6.30433, 6.34704] [6.32536, 6.32605]
  • ℰ3(ℱθ,m) = 2.61231 × 1011, ℰ2(ℱθ,m) = 4.67787 × 1010, α = 1, and .
Table 6. For N = 20, m = 12; and θ = 1/4, μk are all inside the interval [a−, a+] for different values of ε.
μk Exact μk [a−, a+], ε = 10−5 [a−, a+], ε = 10−10
μ1 0.57960311481097786078 [0.130168, 0.796074] [0.579579, 0.579627]
μ2 1.78498389488883561160 [1.699182, 1.859482] [1.784963, 1.785004]
μ3 3.23864734975141899542 [3.194355, 3.282835] [3.238636, 3.238658]
μ4 4.77056233559052749760 [4.698242, 4.851169] [4.770489, 4.770635]
μ5 6.32570436467225155153 [6.287476, 6.368771] [6.325701, 6.325707]
  • ℰ7(ℱθ,m) = 2.25863 × 1013, ℰ6(ℱθ,m) = 5.91004 × 1012, α = 1, and .

For N = 20, m = 8, and θ = 1/6, Figures 1 and 2 illustrate the enclosure intervals dominating μ1 for ε = 10−5 and ε = 10−10, respectively. The middle curve represents Γ(μ), while the upper and lower curves represent the curves of a+(μ), a−(μ), respectively. We notice that when ε = 10−10 all three curves are almost identical. Similarly, Figures 3 and 4 illustrate the enclosure intervals dominating μ2 for ε = 10−5, ε = 10−10, respectively.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 8, θ = 1/6, and ε = 10−5.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 8, θ = 1/6, and ε = 10−10.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 8, θ = 1/6, and ε = 10−5.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 8, θ = 1/6, and ε = 10−10.

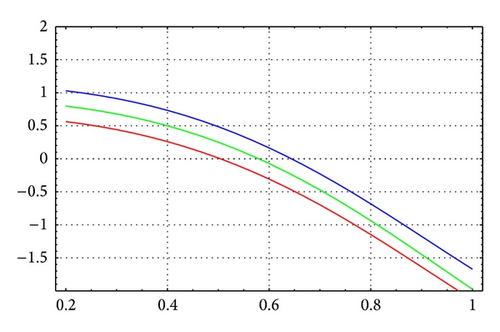
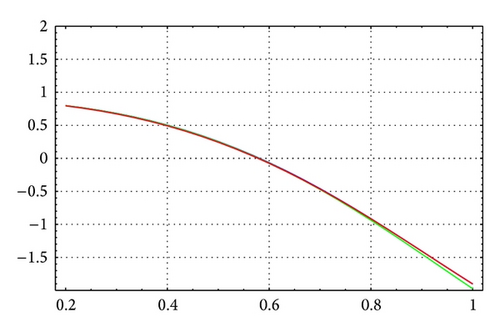
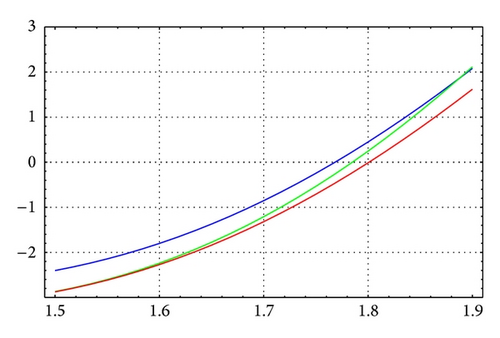
As in Table 6, for N = 20, m = 12, and θ = 1/4, Figures 5 and 6 illustrate the enclosure intervals dominating μ3 for ε = 10−5 and ε = 10−10, respectively, and Figures 7 and 8 illustrate the enclosure intervals dominating μ4 for ε = 10−5, ε = 10−10, respectively.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 12, θ = 1/4, and ε = 10−5.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 12, θ = 1/4, and ε = 10−10.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 12, θ = 1/4, and ε = 10−5.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 20, m = 12, θ = 1/4, and ε = 10−10.

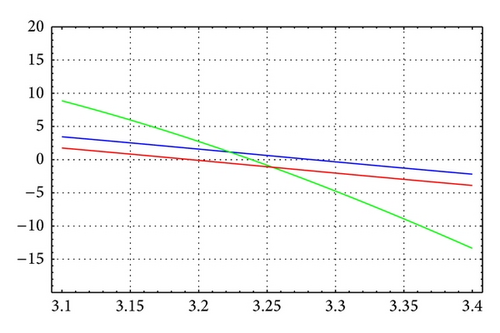
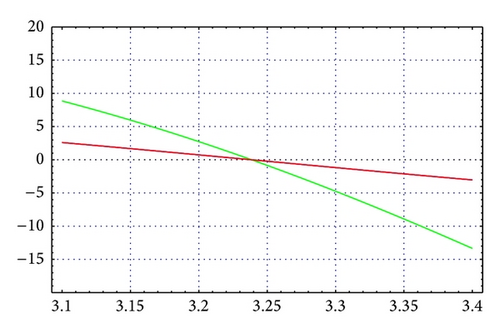
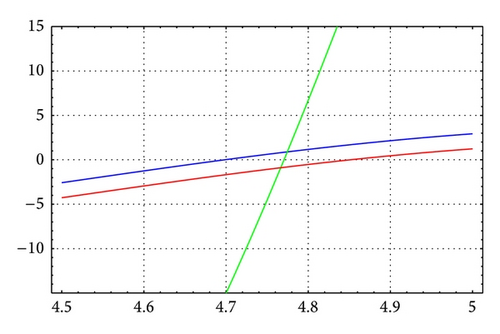
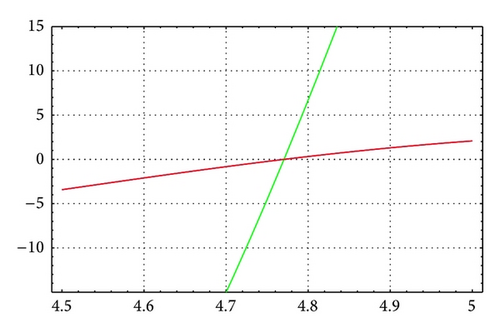
Example 2. Consider the boundary value problem

()
where α1 = β1 = 1, , , γ1 = δ1 = 3, γ2 = δ2 = 1/3, and
()
The function 𝒦(μ) will be
()

The application of Hermite interpolations method and sinc method [15] to this problem and the effect of θ and m at N = 40 are indicated in Tables 7 and 8. In Tables 9 and 10, we display the maximum absolute error of μk − μk,N, using Hermite interpolations method and sinc method [15] with various choices of θ and m at N = 40. Form these tables, it is shown that the proposed methods are significantly more accurate than those based on the classical sinc method [15].

Table 7. Comparing the exact, sinc, and Hermite solutions at N = 40, m = 12, and θ = 1/14.
μk Sinc μk,N [15] Exact μk Hermite μk,N
μ1 0.58718720635351373438 0.58718716772603949302 0.58718716772603439313
μ2 1.67733213643112965108 1.67733212404977904702 1.67733212404977962102
μ3 3.05318928070135885375 3.05318927948461569256 3.05318927948461567248
μ4 4.64836948022942956741 4.64836948049457049728 4.64836948049456789884
μ5 6.22695152015827473816 6.22695152029019996978 6.22695152029019996831
Table 8. Comparing the exact, sinc, and Hermite solutions at N = 40, m = 16, and θ = 1/12.
μk Sinc μk,N [15] Exact μk Hermite μk,N
μ1 0.58718716772553041066238963 0.58718716772603949302708573 0.58718716772603949300999675
μ2 1.67733212404966397991332993 1.67733212404977904702706192 1.67733212404977904702798867
μ3 3.05318927948463571892007113 3.05318927948461569256662121 3.05318927948461569256652760
μ4 4.648369480494569410072581778 4.64836948049456789592198501 4.64836948049456789592198641
μ5 6.22695152029019694414158617 6.2269515202901999697647050 6.226951520290199969764695999
Table 9. Absolute errors |μk − μk,N| for N = 40, m = 12, and θ = 1/14.
μk μ1 μ2 μ3 μ4 μ5
ES [15] 3.863 × 10−8  1.238 × 10−8   1.217  × 10−9 2.651 × 10−10  1.319 × 10−10 
EH 5.099 × 10−15   5.739 × 10−16  2.009 × 10−17 2.598 × 10−15  1.467 × 10−18 
Table 10. Absolute errors |μk − μk,N| for N = 40, m = 16, and θ = 1/12.
μk μ1 μ2 μ3 μ4 μ5
ES [15] 5.091 × 10−13  1.1506 × 10−13   2.003  × 10−14 1.514 × 10−15  3.025 × 10−15 
EH 1.708 × 10−20   9.267 × 10−22  9.361 × 10−23 1.403 × 10−24  9.010 × 10−24 

Tables 11 and 12 list the exact solutions μk for two choices of m and θ at N = 40 and different values of ε. It is indicated that the solutions μk are all inside the interval [a−, a+] for all values of ε.

Table 11. For N = 40, m = 12, and θ = 1/14, μk are all inside the interval [a−, a+] for different values of ε.
μk Exact μk [a−, a+], ε = 10−6 [a−, a+], ε = 10−12
μ1 0.58718716772603949302 [0.477526, 0.667764] [0.586774, 0.587599]
μ2 1.67733212404977904702 [1.666867, 1.687341] [1.677285, 1.677378]
μ3 3.05318927948461569256 [3.046882, 3.059372] [3.053187, 3.053190]
μ4 4.64836948049457049728 [4.647491, 4.649246] [4.64836924, 4.64836971]
μ5 6.22695152029019996978 [6.226707, 6.227195] [6.22695140, 6.22695163]
  • ℰ7(ℱθ,m) = 6.29794 × 1019, ℰ6(ℱθ,m) = 4.70791 × 1018, α = 1, and .
Table 12. For N = 40, m = 16, and θ = 1/12, μk are all inside the interval [a−, a+] for different values of ε.
μk Exact μk [a−, a+], ε = 10−7 [a−, a+], ε = 10−12
μ1 0.58718716772603949302708573 [0.554227, 0.616993] [0.587165, 0.587209]
μ2 1.67733212404977904702706192 [1.648191, 1.703225] [1.6773305, 1.6773337]
μ3 3.05318927948461569256662121 [3.050775, 3.055585] [3.05318912, 3.05318943]
μ4 4.64836948049456789592198501 [4.647994, 4.648743] [4.648369468, 4.648369492]
μ5 6.2269515202901999697647050 [6.226831, 6.227072] [6.226951509, 6.226951531]
  • ℰ11(ℱθ,m) = 1.67235 × 1024, ℰ10(ℱθ,m) = 1.44089 × 1023, α = 1, and .

For N = 40, m = 12, and θ = 1/14, Figures 9 and 10 illustrate the enclosure intervals dominating μ1 for ε = 10−6 and ε = 10−12, respectively. Similarly, Figures 11 and 12 illustrate the enclosure intervals dominating μ2 for ε = 10−6, ε = 10−12, respectively.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 12, θ = 1/14, and ε = 10−6.
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 12, θ = 1/14, and ε = 10−12.
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
a+,  Γ(μ), and a− with N = 40, m = 12, θ = 1/14, and ε = 10−6.
Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 12, θ = 1/14, and ε = 10−12.

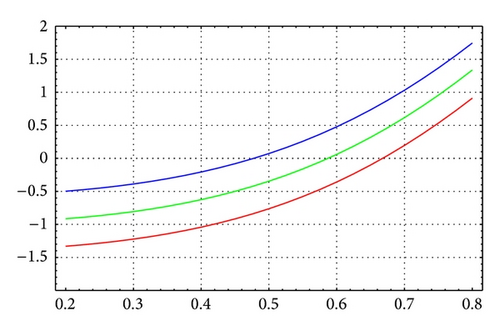
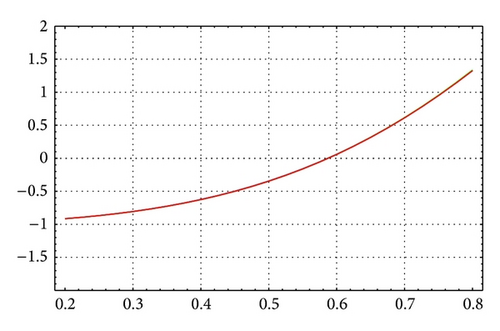
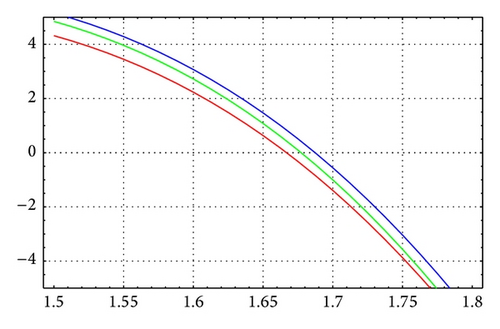
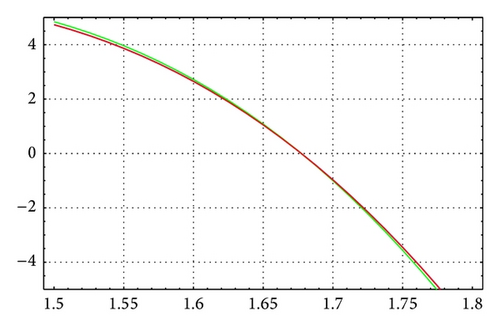
For N = 40, m = 16, and θ = 1/12, Figures 13 and 14 illustrate the enclosure intervals dominating μ1 for ε = 10−7 and ε = 10−12, respectively, and Figures 15 and 16 illustrate the enclosure intervals dominating μ2 for ε = 10−7, ε = 10−12, respectively.

Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 16, θ = 1/12, and ε = 10−7.
Details are in the caption following the image
Figure 14
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 16, θ = 1/12, and ε = 10−12.
Details are in the caption following the image
Figure 15
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 16, θ = 1/12, and ε = 10−7.
Details are in the caption following the image
Figure 16
Open in figure viewerPowerPoint
a+, Γ(μ), and a− with N = 40, m = 16, θ = 1/12, and ε = 10−12.

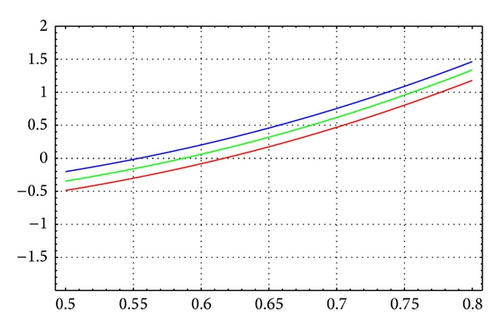
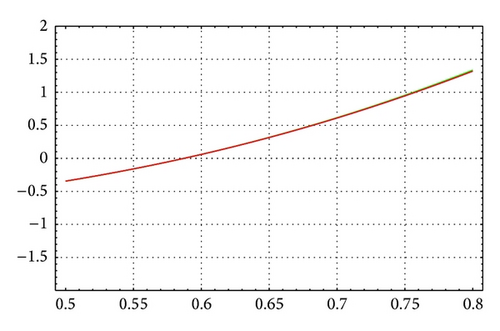
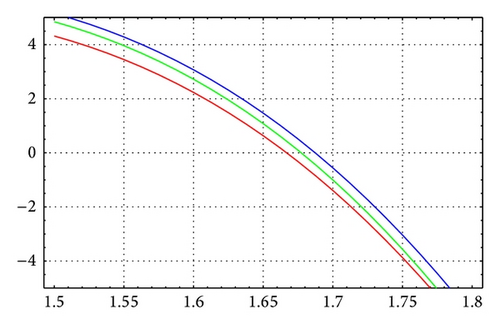
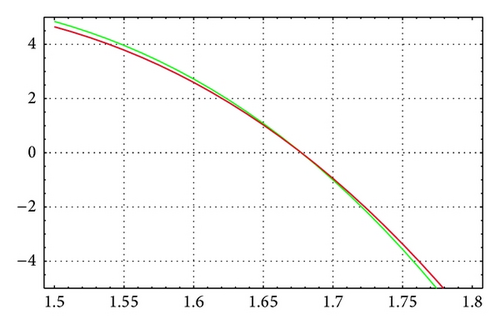
Example 3. Consider the continuous boundary value problem [9]

()
where d = −4π2, , α2 = d, , α2 = d, and . The exact characteristic function is
()
where zero is not an eigenvalue. The application of Hermite interpolations method and sinc method [9] to this problem is indicated in Table 13. From this table, it is shown that the proposed method is significantly more accurate than that based on the sinc method [9].

Table 13. Comparing the exact, sinc, and Hermite solutions at N = 40, m = 2.
μk Sinc μk,N [9] Exact μk Hermite μk,N ES EH
μ1 3.119437080035764 3.1194369008225 3.1194368826279857 1.79213 × 10−7 1.81945 × 10−8
μ2 9.421424381799804 9.421428536270897 9.421428567680044 4.15447 × 10−6 3.14091 × 10−8
μ3 12.565198874263179 12.565194405126995 12.56519440514131 4.46914 × 10−6 1.43157 × 10−11

Acknowledgments

This work was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant no. 130-065-D1433. The authors, therefore, acknowledge with thanks DSR technical and financial support.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.