This paper is concerned with a semiratio-dependent predator-prey system with nonmonotonic functional response and two delays. It is shown that the positive equilibrium of the system is locally asymptotically stable when the time delay is small enough. Change of stability of the positive equilibrium will cause bifurcating periodic solutions as the time delay passes through a sequence of critical values. The properties of Hopf bifurcation such as direction and stability are determined by using the normal form method and center manifold theorem. Numerical simulations confirm our theoretical findings.

1. Introduction

It is well known that there are many factors which can affect dynamical properties of predator-prey systems. One of the important factors is the functional response describing the number of prey consumed per predator per unit time for given quantities of prey and predators. Numerous laboratory experiment, and observations have shown that a more suitable general predator-prey system should be based on the “ratio-dependent” theory, especially when predators have to search, share, or compete for food [1–3]. And ratio-dependent predator-prey systems have been investigated by many scholars [4–11]. In [4], Zhang and Lu considered the following semi-ratio-dependent predator-prey system with the nonmonotonic functional response

()

where x₁(t) and x₂(t) denote the densities of the prey and the predator, respectively. r₁(t) and r₂(t) denote the intrinsic growth rates of the prey and the predator, respectively. b₁(t) is the intraspecific competition rate of the prey. a₁(t) is the capturing rate of the predator. a₂(t) is a measure of the food quality that the prey provided for conversion into predator birth. The predator grows logistically with the carrying capacity x₁(t)/a₂(t) proportional to the population size of the prey.

m ≠ 0, n ≥ 0, and a_i(t), r_i(t), b₁(t), (i = 1,2) are assumed to be continuously positive periodic functions with period ω. Zhang and Lu [4] established the existence of positive periodic solutions of system (1), and sufficient conditions for the uniqueness and global stability of the positive solutions of system (1) were also obtained by constructing a Lyapunov function.

Time delays of one type or another have been incorporated into predator-prey systems by many researchers since a time delay could cause a stable equilibrium to become unstable and cause the population to fluctuate [5, 6, 12–15]. In [5], Ding et al. incorporated the time delay τ(t) ≥ 0 due to negative feedback of the prey into system (1) and got the special case (n = 0) of system (1) with time delay

()

Ding et al. [5] established the existence of a positive periodic solution for system (2) by using the continuation theorem of coincidence degree theory. Sufficient conditions for the permanence of system (2) were obtained by Li and Yang in [6]. But studies on predator-prey systems not only involve the persistence and the periodic phenomenon but also involve many patterns of other behavior such as global attractivity [16, 17] and bifurcation phenomenon [18–21]. Starting from this point, we will study the bifurcation phenomenon and the properties of periodic solutions of the following predator-prey system with two delays:

()

Unlike the assumptions in [4–6], we assume that all the parameters of system (3) are positive constants. τ₁ ≥ 0 and τ₂ ≥ 0 are the feedback delays of the prey and the predator, respectively.

The rest of this paper is organized as follows. In Section 2, sufficient conditions are obtained for the local stability of the positive equilibrium and the existence of Hopf bifurcation for possible combinations of the two delays in system (3). In Section 3, we give the formula determining the direction of Hopf bifurcation and the stability of the bifurcating periodic solutions. Finally, numerical simulations supporting the theoretical analysis are also included.

2. Stability of the Positive Equilibrium and Local Hopf Bifurcations

It is not difficult to verify that system (2) has at least one positive equilibrium

, where

and

is the root of (4)

()

Let

. Dropping the bars for the sake of simplicity, system (2) can be rewritten in the following system:

()

where

()

The linearized system of (5) is

()

The associated characteristic equation of system (7) is

()

where

()

Case 1 (τ1 = τ2 = 0). Equation (8) becomes

()

All the roots of (10) have negative real parts if and only if

(H₁) A + B + C > 0 and D + E > 0.

Thus, the positive equilibrium

is locally stable when the condition (H₁) holds.

Case 2 (τ1 > 0, τ2 = 0). Equation (8) becomes

()

Let λ = iω₁ (ω₁ > 0) be the root of (11), and we have

()

It follows that

()

If condition (H₂)D − E < 0 holds, then (13) has only one positive root

()

Now, we can get the critical value of τ₁ by substituting ω₁₀ into (12). After computing, we obtain

()

Then, when τ = τ_1k, the characteristic equation (11) has a pair of purely imaginary roots ±iω₀.

Next, we will verify the transversality condition. Differentiating (11) with respect to τ₁, we get

()

Thus,

()

Obviously, if condition (H₂) holds, then

. Note that

Therefore, if condition (H₂) holds, the transversality condition is satisfied. From the analysis above, we have the following results.

Theorem 1. If conditions (H₁) and (H₂) hold, then the positive equilibrium of system (3) is asymptotically stable for τ₁ ∈ [0, τ₁₀) and unstable when τ₁ > τ₁₀. System (3) undergoes a Hopf bifurcation at the positive equilibrium when τ₁ = τ₁₀.

Case 3 (τ1 = 0, τ2 > 0). Equation (8) becomes

()

Let λ = iω₂ (ω₂ > 0) be the root of (18), and then we have

()

which leads to

()

Obviously, if the condition (H₁) holds, and then (20) has only one positive root

()

The corresponding critical value of τ₂ is

()

Similar to Case 2, differentiating (18) with respect to τ₂, we get

()

Then we can get

()

Obviously, if condition (H₁) holds, then . Namely, if condition (H₁) holds, then the transversality condition is satisfied. Thus, we have the following results.

Theorem 2. If condition (H₁) holds, then the positive equilibrium of system (3) is asymptotically stable for τ₂ ∈ [0, τ₂₀) and unstable when τ₂ > τ₂₀. System (3) undergoes a Hopf bifurcation at the positive equilibrium when τ₂ = τ₂₀.

Case 4 (τ1 = τ2 = τ > 0). Equation (8) can be transformed into the following form:

()

Multiplying e^λτ on both sides of (25), we get

()

Let λ = iω (ω > 0) be the root of (26), then we obtain

()

which follows that

()

Then, we have

()

where

()

Denote ω² = v, and then (29) becomes

()

Next, we give the following assumption.

(H₃) Equation (31) has at least one positive real root.

Suppose that (H₃) holds. Without loss of generality, we assume that (31) has four real positive roots, which are denoted by v₁, v₂, v₃, and v₄. Then (29) has four positive roots , k = 1,2, 3,4.

For every fixed ω_k, the corresponding critical value of time delay is

()

Let

()

Taking the derivative of λ with respect to τ in (26), we obtain

()

Thus,

()

with

()

It is easy to see that if condition (H₄)P_RQ_R + P_IQ_I ≠ 0, then . Therefore, we have the following results.

Theorem 3. If conditions (H₁) and (H₄) holds, then the positive equilibrium of system (3) is asymptotically stable for τ ∈ [0, τ₀) and unstable when τ > τ₀. System (3) undergoes a Hopf bifurcation at the positive equilibrium when τ = τ₀.

Case 5 (τ1 ≠ τ2, τ1 > 0 and τ2 > 0). Considered the following:

()

We consider (8) with τ₂ in its stable interval and regard τ₁ as a parameter.

Let () be the root of (8), and then we can obtain

()

Then we get

()

Define

()

If condition (H₁) D + E > 0 and (H₂) D − E < 0 hold, then F(0) = D² − E² < 0. In addition, F(+∞) = +∞. Therefore, (39) has at least one positive root. We suppose that the positive roots of (39) are denoted as . For every fixed , the corresponding critical value of time delay

()

with

()

Let

, i = 1,2, 3, …k. When τ₁ = τ_1*, (8) has a pair of purely imaginary roots ±iω_1* for τ₂ ∈ (0, τ₂₀).

Next, in order to give the main results, we give the following assumption

(H₅) .

Therefore, we have the following results on the stability and bifurcation in system (3).

Theorem 4. If the conditions (H₁) and (H₅) hold and τ₂ ∈ (0, τ₂₀), then the positive equilibrium of system (3) is asymptotically stable for τ₁ ∈ [0, τ_1*) and unstable when τ₁ > τ_1*. System (3) undergoes a Hopf bifurcation at the positive equilibrium when τ₁ = τ_1*.

3. Direction and Stability of the Hopf Bifurcation

In this section, we will investigate the direction of Hopf bifurcation and stability of the bifurcating periodic solutions of system (3) with respect to τ₁ for τ₂ ∈ (0, τ₂₀). We assume that τ_2* < τ_1* where τ_2* ∈ (0, τ₂₀).

Let τ₁ = τ_1* + μ, μ ∈ R so that μ = 0 is the Hopf bifurcation value of system (3). Rescale the time delay by t → (t/τ₁). Let

, and then system (3) can be rewritten as an PDE in C = C([−1,0], R²) as

()

where

()

are given, respectively, by

()

with

()

By the Riesz representation theorem, there is a 2 × 2 matrix function with bounded variation components η(θ, μ), θ ∈ [−1,0] such that

()

In fact, we have chosen

()

For ϕ ∈ C([−1,0]), R², we define

()

Then system (43) is equivalent to the following operator equation:

()

where u_t = u(t + θ) for θ ∈ [−1,0].

For φ ∈ C([−1,0]), (R²) ^*, we define the adjoint operator A^* of A as

()

and a bilinear inner product

()

where η(θ) = η(θ, 0).

Then, A(0) and A^*(0) are adjoint operators. From the discussion above, we can know that ±iω_1*τ_1* are the eigenvalues of A(0) and they are also eigenvalues of A^*(0).

Let

be the eigenvector of A(0) corresponding to iω_1*τ_1*, and q^*(θ) =

be the eigenvector of A^*(0) corresponding to −iω_1*τ_1*. Then we have

()

By a simple computation, we can get

()

Then,

()

Following the algorithms explained in the work of Hassard et al. [22] and using a computation process similar to that in [18], we can get the following coefficients which can determine the properties of Hopf bifurcation:

()

with

()

where E₁ and E₂ can be determined by the following equations, respectively:

()

with

()

Then, we can get the following coefficients:

()

In conclusion, we have the following results.

Theorem 5. If μ₂ > 0 (μ₂ < 0), then the Hopf bifurcation is supercritical (subcritical); if β₂ < 0 (β₂ > 0), then the bifurcating periodic solutions are stable (unstable); if T₂ > 0 (T₂ < 0), then the period of the bifurcating periodic solutions increases (decreases).

4. Numerical Simulation and Discussions

To demonstrate the algorithm for determining the existence of Hopf bifurcation in Section 2 and the properties of Hopf bifurcation in Section 3, we give an example of system (3) in the following form:

()

which has a positive equilibrium E^*(3.8298,7.6596). By calculation, we have A + B + C = 6.5788, D + E = 11.2470, and D − E = −11.7318. Namely, conditions (H₁) and (H₂) hold.

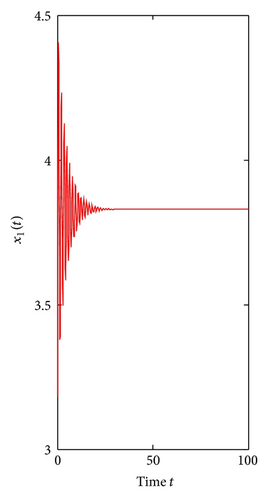
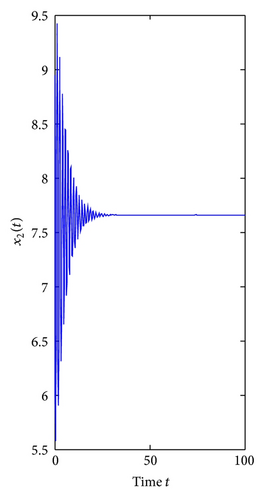
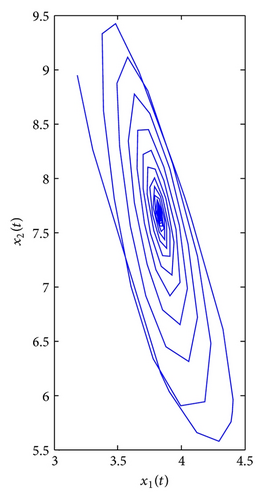
For τ₁ > 0, τ₂ = 0. We can get ω₁₀ = 3.9074, τ₁₀ = 0.3788. By Theorem 1, we know that when τ₁ ∈ [0, τ₁₀), the positive equilibrium E^*(3.8298,7.6596) is locally asymptotically stable and is unstable if τ₁ > τ₁₀. As can be seen from Figure 1, when we let τ₁ = 0.35 ∈ [0, τ₁₀), the positive equilibrium E^*(3.8298,7.6596) is locally asymptotically stable. However, when τ₁ = 0.395 > τ₁₀, the positive equilibrium E^*(3.8298,7.6596) is unstable and a Hopf bifurcation occurs and a family of periodic solutions bifurcate from the positive equilibrium E^*(3.8298,7.6596), which can be illustrated by Figure 2. Similarly, we can get ω₂₀ = 3.0827, τ₂₀ = 0.4912. The corresponding waveform and the phase plots are shown in Figures 3 and 4.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

E^* is asymptotically stable for τ₁ = 0.350 < τ₁₀ = 0.3788.

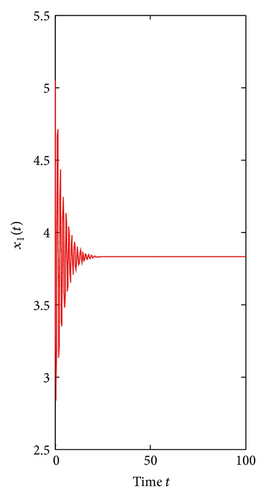
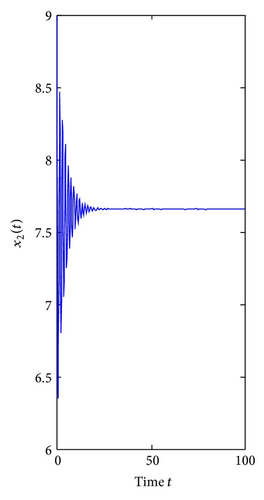
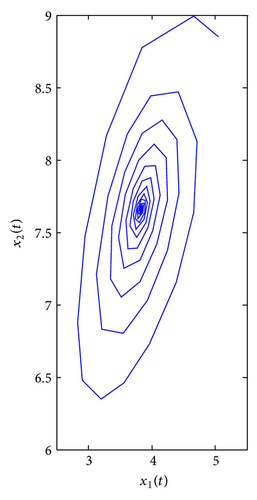
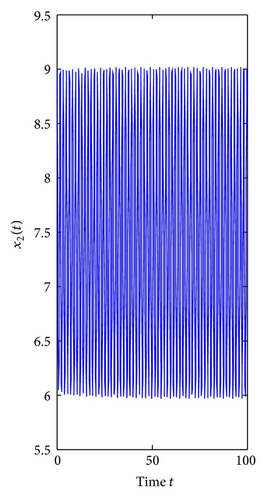
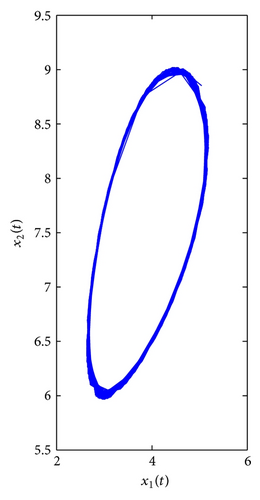
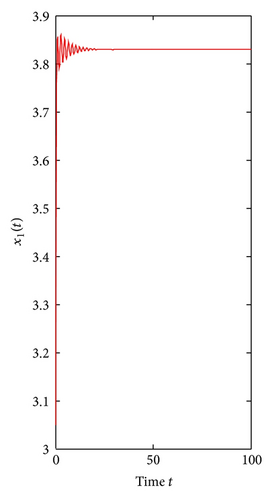
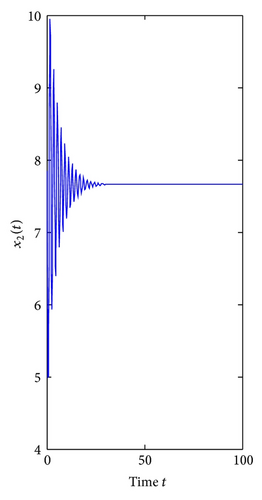
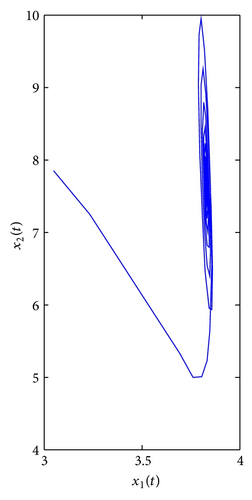
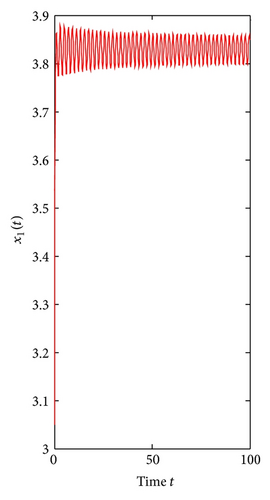
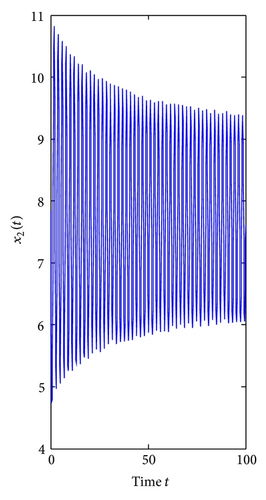
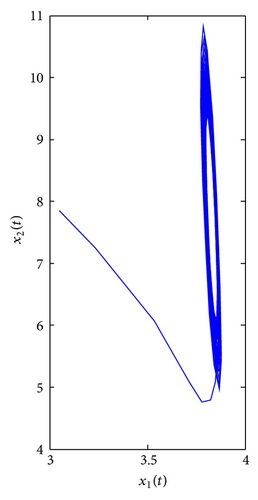
For τ₁ = τ₂ = τ > 0. We can obtain ω₀ = 3.4601, τ₀ = 0.3361. By Theorem 3, we know that when the time delay τ increases from zero to the critical value τ₀ = 0.3361, the positive equilibrium E^*(3.8298,7.6596) is locally asymptotically stable. It will lose its stability and a Hopf bifurcation occurs once τ > τ₀ = 0.3361. This property can be illustrated by Figures 5 and 6.

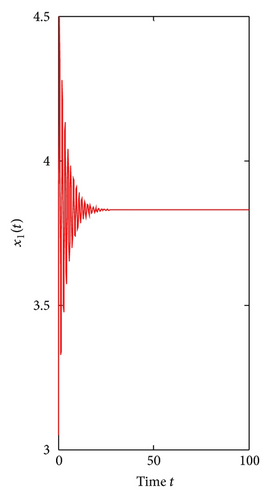
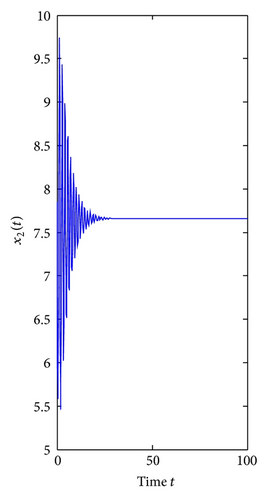
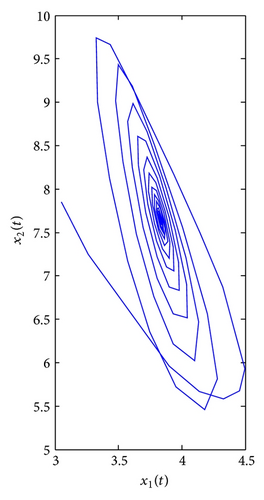
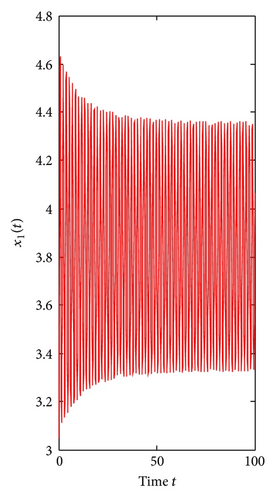
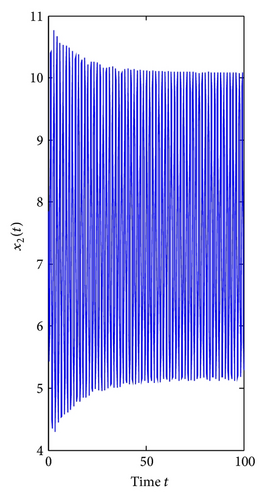
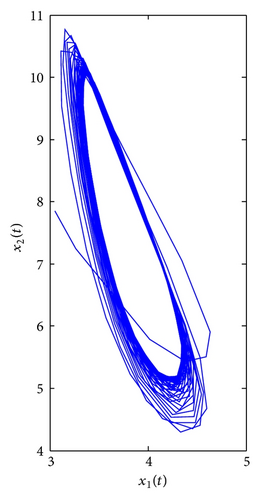
Finally, consider τ₁ as a parameter and let τ₂ = 0.3 ∈ (0, τ₂₀). We can get ω_1* = 2.3761, τ_1* = 0.3490, λ^′(τ_1*) = 8.2230 + 2.6054i. From Theorem 4, the positive equilibrium E^*(3.8298,7.6596) is locally asymptotically stable for τ₁ ∈ [0,0.3490) and unstable when τ₁ > τ_1* = 0.3490, which can be seen from Figures 7 and 8.

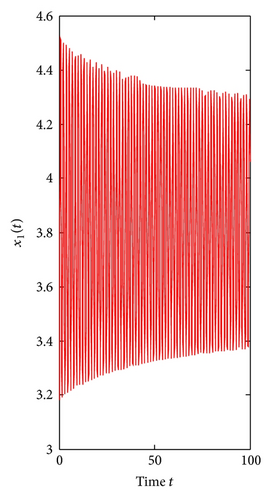
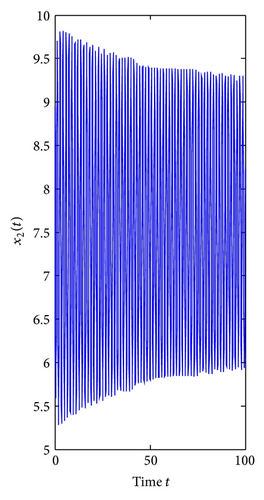
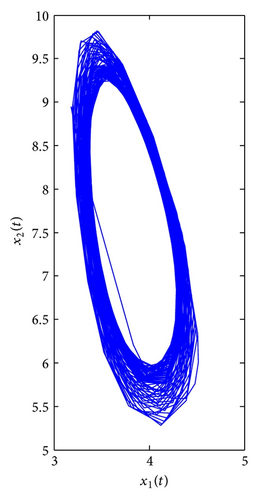
In addition, from (60), we can get C₁(0) = −41.5020 − 17.8366i. Furthermore, we have μ₂ = 5.0471 > 0, β₂ = −83.0040 < 0, T₂ = 5.6519 > 0. Therefore, from Theorem 5, we know that the Hopf bifurcation is supercritical. The bifurcating periodic solutions are stable and increase. If the bifurcating periodic solutions are stable, then the prey and the predator may coexist in an oscillatory mode. Therefore, the two species in system (3) may coexist in an oscillatory mode under certain conditions.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Arditi R. and Ginzburg L. R., Coupling in predator-prey dynamics: ratio-dependence, Journal of Theoretical Biology. (1989) 139, no. 3, 311–326, 2-s2.0-4944258042.
10.1016/S0022-5193(89)80211-5
Web of Science® Google Scholar
2 Arditi R., Perrin N., and Saiah H., Functional responses and heterogeneities: an experimental test with cladocerans, Oikos. (1991) 60, no. 1, 69–75, 2-s2.0-0025946035.
10.2307/3544994
Web of Science® Google Scholar
3 Hanski I., The functional response of predators: worries about scale, Trends in Ecology and Evolution. (1991) 6, no. 5, 141–142, 2-s2.0-0001397558.
10.1016/0169-5347(91)90052-Y
Web of Science® Google Scholar
4 Zhang L. and Lu C., Periodic solutions for a semi-ratio-dependent predator-prey system with Holling IV functional response, Journal of Applied Mathematics and Computing. (2010) 32, no. 2, 465–477, https://doi.org/10.1007/s12190-009-0264-3, MR2595858, ZBL1201.34073.
10.1007/s12190-009-0264-3
Google Scholar
5 Ding X., Lu C., and Liu M., Periodic solutions for a semi-ratio-dependent predator-prey system with nonmonotonic functional response and time delay, Nonlinear Analysis: Real World Applications. (2008) 9, no. 3, 762–775, https://doi.org/10.1016/j.nonrwa.2006.12.008, MR2392373, ZBL1152.34046.
10.1016/j.nonrwa.2006.12.008
Web of Science® Google Scholar
6 Li X. and Yang W., Permanence of a semi-ratio-dependent predator-prey system with nonmonotonic functional response and time delay, Abstract and Applied Analysis. (2009) 2009, 6, 960823, https://doi.org/10.1155/2009/960823, MR2539907, ZBL1182.34100.
10.1155/2009/960823
Google Scholar
7 Sen M., Banerjee M., and Morozov A., Bifurcation analysis of a ratio-dependent prey-predator model with the Allee effect, Ecological Complexity. (2012) 11, 12–27, 2-s2.0-84857301708, https://doi.org/10.1016/j.ecocom.2012.01.002.
10.1016/j.ecocom.2012.01.002
Web of Science® Google Scholar
8 Ding X. and Zhao G., Periodic solutions for a semi-ratio-dependent predator-prey system with delays on time scales, Discrete Dynamics in Nature and Society. (2012) 2012, 15, 928704, https://doi.org/10.1155/2012/928704, MR2948184, ZBL1248.34140.
10.1155/2012/928704
Web of Science® Google Scholar
9 Yang B., Pattern formation in a diffusive ratio-dependent Holling-Tanner predator-prey model with Smith growth, Discrete Dynamics in Nature and Society. (2013) 2013, 8, 454209, https://doi.org/10.1155/2013/454209, MR3037774, ZBL1264.34169.
10.1155/2013/454209
Web of Science® Google Scholar
10 Yue Z. and Wang W., Qualitative analysis of a diffusive ratio-dependent Holling-Tanner predator-prey model with Smith growth, Discrete Dynamics in Nature and Society. (2013) 2013, 9, 267173, https://doi.org/10.1155/2013/267173, MR3037767, ZBL1264.34170.
10.1155/2013/267173
Web of Science® Google Scholar
11 Haque M., Ratio-dependent predator-prey models of interacting populations, Bulletin of Mathematical Biology. (2009) 71, no. 2, 430–452, https://doi.org/10.1007/s11538-008-9368-4, MR2471054, ZBL1170.92027.
10.1007/s11538-008-9368-4
PubMed Web of Science® Google Scholar
12 Ferrara M. and Guerrini L., Center manifold analysis for a delayed model with classical saving, Far East Journal of Mathematical Sciences. (2012) 70, no. 2, 261–269, MR3051529, ZBL1267.34126.
Google Scholar
13 Guo S. and Jiang W., Hopf bifurcation analysis on general Gause-type predator-prey models with delay, Abstract and Applied Analysis. (2012) 2012, 17, 363051, https://doi.org/10.1155/2012/363051, MR2898048, ZBL1246.37095.
10.1155/2012/363051
Google Scholar
14 Wang C. Y., Wang S., Yang F. P., and Li L. R., Global asymptotic stability of positive equilibrium of three-species Lotka-Volterra mutualism models with diffusion and delay effects, Applied Mathematical Modelling. (2010) 34, no. 12, 4278–4288, https://doi.org/10.1016/j.apm.2010.05.003, MR2659674, ZBL1201.35030.
10.1016/j.apm.2010.05.003
Web of Science® Google Scholar
15 Ferrara M., Guerrini L., and Mavilia R., Modified neoclassical growth models with delay: a critical survey and perspectives, Applied Mathematical Sciences. (2013) 7, 4249–4257.
10.12988/ams.2013.36318
Google Scholar
16 Jiao J. J., Chen L. S., and Nieto J. J., Permanence and global attractivity of stage-structured predator-prey model with continuous harvesting on predator and impulsive stocking on prey, Applied Mathematics and Mechanics. (2008) 29, no. 5, 653–663, https://doi.org/10.1007/s10483-008-0509-x, MR2414687, ZBL1231.34021.
10.1007/s10483-008-0509-x
Google Scholar
17 Zhu Y. and Wang K., Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Leslie-Gower Holling-type II schemes, Journal of Mathematical Analysis and Applications. (2011) 384, no. 2, 400–408, https://doi.org/10.1016/j.jmaa.2011.05.081, MR2825193, ZBL1232.34077.
10.1016/j.jmaa.2011.05.081
Web of Science® Google Scholar
18 Ferrara M., Guerrini L., and Bianca C., The Cai model with time delay: existence of periodic solutions and asymptotic analysis, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 21–27, https://doi.org/10.12785/amis/070103, MR2998481.
10.12785/amis/070103
Google Scholar
19 Etoua R. M. and Rousseau C., Bifurcation analysis of a generalized Gause model with prey harvesting and a generalized Holling response function of type III, Journal of Differential Equations. (2010) 249, no. 9, 2316–2356, https://doi.org/10.1016/j.jde.2010.06.021, MR2718660, ZBL1217.34080.
10.1016/j.jde.2010.06.021
Web of Science® Google Scholar
20 Yang Y., Hopf bifurcation in a two-competitor, one-prey system with time delay, Applied Mathematics and Computation. (2009) 214, no. 1, 228–235, https://doi.org/10.1016/j.amc.2009.03.078, MR2541062, ZBL1181.34090.
10.1016/j.amc.2009.03.078
Web of Science® Google Scholar
21 Qu Y. and Wei J., Bifurcation analysis in a time-delay model for prey-predator growth with stage-structure, Nonlinear Dynamics. (2007) 49, no. 1-2, 285–294, https://doi.org/10.1007/s11071-006-9133-x, MR2325300, ZBL1176.92056.
10.1007/s11071-006-9133-x
Web of Science® Google Scholar
22 Hassard B. D., Kazarinoff N. D., and Wan Y. H., Theory and Applications of Hopf Bifurcation, 1981, Cambridge University Press, Cambridge, UK.
Google Scholar

Citing Literature

All articles

Hopf Bifurcation Analysis for a Semiratio-Dependent Predator-Prey System with Two Delays

Abstract

1. Introduction

2. Stability of the Positive Equilibrium and Local Hopf Bifurcations

3. Direction and Stability of the Hopf Bifurcation

4. Numerical Simulation and Discussions

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Hopf Bifurcation Analysis for a Semiratio-Dependent Predator-Prey System with Two Delays

Abstract

1. Introduction

2. Stability of the Positive Equilibrium and Local Hopf Bifurcations

3. Direction and Stability of the Hopf Bifurcation

4. Numerical Simulation and Discussions

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information