By means of the method of quasi-lower and quasi-upper solutions and monotone iterative technique, we consider the nonlinear boundary value problems with Caputo fractional derivative and introduce two well-defined monotone sequences of quasi-lower and quasi-upper solutions which converge uniformly to the actual solution of the problem, and then the existence results of the solution for the problems are established. A numerical iterative scheme is introduced to obtain an accurate approximate solution and to give one example to demonstrate the accuracy and efficiency of the new approach.

1. Introduction

We are interested in the existence and uniqueness of solution of the following nonlinear boundary value problem of fractional order

()

where 1 < μ ≤ 2, F(t, u) = f₀(t, u) + f₁(t, u) + f₂(t, u), and f_i : [0,1] × R → R(i = 0,1, 2) are a continuous function, α, β ∈ R, and D^μ is the Caputo fractional derivative of order μ.

It is well known that the differential equations with fractional order are generalization of ordinary differential equations to noninteger order, they occur more frequently in different research areas and engineering, such as physics, control of dynamical systems, chemistry and so forth. We also remark that several kinds of fractional derivatives were introduced to investigate the fractional differential equation, see, for example, [1, 2], and references therein.

Roughly speaking, it is a difficult task to give exact solutions for fractional differential equations. Recently, there are a number of numerical and analytical techniques to concerned with such problems, for instance, the homotopy analysis method, the Adomian decomposition method and the critical point theory have been discussed the fractional differential equations, such as [3–9]. On the other hand, very recently, the monotone iterative technique, combined with the method of lower and upper solutions were introduced to study the problems [10–13]. In [10, 11], the authors used the method of lower and upper solutions to investigate the existence of solutions for a class of fractional initial value problems. In [12] the authors considered fractional boundary value problem and proved the existence of solution. In [13], the author discussed the Monotone iterative technique for boundary value problems of a nonlinear fractional differential equation with deviating arguments. Specially, here it is worth mentioning, that Al-Refai and Ali Hajji [14] introduce two well-defined monotone sequences of lower and upper solutions which converge uniformly to the actual solution of the problem. However, the existence results in [14] mainly depend upon a restrictive condition; that is,

()

It is a critical condition in order to discuss the monotone iterative sequences. It is, therefore, natural to ask how to discuss the problem (1), if F(t, u) is not necessary decreasing with respect to u. So, being directly inspired by [14], the purpose of this paper is to study the nonlinear boundary value problems of fractional order with Dirichlet boundary conditions. We introduce a method based on quasi-lower and quasi-upper solutions to prove the existence of a unique solution with no claim on the strictwe monotone. And also give an algorithm to construct two monotone sequences of quasi-lower and quasi-upper solutions. Moreover, the constructed sequences are proved to converge uniformly to the unique solution of the problem.

The paper is organized as follows. Preliminaries are in Section 2. Then in Section 3, we construct the monotone sequences of quasi-lower and quasi-upper solutions and prove their uniform convergence to the unique solution of the problem. Finally, in Section 4, we establish the numerical approach employed to obtain accurate numerical solution, and give one example to demonstrate the accuracy and efficiency of the new approach.

2. Preliminaries

In this sections, we present the definition of a pair of quasi-lower and quasi-upper solutions and some lemmas which will be needed in the next section.

For θ > 0, m − 1 < θ ≤ m, m ∈ N, the Caputo derivative (see [1, 2]) is defined by

()

The Caputo derivative defined in (3) is related to the Riemann-Liuville fractional integral I^θ of θ ∈ R⁺ by

()

where for any δ > 0

()

Moreover,

()

where c_k = h^(k)(0⁺)/k!, 1 ≤ k ≤ m − 1.

Definition 1. The functions v⁽⁰⁾, w⁽⁰⁾ ∈ C²([0,1], R) are called a pair of quasi-lower and quasi-upper solutions of the problem (1), if it satisfies

()

If the above inequalities are equalities, we call v⁽⁰⁾ and w⁽⁰⁾ a pair of quasi-solutions of the problem (1).

Lemma 2 (see [14].)Let p ∈ C²([0,1], R) and C > 0 is a constant. If p(t) satisfies the relations

()

then p(t) ≥ 0 for t ∈ [0,1].

Lemma 3 (see [14].)A function u(t) is a solution of the linear fractional BVP problems

()

if and only if it is a solution of integral equation

()

where

()

Lemma 4. For all t ∈ [0,1], we have

()

where

()

Proof. The proof of this lemma is easy, so we omit it.

In the rest of the paper, for convenience sake, we define the set

()

let

()

and list some conditions.

(C₁) v⁽⁰⁾, w⁽⁰⁾ is a pair of quasi-lower and quasi-upper solutions of the problem (1) and v⁽⁰⁾(t) ≤ w⁽⁰⁾(t), t ∈ [0,1].
(C₂) The function f₁(t, u) is increasing with respect to u, and f₂ is decreasing with respect to u. And there exists a constant M ∈ (0, ΛΓ(μ)) such that
()

Lemma 5. Let (C₁) and (C₂) hold; then for any fixed η₁, η₂ ∈ [v⁽⁰⁾, w⁽⁰⁾], the linear problems

()

have a unique solution

, t ∈ [0,1].

Proof. Firstly, we prove that if is a solution of (17), then . From (C₁), (C₂) and if v⁽⁰⁾ is a quasi-lower solution of the problem (1), then we have

()

Thus from (18) and if

is a solution of (17), set

; then

()

By Lemma 2, we have that

()

That is,

. Similarly, we show

. Therefore,

Next, we show that (17) has a unique solution.

From Lemma 3, the problems (17) are equivalent to the following integral equation

()

where

Let

()

For any

, by Lemma 4 and condition (C₂), we have

()

By the Banach fixed point theorem, the operator 𝒜 has a unique point. This shows that (17) has a unique solution u ∈ [v⁽⁰⁾, w⁽⁰⁾], t ∈ [0,1].

3. Monotone Sequences of Quasi-Lower and Quasi-Upper Solutions

In this sections we construct the monotone sequences of quasi-lower and quasi-upper solutions and prove their uniform convergence to the unique solution of the problem.

Theorem 6. Let (C₁) and (C₂) hold, and assume that (C₃)v^(k), w^(k), k ≥ 1 is a pair of solutions of

()

Then one has the following.

(i)
The sequence v^(k), w^(k) is a pair of quasi-lower and quasi-upper solutions of (1). Moreover,
()
(ii)
The sequence v^(k), w^(k) converges uniformly to v_* and w^*, respectively, with v⁽⁰⁾ ≤ v_* ≤ w^* ≤ w⁽⁰⁾. Moreover, v_* and w^* are a pair of minimal-maximal quasi-solutions of (1) in [v⁽⁰⁾, w⁽⁰⁾].
(iii)
Suppose further that there exist constants L_i > 0(i = 0,1, 2) such that L₁ + L₂ < L₀ ≤ M, and
()
Then v_* = w^* is the actual solution of (1) in [v⁽⁰⁾, w⁽⁰⁾].

Proof. (i) For any fixed η₁, η₂ ∈ [v⁽⁰⁾, w⁽⁰⁾], consider the linear problems

()

By Lemma 5, the linear problems (28) have a unique solution

. Define operator ℬ : [v⁽⁰⁾, w⁽⁰⁾]×[v⁽⁰⁾, w⁽⁰⁾]→[v⁽⁰⁾, w⁽⁰⁾] as follows:

()

Again, it is easy that to prove that η₁, η₂ are a pair of quasi-solutions of the problem (1) if and only if

()

Furthermore, from (28) and condition (C₂), we can prove ℬ[η₁, η₂] is increasing with respect to η₁, and is decreasing with respect to η₂; that is,

()

In fact, setting u₁ = ℬ[η₁, η], u₂ = ℬ[η₂, η], by (28) and condition (C₂), we have

()

Thus, by setting p(t) = u₂(t) − u₁(t), then

()

By Lemma 2, we have that

()

That is, u₂ ≥ v₁, or the first inequality holds in (31). Similarly, the second inequality holds in (31) too.

Again, similar to the previous argument, we can show that

()

Now, let

()

Thus, from (31), (35), and (36), we have

()

Moreover, it is clear that v^(k), w^(k) satisfy (36) if and only if v^(k), w^(k) are a pair of solutions of (25).

To prove (i), we only need to show that v^(k), w^(k) are a pair of quasi-lower and quasi-upper solutions of (1). In fact, from (25) and condition (C₂), we can obtain

()

Hence, v^(k), w^(k) is a pair of quasi-lower and quasi-upper solutions of (1). This proves (i).

(ii) Since the sequence v^(k) is monotone nondecreasing and is bounded from above mention, the sequence w^(k) is monotone nonincreasing and is bounded from below, therefore the pointwise limits exist and these limits are denoted by v_* and w^*. The sequence v^(k), w^(k) are sequences of continuous functions defined on the compact set [0,1], hence By Dini’s theorem [15], the convergence is uniform. This is

()

uniformly on t ∈ [0,1].

Moveover, from (25), we have

()

This show that v_*, w^* are a pair of quasi-solutions of the problem (1).

Now, we prove that v_* and w^* are a pair of minimal-maximal quasi-solutions of (1).

Let v, w ∈ [v⁽⁰⁾, w⁽⁰⁾] be a pair of quasi-solutions of the problem (1), in the following, we show this using induction arguments. In fact, we have

()

Assume that

()

is true. Thus from (31) and (36), we can obtain

()

Therefore,

()

Thus, taking limit in (44) as k → ∞, we have

()

That is, v_* and w^* are a pair of minimal-maximal quasi-solutions of (1) in [v⁽⁰⁾, w⁽⁰⁾].

(iii) Since v_*(t) ≤ w^*(t), t ∈ [0,1], it is sufficient to prove that v_*(t) ≥ w^*(t), t ∈ (0,1). In fact, from (40) and supposition (iii), we have (notice that v_* ≤ w^*)

()

Thus, by setting p(t) = v_* − w^*, from (46), we obtain

()

By Lemma 2 (notice that L₀ − L₁ − L₂ > 0), we have that

()

Therefore, v_* ≥ w^*, t ∈ [0,1]. Hence v_* = w^* is the actual solution of (1) in [v⁽⁰⁾, w⁽⁰⁾]. Thus, we complete this proof.

4. Numerical Implementation

In this section, the numerical procedures are introduced to obtain an approximate solution of (1).

For the problem (25), from Lemma 3, we have

()

Thus by Theorem 6, the unique solution to problem (1) is given by

()

Setting

()

Discretize the interval [0,1] with the nodes h = 1/N, t_i = ih, s_j = jh. Using Simpson’s quadrature rule, we can obtain the function S_Φ(t), and Ψ(t), to approximate the integral

and

on the right hand sid of (49), where

()

where {d_j} are the coefficients in composite Simpson’s quadrature rule: d₀ = d_N = 1, d_2j−1 = 4, d_2j = 2, 1 ≤ j ≤ N/2.

Now, let

, from (49) and the above; we obtain the following linear system of equations mentioned

()

Setting

()

Thus system (54) can be written as a matrix-vector equation

()

where ℐ is the identity matrix.

Remark 7. Applying the above numerical scheme, we can solve iteratively for v^(k) and w^(k) up to some large enough k = K. For a given accuracy ε, we take v^(k) and w^(k) as ε-accurate approximations of v_* and w^*, respectively. And we use

()

to describe the error.

Example 8. Consider the fractional BVP

()

Let

()

It can be easily verified that

()

are a pair of ordered quasi-lower and quasi-upper solutions of (58). Moreover,

()

Thus

()

Hence for this example, we found that, for ε = 10⁻¹⁰, it has K = 10 iterations for E(k) < ε. the graph of v^(k) and w^(k), for some values of k, is in Figure 1. Table 1 displays E(k) versus k for selected values of k.

Table 1. E(k) : k = 2i, i = 0, 1, 2, 3, 4, 5.

k	0	2	4	6	8	10
E(k)	1.000	1.117 × 10⁻²	1.302 × 10⁻⁴	1.259 × 10⁻⁶	1.048 × 10⁻⁸	7.632 × 10⁻¹¹

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Graph of v^(k) and w^(k).

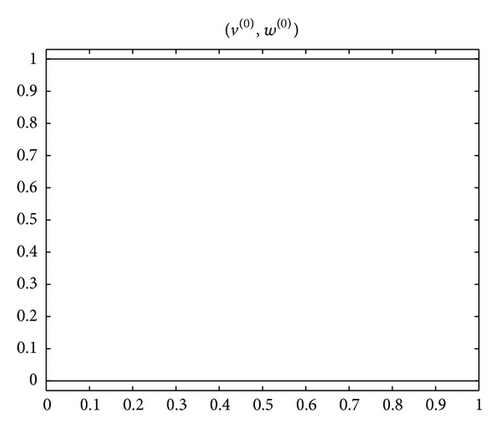
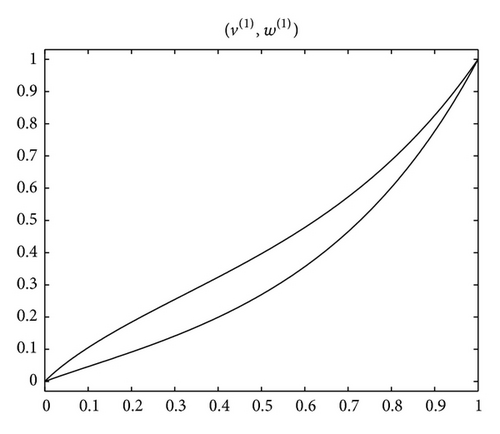
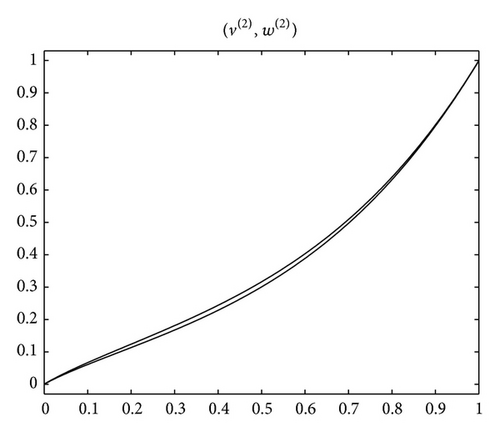
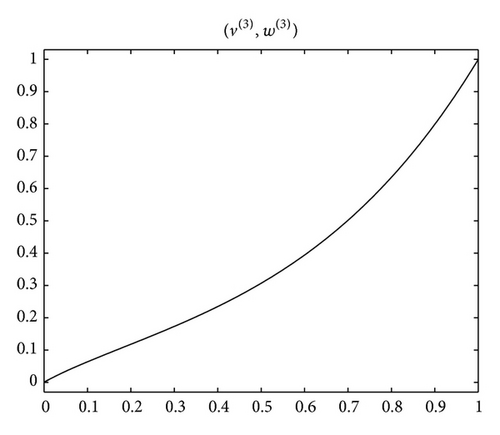
Acknowledgment

This work was partially supported by NNSF of China (Grant no. 11171122).

References

1 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, Mathematics in Science and Engineering, MR1658022, ZBL1056.93542.
Web of Science® Google Scholar
2 Lakshmikantham V., Leela S., and Vasundhara J., Theory of Fractional Dynamic Systems, 2009, Cambridge Academic Publishers, Cambridge, Mass, USA.
Google Scholar
3 Al-Mdallal Q. M., On the numerical solution of fractional Sturm-Liouville problems, International Journal of Computer Mathematics. (2010) 87, no. 12, 2837–2845, https://doi.org/10.1080/00207160802562549, MR2728212, ZBL1202.65100.
10.1080/00207160802562549
Web of Science® Google Scholar
4 Momani S. and Odibat Z., Analytical approach to linear fractional partial differential equations arising in fluid mechanics, Physics Letters A. (2006) 355, 271–279.
10.1016/j.physleta.2006.02.048
CAS Web of Science® Google Scholar
5 Momani S. and Shawagfeh N., Decomposition method for solving fractional Riccati differential equations, Applied Mathematics and Computation. (2006) 182, no. 2, 1083–1092, https://doi.org/10.1016/j.amc.2006.05.008, MR2282552, ZBL1107.65121.
10.1016/j.amc.2006.05.008
Web of Science® Google Scholar
6 Al-Mdallal Q. M., Syam M. I., and Anwar M. N., A collocation-shooting method for solving fractional boundary value problems, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 12, 3814–3822, https://doi.org/10.1016/j.cnsns.2010.01.020, MR2652654, ZBL1222.65078.
10.1016/j.cnsns.2010.01.020
Web of Science® Google Scholar
7 Jiao F. and Zhou Y., Existence results for fractional boundary value problem via critical point theory, International Journal of Bifurcation and Chaos. (2012) 22, no. 4, 1250086, https://doi.org/10.1142/S0218127412500861, MR2926062, ZBL1258.34015.
10.1142/S0218127412500861
Web of Science® Google Scholar
8 Jiao F. and Zhou Y., Existence of solutions for a class of fractional boundary value problems via critical point theory, Computers & Mathematics with Applications. (2011) 62, no. 3, 1181–1199, https://doi.org/10.1016/j.camwa.2011.03.086, MR2824707, ZBL1235.34017.
10.1016/j.camwa.2011.03.086
Web of Science® Google Scholar
9 Li C. F., Luo X. N., and Zhou Y., Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations, Computers & Mathematics with Applications. (2010) 59, no. 3, 1363–1375, https://doi.org/10.1016/j.camwa.2009.06.029, MR2579500, ZBL1189.34014.
10.1016/j.camwa.2009.06.029
Web of Science® Google Scholar
10 Abbas S. and Benchohra M., Upper and lower solutions method for impulsive partial hyperbolic differential equations with fractional order, Nonlinear Analysis: Hybrid Systems. (2010) 4, no. 3, 406–413, https://doi.org/10.1016/j.nahs.2009.10.004, MR2645856, ZBL1202.35340.
10.1016/j.nahs.2009.10.004
Web of Science® Google Scholar
11 Benchohra M. and Hamani S., The method of upper and lower solutions and impulsive fractional differential inclusions, Nonlinear Analysis: Hybrid Systems. (2009) 3, no. 4, 433–440, https://doi.org/10.1016/j.nahs.2009.02.009, MR2561660, ZBL1221.49060.
10.1016/j.nahs.2009.02.009
Web of Science® Google Scholar
12 Shi A. and Zhang S., Upper and lower solutions method and a fractional differential equation boundary value problem, Electronic Journal of Qualitative Theory of Differential Equations. (2009) 30, 1–13, MR2506151, ZBL1183.34009.
10.14232/ejqtde.2009.1.30
Google Scholar
13 Wang G., Monotone iterative technique for boundary value problems of a nonlinear fractional differential equation with deviating arguments, Journal of Computational and Applied Mathematics. (2012) 236, no. 9, 2425–2430, https://doi.org/10.1016/j.cam.2011.12.001, MR2879710, ZBL1238.65077.
10.1016/j.cam.2011.12.001
Web of Science® Google Scholar
14 Al-Refai M. and Ali Hajji M., Monotone iterative sequences for nonlinear boundary value problems of fractional order, Nonlinear Analysis: Theory, Methods & Applications. (2011) 74, no. 11, 3531–3539, https://doi.org/10.1016/j.na.2011.03.006, MR2803080, ZBL1219.34005.
10.1016/j.na.2011.03.006
Web of Science® Google Scholar
15 Royden H. L., Real Analysis, 1988, 3rd edition, Macmillan Publishing Company, New York, NY, USA, MR1013117.
Google Scholar

Citing Literature

All articles

Monotone Iterative Solutions for Nonlinear Boundary Value Problems of Fractional Differential Equation

Abstract

1. Introduction

2. Preliminaries

3. Monotone Sequences of Quasi-Lower and Quasi-Upper Solutions

4. Numerical Implementation

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Monotone Iterative Solutions for Nonlinear Boundary Value Problems of Fractional Differential Equation

Abstract

1. Introduction

2. Preliminaries

3. Monotone Sequences of Quasi-Lower and Quasi-Upper Solutions

4. Numerical Implementation

Acknowledgment

References

Citing Literature

Figures

References

Related

Information