We study how may vary the gravitational and the cosmological “constants,” (G and Λ) in several scalar-tensor theories with Bianchi III, VI₀, and VI_h symmetries. By working under the hypothesis of self-similarity we find exact solutions for two different theoretical models, which are the Jordan-Brans-Dicke (JBD) with Λ(ϕ), and the usual JBD model with potential U(ϕ) (that mimics the behaviour of Λ(ϕ)). We compare both theoretical models, and some physical and geometrical properties of the solutions are also discussed putting special emphasis on the study of the isotropization of the solutions.

1. Introduction

Current observations of the large scale Cosmic Microwave Background (CMB) suggest to us that our physical universe is expanding in an accelerated way. Such observations [1–3] indicate that the universe is dominated by an unidentified “dark energy” (DE) and suggest that this unidentified dark energy has a negative pressure [4–6]. This last characteristic of the dark energy points to the vacuum energy or cosmological constant Λ, as a possible candidate for dark energy. From the theoretical point of view, it is convenient to consider the cosmological constant as a dynamical quantity in order to solve the so-called coincidence and fine tuning problems. In the same way other observations have pointed out a possible variation of the gravitational constant G [7, 8]. For example, observations of Hulse-Taylor binary pulsar [9, 10], and type Ia supernova observations [11]. For an extensive review see Uzan [12].

We have several theoretical models that consider both constants as variable with respect to the cosmic time. Such theories are modified general relativity (MGR), modified scalar cosmological models (MST), and several scalar-tensor theories (STT). The MGR and MST have a drawback, since in them the variations of G and Λ are introduced in an ad hoc manner. Nevertheless we consider that the STT are the best models to study the variation of G and Λ, since they have been deduced form variational principles and where the time dependence can occur in a natural way, without any new assumption or modification of the theory. This class of models has received a renewed interest in recent times, for two main reasons. Firstly, the new inflationary scenario as the extended inflation has a scalar field that solves several problems present in the old theories. Secondly, string theories and other unified theories contain a scalar field which plays a similar role to the scalar field of the STT. The scalar-tensor theories started with the work of Jordan in 1950 [13]. A prototype of such models was proposed by Brans and Dicke in 1961 [14]. Their aim for presenting this model was to modify Einstein’s theory in such a way as to incorporate the so-called “Mach principle.” These theories have been generalized by Bergmann [15], Nordtvedt [16], and Wagoner [17]. For a recent review of this class of theories we refer to [18, 19].

In a recent paper, [20] we have considered a family of scalar-tensor theories under the hypothesis of self-similarity. They are the Jordan-Brans-Dicke model with a dynamical cosmological constant (JBDΛ) [21] and with a potential (JBDU) [19], which is equivalent to a time-dependent cosmological constant. For such theoretical models, we proved how must behave each physical quantity under the hypothesis of self-similarity.

We have focused our attention on this class of solutions, since as has been pointed out by Rosquist and Jantzen [22] (for a precise definition of self similar models, see for instance [23]), self-similar models correspond to equilibrium points, playing a dominant role in the dynamics of Bianchi cosmological models. For this reason, Coley [24] has stressed the fact that self-similar models play an important role in describing the asymptotic dynamics of the Bianchi models. A large class of orthogonal spatially homogeneous models (including all class B models) are asymptotically self-similar at the initial singularity and are approximated by exact perfect fluid or vacuum self-similar power-law models. In the same way, exact self-similar power-law models can also approximate general Bianchi models at intermediate stages of their evolution and which is also important, and self-similar solutions can describe the behavior of Bianchi models at late times. Furthermore working under the hypothesis of self-similarity allows us to find exact power-law solutions in such a way that we may compare the obtained solution for each studied model.

By applying the theoretical results obtained in [20] we have studied how may vary G and Λ in the described theoretical models using different geometries as Bianchi I [25], Bianchi II [26], Bianchi V, VII_h and IX [27] and Kantowsky-Sach [20]. In this paper, enlarging the program, we would like to study the case of family of Bianchi VI geometry, that is, Bianchi III, VI ₀, and VI _h.

Therefore, the paper is organized as follows. In Section 2 we start by revising the theoretical results obtained in [20]. Once all the theoretical ingredients have been exposed, in Section 3 we begin describing the main results concerning to the Bianchi VI geometry and its self-similar restrictions. Section 4 is devoted to find exact self-similar solutions for the described theoretical models: JBDΛ and JBDU. We put special emphasis on the study of the isotropization of the solutions. We end in Section 5 with a brief summary of the main results and conclusions.

2. Theoretical Models

The first of the scalar-tensor model is described by the field equations [21]:

, where G_ij is the Einstein tensor

(1)

and

is the effective stress-energy tensor defined by

(2)

where

is the stress-energy tensor of the ordinary matter, in this case a perfect fluid model defined by

(3)

and where the 4-velocity is defined by u_i = (1,0, 0,0), ρ_m is the energy density, and p_m is the pressure. They are related by the equation of state (EoS): p_m = γρ_m, with γ ∈ (−1,1].

is defined as follows:

(4)

where ϕ is the scalar function, considering only that ϕ = ϕ(t) and Λ(ϕ) is a potential function and plays the role of a cosmological constant, and ω(ϕ) is the coupling function of the particular theory (the Brans-Dicke parameter), that could be considered as variable.

The conservation equations are

(5)

where

is the trace of the stress-energy tensor and C = 3 + 2ω(ϕ). The gravitational coupling G_eff(t) is given by

(6)

In a recent paper [20], we have proved that in the framework of self-similar and power-law solutions the main quantities must behave as follow:

(7)

in such a way that the parameters must verify the following relationship:

, with α = (1 + γ)h, h being a positive constant, that it is defined by the exponents (a_i) of the scale factor of the metric (we are only interested in power-law and self-similar solutions), and h = ∑_i a_i.

The second theoretical model is described by the following field equations (see, for instance, [18, 20]):

(8)

with

(9)

and the conservation equations for the scalar and matter fields

(10)

where R is the scalar curvature and F_ϕ = dF/dϕ. The function U(ϕ) plays the role of a dynamical cosmological constant. The effective gravitational constant G_eff between two test masses measured in laboratory Cavendish-type experiments is given by

(11)

If F(ϕ) = ϕ, Z = ω(ϕ)/ϕ, then we obtain

(12)

with

(13)

where

is defined by (3),

is defined by (4), and the reduced equation of motion for ϕ yields

(14)

with C = 3 + 2ω. Ordinary matter satisfies the conservation equation

. Therefore, in this model, the effective gravitational constant G_eff behaves as

(15)

As we have shown in [20], in the framework of self-similar and power-law solutions, the main quantities must behave as follows:

(16)

where

, such that

. Note that as in the Λ model, α = h(γ + 1).

3. The Metric

Throughout the paper M will denote the usual smooth (connected, Hausdorff, fourdimensional) spacetime manifold with smooth Lorentz metric g of signature (−, +, +, +) (see, for instance, [28]). Thus M is paracompact. A comma, semicolon and the symbol ℒ denote the usual partial, covariant, and Lie derivative, respectively, the covariant derivative being with respect to the Levi-Civita connection on M derived from g. The associated Ricci and stress-energy tensors will be denoted in component form by R_ij () and T_ij, respectively. We will use a system of units where c = 1.

A Bianchi VI spacetime is a spatially homogeneous spacetime which admits a group of isometries G₃, acting on spacelike hypersurfaces, generated by the spacelike Killing vectors field (KVs):

(17)

and therefore the nonzero structure constants are

. In synchronous coordinates, the metric is

(18)

where the metric functions a(t), b(t), and d(t) are functions of the time coordinate t only. As it is observed, the metric (18) collapses to the following cases:

(1) if m = −n, then the metric collapses to Bianchi type V
(19)
with
(20)
and therefore ;
(2) if n = 0, then the metric collapses to Bianchi type III
(21)
with the following KVF:
(22)
and therefore ;
(3)
if m = n = 0, then the model collapses to Bianchi I model
(23)
with
(24)
and .

For the metric (18) we may find the following homothetic vector field (HVF) ℋ, defined by ℒ_ℋg_ij = 2αg_ij (see [22, 23]):

(25)

with the following restrictions on the scale factors:

(26)

where a₁, a₂ ∈ ℝ, and without loss of generality we may set d₀ = 1. In this way the HVF may be written in the following form:

(27)

in such a way that the metric (18) collapses to

(28)

The Hubble parameter H, under these restrictions, is defined by

(29)

with h = a₁ + a₂ + 1.

In this paper we study the following cases.

(1) Model Bianchi type III (BIII), where its metric is defined by
(30)
or
(31)
that is, m = 0 and a₂ = a₃ = 1 or n = 0 and a₁ = a₃ = 1. With these restrictions the deceleration q, anisotropic (𝒜, 𝒲²), and gravitational entropy P² parameters yield
(32)
where σ² = σ_ijσ^ij is the square shear and I₃ = C^abcdC_abcd is the Weyl curvature scalar (see for instance [29]). The second Kretschmann scalar I₂ is defined by I₂ = R_ijR^ij; for a precise definition of gravitational entropy, see [30].
(2) Model Bianchi type VI ₀ (BVI₀), described by the metric
(33)
with m = n, a₁ = a₂, and a₃ = 1. The main kinematical quantities yield
(34)
We also may define a BVI₀ metric by following the way suggested by Stephani et al. [28], that is, by considering the KVF:
(35)
with
(36)
and therefore we obtain
(37)
but as we have pointed out in [31], with this metric we obtain a very complicate field equation (FE), since they depend on trigonometric functions.
(3) To end, a Bianchi type VI_h (BVI_h) is defined by
(38)
with m ≠ n, a₁ ≠ a₂, and a₃ = 1. With these restrictions, we obtain
(39)
where
(40)
For the metric (18) the Einstein tensor yields
(41)
where A = mn − m² − n².

4. Solutions

4.1. Model with Cosmological Constant (JBDΛ)

For the metric (18), the effective stress-energy tensor (2) yields

(42)

Once we have defined the field equations, we next find exact self-similar solutions for the different exposed models.

4.1.1. Bianchi III Solution

For this metric, we have found the following solution:

(43)

where

(44)

In the first place, we would like to stress that the cosmological constant vanishes, so this model does not describe its possible variation. By fixing the Brans-Dicke parameter, ω = 4 · 10⁴ [32], we may see that the solution is valid for all γ ∈ (−1/3, 0), since the energy density ρ behaves as a positive decreasing time function for these values of the EoS (we have set ϕ₀ > 0 for physical reasons). The solution is not inflationary for all γ ∈ (−1/3, 0), precisely q < 0 only if γ < −1/3. With regard to the anisotropic parameters, we find that the solution cannot be considered as isotropic with regard to the first anisotropic parameter, since , for all γ ∈ (−1/3, 0), that is, ; note that when γ tends to zero, 𝒜 takes the value 5/2. Nevertheless, we may say that the solution is isotropic with regard to the second anisotropic parameter, since 𝒲² ≪ 0.0004, for all γ ∈ (−1/3, 0). The gravitational entropy P² ∈ [0,0.2); it does not show any pathological behaviour and takes values close to zero for all γ ∈ (−1/3, 0). To end the analysis of this solution, the effective gravitational constant behaves as a time decreasing function for all γ ∈ (−1/3, 0), since for these values the parameter is positive.

4.1.2. Bianchi VI₀ Solution

By solving the associated algebraic system to the FE we have found the following solution:

(45)

with

(46)

As we may observe, we have again obtained Λ₀ = 0, which is not in agreement with the current observations and which is worse, and we cannot describe its possible time variation. The solution is only valid for all γ ∈ (−1/3, 1) = I, since for these values of the EoS, the energy density is positive, that is, ρ₀ > 0. By setting the Brans-Dicke parameter, ω = 4 · 10⁴, we find that the parameter vanishes at γ_c = 1/3, being positive, , for all γ ∈ (−1/3, 1/3); therefore, the effective gravitational constant G_eff is decreasing when γ < 1/3, for all γ ∈ I, constant at γ_c = 1/3, and growing when for all γ ∈ (1/3, 1). The solution is not inflationary, since the deceleration parameter is always positive, q > 0 for all γ ∈ I. Nevertheless we may conclude that the solution is isotropic, since both anisotropic parameters are close to zero, 𝒜 ∈ (0,1), in such a way that 𝒜 → 1 only when γ → 1, while 𝒲² ≪ 0.01, for all γ ∈ I. However, the gravitational entropy only takes values close to zero in a small neighborhood of γ = −1/3, tending to −∞ in the rest of the interval.

4.1.3. Bianchi VI_h Solution

In this case we have obtained the following solution:

(47)

being only valid for γ = 1/3; note that for this value the wave equation for the scalar field is easier to solve than in the previously cases, since the trace of the matter stress-energy tensor vanishes. In this solution the cosmological constant takes values different than zero, that is, Λ₀ ≠ 0, so we are able to describe its behaviour. We have expressed the solution depending on two parameters, a₁ and a₂; therefore it is necessary to carry out a numerical analysis in order to interpreted it. As usual, we start by fixing the numerical value of the Brans-Dicke parameter, ω = 4 · 10⁴, and we consider that the parameters of the scale factors a₁ and a₂ vary in the interval (0,1). In the first place we have calculated the set of values where the parameters

vanish. In Figure 1 we have plotted this situation finding that the solution is only valid within this small tubular neighborhood. In Figure 2, we have detailed how behave each parameter Λ₀, ρ₀, and

. As we can see, the energy density is positive in this small tubular neighborhood where furthermore the cosmological constant is also positive expect in a very small subinterval where it is negative and vanishes (see Figure 2).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Solution to Bianchi VI _h with CC. Plot of the parameters Λ₀ = 0 (blue) and ρ₀ = 0 (red).

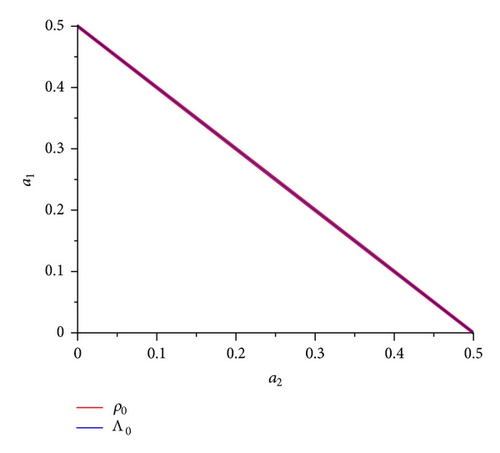
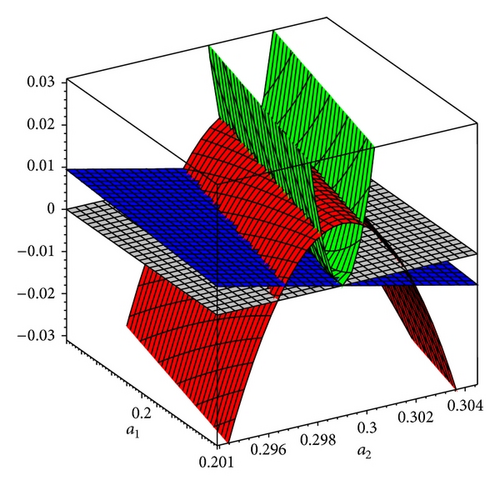
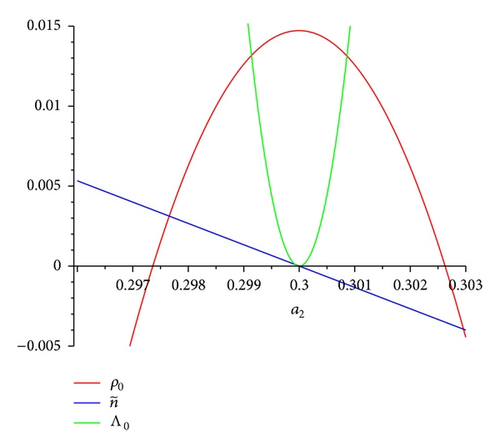
If, for example, we set a₁ = 1/5, then we have obtained the following results (see Figure 3). The energy density parameter ρ₀ is only positive, ρ₀ > 0, if and only if a₂ ∈ (0.2973605134,0.3026282371) = I₁, while the cosmological constant is negative, Λ₀ < 0, if and only if a₂ ∈ (0.2999893937,0.3000106065) = I₂, note that I₂ ⊂ I₁, finding that, Λ₀ ≥ 0, for all a₂ ∈ I₁∖I₂. In the same way, we may see that the parameter of the scalar field, , only vanishes, , if a₂ = 0.3000106065. In this way we may arrive at the conclusion that the effective gravitational constant G_eff is decreasing if a₂ ∈ (0.2973605134,0.3000106065), constant at a₂ = 0.3000106065, where furthermore Λ₀ = 0 and G = G₀, and if a₂ ∈ (0.3000106065,0.3026282371), then G_eff is growing and Λ₀ > 0.

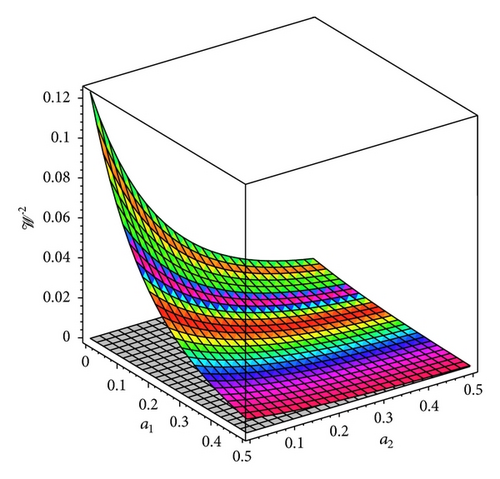
The solution is not inflationary, since the deceleration parameter q is positive in I₁, and we may say that it is isotropic, since both anisotropic parameters take values close to zero (see Figure 4); only when a₁ and a₂ tend to zero (which is not physically realistic) we may observe that 𝒜 ≈ 0.6, while 𝒲² ≈ 0.12. The gravitational entropy takes the following values: P² ≈ −5 in I₁.

4.2. Model with Potential (JBDU)

In this section we consider the theoretical model of the Jordan-Brans-Dicke with potential. For the metric (18), the effective stress-energy tensor (13) yields

(48)

With these FE and the conservations ones we have obtained the following solution for each of the studied cases.

4.2.1. Bianchi III Solutions

For this model we have get two solutions.

(1) For the first solutions we have obtained the following results:
(49)
From the expression for γ we may obtain an exact expression for a₂, getting
(50)
and therefore we obtain the following results for the parameters and q:
(51)
Therefore, we begin by studying the set of points where the scale factor a₂ vanishes, so
(52)
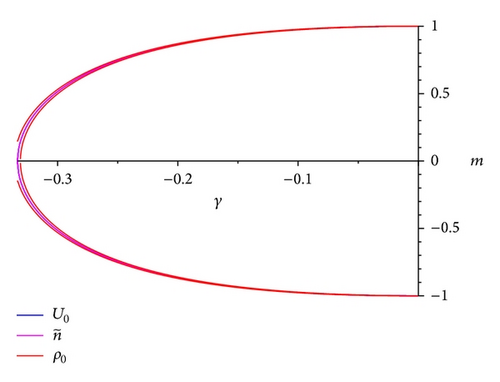
and, in the same way, we calculate the set of values where the parameters vanish. The numerical analysis performed shows us that the energy density is only positive in a small tubular neighborhood with γ ∈ (−1/3,0) and m ∈ (−1,1). In the same neighborhood the potential U and the parameter vanish (see Figure 5).
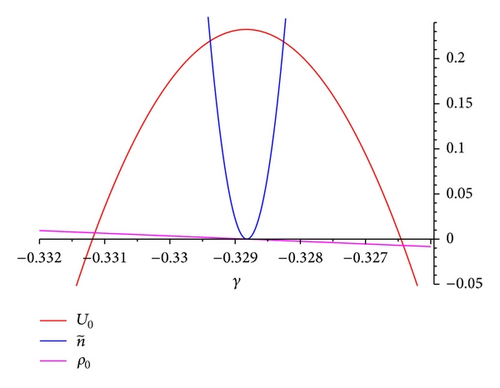
If, for example, we set m = 1/5 and the Brans-Dicke parameter, ω = 4 · 10⁴, we may see in Figure 6 that the solution is only valid for all γ ∈ (−0.3311865733, −0.3264562742) = ℰ(γ_c), that is, a neighborhood of a critical value of the EoS γ_c = −0.328, since the energy density only is positive in this neighborhood, ρ₀ > 0, where furthermore the scalar field is also positive, ϕ₀ > 0 (see Figure 6). In this interval the potential function (the cosmological constant) behaves as follow: U₀ = 0 if and only if γ₁ = −0.3288254637, and γ₂ = −0.3288130902, in such a way that U₀ ≤ 0, for all γ ∈ (γ₁, γ₂), being positive in the rest of the interval. The parameter of the scalar field vanishes at γ₂, being if γ < γ₂ and if γ > γ₂; therefore, the effective gravitational constant decreases if γ < γ₂ is constant at γ = γ₂ and is growing when γ > γ₂, for all γ ∈ ℰ(γ_c).
The solution is not inflationary, since q > 0 for all γ ∈ (−1/3,0) and m ∈ (−1,1). To end, we may say that the solution isotropizes since 𝒜 → 0 and 𝒲² ≪ 0.0001. In the same way we conclude that the gravitational entropy takes values very close to zero in the interval ℰ(γ_c).
(2) In the second solution we get U₀ = 0. This solution is equal to the obtained one in the case of JBDΛ, so the conclusions are the same as the obtained ones in such case.

4.2.2. Bianchi VI₀ Solutions

We have obtained two solutions for this case.

(1) In the first of them we get a₁ = a₂, a₃ = 1, m = n, and U₀ ≠ 0, obtaining
(53)
From the expression of γ, we get a₂:
(54)
where
(55)
and therefore
(56)
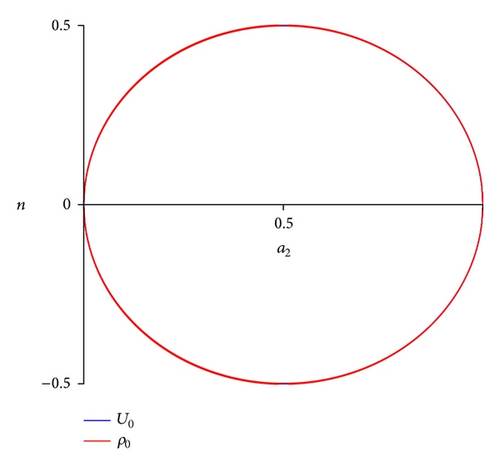
As mentioned above, we need to perform a numerical analysis to analyze the solution. With ω = 4 · 10⁴, we find that the quantities only vanish in a tubular neighborhood, being the solution valid if a₂ ∈ (0,1) and n ∈ (−1/2,1/2) as it is shown in Figure 7.
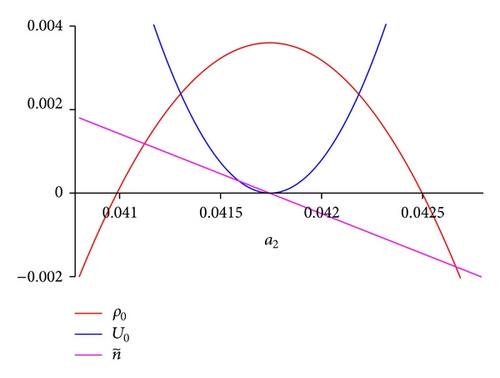
If, for example, we set n = 1/3, then we may understand how each quantity behaves. The energy density is only positive, ρ₀ > 0, in the interval for all γ ∈ (0.12584,0.12879) = ℰ(γ_c) = I, that is, in a small neighborhood of the critical value of the EoS γ_c = 0.1273. As we can see in Figure 8 in such interval the scalar field is also positive ϕ₀ > 0. The potential U behaves as follows: U₀ = 0 if and only if γ₁ = 0.127322 and γ₂ = 0.127325, so U₀ ≤ 0, for all γ ∈ (γ₁, γ₂) = I₂, and therefore U > 0, for all γ ∈ I∖I₂.
The parameter vanishes at γ₁ in such a way that if γ < γ₁ and if γ > γ₁; therefore, the effective gravitational constant G_eff behaves as a growing time function if γ < γ₁, and it is constant at γ = γ₁ and is decreasing if γ > γ₁, for all γ ∈ ℰ(γ_c). The solution is not inflationary, q > 0 for all a₂ ∈ (0,1) and n ∈ (−1/2,1/2). With regard to the isotropization of the solution, we reach the conclusion that it isotropizes, since 𝒜 → 0, and 𝒲² ≪ 0.035 for all a₂ ∈ (0,1) and n ∈ (−1/2,1/2). In the same way, the gravitational entropy takes values very close to zero.
(2) With regard to the second solution, we have obtained U₀ = 0, and therefore it is similar to the obtained one in the model JBDΛ.

4.2.3. Bianchi VI_h Solution

We have only obtained one solution which quite similar to the obtained one in the model JBDΛ. The solution is the following one:

(57)

Therefore we arrive at the same conclusions as in the previously model with Λ(ϕ).

5. Conclusions

We have studied how may vary the “constants” G and Λ (or U) in two different scalar-tensor models: the JBD model with Λ and the JBD model with potential U. Under the hypothesis of self-similarity we have been able to obtain exact solutions for the Bianchi VI geometry (including types III, VI ₀, and VI _h), which allow us to compare them. We have reached the conclusion that the possible variation of the cosmological constant is better described within the JBDU theoretical framework, since with the JBDΛ model Λ usually vanishes. We have summarized in Table 1 the set of solutions that we have found for both models, JBDΛ and JBDU.

Table 1. Summary of the solutions.

Model	Λ		U
III	Λ = 0, G↘, γ ∈ (−1/3,0)	⇔	U = 0, (case Λ)
III			U > 0, G ~ G(γ_c, m) γ ∈ (−1/3,0) 𝒜
VI₀	Λ = 0, G ~ G(γ), γ ∈ (−1/3,1) 𝒜	⇔	U = 0, (case Λ)
VI₀			U > 0, G ~ G(a₂, n) γ ∈ (−1/3,1) 𝒜
VI_h	Λ > 0, G ~ G(a₁, a₂), γ = 1/3 𝒜	⇔	U > 0, G ~ G(a₁, a₂), γ = 1/3 𝒜

With regard to the first of the studied models, the JBDΛ, we have been able to obtain a solution for each geometry. The first of them (Bianchi III) is only valid for all γ ∈ (−1/3,0) and predicts that the cosmological constant vanishes, Λ = 0, which is in contradiction with the current observations. Nevertheless we have studied this solution reaching the conclusion that it is noninflationary and does not isotropize with respect to the first anisotropic parameter 𝒜. The effective gravitational constant G_eff is always decreasing for all γ ∈ (−1/3,0). In the case of the Bianchi type VI ₀ we have found that the cosmological constant is also zero, Λ = 0, but the solution is valid for all γ ∈ (−1/3,1). The effective gravitational constant G_eff shows a different behaviour depending on the EoS γ. It may be growing if γ > 1/3, constant at γ = 1/3, and it behaves as a decreasing time function if γ < 1/3, where γ ∈ (−1/3,1). The solution isotropizes, and it is noninflationary. The solution obtained for the model Bianchi type VI _h has a nonzero cosmological constant, Λ ≠ 0, but the solution is only valid for a particular value of the EoS, γ = 1/3. It is also noninflationary, and it isotropizes. The numerical analysis carryout shows us that the solution is only valid in a small tubular neighborhood, where a₁, a₂ ∈ (0,1/2) in fact the amplitude of this neighborhood depends on the value of the Brans-Dicke parameter ω in such a way that if future observations fix an upper limit for this constant then the diameter of this tubular neighborhood will be small. In this tubular neighborhood, the energy density is positive as well as the cosmological constant Λ. However, there is a really small subtubular neighborhood where Λ vanishes, or it is negative. In this way we have concluded that the solution predicts a Λ > 0 (except within this subtubular neighborhood) in agreement with the observations, while the effective gravitational constant may be growing, constant at a critical point γ_c (where the parameter vanishes), and decreasing.

With regard to the model with potential, JBDU, we have obtained solutions similar to the obtained ones in the model JBDΛ, and therefore we have reached the same conclusions. Nevertheless we have also obtained other solutions which predict a nonvanishing cosmological constant, in this case U ≠ 0, for the geometries Bianchi types III and VI ₀. In the case of the Bianchi type III, the solution is only valid in a small tubular neighborhood, where γ ∈ (−1/3,0) and m ∈ (−1,1). In this tubular neighborhood the energy density is positive, and the solution predicts that the potential function U (that mimics the behaviour of the cosmological constant) is also positive except in a very small subtubular neighborhood where it is negative or vanishes. Within this neighborhood the effective gravitational constant may be growing, constant at a critical point γ_c (where the parameter vanishes), or decreasing depending of the values of γ and n. To end, the solution found for the model Bianchi type VI ₀ with U ≠ 0 is only valid in a small tubular neighborhood, where a₂ ∈ (0,1) and n ∈ (−1/2,1/2), it is noninflationary and isotropizes. In this neighborhood the quantities ρ, U, and G_eff show similar behaviour as the described ones in this kind of solutions, that is, ρ > 0, U > 0 (except in a small subtubular neighborhood), and G_eff is growing, constant, or decreasing depending on the parameters a₂ and n.

References

1 de Bernardis P., Ade P. A. R., Bock J. J. et al., A flat Universe from high-resolution maps of the cosmic microwave background radiation, Nature. (2000) 404, 955–959, https://doi.org/10.1038/35010035.
Google Scholar
2 Hanany S., Ade P., Balbi A. et al., MAXIMA-1: a measurement of the cosmic microwave background anisotropy on angular scales of 10′-5°, The Astrophysical Journal Letters. (2000) 545, no. 1, L5–L9, https://doi.org/10.1086/317322.
Google Scholar
3 Balbi A., Ade P., Bock J. et al., Constraints on cosmological parameters from MAXIMA-1, The Astrophysical Journal Letters. (2000) 545, no. 1, L1–L4, https://doi.org/10.1086/317323.
Google Scholar
4 Perlmutter S., Aldering G., Della Valle M. et al., Discovery of a supernova explosion at half the age of the Universe, Nature. (1998) 391, no. 6662, 51–54, https://doi.org/10.1038/34124.
Google Scholar
5 Perlmutter S., Aldering G., Goldhaber G. et al., Measurements of Ω and Λ from 42 high-redshift supernovae, Astrophysical Journal. (1999) 517, no. 2, 565–586, https://doi.org/10.1086/307221.
Google Scholar
6 Garnavich P. M., Kirshner R. P., Challis P. et al., Constraints on cosmological models from Hubble space telescope observations of high-z supernovae, The Astrophysical Journal Letters. (1998) 493, no. 2, L53–L57, https://doi.org/10.1086/311140.
Google Scholar
7 Innocenti S. D., Fiorentini G., Raffelt G. G., Ricci B., and Weiss A., Time variation of Newton′s constant and the age of globular clusters, Astronomy & Astrophysics. (1996) 312, 345–352.
Google Scholar
8 Umezu K., Ichiki K., Yahiro M. et al., Cosmological constraints on Newton’s constant, Physical Review D. (2005) 72, no. 4, 5, 044010, https://doi.org/10.1103/PhysRevD.72.044010.
Google Scholar
9 Bisnovatyi-Kogan G. S., Checking the variability of the gravitational constant with binary pulsars, International Journal of Modern Physics D. (2006) 15, no. 7, 1047–1052, https://doi.org/10.1142/S0218271806008747.
Google Scholar
10 Damour T., Gibbons G. W., and Taylor J. H., Limits on the variability of G using binary-pulsar data, Physical Review Letters. (1988) 61, no. 10, 1151–1154, https://doi.org/10.1103/PhysRevLett.61.1151.
Google Scholar
11 Riess A., Filippenko A. V., Challis P. et al., Observational evidence from supernovae for an accelerating universe and a cosmological constant, The Astronomical Journal. (1998) 116, no. 3, 1009–1038, https://doi.org/10.1086/300499.
Google Scholar
12 Uzan J. P., Varying constants, gravitation and cosmology, Living Reviews in Relativity. (2011) 14, no. article 2, https://doi.org/10.12942/lrr-2011-2.
Google Scholar
13 Jordan P., Schwerkraft und Weltall, 1955, Vieweg Braunschweig.
Google Scholar
14 Brans C. and Dicke R. H., Mach′s principle and a relativistic theory of gravitation, Physical Review. (1961) 124, no. 3, 925–935, 2-s2.0-36149020547, https://doi.org/10.1103/PhysRev.124.925.
Google Scholar
15 Bergmann P. G., Comments on the scalar-tensor theory, International Journal of Theoretical Physics. (1968) 1, no. 1, 25–36, https://doi.org/10.1007/BF00668828.
Google Scholar
16 NordtvedtK.Jr., Post-Newtonian metric for a general class of scalar-tensor gravitational theories and observational consequences, Astrophysical Journal. (1970) 161, 1059–1067.
Google Scholar
17 Wagoner R. V., Scalar-tensor theory and gravitational waves, Physical Review D. (1970) 1, no. 12, 3209–3216 , https://doi.org/10.1103/PhysRevD.1.3209.
Google Scholar
18 Fujii Y. and Maeda K., The Scalar-Tensor Theory of Gravitation, 2003, Cambridge University Press.
Google Scholar
19 Faraoni V., Cosmology in Scalar-Tensor Gravity, 2004, Kluwer Academic, Dordrecht, The Netherlands.
Google Scholar
20 Belinchón J. A., Generalized self-similar scalar-tensor theories, The European Physical Journal C. (2012) 72, https://doi.org/10.1140/epjc/s10052-012-1866-8.
Google Scholar
21 Will C. M., Theory and Experiments in Gravitational Physics, 1993, revised edition, Cambridge University Press.
10.1017/CBO9780511564246
Google Scholar
22 Rosquist K. and Jantzen R. T., Spacetimes with a transitive similarity group, Classical and Quantum Gravity. (1985) 2, no. 6, article 004, L129–L133, 2-s2.0-0000637387, https://doi.org/10.1088/0264-9381/2/6/004.
Google Scholar
23 Carr B. J. and Coley A. A., Self-similarity in general relativity, Classical and Quantum Gravity. (1999) 16, no. 7, article R31, https://doi.org/10.1088/0264-9381/16/7/201.
Google Scholar
24 Coley A. A., Dynamical Systems and Cosmology, 2003, Kluwer Academic, Dordrecht, The Netherlands.
Google Scholar
25 Belinchón J. A., Bianchi I in scalar and scalar-tensor cosmologies, Central European Journal of Physics. (2012) 10, no. 4, 789–798, https://doi.org/10.2478/s11534-012-0087-y.
Google Scholar
26 Belinchón J. A., Exact self-similar Bianchi II solutions for some scalar-tensor theories, Astrophysics and Space Science. (2013) 345, no. 2, 387–397, https://doi.org/10.1007/s10509-013-1396-3.
Google Scholar
27 Belinchón J. A., (An)Isotropic models in scalar and scalar-tensor cosmologies, Astrophysics and Space Science. (2012) 338, no. 2, 381–400, https://doi.org/10.1007/s10509-011-0954-9.
Google Scholar
28 Stephani H., Kramer D., MacCallum M., Hoenselaers C., and Herlt E., Exact Solutions of Einstein′s Field Equations, 2003, Cambridge University Press.
Google Scholar
29 Nilsson U. S., Uggla C., Wainwright J., and Lim W. C., An almost isotropic cosmic microwave temperature does not imply an almost isotropic universe, The Astrophysical Journal Letters. (1999) 522, no. 1, https://doi.org/10.1086/312209.
Google Scholar
30 Wainwright J. and Anderson P. J., Isotropic singularities and isotropization in a class of Bianchi type-VI_h cosmologies, General Relativity and Gravitation. (1984) 16, no. 7, 609–624, https://doi.org/10.1007/BF00767856.
Google Scholar
31 Belinchón J. A., Self-similar scalar cosmologies, Gravitation and Cosmology. In press.
Google Scholar
32 Bertotti B., Iess L., and Tortora P., A test of general relativity using radio links with the Cassini spacecraft, Nature. (2003) 425, no. 6956, 374–376, 2-s2.0-0141620355, https://doi.org/10.1038/nature01997.
Google Scholar

All articles

Scalar-Tensor Bianchi VI Models

Abstract

1. Introduction

2. Theoretical Models

3. The Metric

4. Solutions