Abstract and Applied Analysis
Volume 2013, Issue 1 461970
Research Article
Open Access

The Bernstein Operational Matrices for Solving the Fractional Quadratic Riccati Differential Equations with the Riemann-Liouville Derivative

Dumitru Baleanu, 

Dumitru Baleanu

Department of Mathematics, Cankaya University, Ogretmenler Cad. 14, Balgat, 06530 Ankara, Turkey cankaya.edu.tr

Institute of Space Sciences, P.O. Box MG 23, Magurele, 077125 Bucharest, Romania spacescience.ro

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, P.O. Box 80204, Jeddah 21589, Saudi Arabia kau.edu.sa

Search for more papers by this author
Mohsen Alipour, 

Corresponding Author

Mohsen Alipour

Faculty of Basic Science, Babol University of Technology, P.O. Box 47148-71167, Babol, Iran ikiu.ac.ir

Search for more papers by this author
Hossein Jafari, 

Hossein Jafari

Department of Mathematics, University of Mazandaran, P.O. Box 47416-95447, Babolsar, Iran umz.ac.ir

Search for more papers by this author
First published: 20 June 2013
https://doi.org/10.1155/2013/461970
Citations: 11
Academic Editor: Ali H. Bhrawy

Abstract

We obtain the approximate analytical solution for the fractional quadratic Riccati differential equation with the Riemann-Liouville derivative by using the Bernstein polynomials (BPs) operational matrices. In this method, we use the operational matrix for fractional integration in the Riemann-Liouville sense. Then by using this matrix and operational matrix of product, we reduce the problem to a system of algebraic equations that can be solved easily. The efficiency and accuracy of the proposed method are illustrated by several examples.

1. Introduction

The Riccati differential equation is named after the Italian Nobleman Count Jacopo Francesco Riccati (1676–1754). The book of Reid [1] contains the fundamental theories of the Riccati equation, with applications to random processes, optimal control, and diffusion problems. Moreover, it is well known that the one-dimensional static Schrödinger equation is closely related to a Riccati differential equation [2]. Solitary wave solution of a nonlinear partial differential equation can be represented as a polynomial in two elementary functions satisfying a projective Riccati equation [3].

In this paper, we are dealing with the fractional quadratic Riccati differential equation as follows:
()
subject to the initial conditions
()
where   (k = 0, 1, …, ⌈α⌉ − 1) are constants and a(t), b(t), and f(t) are known functions. We can see [4] to guarantee the existence and uniqueness of the solution of (1) with initial conditions (2).

The general response expression (1) contains a parameter α, the order of the fractional derivative that can be varied to obtain various responses. In the case that α is integer, then (1) is reduced to the classical Riccati differential equation.

This problem to develop the analytical and numerical method to solve the Riccati differential equation with standard derivative, the Caputo fractional derivative and the Riemann-Liouville fractional derivative, has attracted much attention and has been studied by many authors [5–18].

The aim of this work is using the Bernstein polynomials for solving the problem (1) and (2). We notice that the problem presented [18] was in the Caputo sense but in our work, the problem is with the Riemann-Liouville derivative; therefore we considered a more general space of functions. Also, in [18], the authors used the polynomials in the form of =   (i = 0, 1, …, m) that is different from the standard Bernstein polynomials. So, the operational matrices in this work are different from those in [18].

The organization of this paper is as follows. In Section 2, the Bernstein polynomials are introduced. Some basic definitions and properties of the fractional calculus and also the BPs operational matrix for the Riemann-Liouville fractional integration are presented in Section 3. In Section 4, by BPs operational matrices, we solve the fractional quadratic Riccati differential equation. In Section 5, we discuss the convergence of the proposed method. In Section 6, several examples are considered to evaluate the power and effectiveness of the presented method. Some conclusions are summarized in the last section.

2. The Bernstein Polynomials and Their Properties

On the interval [0, 1] we define the Bernstein polynomials (BPs) of mth degree as follows [19]:
()
Set {B0,m(x), B1,m(x), …, Bm,m(x)} in the Hilbert space L2[0, 1] is a complete basis. We can write Φm(x) = ATm(x), where A is a matrix upper triangular, , and [20].
As a result, any polynomial of degree m can be expanded in terms of linear combination of Bi,m(x)  (i = 0, 1, …, m) as given below:
()
where
()
The approximation of functions within the Bernstein polynomials and convergence analysis can be found in [20, 21].

3. BPs Operational Matrix for the Riemann-Liouville Fractional Integration

In this section, firstly, we give some basic definitions and properties of the fractional calculus which are used further in this paper.

Definition 1 (see [4], [22]–[24].)Let α ≥ 0; the operator , defined on L1[a, b] by

()
is called the Riemann-Liouville fractional integral operator of order α.

Definition 2 (see [4], [22]–[24].)Let α ≥ 0 and n = ⌈α⌉; the operator , defined by

()
is called the Riemann-Liouville fractional derivative operator of order α.

Definition 3 (see [4], [22]–[24].)Let α ≥ 0, n = ⌈α⌉, and dnf(x)/dxn∈L1[a, b]. The operator , defined by

()
is called the Caputo fractional derivative operator of order α.

Lemma 4. If α ≥ 0, n = ⌈α⌉, and a ≤ t ≤ b, then

()
()
()

Proof. See [22–24].

Theorem 5. One can get BPs operational matrix Fα   from order (m + 1)×(m + 1) for the Riemann-Liouville fractional integral as

()

Proof. See [21].

4. BPs for Solving the Fractional Quadratic Riccati Differential Equation

Firstly, we use the initial conditions to reduce a given initial-value problem to a problem with zero initial conditions.

So, we define
()
where is some known function that satisfied the initial conditions (2) and z(t) is a new unknown function.
Substituting (13) in (1) and (2), we have an initial-value problem as follows:
()
subject to the initial conditions
()
On the other hand, by (11) in Lemma 4 we can write
()
Also, by using Lemma 3.3 in [20] the inputs , , , and can be approximated as follows:
()
()
()
()
where F, A, and B are known (m + 1) column vectors and C is an unknown (m + 1) column vector.
From (10), (15), (16), (18), and (12), we have
()
where .
Now, by substituting (17)–(21) into (14), we obtain
()
Then, from Lemma  3.5 in [20] we have
()
()
()
Therefore we can reduce (22) by (23)–(25) as
()
Finally, we obtain the following nonlinear system of algebraic equation:
()
such that by solving this system we can obtain the vector C. Then, we can get
()

5. Convergence Analysis

In this section, we investigate the convergence analysis for the method presented in Section 4.

The problem (14) changes to the following problems
()
since
()
By taking we obtain the following fractional integral equation:
()
If we use the approximation u(t)≈CTΦm(t), then the problem (31) from space C1[0, 1] reduces to the following problem in space :
()
Now, similar to Theorem  6.1 in [21], we propose the next theorem.

Theorem 6. Suppose that u*(t) ∈ C1[0, 1] is the exact solution of (31) and , where

()
Then one has μm → 0 as  m → ∞ (i.e.,  um(t) → u*(t) as m → ∞).

Proof. By substituting (33) instead of (41) in [21], we can use the proof of Theorem  6.1 in [21].

Theorem 7. Suppose that u*(t) ∈ C1[0, 1] is the exact solution of (31) and um(t) ∈ Sm is the obtained solution of (26). Then one has um(t) → u*(t) as  m → ∞.

Proof. Substituting (17), (19), (20), and (12) in (32) we have

()
From Lemmas 2.3 and  4.1 in [21], we have as M → ∞. So we can observe that as M increases, (34) gets close to (32). Now, by taking M = m we propose the following problem that gets close to (32) as m increases:
()
Then by (23) and (25), (35) reduces to the following equation:
()
Equation (36) gets to (35) as M → ∞, because from Lemma  3.1 in [21] as M → ∞. Then by deleting , , taking M = m, and using (24) in (36), we have
()
where, from Lemma  3.1 in [21], as M → ∞. Now, by taking M = m and deleting in (37), we get (26). Obviously, if is solution of (32), then we have  −  um→0 as m → ∞.

On the other hand, from Theorem 6 we obtained as m → ∞. Therefore we can write um → u* as m → ∞ and the proof is complete.

6. Illustrative Numerical Examples

In this section, we apply our method with m = 10 (BPs of degree m = 10) to solve the following examples. We define ym(t) and y(t) for the approximate solution and the exact solution, respectively.

Example 1. Consider the nonlinear Riccati differential equation [14]:

()
subject to the initial condition as y(0) = 0. The exact solution of the equation for α = 1 is given as
()
Numerical results compared to [14] are given in Table 1 and also Figure 1 shows the absolute error for our method for α = 1 and Figure 2 shows behavior y10(t) for different values of α.

Table 1. Numerical results for α = 1 and m = 10 in Example 1 with comparison to exact solution and [14].
t Exact

Present method

m = 10

 Reference [14]
0.1 0.099668 0.099668 0.099668
0.2 0.197375 0.197375 0.197375
0.3 0.291313 0.291313 0.291313
0.4 0.379949 0.379949 0.379944
0.5 0.462117 0.462117 0.462078
0.6 0.537050 0.537050 0.536857
0.7 0.604368 0.604368 0.603631
0.8 0.664037 0.664037 0.661706
0.9 0.716298 0.716298 0.709919
1 0.761594 0.761594 0.746032
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Behavior of the absolute error function in Example 1 for α = 1 and m = 10.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Behavior of y10(t) in Example 1 for different α and exact solution for α = 1.

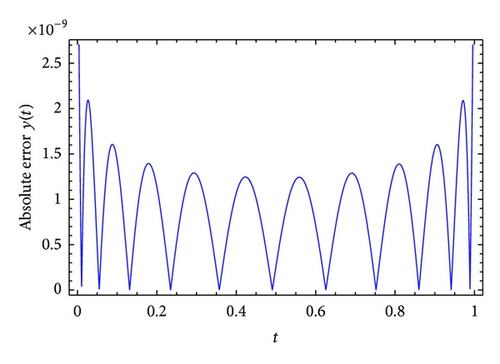
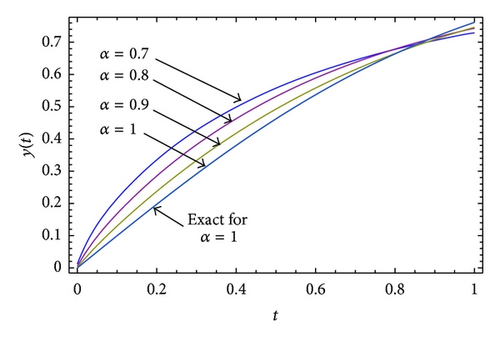
Example 2. Consider the following quadratic Riccati differential equation of fractional order [14]

()
subject to the initial condition as y(0) = 0. The exact solution of the equation for α = 1 is given as
()
Numerical results compared to [14] are given in Table 2 and also, Figure 3 shows the absolute error for our method for α = 1 and Figure 4 shows behavior y10(t) for different values of α.

Table 2. Numerical results for α = 1 and m = 10 in Example 2 with comparison to exact solution and [14].
t Exact

Present method

m = 10

 Reference [14]
0.1 0.110295 0.110295 0.110294
0.2 0.241977 0.241977 0.241965
0.3 0.395105 0.395105 0.395106
0.4 0.567812 0.567812 0.568115
0.5 0.756014 0.756014 0.757564
0.6 0.953566 0.953566 0.958259
0.7 1.152949 1.152949 1.163459
0.8 1.346364 1.346364 1.365240
0.9 1.526911 1.526911 1.554960
1 1.689499 1.689499 1.723810
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Behavior of the absolute error function in Example 2 for α = 1 and m = 10.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Behavior of y10(t) in Example 2 for different α and exact solution for α = 1.

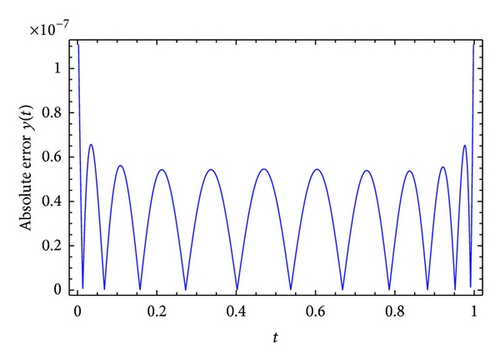
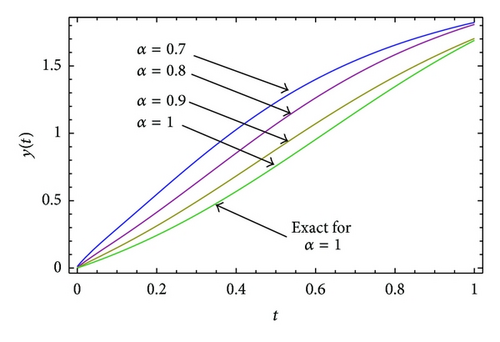
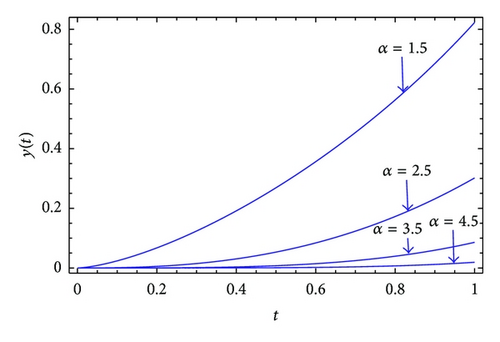
Example 3. Consider the nonlinear fractional differential equation:

()
with the initial conditions
()
This problem has been studied by using ADM [25], FDTM [26], and BPFs [27]. Our results with α = 1.5, α = 2.5 are compared to [25–27] in Tables 3 and 4. Therefore, we see that our method is very effective and obtained solutions that are in good agreement with the results in [25–27]. Also, Figure 5 shows behavior ym(t) for different values of α.

Table 3. Numerical results for α = 1.5 in Example 3 with comparison to [25–27].
t

Present method

m = 10

 ADM [25] FDTM [26] BPFs [27]
0.1 0.023779 0.023790 0.023790 0.023800
0.2 0.067336 0.067330 0.067330 0.067335
0.3 0.123886 0.123896 0.123896 0.123900
0.4 0.191373 0.191362 0.191362 0.191368
0.5 0.268851 0.268856 0.268856 0.268862
0.6 0.356235 0.356238 0.356238 0.356244
0.7 0.453958 0.453950 0.453950 0.453956
0.8 0.562999 0.563007 0.563007 0.563014
0.9 0.685066 0.685056 0.685056 0.685067
1 0.822540 0.822511 0.822509 0.822525
Table 4. Numerical results for α = 2.5 in Example 3 with comparison to [25, 26].
t

Present method

m = 10

 ADM [25] FDTM [26]
0.1 0.000952 0.000952 0.000952
0.2 0.005383 0.005383 0.005383
0.3 0.014833 0.014833 0.014833
0.4 0.030450 0.030450 0.030450
0.5 0.053197 0.053197 0.053197
0.6 0.083925 0.083925 0.083925
0.7 0.123412 0.123412 0.123412
0.8 0.172391 0.172391 0.172391
0.9 0.231574 0.231574 0.231574
1 0.301676 0.301676 0.301676
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Plot of y10(t) for different α in Example 3.

7. Conclusion

In this paper, we proposed a numerical method for solving the fractional quadratic Riccati differential equations by the operational matrices of the Bernstein polynomials. We applied operational matrix for fractional integration in the Riemann-Liouville sense. Then by using this matrix and operational matrix of product, we reduced the fractional quadratic Riccati differential equation to a system of algebraic equations that can be solved easily. Finally, examples have been simulated to demonstrate the high performance of the proposed method. We saw that the results were in good agreement with the analytical solutions and the solutions in the open literatures. Also, we observed that the solutions approach to classical solutions as the order of the fractional derivatives approaches 1, for fixed m.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.