Journal of Atomic and Molecular Physics
Volume 2013, Issue 1 451715
Research Article
Open Access

Generation of Multiple Focal Hole Segments Using Double-Ring Shaped Azimuthally Polarized Beam

K. Lalithambigai, 

K. Lalithambigai

Department of Physics, Periyar University, Salem, Tamilnadu 636 011, India periyaruniversity.ac.in

Search for more papers by this author
R. C. Saraswathi, 

R. C. Saraswathi

Department of Physics, Periyar University, Salem, Tamilnadu 636 011, India periyaruniversity.ac.in

Search for more papers by this author
P. M. Anbarasan, 

P. M. Anbarasan

Department of Physics, Periyar University, Salem, Tamilnadu 636 011, India periyaruniversity.ac.in

Search for more papers by this author
K. B. Rajesh, 

Corresponding Author

K. B. Rajesh

Department of Physics, Chikkanna Government Arts College, Trippur, Tamilnadu 641 602, India

Search for more papers by this author
Z. Jaroszewicz, 

Z. Jaroszewicz

Department of Physical Optics, Institute of Applied Optics, 04894 Warsaw, Poland inos.pl

National Institute of Telecommunications, 04894 Warsaw, Poland itl.waw.pl

Search for more papers by this author
First published: 05 June 2013
https://doi.org/10.1155/2013/451715
Citations: 8
Academic Editor: Mark D. Havey

Abstract

We investigated the focusing properties of a double-ring-shaped azimuthally polarized beam tightly focused with a high NA lens and a binary phase filter. We observe that by using 3 belts and 5 belts binary phase filters novel focal patterns including splitting of focal rings and multiring focus are obtained. We also found that a suitably designed phase structure can shift the focal rings along optical axis. The author expects such investigation is worthwhile for optical manipulation and material processing technologies.

1. Introduction

Growing interest in the generation of three-dimensional (3D) optical beams that are dark regions in space surrounded by light is driven by wide ranging applications including dark optical traps for atoms [1], manipulation, guiding and binding of microparticles and biological cells [2], and erase beams for super-resolution fluorescence microscopy [3]. Such beams are also known as twice-closed tubular optical structure (TCTOS) [4], optical bubbles [5], and hollow dark spherical spots [6]. Optical beams with oscillating on-axis intensity due to interference resulting in 3D intensity voids and 3D optical chains were proposed recently for trapping of multiple particles along the beam propagation and for controllable particle delivery [7]. Over the past years, a variety of techniques have been proposed for generating such optical bottle beams for applications in optical tweezers and atom traps [8–15]. Recently, a subwavelength focal hole (~0.5λ) with a quite long depth of focus (~48λ) is achieved near the focus by tight focusing of double-ring-shaped azimuthally polarized beam with high NA lens axicon [16]. In this paper we investigate the focal properties of the tightly focused azimuthally polarized double-ring-shaped beam using 3 belts and 5 belts binary phase filters. We observed that by properly designing the binary phase filters one can achieve many novel focal patterns including splitting of focal rings and generation of multiring structures.

2. Theoretical Work

A schematic diagram of the suggested method is shown in Figure 1. The analysis was performed on the basis of Richards and Wolf’s vectorial diffraction method [17] widely used for high-NA focusing systems at arbitrary incident polarization. In the case of the azimuthally incident polarization, adopting the cylindrical coordinates r,   z,   and  φ and the notations of [18], the electric field E(r, φ, z) in the vicinity of the focal region can be written as
()
Here A is relative amplitude, α = arcsin (NAmax /n) is the maximum aperture angle with (NAmax /n) is the numerical aperture, and n is the index of refraction between the lens and the sample. J1(x) denotes the Bessel functions of first order, and the function A (θ) describes the amplitude modulation.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
(Colour online) scheme for a double-ring-shaped azimuthally polarized beam focused by a binary phase plate with high NA lens. The red arrows in (a) shows the direction of polarization. (b) is the DOE and is placed near the lens approximately 1/4 the distance between lens and the source. The point Q(r,  z) in (c) represents the radial and axial coordinates of the observation point at the focal plane relative to the focus point, and φ is the azimuth angle defining the radial direction.
For illumination by a double-ring-shaped R-TEM11* beam with its waist in the pupil, this function is given by [19]
()
where β is the parameter that denotes the ratio of pupil diameter to the beam diameter and is the generalized Laguerre polynomial. If p = 1, the incident azimuthally polarized beam is a double-ring-shaped azimuthally polarized beam.

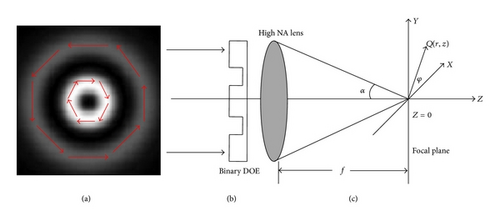
3. Analysis of Binary Phase Plate

It is seen from (1) that an additional radial electric field component is produced after introducing the phase modulation to the input double-ring-shaped azimuthally polarized beam [20]. Owing to this radial component, the polarization near the focal plane is rather complicated and space variant. We perform the integration of (1) numerically using parameters λ = 1, β = 1.3, and NAmax  of the objective is 0.9. Here, for simplicity, we assume that the refractive index n = 1 and A = 1. The effect of phase modulation on the input double-ring-shaped azimuthally polarized beam is evaluated by replacing the function A(θ) by A(θ)T(θ) where T(θ) for 3 belts binary phase plate (BPP) is given by
()
For 5-belt binary phase filter,
()

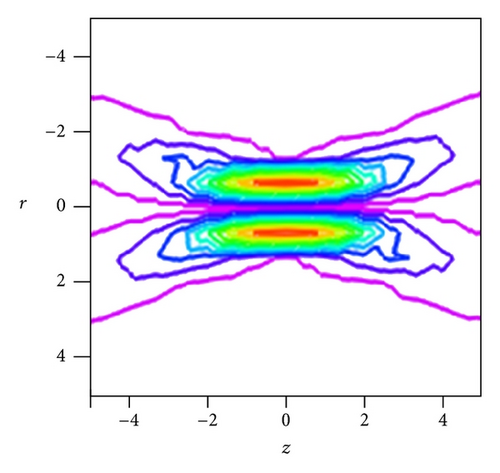
When a double-ring-shaped azimuthally polarized beam without any phase modulation is tightly focused, a single-ring focal hole pattern is obtained and is shown in Figure 2(a). We observed that the FWHM of the generated focal hole is 0.782λ and its corresponding focal depth is 4λ. Such a focal ring with subwavelength size can be used for stable trapping of single particle with low refractive index [21]. However, to trap two separates such particles and to manipulate them, we need to split this single-ring focal hole structure to a double ring structure. We observed that this is possible by introducing phase modulation to the input double-ring-shaped azimuthally polarized beam through a 3-belt binary phase plate. We optimized the NA of the first, second, and third ring of the 3-belt binary phase plate as NA1 = 0.1, NA2 = 0.25, and NAmax  = 0.9 for β = 1.35 to achieve the above-mentioned task, and the generated focal segment is shown in Figure 2(b). From Figure 2(b), we observed that the single focal hole is splitted into two focal holes, and the FWHM of each focal hole segment is measured as 0.468λ and is separated by the distance of 2.8λ between them. We observed that the residual intensity that exists between the two rings is only 35% of the total intensity measured at the focal hole. The ring focus altered by the BPP can be used to move the trapped particle from one place to another. We also observed that it is possible to increase the separation distance between the two focal rings by setting NA1 and NA2 of the BPP as 0.2, 0.85 and by tuning β = 1.5, respectively. The corresponding focal hole segment generated is shown in Figure 2(c). From the figure we measured that the FWHM of each focal holes is 0.468λ and is axially separated by the distance of 4λ between them. We observed that the residual intensity that exists between the two rings is only 33% of the total intensity measured at the focal hole. It is also possible to achieve 3-ring focal hole segment by setting NA1 and NA2 of the BPP as 0.3, 0.775 and by tuning β = 1.35. The corresponding focal hole segment generated is shown in Figure 2(d). From Figure 2(d), we measured that the FWHM of each focal hole is 0.468λ, and each of them is separated by the distance of 2.8λ. We observed that the residual intensity that exists between the rings is only 31% of the total intensity measured at the focal hole. We observed that by using 5 belts BPP, it is possible to generate double ring focal segments with FWHM of 0.468λ  and are axially separated by a large distance of 9.4λ  as shown in Figure 3(a).

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
(Colour online) shows the contour plot of the total intensity distribution in the yz plane near the focus for the focusing system with 3 belts BPF. (a) Single-ring focus, (b) double-ring focus, (c) double-ring focus with large separation of axial distance, and (d) triple-ring focus.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
(Colour online) shows the contour plot of the total intensity distribution in the yz plane near the focus for the focusing system with 3 belts BPF. (a) Single-ring focus, (b) double-ring focus, (c) double-ring focus with large separation of axial distance, and (d) triple-ring focus.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
(Colour online) shows the contour plot of the total intensity distribution in the yz plane near the focus for the focusing system with 3 belts BPF. (a) Single-ring focus, (b) double-ring focus, (c) double-ring focus with large separation of axial distance, and (d) triple-ring focus.
Details are in the caption following the image
Figure 2 (d)
Open in figure viewerPowerPoint
(Colour online) shows the contour plot of the total intensity distribution in the yz plane near the focus for the focusing system with 3 belts BPF. (a) Single-ring focus, (b) double-ring focus, (c) double-ring focus with large separation of axial distance, and (d) triple-ring focus.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
(Colour online) shows the contour plot of the total intensity distribution in the yz plane near the focus for the focusing system with 5-belt binary phase filters. (a) Double-ring focus and (b) four-ring focus.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
(Colour online) shows the contour plot of the total intensity distribution in the yz plane near the focus for the focusing system with 5-belt binary phase filters. (a) Double-ring focus and (b) four-ring focus.

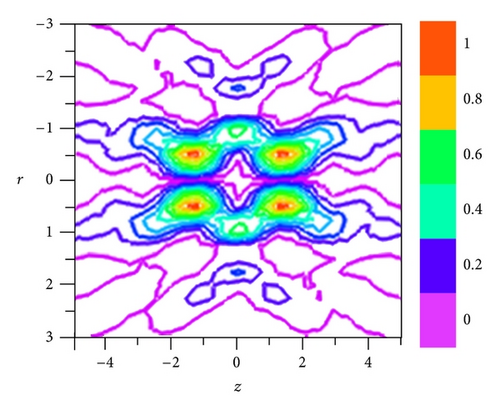
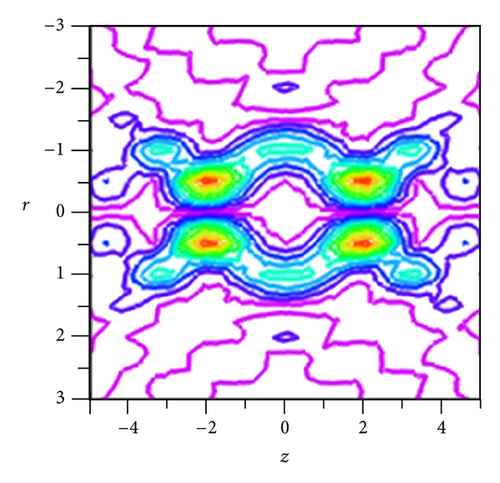
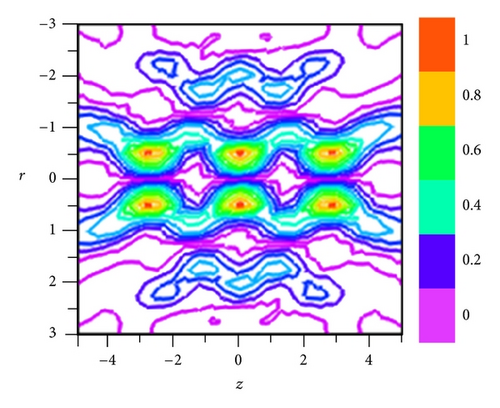
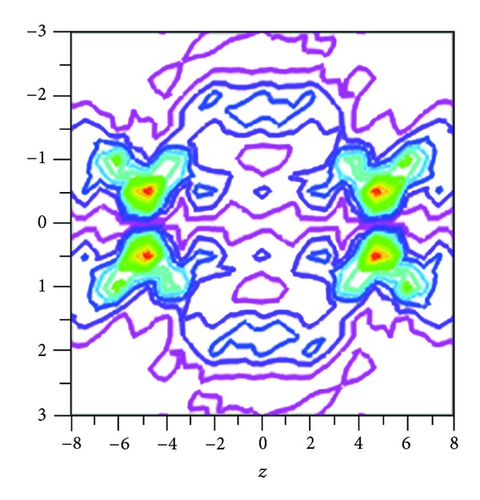
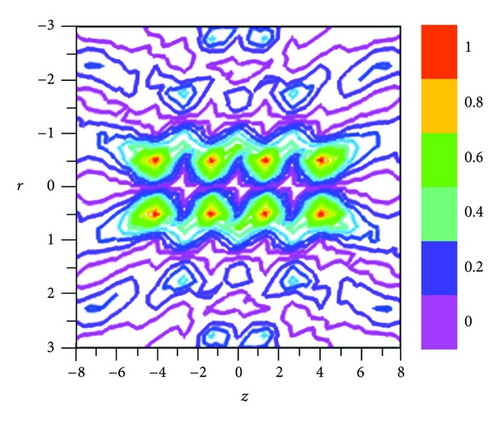
The set of values of NA of BPP optimized to achieve the above-mentioned task is NA1 = 0.34, NA2 = 0.57, NA3 = 0.78, NA4 = 0.85, and NAmax  = 0.9 for β = 1.36. From Figure 3(b) we also found that it is possible to generate four-ring patterns having almost uniform FWHM of 0.468λ and are axially separated by the distance of 2.7λ between them by setting NA1 = 0.24, NA2 = 0.354, NA3 = 0.6, NA4 = 0.8, and NAmax  = 0.9 for β = 1.3. We observed that the residual intensity that exists between the rings is only 30% of the total intensity measured at the focal hole. Thus with the help of liquid crystal-based tunable BPP, it is possible to generate tunable subwavelength focal hole segment with input double-ring-shaped azimuthally polarized beam.

4. Conclusion

In conclusion, we show by vector diffraction theory that the tight focusing of double-ring-shaped azimuthally polarized beam with a high NA lens and tunable BPP, it is possible to generate many novel focal patterns which are potentially useful for optical trapping and manipulation of low refractive index particles.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.