Volume 2013, Issue 1 428327

Research Article

Open Access

On a Five-Dimensional Chaotic System Arising from Double-Diffusive Convection in a Fluid Layer

R. Idris

Department of Mathematics, Faculty of Science and Technology, Universiti Malaysia Terengganu, 21030 Kuala Terengganu, Terengganu, Malaysia umt.edu.my

Search for more papers by this author

Z. Siri,

Z. Siri

Institute of Mathematical Sciences, University of Malaya, 50603 Kuala Lumpur, Malaysia um.edu.my

Search for more papers by this author

I. Hashim,

Corresponding Author

I. Hashim

[email protected]

School of Mathematical Sciences , Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia ukm.my

Search for more papers by this author

R. Idris,

R. Idris

Department of Mathematics, Faculty of Science and Technology, Universiti Malaysia Terengganu, 21030 Kuala Terengganu, Terengganu, Malaysia umt.edu.my

Search for more papers by this author

Z. Siri,

Z. Siri

Institute of Mathematical Sciences, University of Malaya, 50603 Kuala Lumpur, Malaysia um.edu.my

Search for more papers by this author

I. Hashim,

Corresponding Author

I. Hashim

[email protected]

School of Mathematical Sciences , Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia ukm.my

Search for more papers by this author

First published: 07 March 2013

https://doi.org/10.1155/2013/428327

Citations: 4

Academic Editor: Patricia J. Y. Wong

Share a link

Email
Wechat
Bluesky

Abstract

A chaotic system arising from double-diffusive convection in a fluid layer is investigated in this paper based on the theory of dynamical systems. A five-dimensional model of chaotic system is obtained using the Galerkin truncated approximation. The results showed that the transition from steady convection to chaos via a Hopf bifurcation produced a limit cycle which may be associated with a homoclinic explosion at a slightly subcritical value of the Rayleigh number.

1. Introduction

The concept of sensitivity on initial conditions where a small difference on initial conditions may produce large variations in the long-term behaviour of the system is pivotal in chaos theory. This behaviour is also known as the “butterfly effect” related to work done by Lorenz [1] where it is already described by Henri Poincare in 1890 in the literature in a particular case of the three-body problem. Chaotic behaviour has been studied intensively in various dynamical systems; see, for example, [2–14].

The investigation of free convection in the Rayleigh-Bénard problem is receiving much attention due to its wide application in different disciplines such as biotechnology for the description of the convection with the microorganisms diffusion, in astrophysics for simulation of the influence of the helium diffusion on convective motions in the stars, in oceanography for the investigation of the salinity influence on the convective motions in the seas, and in engineering and geology. Research in double-diffusive convection begins after the work done by sea-going oceanographers in order to measure the fluctuation of temperature and salinity as a function of depth as stated in the paper of Huppert and Turner [15]. Then, Knobloch et al. [16] and Bhattacharjee [17] studied the transition to chaos in double-diffusive convection with stress-free boundary conditions where oscillatory solution exists. They showed that the instability of fluid becomes oscillatory when thermal Rayleigh number is raised and the truncated model suggests that the appearance of chaos is associated with heteroclinic bifurcations.

Two-dimensional thermosolutal convection between free boundaries was studied numerically by Veronis [18]. From their observation, they found that when the solutal Rayleigh number is large enough, the oscillations underwent a bifurcation to asymmetry as thermal Rayleigh number increased and, for the larger values of solutal Rayleigh number, the transition from chaos to steady motion occurs.

Sibgatullin et al. [19] studied some properties of two-dimensional stochastic regimes of double-diffusive convection in a plane layer. Using the Bubnov-Galerkin method, they obtained that, with the growth of Rayleigh numbers of heat and salinity, the structure of one-dimensional curve becomes more irregular and sophisticated. Transition to chaos in double-diffusive Marangoni convection was studied by Li et al. [20]. It was found that the supercritical solution branch takes a quasiperiodicity and phase locking route to chaos while the subcritical branch follows the Ruelle-Takens-Newhouse scenario. The transitions from regular to chaotic dynamics and analysis of the hyper, hyper-hyper, and spatial-temporal chaos using the Lyapunov exponents of continuous mechanical systems have been studied in [21–24]; they found the Sharkovskii windows of periodicity in the systems investigated.

The objective of the present paper is to study the weak turbulence and chaos in double-diffusive convection involving temperature and concentration as the thermal Rayleigh number increases with rigid, no-slip horizontal boundary condition. Applying the truncated Galerkin approximation to the governing equations yields an autonomous system with five ordinary differential equations which can be used to understand low-dimensional dynamics before moving to studying more complex systems.

2. Mathematical Formulation

Consider a two-dimensional layer of fluid of depth H subject to gravity and heated from below as shown in Figure 1. A Cartesian coordinate system is used such that the vertical axis z is collinear with gravity, that is,

. The two long walls are maintained at temperatures T_H and T_C and solute concentrations S_H and S_C, respectively. A relationship between density, temperature, and solute concentration is assumed linear and can be presented by the following form ρ = ρ₀[1 − α(T − T_C) + α_s(S − S_C)], where α and α_s are volume expansion coefficients due to variations of thermal and solute concentrations. The Boussinesq approximation is applied for the effects of density variations for the gravity term in momentum equation. Therefore, the set of equations governing the conservation of mass, momentum, energy, and concentration for fluid flow is given by the following:

()

We nondimensionalize (1)–(4) using the following transformations:

()

where V_* = (u_*, v_*, w_*) is the velocity component, p_* is the pressure, (T − T_C) and (S − S_C) are the temperature and solute concentration variations, η_* is the effective thermal diffusivity, and ν_* is fluid’s viscosity.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Physical model.

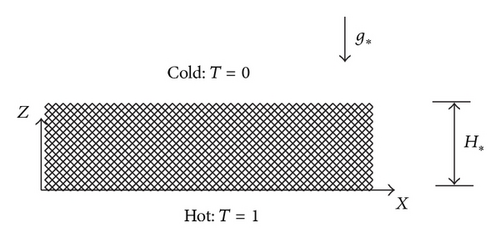
In this model, all the boundaries are rigid and the solution must follow the impermeability conditions there, that is, on the boundaries, where is a unit vector normal to the boundary. The temperature and solute concentration boundary conditions are T = S = 1 at z = 0 and T = S = 0 at z = 1.

For convective rolls having axes parallel to the shorter dimension (i.e., y = 0) v = 0, by applying the curl operator on (2) to eliminate the pressure and introducing the stream function defined by u = ∂ψ/∂z and w = −∂ψ/∂x, we get

()

where

()

which are, respectively, the Prandtl number, the Rayleigh number, the solutal Rayleigh number, and the Lewis number. The boundary conditions for the stream function are ψ = 0 on the horizontal boundaries. Equation (6) forms a nonlinear coupled system which together with the corresponding boundary conditions allows for a basic motionless conduction solution.

3. Diminished Set of Equation

In order to obtain the solution to (6), we represent the stream function, temperature, and solutal distributions in the following form:

()

Substituting (8) into (6), multiplying the equations by the orthogonal eigenfunctions corresponding to (8), and then integrating them over the spatial domain yield a set of five ordinary differential equations for the time evolution of the following amplitudes:

()

In (9), the time, the amplitudes, the Rayleigh number, and the solutal Rayleigh number were rescaled, and the following notations are introduced as follows:

()

Rescaling the equation again in the forms

()

gives the following set of scaled equations which are equivalent to (9):

()

where the dots (·) denote time derivatives d()/dτ.

4. Linear Stability Analysis

In this paper, we investigate the chaotic behaviour with low Prandtl number in double-diffusive convection. We obtained system (12) that provides a set of nonlinear equations with five parameters. The value of λ has to be consistent with the wave number at the convection threshold, a requirement for the convection cells to fit into the domain and fulfill the boundary conditions. However, the Lorenz equations have been extensively analyzed and solved for parameter values corresponding to convection in pure fluids and, even there, the parameter values most regularly used correspond to Pr = 10 and λ = 8/3. Therefore, it is of interest to analyze and solve the corresponding equations for parameter values corresponding to the problem under investigation. We employ the MATLAB ODE45 routine for obtaining the numerical solutions.

Before attempting the numerical solution of system (12), it is useful to examine the local stability of equilibrium points. System (12) has the three basic properties which we will discuss in the following: dissipation, fixed points, and stability of fixed points.

4.1. Dissipation

System (12) is dissipative since

()

Therefore, if the set of initial points in the phase space occupies region

at τ = 0, then, after some time, τ, the endpoints of the corresponding trajectories will fill a volume

()

The expression indicates that the volume decreases monotonically with time.

4.2. Fixed Points

The fixed points for velocity, temperature, and solute concentration can be obtained by setting the derivatives of system (12) to zero:

()

There is one trivial solution, that is, the origin in the phase space

()

which corresponds to the motionless solution. The other nonzero fixed points are given by the following:

()

where

()

The system has five fixed points. When R = 0, the five fixed points are all real. Thus, when (R − 1) > 0, h₁ is always real and h₂ and h₃ are always complex; therefore, the three fixed points (X_i, Y_i, U_i) are all complex and the other two fixed points, (Z_i, W_i), are all real for i = 2, …, 5. The fixed point (X₁, Y₁, Z₁, U₁, W₁) corresponds to motionless solution and (X_i, Y_i, Z_i, U_i, W_i), where i = 2, …, 5 corresponds to the convective solution.

4.3. Stability of the Fixed Points

The Jacobian matrix of (12) can be written as follows:

()

Since the matrix is 5 × 5, it is hard to obtain the eigenvalues in a closed form. Hence, the numerical calculation can be performed to discuss the stability at the fixed point. The motionless solution loses stability and the convection solution takes over at the fixed point {X₁, Y₁, Z₁, U₁, W₁} with the critical value, R_c1. Numerical results for the value of R_c1, which corresponds to the onset of convection, is obtained for various values of Le and R_s with the value of parameters Pr = 10 and λ = 8/3 as shown in Figure 2. Increasing the values of Le and R_s increases the value of R_c1.

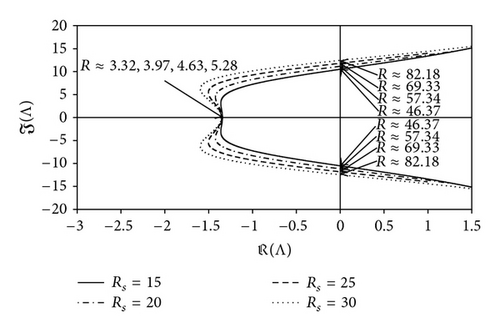
The stability of the fixed points (X_i, Y_i, Z_i, U_i, W_i) (i = 2, …, 5) is associated with the convective solution. The evolution of the complex eigenvalues of J in the case Pr = 10, λ = 8/3, and Le = 0.1 is plotted as shown in Figure 3(a) for the fixed point (X_4,5, Y_4,5, Z_4,5, U_4,5, W_4,5). These two roots become a complex conjugate at R≃ 3.32, 3.97, 4.63, and 5.28 for the case R_s = 15, 20, 25, and 30, respectively. At these points exactly, they still have negative real parts; therefore, the convection fixed points are stable, that is, spiral nodes. Of all the cases, both the imaginary and real parts of these two complex conjugate eigenvalues increase as R increases and they cross the imaginary axis on the complex plane, so as a result their real part becomes nonnegative at a value of R_c2≃46.37, 57.34, 69.33, 82.18. At these points, the convective fixed points lose their stability and another periodic, quasiperiodic or chaotic solution takes over. Figure 3(b) shows the evolution of the complex eigenvalues of J for the case Pr = 10, λ = 8/3 and R_s for the fixed point (X_4,5, Y_4,5, Z_4,5, U_4,5, W_4,5). These two roots become a complex conjugate at R≃3.33, 5.23, 7.03, 8.73 for the case of Le = 0.1, 0.2, 0.3, 0.4, respectively. As mentioned before, the convection fixed points are stable and become spiral nodes. Their real part becomes nonnegative at a value of R_c2≃31.71, 34.96, 40.05, 46.37. Therefore, at these points, the convective fixed points lose their stability and another periodic, quasiperiodic, or chaotic solution takes over.

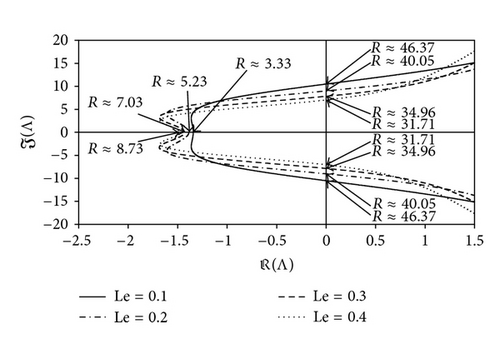
While for the fixed point (X_2,3, Y_2,3, Z_2,3, U_2,3, W_2,3), the evolution of the complex eigenvalues of J with the same parameter values is always on the positive side of Re(Λ), does not cross the zero axis for Re(Λ), and is not of interest in this study.

5. Results and Discussion

5.1. Bifurcations and Transition to Chaos

In this study, we focused on the dynamic behaviour of thermal convection in double-diffusive fluid layer. The values of Pr and λ used in all computations are 10 and 8/3, respectively, which are consistent with the critical Rayleigh number (R_c≃24.74) and the critical wave number at marginal stability in fluid layer convection. All solutions were obtained using the same initial conditions, which were selected to be in the neighborhood of the positive convection fixed point. The initial conditions are at τ = 0 : X, Y, Z, U, W = 0.9. All computations were carried out with the value of maximum time, τ_max = 210, and a step size Δτ = 0.001 using the built-in ODE45 method in MATLAB R2010a.

The bifurcation diagrams illustrated in Figure 4 show the peaks and valleys in the posttransient values of Z versus R. In Figure 4(a), for 0 < R < 46.37 we have one-point attractors, but the “attracted” value of Z increases as R increases, at least to R≃46.37. Bifurcation occurs at R≃46.37,48 until just beyond R = 50, where the system is chaotic. However, the system is not chaotic for all values of R > 50, and we will discuss it using phase-portrait diagram. When we fix Le = 0.1 and increase R_s from 15 to 30, the range of one-point attractor changes to 0 < R < 82.31; this is shown in Figure 4(b), while in Figure 4(c), one-point attractor dropped to 0 < R < 31.86 in the case of Le = 0.4 and R_s = 15. Here we can conclude that increasing the value of the solutal Rayleigh number (with fixed value of Lewis number) will delay the convection process. But increasing the value of Lewis number (with fixed value of solutal Rayleigh number) will enhance the onset of chaos.

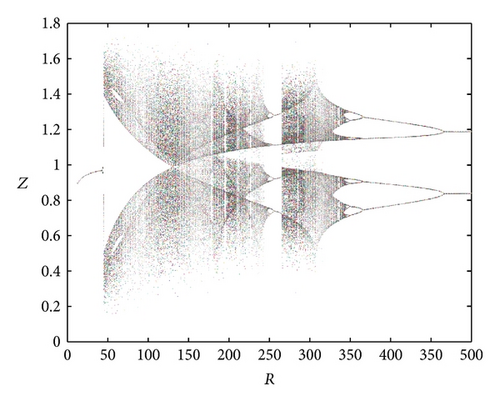
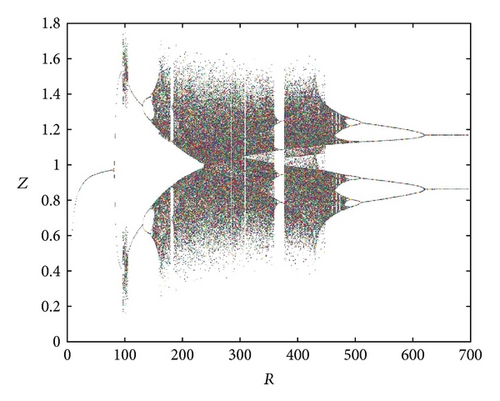
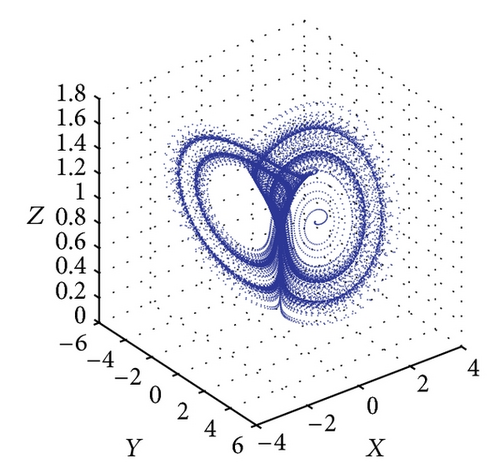
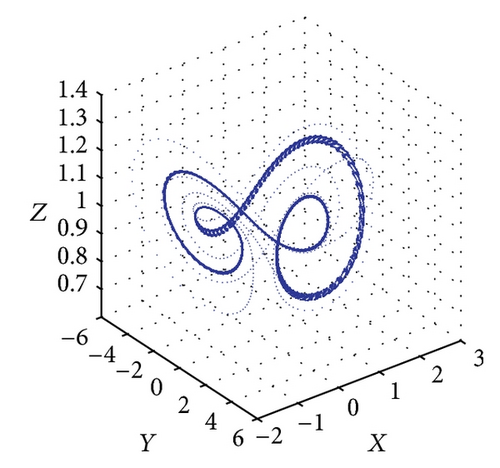
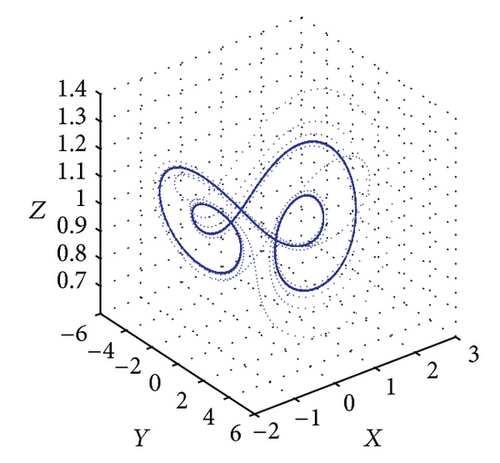
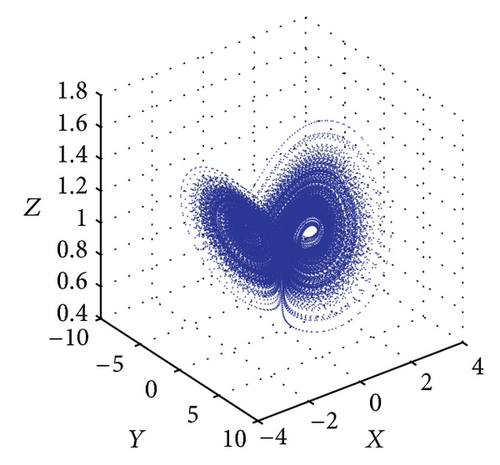
Figure 5 shows the projections of the trajectory’s data points on the X-Y-Z plane for Le = 0.1 and R_s = 15. From Figure 5(a), we obtain a solitary limit cycle signifying the loss of stability of the steady convective fixed points. The subcritical value for this transition is R_c2 = 46.37. Figure 5(b) shows the projections of the trajectory’s data points for R = 48. At this point, the homoclinic explosion occurs and the chaotic regime with the strange attractor takes over. The homoclinic explosion behaviour giving birth to a stable periodic orbit with period-8 at R = 250 is presented in Figure 5(c). This corresponds to the first wide periodic window within the chaotic regime. In Figure 5(d) we can observe that the data points do align in such a way as to produce an almost clear projection of unconnected points on the projected plane. Increasing the value of R further shows the dynamical behaviour’s return to being chaotic again at R = 300 as shown in Figure 5(e). At R = 360 and R = 400, we have a period-8 and period-4 periodic solutions as shown in Figures 5(f) and 5(g). Figure 5(h) shows that a period-2 periodic solution takes over at R = 500 and a period-2 periodic type remains when the solutions at higher values of R are obtained. We conclude the observation around these regimes of periodic windows within the broadband of chaotic solutions by pointing out a sequence of period-halving as one increases the Rayleigh number.

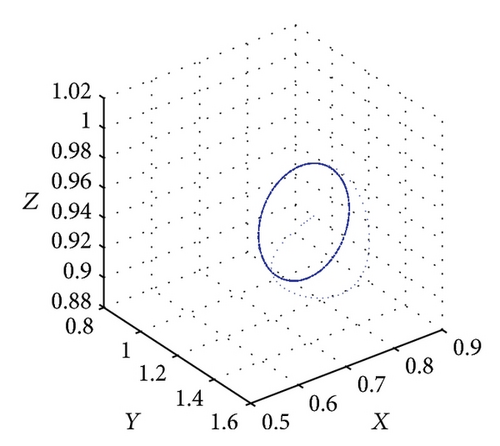
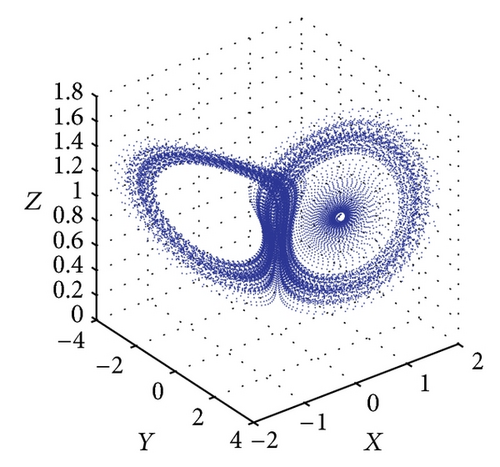
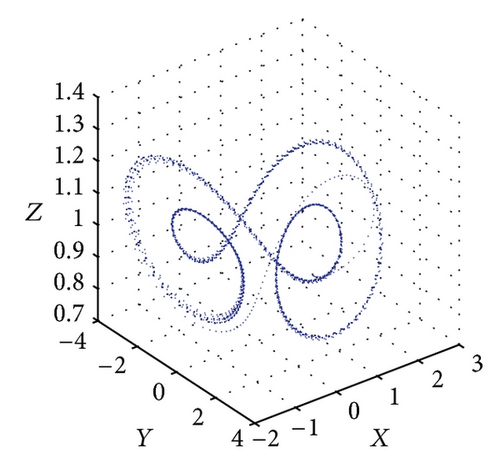
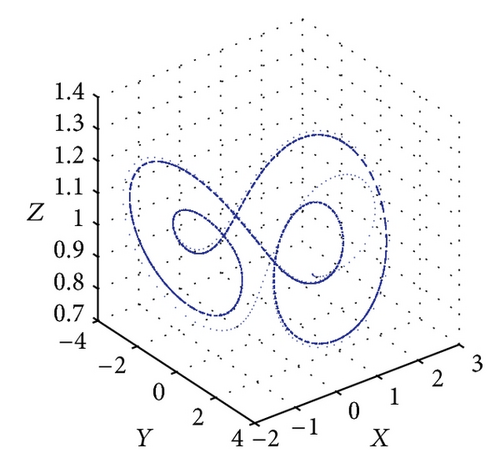
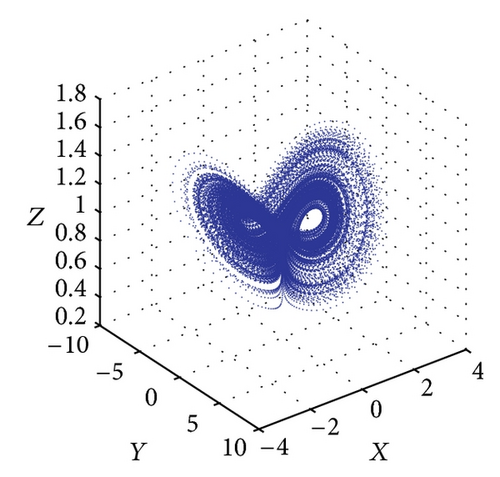
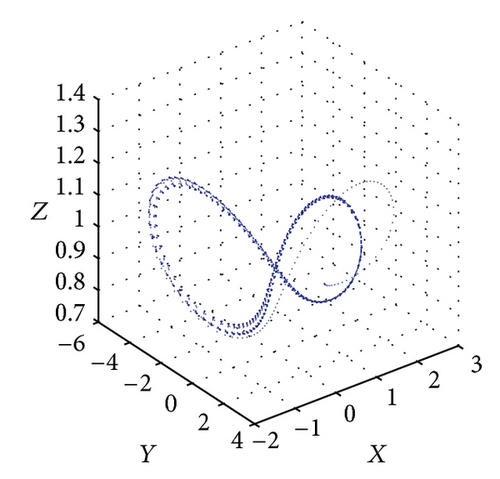
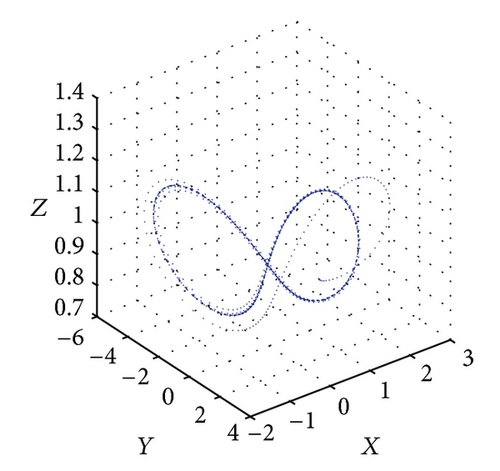
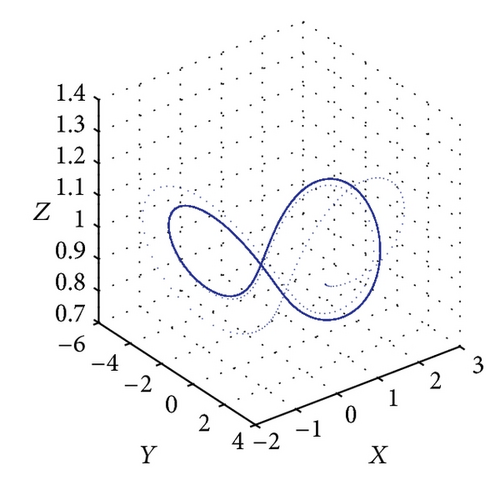
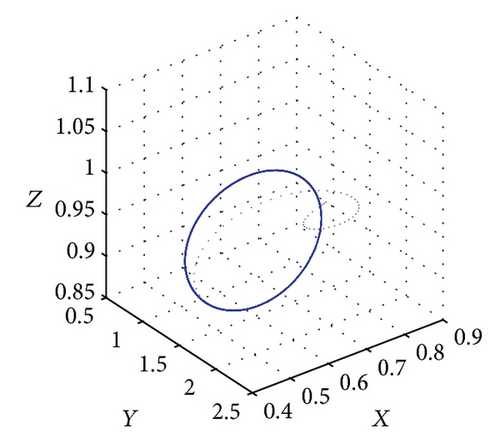
Figure 6 shows the projections of the trajectory’s data points on the X-Y-Z plane for Le = 0.1 and R_s = 30. The subcritical values for limit cycle and homoclinic explosion occur at R_c2 = 82.18 and R = 98 as shown in Figures 6(a) and 6(b), respectively, while period-8 is observed at R = 364 and 370 as presented in Figures 6(c) and 6(d). The dynamical behaviour returns to being chaotic again as R increases; this happens at R = 400 as shown in Figure 6(e). Figures 5(f) and 5(g) show a period-8 and period-4 periodic solutions at R = 490 and R = 500. Figure 6(h) shows that a period-2 periodic solution takes over at R = 600 and remains the same behaviour when the solutions at higher values of R are continued.

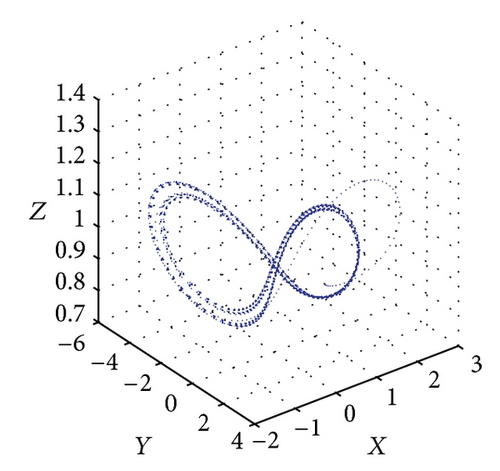
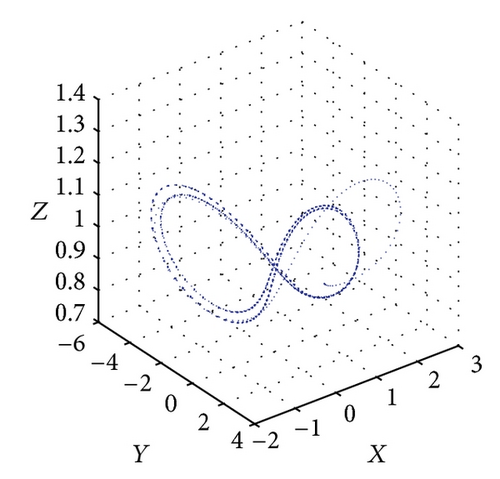
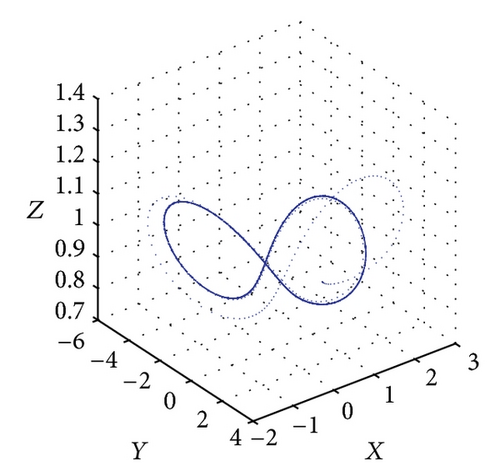
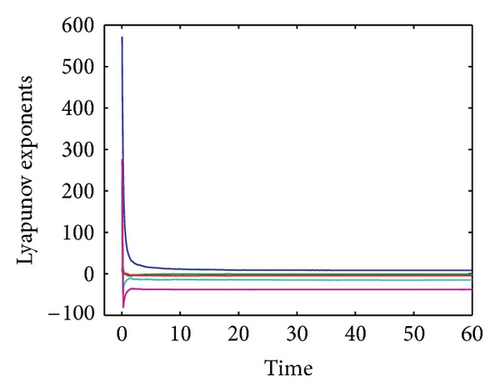
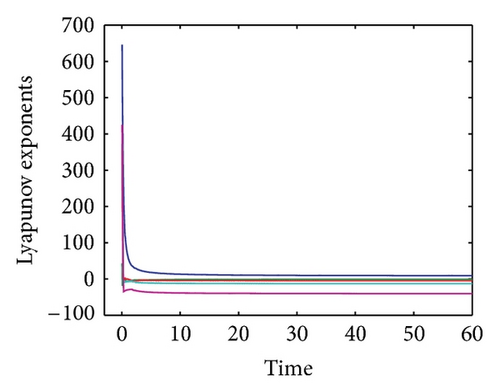
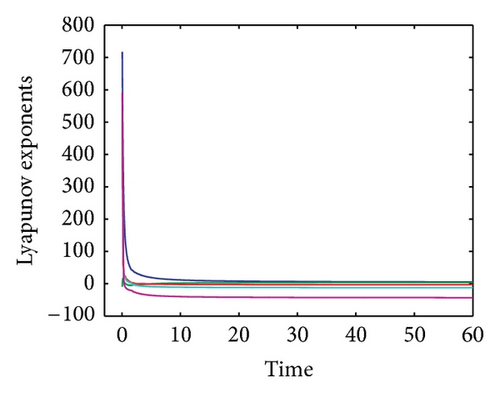
5.2. Lyapunov Exponents

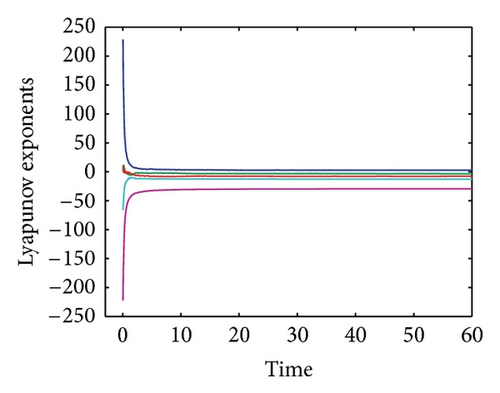
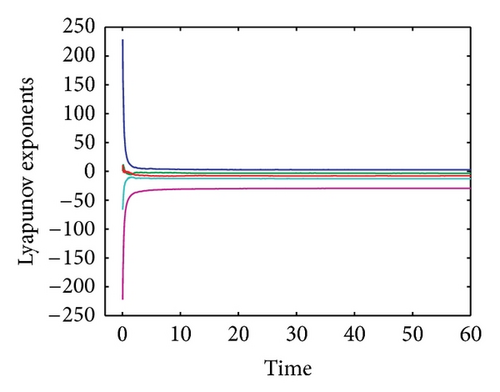
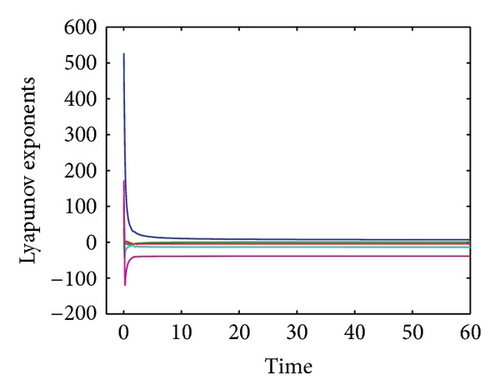
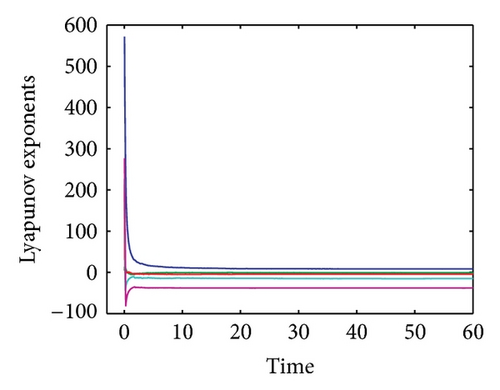
The convergence plot of the Lyapunov spectrum for system (12) is shown in Figure 7. The alogrithm as proposed by [24] was employed for this purpose. The values of the Lyapunov exponents for system (12) are tabulated in Table 1. From these results, we can conclude that for eigenvalue λ₁ the system is always unstable and chaotic with the increasing R. For λ₂, the system alternates between being stable and dissipative to unstable and chaotic when the value of R is increased. For eigenvalues λ₃, λ₄, and λ₅, the system is always stable and dissipative with the increasing R.

Table 1. Lyapunov exponents for system (12) computed from 10,000 data points for the case where Le = 0.1 and R_s = 15.

R	λ₁	λ₂	λ₃	λ₄	λ₅
46.37	2.674585	−3.572664	−7.683913	−12.847196	−28.904144
48	2.612254	−3.302684	−7.921422	−12.710783	−29.010697
260	6.350478	0.626358	−4.509057	−13.941471	−38.856433
300	7.469197	−0.458284	−4.653033	−14.610687	−38.076093
360	8.589279	0.219833	−4.754681	−15.043590	−39.338205
400	8.404066	−0.611687	−4.530720	−12.889258	−40.698489
500	4.451812	4.442320	−3.196173	−12.386501	−43.632794

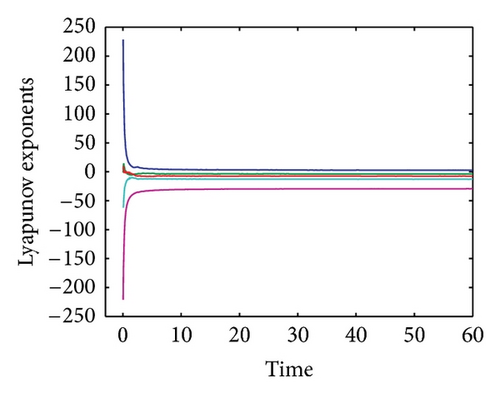
6. Conclusion

In this work, chaotic behaviour in double-diffusive convection in a fluid layer has been investigated. A five-dimensional model of chaotic system was obtained using the Galerkin truncated approximation. The transition from steady convection to chaos via a Hopf bifurcation produced a limit cycle which may be associated with a homoclinic explosion at a slightly subcritical value of the thermal Rayleigh number. Both the solutal Rayleigh number and Lewis number affect the stability of the system. Increasing the Rayleigh number shows that the trajectory of the data points pointing out a sequence of period-halving and the behaviour remains the same at a higher Rayleigh number. The different transitions of the system, can be implied by the different values of the Lyapunov exponents. Negative eigenvalues lead to a stable and dissipative system and positive eigenvalues show that the system is always unstable and chaotic, while alternate eigenvalues suggest different transitions of the system (i.e., stable and dissipative to unstable and chaotic) as the value of the Rayleigh number is increased.

Acknowledgments

The authors acknowledge the financial support from Universiti Malaysia Terengganu (Grant no. TPM-68006/2012/49), Universiti Kebangsaan Malaysia (Grant no. DIP-2012-12), and University of Malaya (Grant no. RG172-11AFR).

References

1 Lorenz E. N., Deterministic nonperiodic flow, Journal of the Atmospheric Sciences. (1963) 20, 130–141.
10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Web of Science® Google Scholar
2 Awrejcewicz J., Bifurcation and Chaos in Coupled Oscillators, 1991, World Scientific, Singapore, MR1178489, ZBL1160.65350.
10.1142/1342
Google Scholar
3 Awrejcewicz J. and Krysko V. A., Chaos in Structural Mechanics, 2008, Springer, Berlin, Germany, https://doi.org/10.1007/978-3-540-77676-5, MR2450642, ZBL1221.70027.
10.1007/978-3-540-77676-5
Google Scholar
4 Qi G., Du S., Chen G., Chen Z., and Yuan Z., On a four-dimensional chaotic system, Chaos, Solitons and Fractals. (2005) 23, no. 5, 1671–1682, https://doi.org/10.1016/j.chaos.2004.06.054, MR2101581, ZBL1071.37025.
10.1016/S0960-0779(04)00431-X
Web of Science® Google Scholar
5 Chen G. and Ueta T., Yet another chaotic attractor, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (1999) 9, no. 7, 1465–1466, https://doi.org/10.1142/S0218127499001024, MR1729683, ZBL0962.37013.
10.1142/S0218127499001024
Web of Science® Google Scholar
6 Liu W. B. and Chen G. A., A new chaotic system and its generation, International Journal of Bifurcation and Chaos. (2003) 13, 261–267.
10.1142/S0218127403006509
Web of Science® Google Scholar
7 Lü J. H., Chen G., Cheng D., and Celikovsky S., Bridge the gap between the Lorenz system and the Chen system, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2002) 12, no. 12, 2917–2926, https://doi.org/10.1142/S021812740200631X, MR1956411, ZBL1043.37026.
10.1142/S021812740200631X
Web of Science® Google Scholar
8 Chen Z. M. and Price W. G., On the relation between Rayleigh-Bénard convection and Lorenz system, Chaos, Solitons and Fractals. (2006) 28, no. 2, 571–578, https://doi.org/10.1016/j.chaos.2005.08.010, MR2178136, ZBL1084.76026.
10.1016/j.chaos.2005.08.010
CAS Web of Science® Google Scholar
9 Ookouchi Y. and Hada T., Chaotic convection in a simple system modified by differential heating, Journal of the Physical Society of Japan. (1997) 66, 369–378.
10.1143/JPSJ.66.369
CAS Web of Science® Google Scholar
10 Vadasz P., Local and global transitions to chaos and hysteresis in a porous layer heated from below, Transport in Porous Media. (1999) 37, no. 2, 213–245, https://doi.org/10.1023/A:1006658726309, MR1777372.
10.1023/A:1006658726309
Web of Science® Google Scholar
11 Vadasz P., Subcritical transitions to chaos and hysteresis in a fluid layer heated from below, International Journal of Heat and Mass Transfer. (2000) 43, 705–724.
10.1016/S0017-9310(99)00173-8
Web of Science® Google Scholar
12 Idris R. and Hashim I., Effects of a magnetic field on chaos for low Prandtl number convection in porous media, Nonlinear Dynamics. (2010) 62, no. 4, 905–917, https://doi.org/10.1007/s11071-010-9773-8, MR2745951, ZBL1215.76087.
10.1007/s11071-010-9773-8
Web of Science® Google Scholar
13 Mahmud M. N. and Hashim I., Effects of a magnetic field on chaotic convection in fluid layer heated from below, International Communications in Heat and Mass Transfer. (2011) 38, no. 4, 481–486.
10.1016/j.icheatmasstransfer.2010.12.023
Web of Science® Google Scholar
14 Jawdat J. M., Hashim I., and Momani S., Dynamical system analysis of thermal convection in a horizontal layer of nanofluids heated from below, Mathematical Problems in Engineering. (2012) 2012, 13, https://doi.org/10.1155/2012/128943, 128943.
10.1155/2012/128943
Web of Science® Google Scholar
15 Huppert H. E. and Turner J. S., Double-diffusive convection, Journal of Fluid Mechanics. (1981) 106, 299–329.
10.1017/S0022112081001614
Web of Science® Google Scholar
16 Knobloch E., Moore D. R., Toomre J., and Weiss N. O., Transitions to chaos in two-dimensional double-diffusive convection, Journal of Fluid Mechanics. (1986) 166, 409–448, https://doi.org/10.1017/S0022112086000216, MR850357, ZBL0612.76047.
10.1017/S0022112086000216
CAS Web of Science® Google Scholar
17 Bhattacharjee J. K., Convection and Chaos in Fluids, 1987, World Scientific, Singapore, MR924576.
10.1142/0347
Google Scholar
18 Veronis G., Effect of a stabilizing gradient of solute on thermal convection, Journal of Fluid Mechanics. (1968) 34, 315–336.
10.1017/S0022112068001916
Web of Science® Google Scholar
19 Sibgatullin I. N., Gertsenstein S. Ja., and Sibgatullin N. R., Some properties of two-dimensional stochastic regimes of double-diffusive convection in plane layer, Chaos. (2003) 13, no. 4, 1231–1241, https://doi.org/10.1063/1.1615911, MR2018763, ZBL1080.76564.
10.1063/1.1615911
CAS PubMed Web of Science® Google Scholar
20 Li Y. S., Chen Z. W., and Zhan J. M., Double-diffusive Marangoni convection in a rectangular cavity: transition to chaos, International Journal of Heat and Mass Transfer. (2010) 53, 5223–5231.
10.1016/j.ijheatmasstransfer.2010.07.037
Web of Science® Google Scholar
21 Awrejcewicz J., Krysko V. A., Papkova I. V., and Krysko A. V., Routes to chaos in continuous mechanical systems. Part 1: mathematical models and solution method, Chaos, Solitons and Fractals. (2012) 45, 687–708.
10.1016/j.chaos.2012.01.016
Web of Science® Google Scholar
22 Krysko V. A., Awrejcewicz J., Papkova I. V., and Krysko A. V., Routes to chaos in continuous mechanical systems. Part 2: modelling transitions from regular to chaotic dynamics, Chaos, Solitons and Fractals. (2012) 45, 709–720.
10.1016/j.chaos.2012.02.001
Web of Science® Google Scholar
23 Awrejcewicz J., Krysko A. A., Papkova I. V., and Krysko A. V., Routes to chaos in continuous mechanical systems. Part 3: the Lyapunov exponents, hyper, hyperhyper and spatial-temporal chaos, Chaos, Solitons and Fractals. (2012) 45, 721–736.
10.1016/j.chaos.2012.02.002
Web of Science® Google Scholar
24 Wolf A., Swift J. B., Swinney H. L., and Vastano J. A., Determining Lyapunov exponents from a time series, Physica D. Nonlinear Phenomena. (1985) 16, no. 3, 285–317, https://doi.org/10.1016/0167-2789(85)90011-9, MR805706, ZBL0585.58037.
10.1016/0167-2789(85)90011-9
CAS Web of Science® Google Scholar

Citing Literature

All articles

On a Five-Dimensional Chaotic System Arising from Double-Diffusive Convection in a Fluid Layer

Abstract

1. Introduction

2. Mathematical Formulation

3. Diminished Set of Equation