Abstract and Applied Analysis
Volume 2013, Issue 1 378593
Research Article
Open Access

A Representation of the Exact Solution of Generalized Lane-Emden Equations Using a New Analytical Method

Omar Abu Arqub, 

Omar Abu Arqub

Department of Mathematics, Faculty of Science, Al Balqa Applied University, Salt 19117 , Jordan bau.edu.jo

Search for more papers by this author
Ahmad El-Ajou, 

Ahmad El-Ajou

Department of Mathematics, Faculty of Science, Al Balqa Applied University, Salt 19117 , Jordan bau.edu.jo

Search for more papers by this author
A. Sami Bataineh, 

A. Sami Bataineh

Department of Mathematics, Faculty of Science, Al Balqa Applied University, Salt 19117 , Jordan bau.edu.jo

Search for more papers by this author
I. Hashim, 

Corresponding Author

I. Hashim

School of Mathematical Sciences, Universiti Kebangsaan Malaysia, 43600 Bangi, Selangor, Malaysia ukm.my

Search for more papers by this author
First published: 08 July 2013
https://doi.org/10.1155/2013/378593
Citations: 79
Academic Editor: Massimo Furi

Abstract

A new analytic method is applied to singular initial-value Lane-Emden-type problems, and the effectiveness and performance of the method is studied. The proposed method obtains a Taylor expansion of the solution, and when the solution is polynomial, our method reproduces the exact solution. It is observed that the method is easy to implement, valuable for handling singular phenomena, yields excellent results at a minimum computational cost, and requires less time. Computational results of several test problems are presented to demonstrate the viability and practical usefulness of the method. The results reveal that the method is very effective, straightforward, and simple.

1. Introduction

Since the beginning of stellar astrophysics, the investigation of stellar structures has been a central problem. There have been continuous efforts to deduce the radial profiles of the pressure, density, and mass of a star, and one of the key results that came out of these efforts is the Lane-Emden equation, which describes the density profile of a gaseous star. Mathematically, the Lane-Emden equation is a second-order singular ordinary differential equation. In astrophysics, the Lane-Emden equation is essentially a Poisson equation for the gravitational potential of a self-gravitating, spherically symmetric polytropic fluid.

The Lane-Emden equation has been used to model several phenomena in mathematical physics, thermodynamics, fluid mechanics, and astrophysics, such as the theory of stellar structure, the thermal behavior of a spherical cloud of gas, isothermal gas spheres, and the theory of thermionic currents [9–13]. Lane-Emden-type equations were first published by Lane [14]; they were explored in more detail by Emden in 1870 [15], who considered the thermal behavior of a spherical cloud of gas that acts under the mutual attraction of its molecules and is subject to the classical laws of thermodynamics. The reader is kindly requested to peruse [9–17] to know more details about Lane-Emden-type equations, including their history, variations, and applications.

In the present paper, we introduce a simple new analytical method we call the residual-power-series (RPS) method [18] to discover series solutions to linear and nonlinear Lane-Emden equations. The RPS method is effective and easy to use to solve Lane-Emden equations without linearization, perturbation, or discretization. This method constructs an approximate analytical solution in the form of a polynomial. By using the concept of residual error, we obtain a series solution, which in practice tends to be a truncated series solution.

The RPS method has the following characteristics [18]: first, it obtains a Taylor expansion of the solution, and as a result, the exact solution is obtained whenever it is a polynomial. Moreover, the solutions and all of its derivatives are applicable for each arbitrary point in a given interval. Second, the RPS method has small computational requirements and high precision, and furthermore it requires less time.

In the present paper, the RPS method is used to obtain a symbolic approximate solution for generalized Lane-Emden equations in the following form that are assumed to have a unique solution in the interval of integration:
()
which is subject to both the initial conditions,
()
and one of the following constraint-conditions cases:
  •  

    case I: p1(x0) ≠ 0, q1(x0) = 0,

  •  

    case II:, q2(x0) = 0,

where f, g, h are nonlinear analytic functions, pi,  qi  are analytic functions on [x0, x0 + a], y(x)  is an unknown function of an independent variable  x  that is to be determined, and x0, ai, a ∈ ℝ with a > 0. Throughout this paper, we assume that y(x) is an analytic function on the given interval.

As special cases, when f(y′(x)) = y′(x), h(x, y(x), y′(x)) = h(x), p1(x) ∈ ℝ, q1(x) = x, q2(x) = 1, x0 = 0, and for special forms of g(y(x)), we obtain several well-known forms of the Lane-Emden equations. For example, when   g(y(x)) = (y(x))n, n ∈ ℕ, h(x, y(x), y′(x)) = 0, a0 = 1, and a1 = 0, we obtain the form of (1) and (2) that is the standard Lane-Emden equation; this equation was originally used to model the thermal behavior of a spherical cloud of gas that acts under the mutual attraction of its molecules and is subject to the classical laws of thermodynamics [10, 16]. However, when g(y(x)) = ey(x), h(x, y(x), y′(x)) = 0, a0 = 0, and a1 = 0, the obtained model can be used to view isothermal gas spheres, where the temperature remains constant [10, 17]. For a thorough discussion of the formulation of the Lane-Emden equations and the corresponding physical behavior of the modeled systems, the reader is referred to [9–17].

In most cases, the Lane-Emden equation does not always have solutions that can be obtained using analytical methods. In fact, many of real physical and engineering phenomena that are encountered are almost impossible to solve by this technique; hence, these problems must be attacked by various approximate and numerical methods. Therefore, some authors have proposed numerical methods to approximate the solutions of a special case of (1) and (2). For example, the Adomian decomposition method has been applied to solve the Lane-Emden equation y′′(x)+(β/x)y′(x) + f(y(x)) + g(x) = 0 as described in [3]. In [1], the authors developed the optimal homotopy asymptotic method to solve the singular equation y′′(x)+(β/x)y′(x) + f(y(x)) + h(x) = 0. Additionally, in [2], the authors provided the Hermite functions collocation method to further investigate the Lane-Emden equation y′′(x)+(β/x)y′(x) + p(x)f(y(x)) + g(x) = 0. Furthermore, the homotopy perturbation method is carried out in [4] to solve the equation y′′(x)+(β/x)y′(x) + f(y(x)) = 0. Recently, the Bessel collocation method was proposed to solve the linear Lane-Emden equation y′′(x)+(β/x)y′(x) + p(x)y(x) + f(x) = 0 in [19].

However, none of the previous studies propose a methodical way to solve (1) and (2). Moreover, the previous studies require more effort to achieve their results, and usually they are only suited for a special form of (1) and (2). However, the applications of other versions of series solutions to linear and nonlinear problems can be found in [20–25], and, to discern the numerical solvability of different categories of singular differential equations, one can consult [26].

The outline of the paper is as follows: in the next section, we present the formulation of the RPS method. Section 3 covers the convergence theorem. In Section 4, numerical examples are given to illustrate the capability of the proposed method. This paper ends in Section 5 with some concluding remarks.

2. The Formulation of the RPS Method

In this section, we employ the RPS method to find a series solution to the generalized Lane-Emden equation (1) that is subject to given initial conditions equation (2). First, we formulate and analyze the RPS method to solve such problems.

The RPS method consists of expressing the solution of (1) and (2) as a power-series expansion about the initial point x = x0. To achieve our goal, we suppose that these solutions take the form where ym are the terms of approximations ym(x) = cm(x − x0) m, m = 0,1, 2, ….

Obviously, when m = 0,1 because y0(x), satisfy the initial conditions (2) as y(x0) = c0 = y0(x0) and , we have an initial guess for the approximation of y(x), namely, yinitial(x) = y(x0) + y′(x0)(x − x0). In contrast, if we choose yinitial(x) as the initial guess for an approximation of y(x), then we can calculate ym(x) for m = 2,3, 4, … and approximate the solution y(x) of (1) and (2) by the following kth-truncated series:
()
Prior to applying the RPS method, we rewrite the singular equations (1) and (2) in the following form:
()
where P(x) = q1(x)q2(x), Q(x) = p1(x), U(x) = p2(x)q1(x) and V(x) = q1(x)q2(x). Substituting the  kth truncated series yk(x) into (4) leads to the following definition of the kth residual function:
()
and, furthermore, we obtain the following ∞th residual function Res∞(x) = lim k→∞Resk(x). It easy to see that Res∞(x) = 0 for each x ∈ [x0, x0 + a]. Thus, Res∞(x) is infinitely differentiable function at x = x0. Furthermore, (dk−1/dxk−1)Res∞(x0) = (dk−1/dxk−1)Resk(x0) = 0. In fact, this relation is a fundamental rule in the RPS method and its applications.
Now, in order to obtain the second approximate solution, we set k = 2 and . Then we differentiate both sides of (5) with respect to x and substitute x = x0 to obtain the following:
()
Using the facts that (d/dx)Res∞(x0) = (d/dx)Res2(x0) = 0 and that U(x0) = V(x0) = 0, we know that (6) gives the following value for c2:
()
Thus, using the second truncated series, the second approximate solution for (1) and (2) can be written as
()
Similarly, to find the third approximate solution, we set k = 3 and . Then we differentiate both sides of (5) with respect to x and substitute x = x0 to obtain the following value of c3:
()
The above result is valid due to the fact that (d/dx)Res3(x0) = 0. Hence, using the third truncated series, the third approximate solution for (1) and (2) can be written as
()

This procedure can be repeated till the arbitrary order coefficients of RPS solutions for (1) and (2) are obtained. Moreover, higher accuracy can be achieved by evaluating more components of the solution.

3. Convergence Theorem and Error Analysis

In this section, we study the convergence of the present method to capture the behavior of the solution. Afterwards, error functions are introduced to study the accuracy and efficiency of the method. Actually, continuous approximations to the solution will be obtained.

Taylor’s theorem allows us to represent fairly general functions exactly in terms of polynomials with a known, specified, and bounded error. The next theorem will guarantee convergence to the exact analytic solution of (1) and (2).

Theorem 1. Suppose that y(x) is the exact solution for (1) and (2). Then the approximate solution obtained by the RPS method is in fact the Taylor expansion of y(x).

Proof. Assume that the approximate solution for (1) and (2) is as follows:

()
In order to prove the theorem, it is enough to show that the coefficients cm in (11) take the form
()
where y(x) is the exact solution for (1) and (2). Clearly, for m = 0 and m = 1 the initial conditions (2) give c0 = y(x0) and c1 = y′(x0), respectively. Moreover, for m = 2, differentiate both sides of (4) with respect to x and substitute x = x0 to obtain
()
Indeed, from (11), one can write
()
By substituting (14) into (4), differentiating both sides of the resulting equation with respect to x, and then setting x = x0, we obtain
()
By comparing (13) and (15), it easy to see that c2 = (1/2!)y′′(x0). Hence, according to (14) the approximation for (1) and (2) is
()
Furthermore, for m = 3, differentiating both sides of (4) twice with respect to  x  and then substituting x = x0 yields the following result:
()
By substituting (16) into (4), differentiating both sides of the resulting equation twice with respect to x, and then setting x = x0, we obtain
()
By comparing (17) and (18), we can conclude that c3 = (1/3!)y′′′(x0). Thus, according to (16), we can write the approximation for (1) and (2) as
()
By continuing the above procedure, we can easily prove (13) for m = 4,5, 6, …. Thus, the proof of the theorem is complete.

Corollary 2. If y(x)  is a polynomial, then the RPS method will obtain the exact solution.

It will be convenient to have a notation for the error in the approximation y(x) ≈ yk(x). Accordingly, let Remk(x)  denote the difference between y(x)  and its kth Taylor polynomial, which is obtained from the RPS method; that is, let
()
The functions Remk(x)  are called the kth remainder of the RPS approximation of y(x). In fact, it often happens that the remainders Remk(x)  become smaller and approach zero as k approaches infinity. The concept of “accuracy” refers to how closely a computed or measured value agrees with the true value. To show the accuracy of the present method, we report three types of error functions. The first one is the exact error, Ext , which is defined as follows:
()
Similarly, the consecutive error, which is denoted by Con, and the residual error, which is denoted by Res, are defined by
()
respectively, where x ∈ [a, b] and yk(x) are the kth-order approximation of y(x) that is obtained by the RPS method. An excellent account of the study of error analysis, which includes its definitions, varieties, applications, and method of derivations, can be found in [27].

4. Numerical Results and Discussion

The proposed method provides an analytical approximate solution in terms of an infinite power series. However, there is a practical need to evaluate this solution and to obtain numerical values from the infinite power series. The consequent series truncation and the corresponding practical procedure are realized to accomplish this task. The truncation transforms the otherwise analytical results into an exact solution, which is evaluated to a finite degree of accuracy.

In this section, we consider six examples to demonstrate the performance and efficiency of the present technique. Throughout this paper, all of the symbolic and numerical computations are performed using the Maple 13 software package.

4.1. Example 1

Consider the following linear nonhomogeneous Lane-Emden equation:
()
which is subject to the initial conditions
()
As we mentioned earlier, if we select the first two terms of the approximations as y0(x) = 0 and y1(x) = 0, then the kth-truncated series has the form
()
To find the values of the coefficients cm, m = 2,3, 4, …, we employ our RPS algorithm. Therefore, we construct the residual function as follows:
()
Consequently, the 4th-order approximation of the RPS solution for (23) and (6) according to this residual function is as follows:
()
which agrees with Corollary 2. It easy to demonstrate that each of the coefficients cm for m ≥ 5 in expansion (25) vanishes. In other words, . Thus, the analytic approximate solution to (23) and (6) is identical to the exact solution y(x) = x4 − x3. Table 1 shows a comparison between the absolute errors of our method that were obtained from a 4th-order approximation, the optimal homotopy asymptotic method [1], and the Hermite functions collocation method [2]. From the table, it can be seen that the RPS method provides us with an accurate approximate solution to (23) and (6). In fact, the results reported in this table confirm the effectiveness and accuracy of our method.
Table 1. A numerical comparison of the exact error function Ext k(x) to Example 1 for different values of x in [0,10].
xi Exact solution Reference [1] Reference [2] Present method
0 0 0 0 0
0.01 −0.00000099 6.295572 × 10−19 5.790000 × 10−8 0
0.1 −0.0009 5.83469 × 10−13 8.409000 × 10−7 0
0.5 −0.0625 4.937685 × 10−9 2.195800 × 10−6 0
1 0 1.079378 × 10−8 8.284000 × 10−7 0
2 8 1.614569 × 10−4 1.732000 × 10−7 0
5 500 1.80785 × 10+2 1.909000 × 10−7 0
10 9000 1.894851 × 10+6 3.391999 × 10−4 0

4.2. Example 2

Consider the following nonlinear homogeneous Lane-Emden equation:
()
which is subject to the initial conditions
()
Assume that the initial guess approximation (which is the 1st approximation) has the form y1(x) = 1. Then, the 10th truncated series of the RPS solution of y(x) for (28) and (29) is as follows:
()
Thus, the exact solution of (28) and (29) has a general form that coincides with the exact solution
()

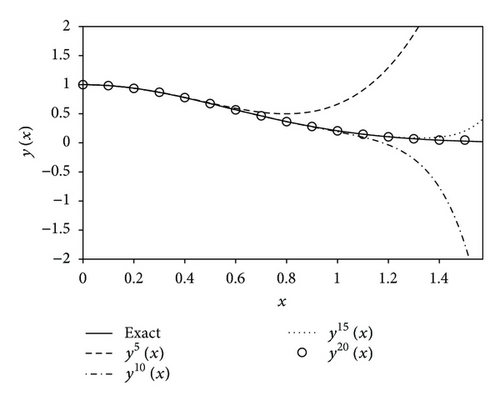
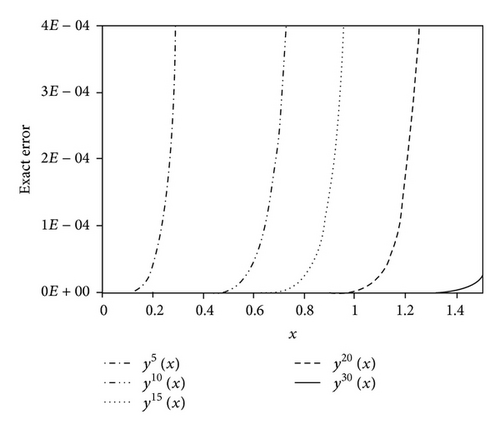
Let us carry out an error analysis of the RPS method for this example. Figure 1 shows the exact solution y(x) and the four iterated approximations yk(x) for k = 5,10,15,20. This graph exhibits the convergence of the approximate solutions to the exact solution with respect to the order of the solutions. In Figure 2, we plot the exact error functions Extk(x) when k = 5,10,15,20, 30, which approach the axis y = 0 as the number of iterations increases. This graph shows that the exact errors become smaller as the order of the solutions increases, that is, as we progress through more iterations. These error indicators confirm the convergence of the RPS method with respect to the order of the solutions. From Figure 2, it is easy for the reader to compare the new result of the RPS method with the exact solution. Indeed, this graph shows that the current method has an appropriate convergence rate.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Plots of the RPS solution to (28) and (29) when k = 5,10,15,20 and the exact solution is on [0, π/2].
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Plots of the exact error functions for (28) and (29) when k = 5,10,15,20 on [0, π/2].

4.3. Example 3

Consider the following nonlinear homogeneous Lane-Emden equation:
()
which is subject to the initial conditions
()
After we apply the RPS method to solve (32) and (33), we construct the residual function as follows:
()
where is the kth-truncated series that approximates the solution y(x). As we mentioned earlier, if we select the first two terms of the approximations as y0(x) = 0   and y1(x) = 0 (which would imply that c1 = c2 = 0), then the first few terms of the approximations of the RPS solution for (32) and (33) are
()
Furthermore, if we collect the above results, then the 10th-truncated series of the RPS solution for y(x) is given as
()
Thus, the exact solution of (32) and (33) has the general form that coincides with the exact solution
()

In most real-life situations, the Lane-Emden equation is too complicated to solve exactly, and, as a result, there is a practical need to approximate the solution. In the next two examples, the exact solution cannot be found analytically.

4.4. Example 4

Consider the following nonlinear homogeneous Lane-Emden equation:
()
which is subject to the initial conditions
()
As we mentioned earlier, if we select the initial guess approximation as y1(x) = 1, then the Taylor series expansion of the solution for (38) and (39) is as follows:
()
Consequently, the 10th-order approximation of the RPS solution for (38) and (39) is
()

Our next goal is to show how the kth value in the kth-truncated series (3) affects the approximate solutions. In Table 2, the residual error has been calculated for various values of x  in [0,2] to measure the extent of agreement between the kth-order approximate RPS solutions when k = 10,15,20,25. As a result, Table 2 illustrates the rapid convergence of the RPS method by increasing the orders of approximation. To show the efficiency of the RPS method, numerical comparisons are also studied. Table 3 shows a comparison of y(x) that is obtained by the 10th-order approximation of the RPS method with those results that were obtained by the Adomian decomposition method [3], the Hermite functions collocation method [2], and the homotopy perturbation method [4]. Again, we find that our method has a similar degree of accuracy to these other methods.

Table 2. The values of the residual error function Resk (x) to Example 4 when k = 10,15,20,25 for different values of x in [0,2].
  xi Res10(xi) Res15(xi) Res20(xi) Res25(xi)
0 0 0 0 0
0.1 4.528461 × 10−13 4.528461 × 10−13 4.528461 × 10−13 4.528461 × 10−13
0.2 1.250167 × 10−12 3.996803 × 10−15 3.996803 × 10−15 3.996803 × 10−15
0.5 1.785672 × 10−9 6.611378 × 10−14 1.045275 × 10−13 1.045275 × 10−13
1 3.539988 × 10−6 8.587641 × 10−9 4.061307 × 10−12 1.395550 × 10−13
1.5 2.884109 × 10−4 3.208217 × 10−6 1.902825 × 10−8 1.854792 × 10−10
2 6.215665 × 10−3 1.865257 × 10−4 7.253518 × 10−6 1.909733 × 10−7
Table 3. A numerical comparison of the approximate solution to Example 4 for different values of x in [0,2].
xi Reference [3] Reference [2] Reference [4] Present method
0 1 1 1 1
0.1 0.9985979358 0.9986051425 0.9985979358 0.9985979274
0.2 0.9943962733 0.9944062706 0.9943962733 0.9943962649
0.5 0.9651777886 0.9651881683 0.9651777886 0.9651777802
1 0.8636811027 0.8636881301 0.8636811027 0.8636811256
1.5 0.7050419247 0.7050524103 0.7050419247 0.7050452522
2 0.5063720330 0.5064687568 0.5063720330 0.5064651631

4.5. Example 5

Consider the following homogeneous nonlinear Lane-Emden equation:
()
which is subject to the initial conditions
()

Historically, this type of Lane-Emden equation was derived by Bonnor [28] in 1956 to describe what are now commonly known as Bonnor-Ebert [28, 29] gas spheres. These gas spheres are isothermal gas spheres that have been embedded in a pressurized medium at the maximum possible mass that allows a hydrostatic equilibrium. The derivation is based on earlier work by Ebert [29], and hence, the equation is often referred to as the Lane-Emden equation of the second kind (which depends on an exponential nonlinearity). For a derivation of the Lane-Emden equation of the second kind, the reader is kindly requested to peruse [30–33].

In fact, this model appears in Richardson’s theory of thermionic currents when the density and electric force of an electron gas in the neighborhood of a hot body in a thermal equilibrium [10] must be determined. For a thorough discussion of the formulation of (42) and (43) and the physical behavior of the emission of electricity from hot bodies, see [10, 11]. It should be observed that this equation is nonlinear and has no analytic solution.

As we mentioned earlier, if we select the initial guess approximation as y2(x) = 0, then the Taylor series expansion of solutions to (42) and (43) is as follows:
()
Consequently, the 10th-order approximation of the RPS solution for (42) and (43) according to this initial guess is
()
As in the previous example, exact solutions do not exist for the Lane-Emden equations (42) and (43). Thus, in Table 4 we compare our results to the results from the literature. Some of these results were obtained in [5] by constructing analytic approximations based on Euler transform series; others were obtained in [6] by using two acceleration methods to improve the convergence over the standard Taylor series results. In addition, the author in [7] applied the fractional approximation technique and the authors in [8] applied the Boubaker polynomials expansion scheme. In the above table, it can be seen that our results from the RPS method agree principally with the methods of [5, 7]. In addition, we find that our results agree well with method [6]. However, for small x, we find that the results of [8] agree well with the method of [7], and if x is larger, we find that these results agree with method [6]. This conclusion is reasonable, as the fractional-approximation-technique solution in [7] is of low order, and hence, it is valid for x close to x = 0. In contrast, the solution in [6] involves Padé approximation, which can improve the region of convergence.
Table 4. A numerical comparison of the approximate solution to Example 5 when k = 10 for different values of x in [0,1].
xi Reference [5] Reference [6] Reference [7] Reference [8] Present method
0 0 0 0 0 0
0.1 0.0016 0.0166 0.0016 0.0027 0.0017
0.2 0.0065 0.0333 0.0066 0.0038 0.0067
0.3 0.0145 0.0500 0.0149 0.0152 0.0149
0.4 0.0253 0.0666 0.0266 0.0341 0.0265
0.5 0.0385 0.0833 0.0416 0.0456 0.0412
0.6 0.0536 0.1000 0.0598 0.0601 0.0589
0.7 0.0700 0.1166 0.0813 0.0935 0.0797
0.8 0.0870 0.1333 0.1060 0.1399 0.1034
0.9 0.1038 0.1500 0.1338 0.1786 0.1298
1 0.1199 0.1666 0.1646 0.2005 0.1588

In the next example, we show that the RPS method is capable of reproducing the exact solution to a new version of the Lane-Emden equation. Furthermore, we show that the consecutive error is a useful indicator in the iteration progresses, and moreover, this error can be used to study the structural analysis of the RPS method.

4.6. Example  6

Consider the following nonlinear nonhomogeneous singular initial-value problem:
()
which is subject to the initial conditions
()
where f(x) is chosen so that the exact solution is y(x) = sin(x − 1) + cos (x − 1).
If we select the initial guess approximation as y2(x) = x − (1/2)(x − 1) 2, then the 10th-truncated series of the RPS solution for (46) and (47) will be
()
Furthermore, if we separate the above approximation’s odd and even terms, then it is easy to discover that the exact solution of (46) and (47) has the general form that coincides with the exact solution
()
Thus, the approximate solution of (46) and (47) has the general form that coincides with the exact solution
()

Remark. While one cannot know the exact error without knowing the solution, in most cases the consecutive error can be used as a reliable indicator in the iteration progresses. In Table 5, the values of the consecutive error functions , i = 1,2, 3  for two consecutive approximate solutions have been calculated for various values of x in  [0,1]  with a step size of 0.1; the goal was to measure the difference between the consecutive solutions that were obtained from the 10th-order RPS solutions for (46) and (47). However, the computational results provide a numerical estimate for the convergence of the RPS method. Indeed, it is clear that the accuracy that is obtained using the present method is advanced by using an approximation with only a few additional terms. In addition, we can conclude that higher accuracy can be achieved by evaluating more components of the solution. Thus, we terminate the iteration in our method.

Table 5. The values of the consecutive error function Conk(x) to Example 6 when k = 10,15,20,25 for different values of x in [1,3].
  xi Con10(xi) Con15(xi) Con20(xi) Con25(xi)
1 0 0 0 0
1.2 5.130672 × 10−16 3.132278 × 10−25 4.104743 × 10−35 1.664029 × 10−45
1.4 1.050762 × 10−12 2.052770 × 10−20 8.608271 × 10−29 1.116711 × 10−37
1.6 9.088831 × 10−11 1.348343 × 10−17 4.293706 × 10−25 4.229738 × 10−33
1.8 2.151960 × 10−9 1.345303 × 10−15 1.805285 × 10−22 7.494120 × 10−30
2 2.505211 × 10−8 4.779477 × 10−14 1.957294 × 10−20 2.479596 × 10−27
2.2 1.861393 × 10−7 8.836501 × 10−13 9.004555 × 10−19 2.838529 × 10−25
2.4 1.014501 × 10−6 1.040948 × 10−11 2.292687 × 10−17 1.562104 × 10−23
2.6 4.407214 × 10−6 8.816580 × 10−11 3.785957 × 10−16 5.029219 × 10−22
2.8 1.610059 × 10−5 5.804175 × 10−10 4.491369 × 10−15 1.075143 × 10−20
3 5.130672 × 10−5 3.132278 × 10−9 4.104743 × 10−14 1.664029 × 10−19

5. Conclusion

The goal of the present work was to develop an efficient and accurate method to solve the Lane-Emden-type equations of singular initial-value problems. We can conclude that the RPS method is a powerful and efficient technique that finds an approximate solution to linear and nonlinear Lane-Emden equations. The proposed algorithm produced a rapidly convergent series with easily computable components using symbolic computation software. The results obtained by the RPS method are very effective and convenient in linear and nonlinear cases because they require less computational work and time. This convenient feature confirms our belief that the efficiency of our technique will give it much greater applicability in the future for general classes of linear and nonlinear singular problems.

Acknowledgments

This work was completed during the visit of the author A. Sami Bataineh (ASB) to the Universiti Kebangsaan Malaysia (UKM), in June–August 2013, as a visiting researcher of mathematics. The authors I. Hashim and A. S. Bataineh gratefully acknowledge the Grant provided by UKM out of the University Research Fund DIP-2012-12.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.