Volume 2013, Issue 1 359265

Research Article

Open Access

Neural Network Based Finite-Time Stabilization for Discrete-Time Markov Jump Nonlinear Systems with Time Delays

Fei Chen

orcid.org/0000-0002-4028-1922

Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Fei Liu,

Corresponding Author

Fei Liu

[email protected]

Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Hamid Reza Karimi,

Hamid Reza Karimi

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

Fei Chen,

Fei Chen

orcid.org/0000-0002-4028-1922

Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Fei Liu,

Corresponding Author

Fei Liu

[email protected]

Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China jiangnan.edu.cn

Search for more papers by this author

Hamid Reza Karimi,

Hamid Reza Karimi

Department of Engineering, Faculty of Engineering and Science, University of Agder, 4898 Grimstad, Norway uia.no

Search for more papers by this author

First published: 30 September 2013

https://doi.org/10.1155/2013/359265

Academic Editor: Lixian Zhang

Share a link

Email
Wechat
Bluesky

Abstract

This paper deals with the finite-time stabilization problem for discrete-time Markov jump nonlinear systems with time delays and norm-bounded exogenous disturbance. The nonlinearities in different jump modes are parameterized by neural networks. Subsequently, a linear difference inclusion state space representation for a class of neural networks is established. Based on this, sufficient conditions are derived in terms of linear matrix inequalities to guarantee stochastic finite-time boundedness and stochastic finite-time stabilization of the closed-loop system. A numerical example is illustrated to verify the efficiency of the proposed technique.

1. Introduction

Markov jump systems (MJSs) are an important class of stochastic dynamic systems, which are popular when modeling an abrupt change in the system structure and parameters, such as component failures or repairs, changing subsystem interconnections and environmental disturbance. This family of systems has great practical potential in a variety of fields, such as solar thermal central receivers systems, economic systems, communication systems, manufacturing systems, and networked control systems [1–4]. MJSs have been extensively studied since the pioneering work on quadratic control of MJSs [5], and many achievements have been made on Lyapunov stochastic stability and stabilization in the last three decades [6–18].

However, it is worth noting that the Lyapunov stochastically stable systems may not possess good or expected transient characteristics over a finite-time horizon. In many practical problems, it is of interest to investigate the stability of a system over a finite interval of time. For example, referring to aircraft control, it requests that, during the execution of a certain task, the state variables should not exceed some threshold under all admissible pilot inputs and in the presence of wind disturbances. Classical control theory does not directly address this requirement, because it focuses mainly on the asymptotic behavior of the system (over an infinite-time interval) and does not usually specify bounds on the trajectories. Therefore, it is necessary to limit the state in an acceptable region and consider finite-time stability (FTS) given by Dorato [19].

The concept of FTS has been further extended into finite-time boundness (FTB) [20, 21], when system possesses bounded exogenous disturbance. A linear matrix inequality (LMI) framework has been established to distinguish FTS and Lyapunov asymptotical stability [22–24]. Compared with Lyapunov stochastically stable condition, FTS relaxes the condition by allowing that the Lyapunov-like function can increase at every sampling time instant. That is why FTS is so attractive and widely used in practical engineering.

As MJSs are considered, a number of results on stochastic FTS or stochastic FTB have been developed [25–28], and recently, the obtained results have been extended to continuous-time MJSs with nonlinearities via fuzzy or neural network approach [24, 29, 30]. In order to make the stochastic systems more manageable and satisfy the requirements for finite-time behavior of a system in engineering fields, it motivates us to investigate the finite-time stability and stabilization problems for a class of MJSs. Furthermore, time delay is a common phenomenon and is inevitable in practice systems [31–33]. Due to the interaction among system dynamics, stochastic jumps, and time delays, the dynamics of MJSs with time delay become more complex than MJSs without time delay and time delay systems without jumps. So far, in comparison with the literatures available for continuous-time nonlinear MJSs with time delays, the corresponding FTS or FTB results for discrete-time nonlinear systems have been relatively few.

It is, therefore, the main purpose of this paper to shorten such a gap by investigating the finite-time stabilization problem for discrete-time nonlinear MJSs with time delays. With neural networks, the nonlinearities of MJSs are approximated firstly by linear difference inclusion under state-space representation. Then, a mode-dependent finite-time controller is developed to make the nonlinear MJSs stochastic finite-time stabilizable for all admissible approximation errors of the neural networks and the norm-bounded external disturbances. The controller gains could be derived by solving a set of LMIs. An attractive feature of the proposed scheme is that the coupling relationship between time delay and given finite-time horizon is explored by obtaining delay-independent conditions.

Notations in this paper are fairly standard. Rⁿ and R^n×m denote n-dimensional Euclidean space and the set of all the n × m real matrices, respectively; A^T (or x^T) and A⁻¹ denote the transpose of the matrix A (or the vector x) and the inverse of the matrix A, respectively. λ_max(A) and λ_min(A) denote, respectively, the maximal and minimal eigenvalues of a real matrix A, ∥A∥ denotes the Euclidean norm of matrix A, E{·} denotes the mathematics statistical expectation of the stochastic process or vector, l₂[0 N) is the space of summable infinite sequence over [0 N), P > 0 stands for a positive-definite matrix, I is the unit matrix with appropriate dimensions, and “*” means the symmetric terms in a symmetric matrix.

2. System Description and Problem Formulation

We consider a nonlinear discrete-time MJS, which can be described by the following mathematical model:

()

where x_k ∈ Rⁿ is the vector of state variables, u_k ∈ R^m is the controlled input, f(·) is a discrete nonlinear mapping with f(0) = 0 but not assumed to be known a prior, and

is the exogenous disturbances satisfying

()

For each possible value of r_k = i, we denote

()

where r_k is a discrete-state Markov chain taking values in M = {1,2, …, s} with transition probabilities

()

where π_ij is the transition probabilities from mode i to mode j that satisfies

()

For each mode i, nonlinear function f_i(x_k) is to be parameterized by neural networks. Such parameterization makes sense because any nonlinear function can be approximated arbitrarily well on a compact interval by a neural network. Let the L-layered perceptrons N_i(x_k, W_r1, W_r2, …, W_rL) be suitably trained to approximate the nonlinear term f_i(x_k), which is described in matrix-vector notation as

()

where all the weight matrices

, r = 1, …, L, from the (r − 1)th layer to the (r − L)th layer will be determined via back propagation (BP) procedure [24]; the activation function vector of rth layer is defined as

, where n_r indicates the neurons of rth layer and let

()

The maximum and minimum derivatives of activation function ϕ_il are defined as follows:

()

For rth layer of neural network, activation function ϕ_il can be rewritten as the following min-max form:

()

where h_il(m), m = 0,1, are a set of positive real numbers associated with ϕ_il satisfying h_il(m) > 0 and h_il(0) + h_il(1) = 1.

According to the approximation theorem, for given accuracy ρ_i > 0, there exist ideal constant weight matrices

defined as

()

where D is a compact set D ∈ R^m, such that

()

For each mode i, denote a set of n_r dimensional index vectors of the rth layer as

()

where σ_i is used as a binary indicator. Obviously, the rth layer with n_r neurons has

combinations of binary indicator with m = 0,1, and the elements of index vectors for all L layers neural network have

combinations in the set

()

By using (8) and adopting the compact representation [34], the multilayer neural network (6) can be expressed as follows:

()

where

()

Thus by means of multilayer neural network, the nonlinear MJS (1) is translated into a group of LDIs with error bounds, in which the different inclusion is powered by stochastic Markov process; that is,

()

where

()

denotes the approximation errors of networks.

Remark 1. The detailed structure and quantitative size of error dynamics Δf_i(x_k) are not needed, but only norm-bounded assumption is required. This condition is easily satisfied in practical cases, such as bioinformatics system, medical diagnosis, fault diagnosis, and image and pattern recognition. Actually, the approximation error between the target function and the closest neural network function of a given network family can be made as small as desired by increasing the number of nodes [35]. Also the bounds of norm may vary according to different nonlinearities in different modes.

3. Main Results

Based on the LDI model (16) of networks, we consider the following discrete-time state feedback control law for nonlinear stochastic MJS (1):

()

The resulting closed-loop system can be obtained as follows:

()

where

()

The aim of this paper is to find some sufficient conditions which guarantee stochastic finite-time boundness and stochastic finite-time stabilization of the closed-loop system (19). The general idea of finite-time control can be formalized through the following definitions over a finite-time interval for some given initial conditions.

Definition 2 (stochastic finite-time stability). A discrete-time nonlinear MJS (1) (setting u_k = 0 and w_k = 0) is said to be, stochastic finite-time stability (FTS) with respect to given (c₁, c₂, G, N), where c₂ > c₁ and G > 0, if , k ∈ {1,2, …, N} whenever .

Definition 3 (stochastic finite-time boundness). A discrete-time nonlinear MJS (1) (setting u_k = 0) is said to be of stochastic finite-time boundness (FTB) with respect to (c₁, c₂, G, N, δ) with c₂ > c₁ and G > 0, if , whenever .

Before proceeding further, we introduce the following lemmas which will be needed for the derivation of our main results.

Lemma 4. The closed-loop system (19) is stochastic FTB with respect to the given (c₁, c₂, G, N, δ) and scalar α ≥ 0, if there exist mode-dependent symmetric positive-definite matrix P_i and symmetric positive-definite matrices Q and S such that

()

where

, and λ_max(·), λ_min(·) indicate the maximal and minimal eigenvalues of the augment, respectively.

Proof. For the closed-loop system (19), choose a stochastic Lyapunov function candidate as

()

Simple calculation shows that

()

where

()

Conditions (21) and (24) imply that

()

Noting that α ≥ 0, we can obtain from (26) that

()

Note that

()

According to (27)-(28), one has

()

Condition (19) implies that, for k ∈ {1,2, …, N}, . This completes the proof.

Now, we direct our attention to present a solution to the problem of finite-time stabilizing controller design. Such controller is provided by the following theorem.

Theorem 5. The closed-loop system (19) is stochastic finite-time stabilizable via state feedback with respect to the given (c₁, c₂, G, N, δ) and scalar α ≥ 0, if there exist matrices , Y_i, H = H^T > 0, S = S^T > 0, and R = R^T > 0 and scalars λ₁, λ₂, λ₃, λ₄ > 0 such that

()

Proof. By using Schur complement, from condition (21) in Lemma 4, it follows that

()

where

()

Performing matrix elementary transformation to the above inequality, we have

()

Performing a congruence to the above condition by

, using Schur complement, and letting

and Y_i = K_iX_i, we get

()

where

()

By using Schur complement to (36) and letting

, we obtain the linear matrix inequality (30) in Theorem 5.

On the other hand, we consider

()

Condition (22) follows that

()

It is easy to check that the above inequality is guaranteed by imposing the following conditions

()

which are equivalent to conditions (31)-(32). This completes the proof.

Remark 6. It is worth pointing out that Theorem 5 is not a delay-dependent sufficient criterion, which is conservative when the delay is small. Delay-dependent result can be developed in the same way by choosing a Lyapunov functional that includes more entries, as was done in [36], or delay fractioning approach that can be employed as was done in [31–33].

Remark 7. The coupling relationship between time delay and given finite-time horizon of the underlying system is obtained through a finite-time stable constraint (32) in Theorem 5. From condition (32), it can be seen that, in given finite-time horizon, if the time delay d is larger, constraint (32) is more difficult to be satisfied, which means that the existence of time delay increases the instability of system.

4. Numerical Example

Consider discrete-time Markov jump nonlinear system (1) with three operation modes and the following data:

()

Now, a single hidden layer neural network with 2 hidden neurons was chosen to approximate the nonlinear functions f_i(x_k). All parameters of activation functions associated with the hidden layer were chosen to be q_il = 0.5 and λ_il = 1. For these activation functions, we have s_il(0, ϕ_il) = 0 and s_il(1, ϕ_il) = 1. The connection weights are trained offline by using BP algorithm. The initial weights and state vector are placed by uniformly distributed random numbers in [−1 1]. After 1000 training steps, the optimal approximation weights are as follows:

()

The upper bound of approximation error is estimated as ρ_i = 0.022. Obviously, in this case, we have Θ = 2² × 2¹. According to (15),

can be obtained as follows:

()

The initial state and initial mode are taken as

and r₀ = 1, respectively. The iterative step is taken as N = 7. The mode path from time step 0 to time step 7 is generated randomly and it is shown in Figure 1. Let c₁ = 0.5, c₂ = 2, N = 7, G = I, d = 0.5, α = 0.5, and δ² = 1. By solving the matrix inequalities in Theorem 5, we have the following controller gains:

()

The state trajectories of the free and controlled MJLS (16) are drawn in Figures 2 and 3, respectively. It could be seen that the free MJLS (16) is not stochastic FTB because the trajectory exceeds the given bound

. However, the trajectory is limited between the two ellipsoids regions by employing the proposed control move which satisfactorily justify that the closed-loop MJLS (16) is stochastic FTB.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Jump modes.

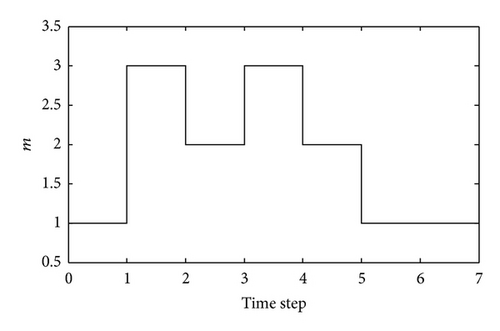
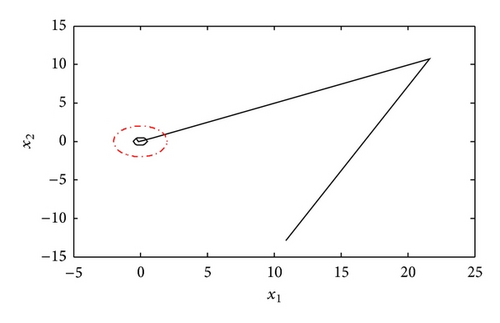
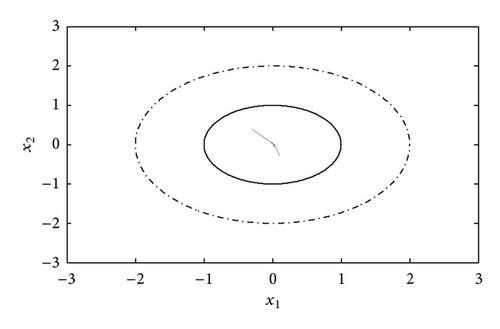
It should be pointed out that, in the simulation example, as long as the choice of initial condition is satisfied with , then the system is robustly finite-time stabilizable; that is, system trajectories stay within a given bound.

5. Conclusions

The finite-time stabilization problem for discrete-time Markovian jump nonlinear system with time delay and norm-bounded exogenous disturbance is investigated in this paper. The nonlinearities are parameterized by multilayer neural network and the relationship between time delay and given finite-time horizon is explored with delay-independent conditions. The proposed framework is versatile and can accommodate a number of challenging design problems including finite-time control and filtering of discrete-time or continuous-time nonlinear MJS with parameter uncertainties, time delays, and so on. The future work can consider some delay-dependent approaches or delay fractioning approaches to reduce the conservativeness introduced by time delay.

Acknowledgments

This work was partially supported by the National Natural Science Foundation of China (Grant no. 61104121) and the 111 Project (Grant no. B12018), and the third author would also like to thank the Alexander-von-Humboldt Foundation for providing the support to this research.

References

1 BlairW. P.Jr. and Sworder D. D., Feedback control of a class of linear discrete systems with jump parameters and quadratic cost criteria, International Journal of Control. (1975) 21, 833–841, MR0401310, https://doi.org/10.1080/00207177508922037, ZBL0326.93036.
10.1080/00207177508922037
Web of Science® Google Scholar
2 Sworder D. D. and Rogers R. O., An LQG solution to a control problem with solar thermal receiver, IEEE Transactions on Automatic Control. (1983) 28, no. 10, 971–978, 2-s2.0-0020829468.
10.1109/TAC.1983.1103151
Web of Science® Google Scholar
3 Athans M., Command and control theory: a challenge to control science, IEEE Transactions on Automatic Control. (1987) 32, no. 4, 286–293, 2-s2.0-0023324578.
10.1109/TAC.1987.1104607
Web of Science® Google Scholar
4 Assawinchaichote W., Nguang S. K., and Shi P., Robust H_∞ fuzzy filter design for uncertain nonlinear singularly perturbed systems with Markovian jumps: an LMI approach, Information Sciences. (2007) 177, no. 7, 1699–1714, https://doi.org/10.1016/j.ins.2006.10.006, MR2303181, ZBL1113.93078.
10.1016/j.ins.2006.10.006
Web of Science® Google Scholar
5 Krasovskii N. M. and Lidskii E. A., Analytical design of controllers in systems with random attributes, Automation and Remote Control. (1961) 22, no. 1–3, 1021–1025, 1141–1146, 1289–1294.
Google Scholar
6 Ji Y. and Chizeck H. J., Controllability, stabilizability, and continuous-time Markovian jump linear quadratic control, IEEE Transactions on Automatic Control. (1990) 35, no. 7, 777–788, https://doi.org/10.1109/9.57016, MR1058362, ZBL0714.93060.
10.1109/9.57016
Web of Science® Google Scholar
7 Shi P., Xia Y., Liu G. P., and Rees D., On designing of sliding-mode control for stochastic jump systems, IEEE Transactions on Automatic Control. (2006) 51, no. 1, 97–103, https://doi.org/10.1109/TAC.2005.861716, MR2192795.
10.1109/TAC.2005.861716
Web of Science® Google Scholar
8 Mahmoud M. S., Shi P., Boukas E. K., and Jain L., Simultaneous H₂/H_∞ control of uncertain jump systems with functional time-delays, International Journal of Robust and Nonlinear Control. (2008) 18, no. 3, 296–318, https://doi.org/10.1002/rnc.1221, MR2378403.
10.1002/rnc.1221
Web of Science® Google Scholar
9 Luan X., Liu F., and Shi P., Neural network based stochastic optimal control for nonlinear Markov jump systems, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 8, 3715–3723, 2-s2.0-77956238294.
Web of Science® Google Scholar
10 Liu J., Gu Z., and Hu S., H_∞ filtering for Markovian jump systems with time-varying delays, International Journal of Innovative Computing, Information and Control. (2011) 7, no. 3, 1299–1310, 2-s2.0-79951704915.
Web of Science® Google Scholar
11 Hu Y., Lam J., and Liang J., Consensus control of multi-agent systems with missing data in actuators and Markovian communication failure, International Journal of Systems Science. (2013) 44, no. 10, 1867–1878.
10.1080/00207721.2012.670298
Web of Science® Google Scholar
12 He X., Wang Z., and Zhou D. H., Robust fault detection for networked systems with communication delay and data missing, Automatica. (2009) 45, no. 11, 2634–2639, https://doi.org/10.1016/j.automatica.2009.07.020, MR2889323, ZBL1180.93101.
10.1016/j.automatica.2009.07.020
Web of Science® Google Scholar
13 Zhang L. and Boukas E.-K., Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities, Automatica. (2009) 45, no. 2, 463–468, https://doi.org/10.1016/j.automatica.2008.08.010, MR2527344, ZBL1158.93414.
10.1016/j.automatica.2008.08.010
Web of Science® Google Scholar
14 Shen M. Q. and Yang G. H., Nonfragile H_∞ filtering of continuous Markov jump linear systems with general transition probabilities, Journal of Dynamic Systems, Measurement, and Control. (2013) 135, no. 3, 031005.
10.1115/1.4023403
Web of Science® Google Scholar
15 Shen M. and Ye D., Improved fuzzy control design for nonlinear Markovian-jump systems with incomplete transition descriptions, Fuzzy Sets and Systems. (2013) 217, 80–95, https://doi.org/10.1016/j.fss.2012.11.014, MR3021666.
10.1016/j.fss.2012.11.014
Web of Science® Google Scholar
16 Zhang L. X. and Lam J., Necessary and sufficient conditions for analysis and synthesis of Markov jump linear systems with incomplete transition descriptions, IEEE Transactions on Automatic Control. (2010) 55, no. 7, 1695–1701, https://doi.org/10.1109/TAC.2010.2046607, MR2675834.
10.1109/TAC.2010.2046607
Web of Science® Google Scholar
17 Zhang L. X., Boukas E.-K., and Lam J., Analysis and synthesis of Markov jump linear systems with time-varying delays and partially known transition probabilities, IEEE Transactions on Automatic Control. (2008) 53, no. 10, 2458–2464, https://doi.org/10.1109/TAC.2008.2007867, MR2466607.
10.1109/TAC.2008.2007867
Web of Science® Google Scholar
18 Zhang L. X. and Boukas E.-K., Mode-dependent H_∞ filtering for discrete-time Markovian jump linear systems with partly unknown transition probabilities, Automatica. (2009) 45, no. 6, 1462–1467, https://doi.org/10.1016/j.automatica.2009.02.002, MR2879450, ZBL1166.93378.
10.1016/j.automatica.2009.02.002
Web of Science® Google Scholar
19 Dorato P., Short time stability in linear time-varying systems, Proceedings of the of the IRE international Convention Record, Part 4, 1961, New York, NY, USA, 83–87.
Google Scholar
20 Amato F., Ariola M., and Dorato P., Finite-time control of linear systems subject to parametric uncertainties and disturbances, Automatica. (2001) 37, no. 9, 1459–1463, 2-s2.0-0035452456, https://doi.org/10.1016/S0005-1098(01)00087-5, ZBL0983.93060.
10.1016/S0005-1098(01)00087-5
Web of Science® Google Scholar
21 Amato F. and Ariola M., Finite-time control of discrete-time linear systems, IEEE Transactions on Automatic Control. (2005) 50, no. 5, 724–729, https://doi.org/10.1109/TAC.2005.847042, MR2141582.
10.1109/TAC.2005.847042
Web of Science® Google Scholar
22 Moulay E., Dambrine M., Yeganefar N., and Perruquetti W., Finite-time stability and stabilization of time-delay systems, Systems & Control Letters. (2008) 57, no. 7, 561–566, https://doi.org/10.1016/j.sysconle.2007.12.002, MR2415969, ZBL1140.93447.
10.1016/j.sysconle.2007.12.002
Web of Science® Google Scholar
23 Luan X. L., Liu F., and Shi P., Robust finite-time H_∞ control for nonlinear jump systems via neural networks, Circuits, Systems, and Signal Processing. (2010) 29, no. 3, 481–498, https://doi.org/10.1007/s00034-010-9158-8, MR2610409, ZBL1191.93028.
10.1007/s00034-010-9158-8
Web of Science® Google Scholar
24 Zhang X. F., Feng G., and Sun Y. H., Finite-time stabilization by state feedback control for a class of time-varying nonlinear systems, Automatica. (2012) 48, no. 3, 499–504, https://doi.org/10.1016/j.automatica.2011.07.014, MR2889447, ZBL1244.93142.
10.1016/j.automatica.2011.07.014
Web of Science® Google Scholar
25 Amato F., Ambrosino R., Ariola M., and Cosentino C., Finite-time stability of linear time-varying systems with jumps, Automatica. (2009) 45, no. 5, 1354–1358, https://doi.org/10.1016/j.automatica.2008.12.016, MR2531617, ZBL1162.93375.
10.1016/j.automatica.2008.12.016
Web of Science® Google Scholar
26 Hou L. L., Zong G. D., and Wu Y. Q., Finite-time control for switched delay systems via dynamic Output feedback, International Journal of Innovative Computing, Information and Control. (2012) 8, no. 7, 4901–4913.
Web of Science® Google Scholar
27 Zhang W. H. and An X. Y., Finite-time control of linear stochastic systems, International Journal of Innovative Computing, Information and Control. (2008) 4, no. 3, 689–696, 2-s2.0-63649087412.
Web of Science® Google Scholar
28 Luan X.-L., Liu F., and Shi P., Finite-time stabilization of stochastic systems with partially known transition probabilities, Journal of Dynamic Systems, Measurement and Control. (2011) 133, no. 1, 2-s2.0-78650730762, https://doi.org/10.1115/1.4002716, 014504.
10.1115/1.4002716
Web of Science® Google Scholar
29 Yang D. and Cai K.-Y., Finite-time quantized guaranteed cost fuzzy control for continuous-time nonlinear systems, Expert Systems with Applications. (2010) 37, no. 10, 6963–6967, 2-s2.0-80053061477, https://doi.org/10.1016/j.eswa.2010.03.024.
10.1016/j.eswa.2010.03.024
Web of Science® Google Scholar
30 Luan X., Liu F., and Shi P., Neural-network-based finite-time H_∞ control for extended Markov jump nonlinear systems, International Journal of Adaptive Control and Signal Processing. (2010) 24, no. 7, 554–567, MR2680719, ZBL1200.93125.
10.1002/acs.1143
Web of Science® Google Scholar
31 Hu J., Wang Z., Gao H., and Stergioulas L. K., Robust sliding mode control for discrete stochastic systems with mixed time delays, randomly occurring uncertainties, and randomly occurring nonlinearities, IEEE Transactions on Industrial Electronics. (2012) 59, no. 7, 3008–3015, 2-s2.0-84857382236, https://doi.org/10.1109/TIE.2011.2168791.
10.1109/TIE.2011.2168791
Web of Science® Google Scholar
32 Hu J., Wang Z. D., and Gao H. J., A delay fractioning approach to robust sliding mode control for discrete-time stochastic systems with randomly occurring non-linearities, IMA Journal of Mathematical Control and Information. (2011) 28, no. 3, 345–363, https://doi.org/10.1093/imamci/dnr008, MR2837649, ZBL1228.93025.
10.1093/imamci/dnr008
PubMed Web of Science® Google Scholar
33 Hu J., Wang Z. D., Niu Y. G., and Stergioulas L. K., H_∞ sliding mode observer design for a class of nonlinear discrete time-delay systems: a delay-fractioning approach, International Journal of Robust and Nonlinear Control. (2012) 22, no. 16, 1806–1826, https://doi.org/10.1002/rnc.1785, MR2983311.
10.1002/rnc.1785
Web of Science® Google Scholar
34 Limanond S. and Si J., Neural-network-based control design: an LMI approach, IEEE Transactions on Neural Networks. (1998) 9, no. 6, 1422–1429, 2-s2.0-0032207886, https://doi.org/10.1109/72.728392.
10.1109/72.728392
CAS PubMed Web of Science® Google Scholar
35 Barron A. R., Approximation and estimation bounds for artificial neural networks, Machine Learning. (1994) 14, no. 1, 115–133, 2-s2.0-0001325515, https://doi.org/10.1007/BF00993164, ZBL0818.68127.
10.1007/BF00993164
Web of Science® Google Scholar
36 Zhang L., Boukas E.-K., and Haidar A., Delay-range-dependent control synthesis for time-delay systems with actuator saturation, Automatica. (2008) 44, no. 10, 2691–2695, https://doi.org/10.1016/j.automatica.2008.03.009, MR2531070, ZBL1155.93350.
10.1016/j.automatica.2008.03.009
Web of Science® Google Scholar

All articles

Neural Network Based Finite-Time Stabilization for Discrete-Time Markov Jump Nonlinear Systems with Time Delays

Abstract

1. Introduction

2. System Description and Problem Formulation

3. Main Results

4. Numerical Example

5. Conclusions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Neural Network Based Finite-Time Stabilization for Discrete-Time Markov Jump Nonlinear Systems with Time Delays

Abstract

1. Introduction

2. System Description and Problem Formulation

3. Main Results

4. Numerical Example

5. Conclusions

Acknowledgments

References

Figures

References

Related

Information