Abstract and Applied Analysis
Volume 2013, Issue 1 316978
Research Article
Open Access

Mappings for Special Functions on Cantor Sets and Special Integral Transforms via Local Fractional Operators

Yang Zhao, 

Yang Zhao

Electronic and Information Technology Department, Jiangmen Polytechnic, Jiangmen 529090, China

College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130061, China jlu.edu.cn

Search for more papers by this author
Dumitru Baleanu, 

Dumitru Baleanu

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, P.O. Box 80204, Jeddah 21589, Saudi Arabia kau.edu.sa

Department of Mathematics and Computer Sciences, Faculty of Arts and Sciences, Cankaya University, 06530 Ankara, Turkey cankaya.edu.tr

Institute of Space Sciences, Magurele, 077125 Bucharest, Romania spacescience.ro

Search for more papers by this author
Mihaela Cristina Baleanu, 

Mihaela Cristina Baleanu

Mihail Sadoveanu Theoretical High School, District 2, Street Popa Lazar No. 8, 021586 Bucharest, Romania

Search for more papers by this author
De-Fu Cheng, 

Corresponding Author

De-Fu Cheng

College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130061, China jlu.edu.cn

Search for more papers by this author
Xiao-Jun Yang, 

Xiao-Jun Yang

Department of Mathematics and Mechanics, China University of Mining and Technology, Xuzhou Campus, Xuzhou, Jiangsu 221008, China

Search for more papers by this author
First published: 30 October 2013
https://doi.org/10.1155/2013/316978
Citations: 4
Academic Editor: Ali H. Bhrawy

Abstract

The mappings for some special functions on Cantor sets are investigated. Meanwhile, we apply the local fractional Fourier series, Fourier transforms, and Laplace transforms to solve three local fractional differential equations, and the corresponding nondifferentiable solutions were presented.

1. Introduction

Special functions [1] play an important role in mathematical analysis, function analysis physics, and so on. We recall here some very well examples, the Gamma function [2], hypergeometric function [3], Bessel functions [4], Whittaker function [5], G-function [6], q-special functions [7], Fox’s H-functions [8], Mittag-Leffler function [9], and Wright’s function [10].

The Mittag-Leffler function had successfully been applied to solve the practical problems [11–15]. For example, the Mittag-Leffler-type functions in fractional evolution processes were suggested [15]. Solutions for fractional reaction-diffusion equations via Mittag-Leffler-type functions were discussed [16]. The Mittag-Leffler stability of fractional order nonlinear dynamic systems was presented [17]. Models based on Mittag-Leffler functions for anomalous relaxation in dielectrics were proposed [18]. In [19], the anomalous relaxation via the Mittag-Leffler functions was reported. The continuous-time finance based on the Mittag-Leffler function was given [20]. In [21], the fractional radial diffusion in a cylinder based on the Mittag-Leffler function was investigated. In [22], the Mittag-Leffler stability theorem for fractional nonlinear systems with delay was considered. The stochastic linear Volterra equations of convolution type based on the Mittag-Leffler function were suggested in [23].

Recently, based on the Mittag-Leffler functions on Cantor sets via the fractal measure, the special integral transforms based on the local fractional calculus theory were suggested in [24]. In this work, some applications for the local fractional calculus theory are studied in [24–36]. The main aim of this paper is to investigate the mappings for special functions on Cantor sets and some applications of special integral transforms to nondifferentiable problems.

The paper is organized as follows. In Section 2, the mappings for special functions on Cantor sets are investigated. In Section 3, the special integral transforms within local fractional calculus and some applications to nondifferentiable problems are presented. Finally, in Section 4, the conclusions are presented.

2. Mappings for Special Functions on Cantor Sets

In order to give the mappings for special functions on Cantor sets, we first recall some basic definitions about the fractal measure theory [25].

Let Lebesgue-Cantor staircase function be defined as [25]
()
where F is a cantor set, Hα(·) is the α-dimensional Hausdorff measure, is local fractional integral operator [24–31], and Γ(·) is a Gamma function.
Following (1), we obtain
()
which is a Lebesgue-Cantor staircase function. For its graph, please see [28].

In this way, we define some real-valued functions on Cantor sets as follows [24–26].

The Cantor staircase function is defined as [25]
()
and its graph is shown in Figure 1.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Graph of x2α for α = ln 2/ln 3.
The Mittag-Leffler functions on Cantor sets are given by [24, 25]
()
and we draw the corresponding graph in Figure 2.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Graph of Eα(xα) for α = ln 2/ln 3.
The sine on Cantor sets is defined by [24, 25]
()
and its corresponding graph is depicted in Figure 3.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Graph of sinαxα for α = ln 2/ln 3.
The cosine on Cantor sets is [24, 25]
()
with graph in Figure 4.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Graph of cos αxα for α = ln 2/ln 3.
Hyperbolic sine on Cantor sets is defined by [24, 25]
()
and we draw its graphs as shown in Figure 5.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Graph of sinh αxα for α = ln 2/ln 3.
Hyperbolic cosine on Cantor sets is defined as [24, 25]
()
and its graph is shown in Figure 6.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Graph of cosh αxα for α = ln 2/ln 3.
Following (4)–(8), we have
()
where iα is a fractal unit of an imaginary number [24, 26–32].
If for ε, δ > 0 and ε, δ ∈ R, f(x) satisfies the condition [24–26]
()
for x ∈ [a, b] we write it as follows:
()

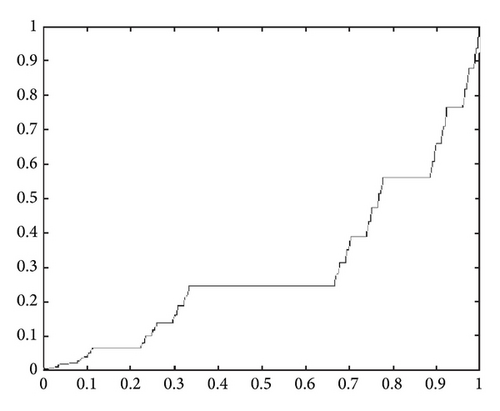
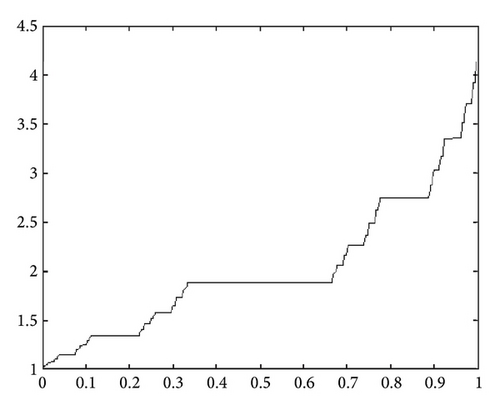
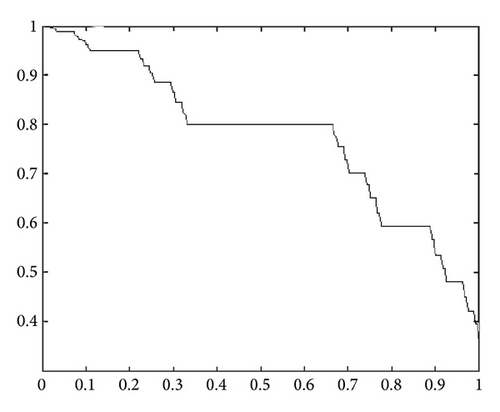
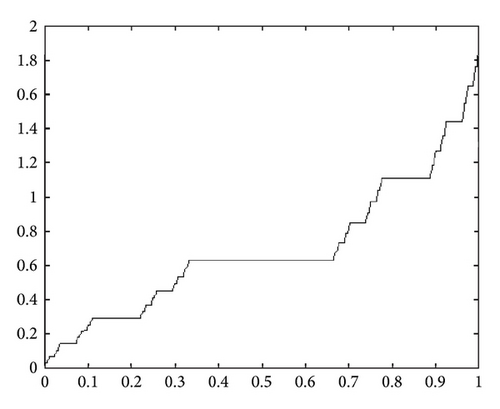
3. Special Integral Transforms within Local Fractional Calculus

In this section, we introduce the conceptions of special integral transforms within the local fractional calculus concluding the local fractional Fourier series and Fourier and Laplace transforms. After that, we present three illustrative examples.

3.1. Definitions of Special Integral Transforms within Local Fractional Calculus

We here present briefly some results used in the rest of the paper.

Let f(x) ∈ Cα(−∞, ∞). Local fractional trigonometric Fourier series of f(x) is given by [24, 26–28]
()
The local fractional Fourier coefficients read as
()
We notice that the above results are obtained from Pythagorean theorem in the generalized Hilbert space [24, 26–28].
Let f(x) ∈ Cα(−∞, ∞). The local fractional Fourier transform of f(x) is suggested by [24, 29–32]
()
The inverse formula is expressed as follows [24, 29–32]:
()
Let f(x) ∈ Cα(−∞, ∞). The local fractional Laplace transform of f(x) is defined as [24, 32, 33]
()
The inverse formula local fractional Laplace transform of f(x) is derived as [24, 32, 33]
()
where f(x) is local fractional continuous, sα = βα + iα∞α, and Re(s) = β > 0.

For more details of special integral transforms via local fractional calculus, see [24, 32, 33] and the references therein.

3.2. Applications of Local Fractional Fourier Series and Fourier and Laplace Transforms to the Differential Equation on Cantor Sets

We now present the powerful tool of the methods presented above in three illustrative examples.

Example 1. Let us begin with the local fractional differential equation on Cantor set in the following form:

()
where a and b are constants and the nondifferentiable function f(x) is periodic of period 2π so that it can be expanded in a local fractional Fourier series as follows:
()
Here, we give a particular solution in the following form:
()

Following (20), we have

()
Submitting (20)-(21) into (18), we obtain
()
Hence, we get
()
Therefore, we can calculate
()
In view of (24), we give the solution of (18) as follows:
()

Example 2. We now consider the following differential equation on Cantor sets:

()
subject to the initial value condition
()
where p is constant and f(t) is the local fractional continuous function so that its local fractional Fourier transform exists.

Application of local fractional Fourier transform gives

()
so that
()
From (29), we have
()
Therefore, taking the inverse formula of local fractional Fourier transform, we have
()

Example 3. Let us find the solution to the differential equation on Cantor sets

()
subject to the initial value condition
()
where f(t) is the local fractional continuous function so that its local fractional Laplace transform exists.

Taking the local fractional Laplace transform, from (32), we have

()
so that
()
When the local fractional convolution of two functions is given by [24]
()
and the local fractional Laplace transform of f1(t)*f2(t) is [24]
()
the inverse formula of the local fractional Laplace transform together with the local fractional convolution theorem gives the solution
()

4. Conclusions

In this work, we investigated the mappings for special functions on Cantor sets and special integral transforms via local fractional calculus, namely, the local fractional Fourier series, Fourier transforms, and Laplace transforms, respectively. These transformations were applied successfully to solve three local fractional differential equations, and the nondifferentiable solutions were reported.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.