Abstract and Applied Analysis
Volume 2013, Issue 1 284646
Research Article
Open Access

An Analytical Solution for Effect of Magnetic Field and Initial Stress on an Infinite Generalized Thermoelastic Rotating Nonhomogeneous Diffusion Medium

S. R. Mahmoud, 

Corresponding Author

S. R. Mahmoud

Mathematics Department, Science Faculty, King Abdulaziz University, Jeddah 21589, Saudi Arabia kau.edu.sa

Mathematics Department, Science Faculty, Sohag University, Sohag 82524, Egypt sohag-univ.edu.eg

Search for more papers by this author
First published: 26 December 2013
https://doi.org/10.1155/2013/284646
Citations: 3
Academic Editor: Hasan Ali Yurtsever

Abstract

The problem of generalized magneto-thermoelastic diffusion in an infinite rotating nonhomogeneity medium subjected to certain boundary conditions is studied. The chemical potential is also assumed to be a known function of time at the boundary of the cavity. The analytical expressions for the displacements, stresses, temperature, concentration, and chemical potential are obtained. Comparison was made between the results obtained in the presence and absence of diffusion. The results indicate that the effect of nonhomogeneity, rotation, magnetic field, relaxation time, and diffusion is very pronounced.

1. Introduction

Diffusion can be defined as the spontaneous migration of substances from regions of high concentration to regions of low concentration. There is now a great deal of interest in the study of this phenomenon due to its many applications in geophysics and industrial applications. Thermodiffusion in the solids is one of the transport processes which has great practical importance. Thermodiffusion in an elastic solid is due to the coupling of the fields of temperature, mass diffusion, and that of strain. This mater has attracted the attention of many researchers such as [1–5]. Wave propagation in rotating and nonhomogeneous media was studied by Abd-Alla et al. [6–8]. The extended thermoelasticity theory, introducing one relaxation time in the thermoelastic process, was proposed by Lord and Shulman [9]. In this theory, a modified law of heat conduction including both the heat flux and its time derivative replaces conventional Fourier’s law. The heat equation associated with this is a hyperbolic one and hence automatically eliminates the paradox of infinite speeds of propagation inherent in the coupled theory of thermoelasticity. This theory was extended by Dhaliwal and Sherief [10] to include the anisotropic case. Abd-Alla and Mahmoud [11] investigated the magneto-thermoelastic problem in rotating nonhomogeneous orthotropic hollow cylinder under the hyperbolic heat conduction model. Mahmoud [12] investigated wave propagation in cylindrical poroelastic dry bones.

Kumar and Devi [13] studied deformation in porous thermoelastic material with temperature dependent properties. Othman et al. [14] presented the study of the two-dimensional problems of generalized thermoelasticity with one relaxation time with the modulus of elasticity being dependent on the reference temperature for nonrotating and rotating medium, respectively. Kumar and Gupta [15] investigated deformation due to inclined load in an orthotropic micropolar thermoelastic medium with two relaxation times. The temperature-rate dependent theory of thermoelasticity, which takes into account two relaxation times, was developed by Green and Lindsay [16]. Abd-Alla et al. [17, 18] investigated radial vibrations in a nonhomogeneous orthotropic elastic medium subjected to rotation and gravity field. Sherief et al. [19] developed the generalized theory of thermoelastic diffusion with one relaxation time, which allows the finite speed of propagation waves. Sherief and Saleh [20] investigated the problem of a thermoelastic half-space in the context of the theory of generalized thermoelastic diffusion with one relaxation time. The reflection of SV waves from the free surface of an elastic solid in generalized thermoelastic diffusion was discussed by Singh [21]. Kumar and Kansal [22] discussed the propagation of Lamb waves in transversely isotropic thermoelastic diffusive plates. Thermomechanical response of generalized thermoelastic diffusion with one relaxation time due to time harmonic sources was discussed by Ram et al. [23]. Aouadi [24] examined the thermoelastic diffusion problem for an infinite elastic body with spherical cavity. Abd-Alla and Mahmoud [25] investigated analytical solution of wave propagation in nonhomogeneous orthotropic rotating elastic media. Othman et al. [26] discussed the effect of diffusion in a two-dimensional problem of generalized thermoelasticity with Green-Naghdi theory. Xia et al. [27] studied the influence of diffusion on generalized thermoelastic problems of infinite body with a cylindrical cavity. Deswal and Kalkal [28] studied the two-dimensional generalized electromagneto-thermoviscoelastic problem for a half-space with diffusion. Abd-Alla and Abo-Dahab [29] found the time-harmonic sources in a generalized magneto-thermo-viscoelastic continuum with and without energy dissipation. Mahmoud [30] discussed influence of rotation and generalized magnetothermoelastic on Rayleigh waves in a granular medium under effect of initial stress and gravity field. Abd-Alla et al. [31, 32] studied the generalized magneto-thermoelastic Rayleigh waves in a granular medium under the influence of a gravity field and initial stress.

In the present investigation, the temperature, displacements, stresses, diffusion, and concentration as well as chemical potential are obtained in the physical domain using the harmonic vibrations. Also, study of the interaction between the processes of elasticity, nonhomogeneity, rotation, magnetic field, initial stress, heat, and diffusion in an infinite elastic solid with a spherical cavity in the context of the theory of generalized thermoelastic diffusion is presented.

2. Formulation of the Problem

Consider a perfect electric conductor and linearized Maxwell equations governing the electromagnetic field in the absence of the displacement current (SI) in the form as in Kraus [33]. Applying an initial magnetic field vector in spherical coordinates (r, θ, ϕ), . One will consider a nonhomogeneous, isotropic medium, occupying the region a ≤ r ≤ b, where a is the radius of the spherical cavity. The strain tensor has the following components:
(1a)
(1b)
(1c)
(1d)
The cubical dilatation is given by (1/r2)(∂/∂r)(r2u), where the nonvanishing displacement component is the radial one ur = u(r, t). The elastic medium is rotating uniformly with an angular velocity , where is a unit vector representing the direction of the axis of rotation. The displacement equation of motion in the rotating frame has two additional terms: which is the centripetal acceleration due to time varying motion only, and is the Coriolis acceleration, where . Following Sherief’s theory of generalized thermoelastic diffusion [19] and Sherief and Saleh [20], one is going to study an isotropic nonhomogeneous elastic medium which suffers thermal shock. Due to spherical symmetry, the stress-displacement-temperature-diffusion relation or constitutive equations are given by
(2a)
(2b)
The chemical-displacement-temperature-diffusion relation is given by
(3)
The governing equation for an isotropic nonhomogeneous elastic solid with generalized magneto-thermoelastic diffusion under effect of rotation is given by
(4)
where λ and μ are Lame’s elastic constants, δij is Kronecker’s delta, P1 is the initial stress, ρ is the density of the medium, and is defined as Lorentz’s force which may be written as
(5)
where μe is the magnetic permeability, is the magnetic field vector, is the electric current density, is the displacement vector, and t is the time.
Equation of heat conduction is given by
(6)
where the Laplacian operator ∇2 is given by ∇2 = (∂2/∂r2) + (2/r)(∂/∂r) and , h0 is the coefficient of linear diffusion expansion, K is the thermal conductivity, θ is the absolute temperature, θ0 is the initial uniform temperature, and |(θ − θ0)/θ0| ≪ 1.
Equation of conservation of mass diffusion may be written as
(7)
where τ is the diffusion relaxation time, τ0 is the thermal relaxation time, αt is the coefficient of linear thermal expansion, and θ0 is constant, where β1 = (3λ + 2μ)αt, β2 = (3λ + 2μ)αc,   σij are the components of the stress tensor, τij are the components of stress tensor, b and c are the measures of thermodiffusion and diffusive effects, C is the concentration, Cv is the specific heat at constant strain, D is the diffusive coefficient, and eij are the components of the strain tensor. The thermal relaxation time τ0 will ensure that the heat conduction equation will predict finite speed of heat propagation. The diffusion relaxation time τ, which will ensure the equation satisfied by the concentration C, will also predict finite speed of propagation of matter from one medium to the other.

3. Dimensionless Quantities

Introduce the following nondimensional parameters:
(8)
The elastic constants λ,  μ and the density ρ of nonhomogeneous material in form [32] are as follows:
(9)
Using the above non-dimensional parameters and (9) in (10)–(14), the non-dimensional system becomes
(10)
(11)
(12)
(13a)
(13b)
(13c)
 
(14)
where
(15)

4. Boundary Conditions

The nonhomogeneous initial conditions are supplemented by the following boundary conditions. The cavity surface is traction free:
(16a)
The cavity surface is subjected to a thermal shock
(16b)
where H(t) is the Heaviside unit step function. The chemical potential is also assumed to be a known function of time at the cavity surface:
(16c)
The displacement function is as follows:
(16d)

5. Solution of the Problem

In this section, one obtains the analytical solution of the problem for a spherical region with boundary conditions by taking the harmonic vibrations. One assumes that the solution of (10)–(12) as follows:
(17a)
(17b)

where e = (∂u/∂r) + (2u/r) = (1/r2)(∂/∂r)(r2u).

Substituting (17a) and (17b) into (10)–(12) yields
(18)
(19)
(20)
Applying the operator Laplacian operator ∇2 to (18), we obtain
(21)
From (19)–(21), we obtain
(22)
where
(23)
Equation (22) can be factorized as
(24)
where , , and are the roots of the characteristic equation
(25)
The solution of (24) which is bounded at infinity is given by
(26)
where Bj, , and are parameters depending only on ω and K1/2 is the modified spherical Bessel function of the second kind of order 1/2. Compatibility between (26) along with (19) and (20) will give rise to
(27)
Substituting (26) into (17a) and (17b), we obtain
(28)
(29)
(30)
Integrating both sides of (29) from r to infinity and assuming that u(r, t) vanishes at infinity, we obtain
(31)
From (13a), (13b), and (13c)-(14), we get
(32)
Using the boundary conditions, we get
(33)

6. Particular Case

If we neglect the initial stress and diffusion effects by eliminating (3) and (8) and putting P1 = β2 = C = 0 in (4) and (6), we get (T,  e), u(r, t), σrr, σϕϕ, and σθθ:
(34)
where
(35)
Using the boundary conditions, we obtain
(36)

7. Numerical Results and Discussion

For the purposes of numerical evaluations. The copper material was chosen. The constants of the problem given by Aouadi [24], Sokolnikoff [34] and Thomas [35] are
(37)
Using the above values, we get μe = 1, θ0 = 1, P0 = 1, a = 2, ω = 9.5, H = 0.7 × 10−5, τ0 = 0.1, and τ = 0.2. The values of radial displacement u, temperature distribution θ, concentration C, stresses σrr, σϕϕ, and chemical potential distribution P for thermoelastic diffusion and thermoelasticity are studied for force thermal source and chemical potential source. The output is plotted in Figures 1–10. Figure 1 shows that the values of chemical potential distribution P have oscillatory behavior with diffusion in the whole range of radius r. The effects of nonhomogeneity m, rotation Ω, time t and relaxation time τ0 on chemical potential distribution is shifting from the positive into the negative gradually with the radius r. Figure 2 shows that the value of concentration distribution C has oscillatory behavior for diffusion in the whole range of radius r under the effects of nonhomogeneity, rotation, and relaxation time, while it is decreasing with an increase of nonhomogeneity m. In these figures, it is clear that the distribution has a nonzero value only in the bounded region of space for t = 0.15 where the infinite speed of propagation is inherent. The effects of nonhomogeneity, rotation Ω, time t, and relaxation time τ0 on concentration distribution is shifting from the positive into the negative gradually. This indicates that the equations are satisfied by the concentration C which predict a finite speed of propagation of matter from first medium to another one. Figure 3 shows that the value of temperature distribution θ has an oscillatory behavior for thermoelastic diffusion in the whole range of the radius r, while the solution is notably different inside the sphere. This is due to the fact that, the thermal waves in the coupled theory travel with an infinite speed of propagation as opposed to finite speed in the generalized case. The effects of nonhomogeneity, rotation Ω, time t and relaxation time τ0 on temperature distribution shift from the positive into the negative gradually. This indicates that the heat propagates as a wave with finite velocity. Figure 4 shows that the value of radial displacement u has oscillatory behavior with diffusion in the whole range of radius r. These figures indicate that the medium along r undergoes expansion deformation due to the thermal shock, while the other one shows the compressive deformation. The effect of nonhomogeneity, rotation Ω, and relaxation time τ0 on radial displacement becomes large. Increasing the nonhomogeneity, the radial displacement is shifted upward from negative values to positive values. At a given instant, the radial displacement is finite which is due to the effect of nonhomogeneity, rotation, time, and relaxation time. Figures 5 and 6 show the variations of the radial stress σrr and tangential stress σϕϕ with respect to the radius r, respectively. The values of radial stress and tangential stress are increased and decreased due to the diffusion in a nonuniform behavior for all values of the radius r. For the values of σrr and σϕϕ, depicting the effect of nonhomogeneity, diffusion, rotation, and relaxation time, it is shown that the radial stress is compressive in its nature.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Variation of chemical potential P with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Variation of chemical potential P with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Variation of concentration C with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Variation of concentration C with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Variation of temperature θ with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Variation of temperature θ with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Variation of displacement u with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Variation of displacement u with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Variation of radial stress σrr with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Variation of radial stress σrr with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Variation of tangential stress σϕϕ with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Variation of tangential stress σϕϕ with radius r (thermoelastic diffusion nonhomogeneity medium).
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Variation of displacement u with radius r (thermoelastic nonhomogeneity medium).
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Variation of temperature θ with radius r (thermoelastic nonhomogeneity medium).
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Variation of radial stress σrr with radius r (thermoelastic nonhomogeneity medium).
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Variation of tangential stress σϕϕ with radius r (thermoelastic nonhomogeneity medium).

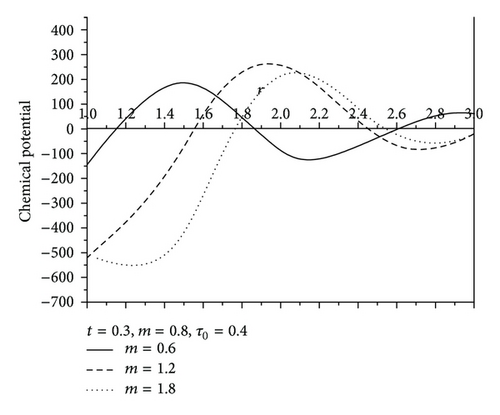
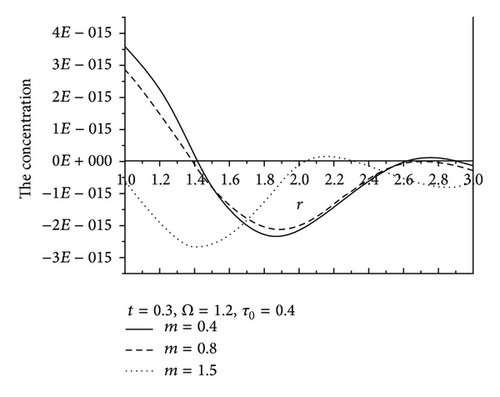
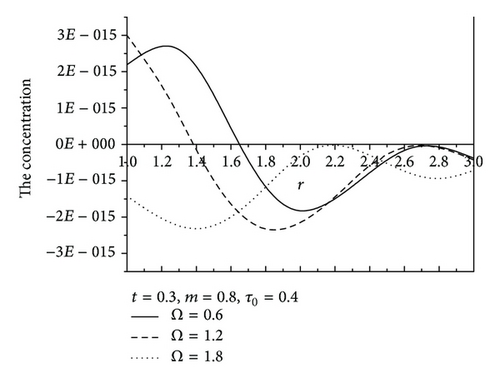
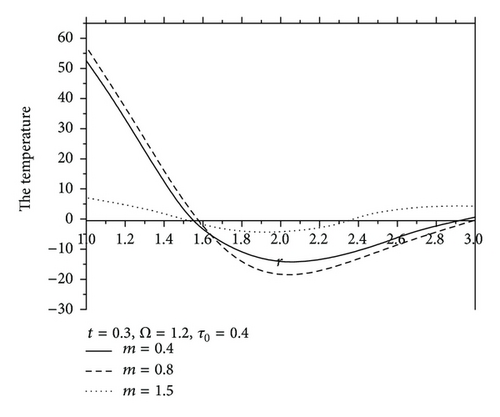
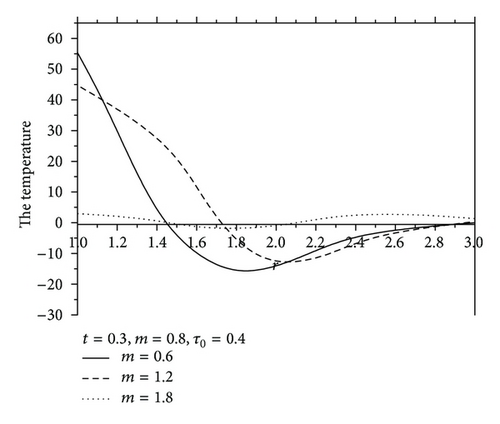
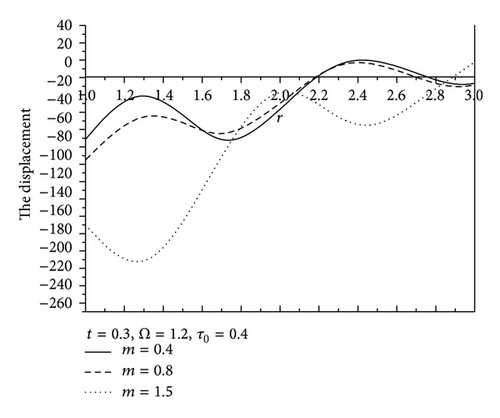
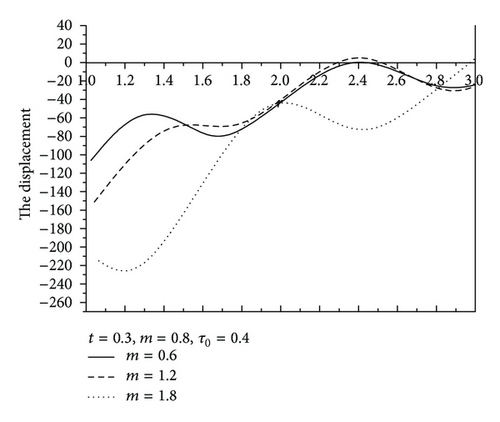
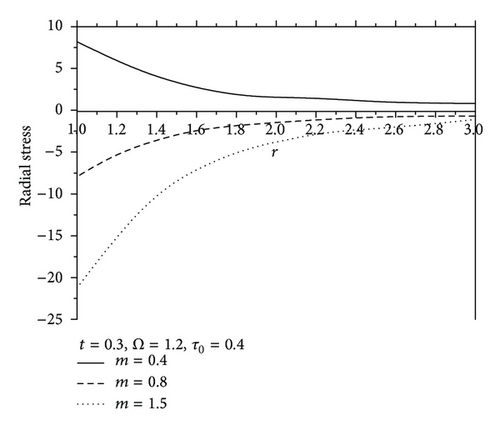
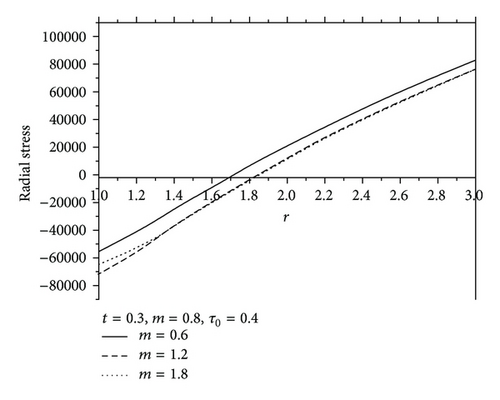
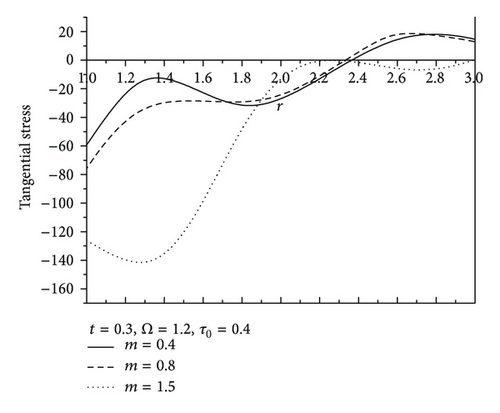
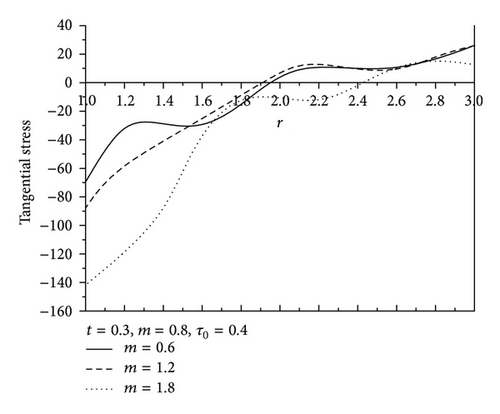
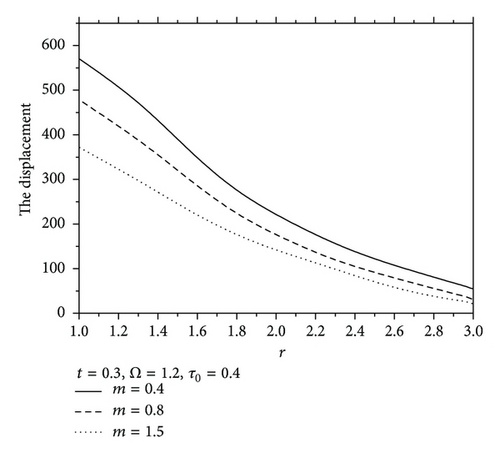
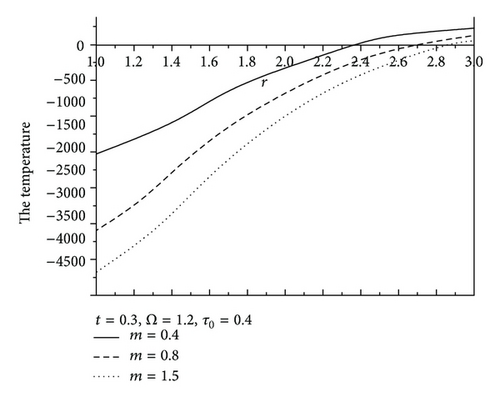
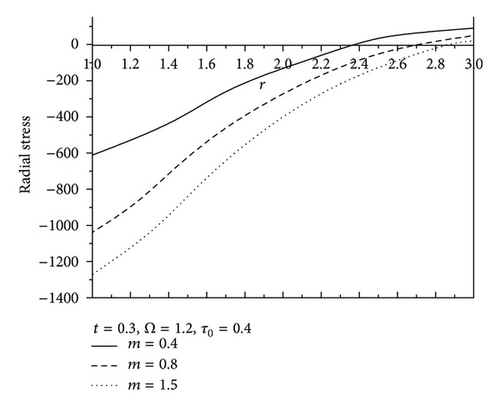
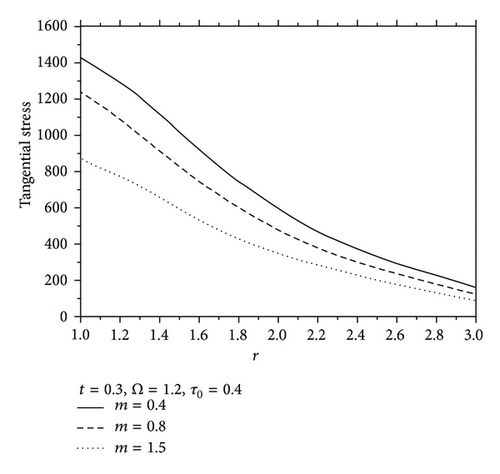
Figure 7 shows the values of radial displacement u in thermoelastic medium without diffusion. This figure indicates clearly that the radial displacement at the cavity surface tends to zero which agrees with the boundary conditions prescribed. This coincides with the mechanical boundary condition of the cavity, in case of fixed surface. Figure 8 shows the values of temperature distribution θ without diffusion in the whole range of radius r. It was found that the values of θ under effect of nonhomogeneity and rotation Ω are increase with an increase of nonhomogeneity and rotation Ω but are decreasing with the increase of the values of m. Figures 9 and 10 show the values of radial stress σrr and the tangential stress σϕϕ without diffusion in the whole range of radius r, respectively. It was found that the values of σrr under the effects of nonhomogeneity m and rotation Ω are increasing with an increase of the values of nonhomogeneity m and rotation Ω, while the values of σrr are decreasing with an increase of nonhomogeneity m, while the tangential stress σϕϕ is decreasing with the increase of the values of nonhomogeneity m and rotation Ω, but the values of σϕϕ are increasing with an increase of m. Due to the complicated nature of the governing equations of the generalized magneto-thermoelastic diffusion theory, the done works in this field are unfortunately limited. The method used in this study provides quite a success in dealing with such problems. This method gives exact solutions in the elastic medium without any restrictions on the actual physical quantities that appear in the governing equations of the considered problem.

8. Conclusions

The results presented in this paper will be very helpful for researchers concerned with material science, designers of new materials, and low-temperature physicists, as well as for those working on the development of a theory of hyperbolic propagation of hyperbolic thermodiffusion. Study of the phenomenon of nonhomogeneity, rotation, magnetic field, and diffusion is also used to improve the conditions of oil extractions. It was found that, for values of rotation and nonhomogeneity, the coupled theory and the generalization give close results. The case is quite different when we consider small value of rotation and nonhomogeneity. Comparing Figures 1–6 in case of thermoelastic diffusion medium with the Figures 7–10 in case of thermoelastic medium, it was found that u, σrr, σϕϕ, C, and P have the same behavior in both media. But with the passage of nonhomogeneity and rotation, the numerical values of u, σrr, σϕϕ, C, and P in thermoelastic diffusion medium are large in comparison with those in thermoelastic medium due to the influences of nonhomogeneity, magnetic field, rotation, and mass diffusion.

Acknowledgment

This article was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. The author, therefore, acknowledge with thanks DSR technical and financial support.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.