Abstract and Applied Analysis
Volume 2013, Issue 1 206942
Research Article
Open Access

Two-Dimension Hydrodynamic Dispersion Equation with Seepage Velocity and Dispersion Coefficient as Function of Space and Time

Abdon Atangana, 

Corresponding Author

Abdon Atangana

Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein 9300, South Africa ufs.ac.za

Search for more papers by this author
S. C. Oukouomi Noutchie, 

S. C. Oukouomi Noutchie

Department of Mathematical Sciences, North-West University, Mafikeng Campus, Mmabatho 2735, South Africa nwu.ac.za

Search for more papers by this author
First published: 20 June 2013
https://doi.org/10.1155/2013/206942
Citations: 1
Academic Editor: L. Jódar

Abstract

The contamination through the geological formation cannot move and disperse with the same speed and dispersion coefficient, respectively, due to the variability of the geological formation. This paper is therefore first devoted to the description of the hydrodynamic advection dispersion equation with the seepage velocity and dispersion coefficient as function of space and time. Secondly the equation is solved via two analytical techniques: the homotopy decomposition method and the differential transform method. The numerical simulations of the approximated solutions are presented.

1. Introduction

Most of the Earth’s liquid freshwater is found, not in lakes and rivers, but is stored underground in conglomerations of voids, called aquifers, and present in the geological formations constituting the earth’s mantle, where they act as reservoirs of water for rivers and streams, especially during periods of drought or low rainfall—a phenomenon commonly called baseflow. This resource, conventionally referred to as groundwater, therefore forms an essential, in fact major, component of the fresh water resources, as illustrated by the fact that that nearly two billion people depend directly on groundwater or their drinking water, while 40% of the world’s food is produced on farmlands irrigated with groundwater [1].

One reason why groundwater so often constitutes the main source of drinking water in many cities and towns around the world is because it is frequently present in sufficient quantities at the point of demand. However, this seemingly advantage may sometimes be its greatest disadvantage, especially in situations where the groundwater occurs at shallow depths and the area overlying the aquifer is populated densely. This problem is particularly relevant in the present technological age to its vast quantities of waste that is often disposed in an uncontrolled manner. Since space, time, and mass are measurable, and numbers form the basis of all mathematics, the question arises if it is not possible to combine the power of human reason with well-planned observations and describe natural phenomena in abstract mathematical terms? This question leads us to the mathematical formulation of the flow of subsurface water in the geological formations. The development of a theory for natural phenomenon can be briefly summarized in four steps [2, 3].

Apply the rules of mathematical analysis to the observables and try to establish a framework, or hypothesis, able to predict the behaviour of the phenomenon, under different conditions from those used in establishing the hypothesis. The main effort is to establish a suitable mathematical relation between different observables, or what [4] calls a mathematical model for the observables. An ideal mathematical model should not only provide links between different observables, but also lead to a better understanding of the phenomenon. The attractiveness of this approach is that the mathematical model could, in principle, be used to investigate the future behaviour of a given phenomenon and under various conditions. For simplicity, it is always assumed that, the seepage velocity retardation factor and the dispersion coefficient appearing are the mathematical equation describing the movement of contamination in groundwater as constants. However, in the real world observation, these coefficients depend on space and time. One therefore needs to include such behaviour in the mathematical formulation. This paper is therefore devoted to the discursion underpinning the effect of variation in time space of the seepage velocity and dispersion coefficient on one hand, and on the other hand a possible analytical solution of this equation.

2. Mathematical Formulation

The mathematical model, discussed below, has been used extensively in the studies of groundwater pollution problems, with satisfactory results. A relatively complete set of one-dimensional analytical solutions for convective-dispersive solute equations has been recently published by [5]; here we will review a case having a practical application. Let us consider a two-dimensional model consisting of and infinitely ling homogenous isotropic porous media with steady-state uniform flow with seepage velocity v. We inject a particular chemical from one end of the model for a period of time t0 such that the input concentration varies as an exponential function of time [5]. The value of that chemical concentration at any time t and at a distance x from the injection boundary, allowing for the decay and adsorption, may be obtained from the solution of the following set of equations [5]:
()
where D is the dispersion coefficient and R is the retardation factor and subject to the initial condition:
()
which means that the system is initially free of that chemical, γ and c0 are constants, and λ is the radioactive decay constant. And boundaries conditions:
()
In order to include explicitly the variation of the seepage velocity and dispersion coefficient into the mathematical formulation, we replace the constants coefficients R,  D, and v of (1) by the functions R(x, y, t),  D(x, y, t), and v(x, y, t) to obtain
()
To satisfy the physical behaviour of the aquifer, there exist positives constants C1, C2, and C3 such that
()

3. Analytical Solutions

Environmental phenomena, such as groundwater pollution, are highly complex phenomena, which do not lend themselves readily to analysis of analytical models. The discussion presented in this section will therefore be devoted to the derivation of analytical solution to the advection dispersion equation (1). As V. M. Alexandrov wrote in the foreword of a popular science book “Asymtotology: ideas, methods, and applications [sic]”, asymptotic methods belong to the, perhaps, the most romantic area of modern mathematics [6]. Though computer science is growing very fast and numerical simulation is applied everywhere, nonnumerical issues will still play a large role [7–11].

There exist some alternative analytical asymptotic approaches, such as the nonperturbative method [12], modified Lindstedt-Poincare method [13], variational iteration method [14], Adomian decomposition method [14], homotopy perturbation method [15], and book-keeping artificial parameter perturbation method [15]. Recently to solve the groundwater flow equation, Atangana and Botha proposed a modified decomposition method called homotopy decomposition [16]. In this section we make use of two different methods including the HDM and DTM to derive approximate solution of (1). We will start with HDM.

3.1. Useful Tools for the Homotopy Decomposition Method [17–19]

To accommodate readers that are not acquainted with this modified form of decomposition method, we present in this section the basic methodology of the method. To illustrate the fundamental design of this technique, we consider a universal nonlinear nonhomogeneous partial differential equation with initial conditions of the following form:
()
subject to the initial condition:
()
where h is a known function, N is the general nonlinear differential operator, and L represents a linear differential operator. The first step of the method here is to apply the inverse operator ∂m/∂tm of on both sides of (1) to obtain
()
The multi-integral in (2) can be transformed to
()
so that (8) can be reformulated as
()
Using the Homotopy scheme the solution of the above integral equation is given in series form as
()
and the nonlinear term can be represented as
()
where β ∈  (0,  1] is an embedding parameter. Pn(R) is the polynomials that can be engendered by
()
The homotopy decomposition method is achieved via the polished combination of decomposition method with Abel’s integral and is given by
()
With
()
matching up to the expressions of similar powers of β, we can get hold of solutions of assorted orders. The early estimate of the approximation is K(x, t). It is significant to draw attention to the fact that the early estimate is the Taylor series of order m of the exact solution.

3.2. Differential Transform Method (DTM) [17, 20–22]

The necessary definitions of the three-dimensional transform are shown. Given a w function which has three components such as x, y, t, the three-dimensional differential transform function of the function w(x, y, t) is defined as
()
where w(x, y, t) is the original function and W(k, h, m) is the transform function.
The inverse differential transform of w(k, h, m) is defined as
()
from (16) and (17) it can be concluded that
()
Some fundamental mathematical operators performed by three-dimensional differential transform methods are listed below [20]:
  • (1)

    if w(x, y, t) = W1(x, y, t) ∓ W2(x, y, t), then W(k, h, m) = W1(k, h, m) ∓ W2(k, h, m),

  • (2)

    if w(x, y, t) = cw1(x, y, t), then W(k, h, t) = cW1(k, h, t) where c is a constant,

  • (3)

    if w(x, y, t) = d1w1(x, y, t)/dx1, then W(k, h, t) = (k + 1)W1(k + 1, h, m),

  • (4)

    if w(x, y, t) = d1w1(x, y, t)/dy1, then W(k, h, t) = (h + 1)W1(h + 1, k, m),

  • (5)

    if w(x, y, t) = d1w1(x, y, t)/dt1, then W(k, h, t) = (m + 1)W1(m + 1, k, h),

  • (6)

    if w(x, y, t) = w1(x, y, t)w2(x, y, t), then .

4. Applications

In this section, we apply these methods for solving the two-dimension hydrodynamic dispersion equation with seepage velocity and dispersion coefficient as function of space and time.

Since 0 < R(x, y, t) ≤ C1, we first divide (1) by R(x, y, t) and let
()
to obtain
()
Applying the HDM to the above equation yields
()
Following the DTM method we supposed that the solution of (1) is in the form of
()
with
()
so that
()

Example 1. Let us consider in (1) the following coefficients:

()
The theoretical parameters used in this simulation are c0 = 100,  γ = 0.86,  λ = 1.

The following figure shows the numerical simulations of the approximated solutions obtained via HDM and DTM.

Figures 1 and 2 show the numerical simulation of the approximate solution via HDM and DTM, respectively. Here we fixed y = 2 and we consider the concentration to be a function of x and t. It can be observed that both methods give pretty much the same results for the first four components of the series solution.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Simulation of the approximate solution obtained via HDM for a fixed y  =  2.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Simulation of the approximate solution obtained via DTM for a fixed y  =  2.

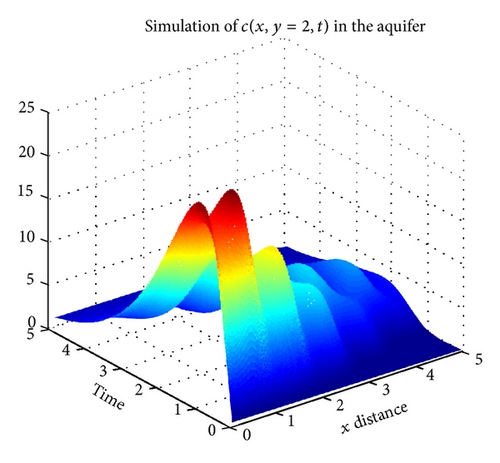
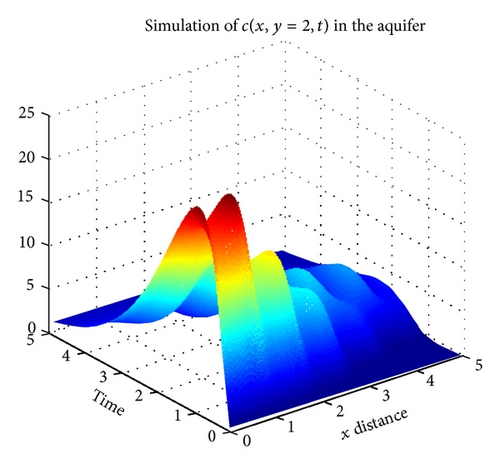
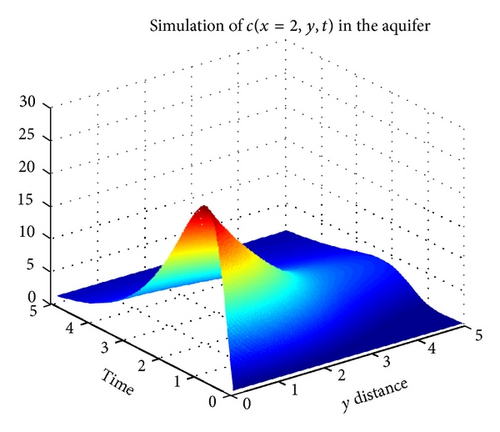
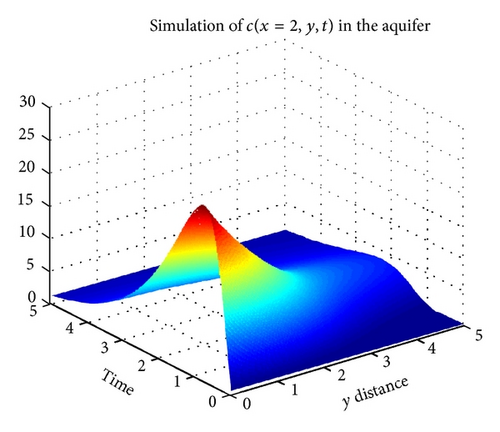
Figures 3 and 4 show the numerical simulation of the approximate solution via HDM and DTM, respectively. Here we fixed x = 2 and we consider the concentration to be a function of x and t.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Simulation of the approximate solution obtained via HDM for a fixed x  =  2.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Simulation of the approximate solution obtained via DTM for a fixed x  =  2.

Figures 5 and 6 are the contour plot obtained via Mathematica. These figures show the possible pathway taken by the pollution through the geological formation called aquifer.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Contour plot of the approximated solution in x-direction for fixed y.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Contour plot of the approximate solution in y-direction for fixed x.

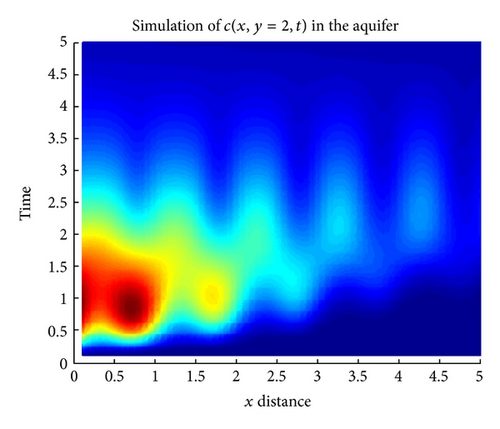
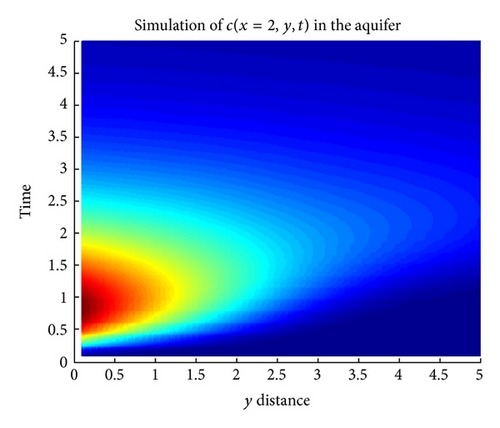
Figure 7 shows the contour plot of the approximate solution as a function of x and y for a fixed time. In practice this figure shows the behaviour of the contamination through the geological formation for a fixed time t  =  10. The figure shows that since the seepage velocity and the dispersion coefficient are function of space, the pollution will not have the same intensities everywhere in the aquifer. There will be certain place in the aquifer with more pollution than other, depending on the velocity and the dispersion coefficients associated.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Contour plot of the approximated solution for a fixed time t  =  2.

5. Discussion and Conclusion

Natural geological deposits with highly contrasting permeability may form mobile and relatively immobile zones, where the potential mass exchange between mobile and immobile zones results in a wide time distribution for solute trapping. The transport process in groundwater is, by its very nature, always in contact with the matrix of an aquifer. There is thus a possibility that the solutes may interact with the rock matrix and one another. A true mathematical model for groundwater pollution must therefore be able to account for interactions between the dissolved solids and matrix of the aquifer. It will thus be advantageous to look at the nature of the interactions between dissolved solids and a porous medium that may be expected in groundwater pollution. Experimental evidence indicates that when a dissolved solid comes in contact with the matrix of a porous medium, it may (a) pass through the medium with no apparent effect, (b) be absorbed by the porous matrix, and (c) react with the porous matrix and other substances dissolved in the fluid. The dissolved solids encountered in porous flow are, for this reason, often classified as conservative, nonconservative, and reactive tracers [22]. This behaviour implies that the quantity of dissolved solids in a porous medium depends not only on the flow pattern, but also on the nature of the porous matrix and the solution. These situations (a), (b), and (c) can be characterized efficiently by the time-nonlocal model, including the hydrodynamic dispersion equation with seepage velocity and dispersion coefficients as function of space and time as described by Figure 5. If the high-permeable material tends to form preferential flow paths, such as the interconnected paleochannels observed in alluvial depositional systems, then the solute transport may show a heavy leading edge, which can be described by the hydrodynamic dispersion equation with seepage velocity and dispersion coefficients as function of space and time.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.