Journal of Computational Methods in Physics
Volume 2013, Issue 1 174806
Research Article
Open Access

Quantitative Modeling of Faceted Ice Crystal Growth from Water Vapor Using Cellular Automata

Kenneth G. Libbrecht, 

Corresponding Author

Kenneth G. Libbrecht

Department of Physics, California Institute of Technology, Pasadena, CA 91125, USA caltech.edu

Search for more papers by this author
First published: 04 December 2013
https://doi.org/10.1155/2013/174806
Academic Editor: Xavier Ferrieres

Abstract

We describe a numerical model of faceted crystal growth using a cellular automata method. The model was developed for investigating the diffusion-limited growth of ice crystals from water vapor, when the surface boundary conditions are determined primarily by strongly anisotropic molecular attachment kinetics. We restricted our model to cylindrically symmetric crystal growth with relatively simple growth morphologies, as this was sufficient for making quantitative comparisons between models and ice growth experiments. Overall this numerical model appears to reproduce ice growth behavior with reasonable fidelity over a wide range of conditions. More generally, the model could easily be adapted for other material systems, and the cellular automata technique appears well suited for investigating crystal growth dynamics when strongly anisotropic surface attachment kinetics yields faceted growth morphologies.

1. Introduction

The formation of crystalline structures during solidification yields a remarkable variety of morphological behaviors, resulting from the often subtle interplay of nonequilibrium physical processes over a range of length scales. In many cases, seemingly small changes in surface molecular structure and dynamics at the nanoscale can produce large morphological changes at all scales. Some examples include free dendritic growth from the solidification of melts, where small anisotropies in the interfacial surface energy govern the overall characteristics of the growth morphologies [1, 2], whisker growth from the vapor phase initiated by single screw dislocations and other effects [3], the formation of porous aligned structures from directional freezing of composite materials [4], and a range of other pattern formation systems [5, 6]. Since controlling crystalline structure formation during solidification has application in many areas of materials science, much effort has been directed toward better understanding the underlying physical processes and their interactions.

We have been exploring the growth of ice crystals from water vapor in an inert background gas as a case study of how complex faceted structures emerge in diffusion-limited growth. Although this is a relatively simple monomolecular physical system, ice crystals exhibit columnar and plate-like growth behaviors that depend strongly on temperature, and much of the phenomenology of their growth remains poorly understood [7–9]. Ice has also become something of a standard test system for investigating numerical methods of faceted crystal growth [10, 11]. A better understanding of ice crystal formation yields insights into the detailed molecular structure and dynamics of the ice surface, which in turn contributes to our understanding of many environmental and biological processes involving ice [12–14].

In our investigation of how surface energy and attachment kinetics affect ice growth dynamics, we needed a quantitative numerical model that would allow us to “grow” model crystals for comparison with experimental measurements of growth rates and morphologies. Although proven numerical methods for modeling diffusion-limited growth have been available for years, many of the existing methods are ill suited for modeling ice growth behavior. For example, phase-field [15, 16] and front-tracking [17] methods have demonstrated the ability to accurately model diffusion-limited growth for the case of fast attachment kinetics and a weakly anisotropic surface energy, which is typical of solidification from the melt. These systems typically yield unfaceted dendritic structures, however, in contrast to strongly faceted ice structures. Early models for the growth of faceted crystals [18, 19] were generally too limited to allow quantitative comparisons with ice growth data.

Modeling diffusion-limited growth in systems with strong surface anisotropies has proven difficult, and only recently have researchers demonstrated robust techniques capable of generating structures that are both faceted and dendritic. Gravner and Griffeath [10] described an especially promising cellular automata simulator that solves the diffusion equation by nearest neighbor relaxation, including a set of parameterized nearest neighbor rules to define the boundary conditions at the crystal interface. This method yields a deterministic dendritic growth behavior in which faceting follows the symmetry of the predefined numerical grid.

Barrett et al. [11] also developed a robust adaptive mesh technique that generated faceted dendritic crystal growth patterns. In this work the authors found that a strongly anisotropic surface energy was required to produce faceted dendritic growth, while anisotropic attachment kinetics alone were not sufficient to reproduce this behavior. We have suggested that the ice case is more likely described by the opposite characteristics; an essentially isotropic surface energy together with strongly anisotropic attachment kinetics, the latter dominating the growth behavior [20]. In fact, the relative roles played by these two physical effects is not yet known with certainty.

The relative merits of different computational methods for modeling diffusion-limited growth in the presence of strong surface anisotropies are not presently well understood, and this is an area of current research. Moreover, our knowledge of the surface physics governing the growth of faceted materials is itself rather poor, including the relative contributions of the anisotropies in surface energy and attachment kinetics in different materials. In our experience, progress on both these research fronts is linked: better modeling methods allow better interpretation of growth experiments, and this in turn leads to a better understanding of the surface physics input into the models.

Below we describe a cellular automata method for modeling diffusion-limited growth in the presence of strongly anisotropic molecular attachment kinetics, focusing on ice growth from water vapor. Our treatment of the surface boundary conditions derives from known surface physics and thus replaces the somewhat unphysical parameterization adopted in [10]. We have found our model to be robust, well behaved, computationally straightforward, and quite flexible for exploring ice growth behaviors. The 2D cylindrically symmetric model described below has been especially useful for investigating the simple growth morphologies often produced in experiments, allowing the rapid generation of hundreds of model crystals with different input assumptions. This model has allowed us to better examine the surface physical processes governing ice growth rates, and it allows straightforward adaptation for use in other investigations involving faceted diffusion-limited crystal growth.

2. Modeling Ice Crystal Growth

A variety of physical processes are involved in the growth of ice crystals from water vapor in an inert background gas. Particle diffusion plays a large role, as water vapor molecules must diffuse through the gas to reach the growing crystal. Heat diffusion is also present, since the latent heat generated by condensation must be removed from the crystal. Surface energy effects are present via the Gibbs-Thomson effect, and surface attachment kinetics govern the placement of water molecules into the ice crystal lattice. If the background gas is not inert, surface chemical effects may also be significant.

Our focus here will be on ice growth under near atmospheric conditions, which allows a number of simplifications in the problem. Particle transport is described by the diffusion equation:
()
using the notation in [7], where c(x) is the water molecule number density surrounding the crystal and D is the diffusion constant. The timescale for diffusion to adjust the vapor concentration in the vicinity of a crystal is τdiffusion ≈ R2/D, where R is a characteristic crystal size. This is to be compared with the growth time, τgrowth ≈ 2R/vn, where vn is the growth velocity of the solidification front normal to the surface. The ratio of these two timescales is the Peclet number, pPeclet = Rvn/2D. For typical growth rates of ice crystals, we find pPeclet≲10−5, which means that diffusion adjusts the particle density around the crystal much faster than the crystal shape changes. In this case the diffusion equation reduces to Laplace’s equation, ∇2c = 0, which must be solved with the appropriate boundary conditions. Using this slow-growth limit simplifies the problem considerably in comparison to much of the literature on diffusion-limited solidification.
It is convenient to work with the supersaturation, σ(x) = [c(x) − csat ]/csat , where csat  is the equilibrium vapor density above a flat ice surface. Then the diffusion equation becomes
()
and the continuity equation at the interface gives
()
where csolid = ρice/m is the number density for ice, ρice is the ice density, and m is the mass of a water molecule. For the outer boundary one typically assumes a constant supersaturation σ∞.

Including latent heating of the crystal would mean solving a double diffusion problem, involving both particle and heat diffusion simultaneously, complicating the problem considerably. However, since the thermal conductivity of ice is much higher than that of air, heating raises the temperature of the crystal roughly uniformly, at least for simple morphologies, which increases the effective csat  for the crystal. Thus the main effect of heating can be approximated by a relatively small rescaling of σ∞ [7]. Furthermore, many experiments are done using ice crystals resting on a thermally conducting substrate, and in this case the effects of latent heating are essentially negligible [7]. For these reasons we have ignored latent heating in the present model, with the understanding that heating effects may be important in some experimental circumstances.

The attachment kinetics are usually defined by writing the growth velocity normal to a flat surface in terms of the Hertz-Knudsen formula [7]:
()
where σsurf is the supersaturation at the surface, and this equation defines the “kinetic velocity” vkin. The parameter α is known as the condensation coefficient, and it embodies the surface physics that governs how water molecules are incorporated into the ice lattice, collectively known as the attachment kinetics. The attachment kinetics can be quite complex, so in general α will depend on T and σsurf and perhaps surface structure and geometry, surface chemistry, and so forth. If molecules striking the surface are instantly incorporated into it, then α = 1; otherwise we have α ≤ 1. A faceted growth form usually indicates that the growth is limited by attachment kinetics, so α < 1 on faceted surfaces. For a molecularly rough surface we expect α ≈ 1.

One should note that the growth parameterization in terms of α assumes that the attachment kinetics can be described as an intrinsically local process, which may not always be a valid assumption. For the ideal case of an infinite, defect-free surface, this parameterization must be valid, since in this limit it is little more than a mathematical redefinition. Nonlocal effects, however, such as surface transport between facets, could make the parameterization invalid in some circumstances.

For example, it has been shown that the assumption of a well-defined attachment coefficient is not valid for the growth of mercury whiskers [21, 22], since a value of α ≫ 1 would be required at the whisker tip. In this case the tip growth is enhanced by surface diffusion of molecules along the faceted sides of the whisker and onto the growing tip, which is an intrinsically nonlocal process. The Schwoebel-Ehrlich effect provides a potential barrier that normally inhibits surface diffusion around corners [23, 24], the mercury case being an exception. Experimental evidence supports the hypothesis that α ≤ 1 for ice crystal growth and that nonlocal growth effects can be neglected [7], but this is not known with certainty.

For the remainder of our discussion we will assume that (1) ice growth is in the limit pPeclet ≪ 1; (2) latent heating of the crystal is negligible; (3) the surrounding environment and the crystal are at a constant temperature and pressure, so csat  and D have a single value throughout the system; and (4) the attachment coefficient α is well defined at the surface. We retain that α may depend on temperature, the surface supersaturation, and the orientation of the surface relative to the crystal axes. We also retain that α may depend on the local crystal structure [25].

Our overarching goal was to develop a basic numerical modeling tool that would allow us to compare different theoretical pictures of surface growth processes with experimental measurements of ice growth rates over a range of conditions. Our focus was therefore on producing quantitative calculations of crystal growth rates and morphologies from well-defined physical inputs, including known diffusion rates through the surrounding gas, known initial sizes and morphologies of test crystals, and theoretical parameterizations of surface attachment kinetics and surface energy effects. We limited our calculations to the growth of fairly simple morphologies, as these are best suited for extracting information about surface growth processes from experimental data.

3. The 1D Spherical Model

It is useful to begin by examining the simplest case of the growth of spherical crystals. Starting with the diffusion equation in spherical coordinates,
()
and assuming a one-dimensional array of pixels with uniform size, Δr gives the propagation equation
()
where
()
We typically choose Δτ = 1/2, as larger values can lead to numerical instabilities, and this gives
()

3.1. Boundary Conditions

In this spherical model we are essentially assuming a single spherical “facet” for the interface, with the surface growth rate given in (4). We let all pixels with radial index i ≤ iice be ice, and we refer to the next pixel, with i = iice + 1, as a “boundary” pixel. In one time step the ice surface grows an amount δr = vΔt, and this growth extracts a total mass
()
from the boundary pixel shell, reducing the supersaturation in that shell by
()
where rbound is the radius of the center of the boundary pixel. Thus we can write
()
for the mass drain of the boundary pixel, where
()
T15 = −15°C and Dair ≈ 2 × 10−5 m2/sec is the diffusion constant in air at a pressure of one bar.
We combine (6) and (11) to create a total propagation algorithm for the boundary pixel
()
where
()
To describe the ice growth, we assume that a boundary pixel starts out with zero accumulated mass, and it turns into an ice pixel when it has accumulated a mass . After one time step, it accumulates the mass in (9), giving
()
Thus we define an accumulated mass parameter λ for the boundary pixel, where λ starts at zero and after each timestep becomes
()
where
()
When λ becomes greater than one, the boundary pixel turns to ice.

3.2. Adaptive Time Steps

In practice (17) gives an exceedingly slow growth rate, because csat /cice is quite small, so we speed up the code by using
()
where Λ is an adjustable parameter. Note that the number of steps needed to advance one pixel is (ασΔλ)−1, so the growth velocity is
()
We optimize the speed of the code by increasing Λ as much as possible, subject to criteria that limit the resulting errors in the growth behavior. Our first criterion is that it should take more than N0 time steps to change a boundary pixel from air to ice, where typically N0 ≈ 10, and this gives
()
We also want the Peclet number to be much less than unity, so the growth is slower than the time it takes for the supersaturation field to stabilize, as described above, and this gives
()
where R is the crystal radius. We use pPeclet,max  = 1/N0, so
()
where Aspeed = 2/N0 ≈ 0.2 is a constant speedup parameter. The quantities and R are computed as the crystal grows.
In practice we have found that this relation yields growth rates that are somewhat too fast when R < N0Δr, owing to finite pixel size effects. We counter this by replacing R in (22) with
()
where we set R0 = N0Δr. This results in an improvement in the accuracy of the growth for small crystals with only a modest increase in running time.
The choice of Λ essentially means using an adaptive time step, where the physical time for each step equals
()
()

In running this code, we typically use Δτ = 1/2 and Δξ = 1, which gives Δr = X0. We define the radial index from i = 1 to N and the radius of the center of each spherical shell is ri = (i − 1)Δr.

3.3. Analytic Solutions

If the outer boundary is at infinity, the spherical growth case gives the analytic solution
()
where R is the radius of the sphere and αdiff = X0/R. In the limit α ≪ αdiff, we have σ(r) ≈ σ∞, while α ≫ αdiff gives σ(R) ≈ 0. The growth velocity in all cases is
()
With an outer boundary at rout and σ(rout) = σout, we have
()
where
()
and the growth velocity becomes
()
In computing vn, we may have to solve the equation
()
when γ is itself a function of σ(R). We solve this by iteration, using
()
at each time step, which quickly converges to σ(R).

3.4. Model Validation

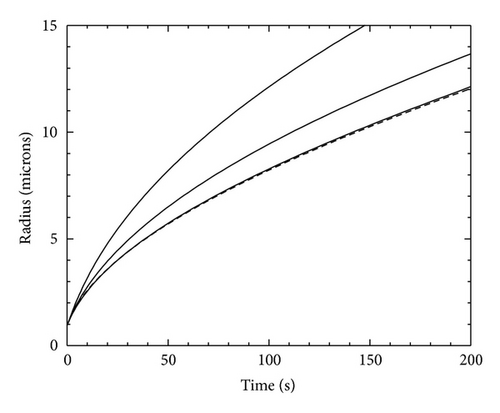
As an example that compares the model growth of a sphere with the analytic result, we use Δτ = 1/2, Δξ = 1, T = −15 °C, N = 300 (giving rout = 43.5 μm), σout = 0.01,   α = 1, and Rinitial = 6.5X0 = 0.94 μm. Results are shown in Figure 1 using different values of Aspeed. For the model with Aspeed = 1, the adaptive time steps were large, so σsurf did not have time to relax fully to its analytic value as the crystal grew, with the outcome that the crystal grew too fast. With smaller Aspeed values, the supersaturation field relaxed more fully and R(t) was closer to the analytic result.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
A comparison of different models for the growth of a spherical crystal (solid lines), together with the analytic result (dashed line), as described in the text. The models used Aspeed = 1 (top curve), 0.2 (middle), and 0.02 (lower).

3.5. Quantitative Comparisons with Experimental Data

In our experiments measuring ice growth rates, the outer boundaries of the growth chamber are much larger than typical crystal sizes, so rout ≈ ∞. In modeling such data, we require a certain modeling accuracy, and the straightforward route to achieving this is to run the code with some suitably small Aspeed together with some suitably large rout. Unfortunately the code converges rather slowly to analytic results, as seen in the example in Figure 1, and we have found that this straightforward approach results in unnecessarily long run times.

We have found an alternative operating strategy that achieves good modeling accuracy with substantially shorter run times. In this strategy we select values of rout that are not especially large and values of Aspeed that are not especially small and then adjust σout down to compensate. This strategy sacrifices model accuracy in exchange for increased modeling speed and is thus a variant of the usual trade-off one encounters in numerical modeling.

Figure 2 shows an example of how this modeling strategy can be used. The analytic curve uses the same parameters as in Figure 1, except with rout = ∞. The models also use the same parameters as in Figure 1, again with rout = 43.5 μm, and we fixed Aspeed = 0.2. The model with σout = 0.01 does not match the analytic curve, which reflects systematic errors in the numerical modeling. The model growth is faster than the analytic result because rout is too small and Aspeed is too large. We compensate for these systematic errors by adjusting σout downward 30 percent to 0.007, as seen in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Another comparison of different models for the growth of a spherical crystal (solid lines) with the analytic result (dashed line). The analytic calculation used σ∞ = 0.01 and rout = ∞. The models used Aspeed = 0.2 and rout = 43.5 μm, with σout = 0.01 (top curve), 0.007 (middle), and 0.004 (lower). This shows that one can adjust σout in the model to approximately compensate for systematic modeling errors.

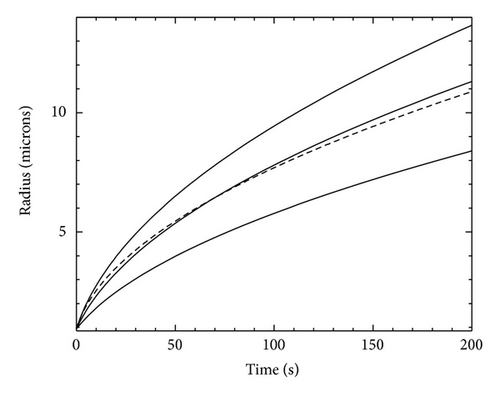
From this exercise we see that there are two ways to produce accurate models for comparison with experimental data. The first way is simply to use a large rout and a small Aspeed to reduce the modeling systematic errors to an acceptable level. This method is the most straightforward, but from a general perspective it is not the most efficient. The second approach is to use smaller rout and larger Aspeed, so the code runs quickly and then lowers σout slightly to compensate. This latter approach has proven quite useful in practice, especially when comparing experiments where σ∞ is itself not known with extremely high accuracy, as is often the case.

4. The 2D Cylindrically Symmetric Model

The 1D spherical model outlined above is useful for examining the cellular automata method in detail, but of course it is of little use otherwise, as analytic results can be computed for the general spherical case. Adding one additional dimension adds significant complexity and richness to the diffusion problem; however, analytic results are not possible for calculating the growth of even rather simple 2D morphologies.

We have found that a 2D cylindrically symmetric model is especially useful for comparison with ice crystal growth experiments. In this case a simple hexagonal plate is approximated by a circular disk, while a hexagonal column becomes a cylinder. The six prism facets are replaced by a single cylindrical “facet,” analogous to the spherical case above, and we equate the attachment kinetics on this surface to the attachment kinetics on a flat prism facet. Other than introducing a small geometrical correction, the cylindrical approximation appears to give reasonable quantitative results. It can be applied only to simple morphologies, such as simple plates and columns, hollow columns, and capped columns. Fortunately, experiments tend to focus on these simple morphologies, as they are best suited for examining surface growth dynamics.

The 2D diffusion equation in cylindrical coordinates is
()
for σ(r, z, t), giving the propagation equation
()
where τ is given in (7).
Including boundary conditions at the crystal surface follows along the lines of the 1D calculation above. Assuming Δτ = 1/4 and Δr = Δz gives the propagation equations for r-type and z-type boundary pixels
()
where
()
Note that a corner boundary pixel, with neighboring ice pixels in both r and z, will propagate using
()
which drains the supersaturation twice as fast as an ordinary boundary pixel as expected.
We then define an accumulated mass parameter λ, where λ starts at zero and after each timestep becomes
()
where the sum is over the number of neighboring ice pixels, and
()

4.1. The r  =  0 and z  =  0 Special Cases

In our model, we define the first row of pixels to have r = 0, which leads to problems with the (1 ± Δr/2r) factors. Going back to the diffusion equation, we use Gauss’s law to generate the propagation equation for r = 0 pixels
()
Unfortunately, taking Δτ = 1/4 in this expression leads to on-axis propagation instabilities. As a compromise between running speed and computational accuracy, we use Δτ = 1/6 for the on-axis propagation equation, giving
()
while we continue using Δτ = 1/4 for off-axis pixels. This causes the supersaturation field to relax slightly more slowly on the r-axis, but this fix apparently does not adversely affect the modeling results.
Similarly, we define the first row of z pixels to have z = 0, and for that row we use the propagation equation
()

4.2. Adaptive Time Steps

Speeding up the code using adaptive time steps again proceeds along the lines of the 1D problem. We use
()
with
()
as above, and the physical time step is that given in (25).

4.3. Neighbor Relations

In all these expressions we must choose the attachment coefficient α with some care, as its value will depend on the number and orientation of neighboring solid pixels. We label a boundary pixel with (Nr, Nz), where Nr is the number of neighboring ice pixels in the r direction and Nz is the number of ice neighbors in the z direction. Both Nr and Nz can take values 0, 1, or 2, giving nine cases for (Nr, Nz). The cases are
  •  

     (0,0) : the pixel is an air pixel;

  •  

    (0,1): one ice neighbor in the z direction, so α =   αbasal, the physical value appropriate for a basal facet surface;

  •  

    (1,0): one ice neighbor in the r direction, so α = αprism for a prism facet surface;

  •  

    (1,1): a kink site, where the growth will not be nucleation limited, since the corner provides a source of molecular steps. We do not know a priori what value to use for α on this site, but assume a constant α = α11;

  •  

    (0,2), (1,2), (2,0), (2,1), and (2,2): these are all unusual cases where the growth will be fast, so we assume that α = 1.

We index these possibilities with a single number by computing a boundary parameter . We then have B = 0 for an air pixel, B = 1 for a basal facet, B = 2 for a prism facet, B = 3 for a (1,1) kink location, and B > 3 for all other cases.

If we consider the special case where α is equal to some constant value, independent of the orientation of the surface with respect to the crystal lattice, then the growth velocity should equal v = αvkinσ for all surfaces. For the basal or prism facet surfaces in this constant-α case, we take αbasal = αprism = α, while an analysis of the growth of a (11) surface shows that we must take if the above algorithm is to produce the correct growth velocity.

4.4. Limitations on Grid Size

As we pointed out in [26], there are physical limits to how coarse the computing grid can be made before instabilities appear or the growth deviates substantially from real growth. Taking Δξ > 1/α would cause σsolid to become negative, which causes some concern in that it may produce instabilities in the code. With this limitation, the grid spacing could not be larger than Δr = Δz = X0/α. For air at a pressure of one atmosphere and α ≈ 1, this gives the pixel size X0 ≈ 0.145 μm.

Physically, we can gain some insights into these limitations from dendrite growth theory [7]. We have X0 ≈ Rkin (the latter from (27) in [7]), and a growing dendrite has a tip radius
()
where s is the dimensionless solvability parameter, which is of order unity for ice crystal growth [7]. The stability of the code thus limits the grid spacing to be no greater than the tip radius of a growing dendritic structure. From this we see that the code can only function properly when the grid spacing is fine enough to allow the growth of physically realistic dendritic structures, the scale of which is given by solvability theory.

In practice we typically assume that Δr = Δz = X0 ≈ 0.145 μm when comparing models with ice growth data. A coarser grid would reduce run times, but at the risk of not reproducing physically relevant morphological behaviors. We have not yet explored in detail how different grid sizes affect the modeling behavior.

4.5. Scaling Behavior

If we run the code and produce some complex crystal shape, the interpretation of our result still contains an ambiguity. The crystal size is given in pixels, where Δr = Δz = ΔξX0 is the pixel size. The parameter Δξ was fixed in the code, but X0 depends on the diffusion constant D, which is not otherwise specified. Similarly, a single time step in the code corresponds to a physical time
()

Thus we see that the growth behavior at different air pressures (different D) is determined once we know the growth at a single pressure (provided that σ∞ is the same at the different pressures). If the air pressure is half an atmosphere, the growth morphology (however, complex) will be the same as at one atmosphere, except in the former case the crystal will be double the size in double the time. This scaling behavior nicely explains why ice crystal morphology is generally simpler for smaller crystals and/or for lower air pressures, which has long been observed [7].

4.6. Analytic Solutions and Model Validation

The case of an infinitely long cylinder of radius Rin has the analytic solution
()
where the outer boundary has σ(Rout) = σRout and β = X0/Rinα, giving the growth velocity
()
with B = log (Rout/Rin).

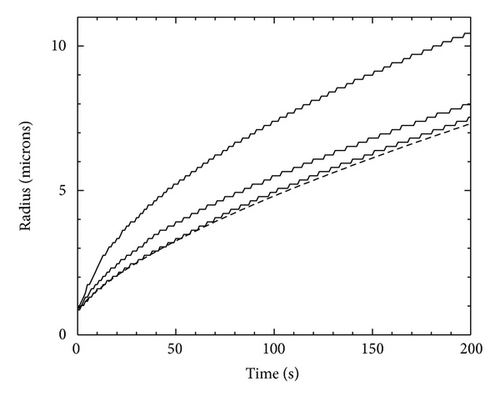
To compare this analytic result with numerical models of a growing cylinder, we created a version of our code with periodic boundary conditions in z, thus modeling the growth of an infinite cylinder. Figure 3 shows results using T = −15°C, σRout = 0.01,   Rinit = 1 μm, α = 1,Rout = 300, and X0 = 43.5 μm. Again we see that the numerical model converges to the analytic result as Aspeed goes to zero.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The dashed line shows the analytic result for the growth of an infinite cylinder with α = 1, Rout = 43.5 μm, and σRout = 0.01, as described in the text. Solid lines show numerical modeling results using Aspeed = 0.2 (top line), 0.02 (middle line), and 0.002 (bottom line).

5. Gibbs-Thomson Effect

The basic cellular automata code described above includes a fairly realistic treatment of the attachment kinetics but does not include any effects of surface energy. This is somewhat justified for the case of faceted ice crystal growth as one can show that attachment kinetic effects dominate the growth behavior, while surface energy effects are less important [7]. Nevertheless, surface energy effects are not always negligible, especially at low supersaturations. As we will demonstrate below, models with highly anisotropic attachment kinetics and no surface energy effects can exhibit the formation of one-pixel-wide features that are not physically plausible. To suppress these unphysical models we must include the surface energy via the Gibbs-Thomson effect.

For the ice case we are considering here, the equilibrium vapor density above a curved surface can be written [27]:
()
where csat  is the equilibrium (saturated) vapor density of a flat surface, κ is the surface curvature
()
where r1, r2 are the principal radii of curvature of the surface, and
()
where γ ≈ 0.1 J/m2 is the surface energy of the ice/vapor interface. The anisotropy of γ is not well known, but the available evidence suggests it is rather small [20], so for the remainder of our discussion, we assume an isotropic surface energy. We believe this is a accurate assumption for ice, but it is in stark contrast to the highly anisotropic ice surface energy assumed in [11].
From this we have the supersaturation over a curved surface
()
to lowest order in δ/Rc,  where σ is the normal supersaturation relative to a flat interface, and for later convenience we define Rc = κ−1. Putting in some numbers, a sharp ice needle might have Rc ≈ 1 μm, giving Δσ = σcurved − σ ≈ 0.1 percent, which is small but not always negligible. Moreover, setting Rc ≈ X0 ≈ 0.15 μm gives a rather large Δσ ≈ 0.66 percent, indicating that one-pixel-wide features should not be present at low supersaturations.

Adding the Gibbs-Thomson effect requires an algorithmic estimation of Rc for all boundary pixels in our cellular automata model. We examined several possibilities but did not find a suitable algorithm that could be used with arbitrary morphologies in our cylindrically symmetrical model. Since our primary goal was to model simple morphologies for comparison with experimental data, as described above, we settled for a simpler algorithm for such cases.

Throughout our investigations, we found that the overall growth behavior of faceted crystals with simple morphologies was determined primarily by the growth of the outermost facet surfaces. To apply the Gibbs-Thomson effect on these surfaces, we defined the outer boundary pixels as shown in Figure 4, yielding the numbers Nr and Nz as the number of outer-boundary pixels.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
A graphical definition of the outer boundary pixels used for incorporating surface energy effects into our cellular automata model. Here the blue pixels are ice, while the clear pixels are air. The red pixels are boundary pixels having the largest r and z values, defined to be the “outer” boundary pixels.

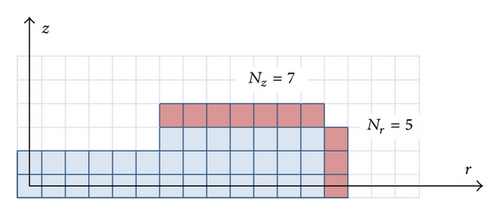
Using these outer boundary pixels as a proxy for estimating surface curvature, we defined Rc = ΔrNr/2 for the edges of plates, Rc = ΔrNz/2 for the edges of hollow columns and Rc = ΔrNz/4 for the tips of needles. For all boundary pixels that were not outer-boundary pixels, we assumed that Rc = ∞. Although these are crude estimations of surface curvature, we found them satisfactory for incorporating the Gibbs-Thomson effect in our model, in part because this is a relatively small effect compared to the more dominant role of attachment kinetics.

5.1. A Gibbs-Thomson Example

The top image in Figure 5 shows how our model can yield unphysical results if we do not include the Gibbs-Thomson effect. In this model we assumed the input parameters: T = −15°C, σ∞ = 0.01,   αbasal = exp (−0.03/σsurf), αprism = 1, an initial prism radius R0 = 2 μm, initial prism half-height H0 = 5 μm, and a Gibbs-Thomson parameter δ = 0. After growing this model for six seconds, the initial simple prism grew into a capped column where the two capping plates each had a thickness of just one pixel, as shown in the top image in Figure 5. Such small structural features are unphysical at this supersaturation, and similar one-pixel-wide features often appeared in our models when the supersaturation was low and the anisotropy in attachment kinetics was high.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
A test of the Gibbs-Thomson effect in our crystal growth model. In each image the white pixels show ice, while the brightness of the surrounding region is proportional to the supersaturation. Model crystals are reflection symmetric about the z = 0 plane, and the images show z ≥ 0 only. Thin vertical lines show the initial crystal size. Using αprism = 1 and αbasal ≪ αprism resulted in growth only on the prism surfaces. Full model parameters are given in the text. The top image displays the crystal after six seconds of growth with a Gibbs-Thomson parameter δ = 0. This model exhibits a one-pixel-thick plate growing on the end of the column, which is not physically plausible. The middle and lower images show results using δ = 0.3 and 1.0 nm, respectively. For these models the unphysical plate growth does not appear.

Including nonzero values of δ suppressed these small features, as demonstrated in the lower two images in Figure 5. From this example, as well as additional tests with different growth morphologies, we found that our relatively simple algorithm for including the Gibbs-Thomson effect yielded reasonable results, suppressing the unphysical growth of one-pixel-wide features. Models with higher σ∞ values or with lower anisotropies in the attachment kinetics were generally less affected by including the Gibbs-Thomson effect.

6. An Example Comparison with Experiment

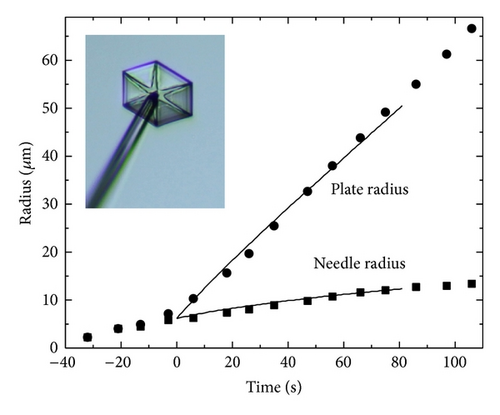
Figure 6 shows an example of how the cellular automata method can be used in laboratory investigations of growing ice crystals. In this experiment we first grew a thin “electric” ice needle, as described in [28], and then transferred the needle to a second growth chamber where we grew a thin plate-like crystal on the needle tip, all in air at a pressure of one bar. The hexagonal symmetry of the crystal and the relatively simple growth morphology were well suited for analysis using our cylindrically symmetric model. By adjusting σ∞ and the surface attachment coefficients for the principal facets, we were able to generate a model crystal that matched both the morphology and growth rates of the laboratory crystal. In addition to the plate and needle radii, note that the tapered neck of the needle just below the plate, seen in Figure 6, was nicely reproduced by the model crystal. A discussion of the physical significance of the best-fit model parameters used for this model is left for a subsequent publication, comparing the growth of many crystals under different conditions. This example is meant to demonstrate only that the behavior of faceted laboratory-grown ice crystals can be accurately modeled with the cellular automata method.

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
An example showing our numerical modeling of a laboratory-grown ice crystal. The composite image in (a) shows five successive views of a thin plate-like crystal growing on the end of a slender ice needle, with a 50 μm scale bar. The crystal is shown in a side view, with illumination from behind. The composite image in (b) shows our numerical model of the same crystal. Here the brightness around the crystal is proportional to supersaturation. The data points in (c) shows measurements of the plate and needle radii (the latter at a distance of 50 μm from the base of the plate) as a function of time. The lines in the graph are from the growth of the model crystal. The inset image in (c) shows a more frontal view of a similar plate-on-needle crystal with a plate radius of 80 μm, showing the thin sectored-plate morphology. Note that at earlier times (t < 0 in the graph) the crystal was growing from a tapered needle to a column with nearly uniform radius along its length. The time axes were shifted, so the plate began growing at t ≈ 0 for both the real and model crystals.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
An example showing our numerical modeling of a laboratory-grown ice crystal. The composite image in (a) shows five successive views of a thin plate-like crystal growing on the end of a slender ice needle, with a 50 μm scale bar. The crystal is shown in a side view, with illumination from behind. The composite image in (b) shows our numerical model of the same crystal. Here the brightness around the crystal is proportional to supersaturation. The data points in (c) shows measurements of the plate and needle radii (the latter at a distance of 50 μm from the base of the plate) as a function of time. The lines in the graph are from the growth of the model crystal. The inset image in (c) shows a more frontal view of a similar plate-on-needle crystal with a plate radius of 80 μm, showing the thin sectored-plate morphology. Note that at earlier times (t < 0 in the graph) the crystal was growing from a tapered needle to a column with nearly uniform radius along its length. The time axes were shifted, so the plate began growing at t ≈ 0 for both the real and model crystals.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
An example showing our numerical modeling of a laboratory-grown ice crystal. The composite image in (a) shows five successive views of a thin plate-like crystal growing on the end of a slender ice needle, with a 50 μm scale bar. The crystal is shown in a side view, with illumination from behind. The composite image in (b) shows our numerical model of the same crystal. Here the brightness around the crystal is proportional to supersaturation. The data points in (c) shows measurements of the plate and needle radii (the latter at a distance of 50 μm from the base of the plate) as a function of time. The lines in the graph are from the growth of the model crystal. The inset image in (c) shows a more frontal view of a similar plate-on-needle crystal with a plate radius of 80 μm, showing the thin sectored-plate morphology. Note that at earlier times (t < 0 in the graph) the crystal was growing from a tapered needle to a column with nearly uniform radius along its length. The time axes were shifted, so the plate began growing at t ≈ 0 for both the real and model crystals.

7. Discussion

Numerical modeling of structure formation during solidification has been well studied for decades, especially cases where weak surface anisotropies in diffusion-limited growth yield rounded dendritic branching. Modeling structures that are both branched and faceted have been more difficult, and only recently researchers have demonstrated suitable numerical methods [10, 11]. In the present work we have developed a numerical model aimed at investigating the formation of simple faceted morphologies during ice crystal growth. Our model incorporates the cellular automata technique in [10] but uses a more physically realistic treatment of the surface attachment kinetics and the Gibbs-Thomson effect. Using this model, we are able to reproduce ice crystal growth behavior for simple growth morphologies over a broad range of conditions. We have been using this model to aid in the interpretation of ice growth experiments, in order to extract information about the anisotropic surface attachment kinetics that governs ice crystal growth from water vapor. Modifying the model for application to other material systems is likely straightforward.

At present we have limited our model to cylindrically symmetric crystal growth and relatively simple growth morphologies, for comparison with measurements. A full three-dimensional extension of our model should be possible, as was demonstrated in [10], potentially allowing complete modeling of the many complex branched and faceted structures that are commonly observed in ice crystal growth [7]. Achieving this goal would likely require a substantially better understanding of the surface attachment kinetics in ice than presently exists, along with more advanced algorithms for incorporating all the relevant surface physics into a cellular automata model.

In general, it appears that the cellular automata method is well suited for modeling faceted crystal growth, and it may be the method of choice in material systems exhibiting strongly anisotropic attachment kinetics. Incorporating more sophisticated descriptions of surface growth processes will require substantially better algorithms than we have outlined above, especially when extending the models to three dimensions. Whether such models can reproduce the full range of complex structures appearing in faceted crystal growth remains to be seen.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.