Advances in Materials Science and Engineering
Volume 2013, Issue 1 167823
Research Article
Open Access

Scaling Analysis of the Tensile Strength of Bamboo Fibers Using Weibull Statistics

Jiaxing Shao, 

Jiaxing Shao

School of Materials Science and Engineering, Southwest University, Chongqing 400715, China southwest.edu

Faculty of Materials and Energy, Southwest University, Chongqing 400715, China shu.edu.cn

Search for more papers by this author
Fang Wang, 

Corresponding Author

Fang Wang

School of Materials Science and Engineering, Southwest University, Chongqing 400715, China southwest.edu

Faculty of Materials and Energy, Southwest University, Chongqing 400715, China shu.edu.cn

Search for more papers by this author
Lu Li, 

Lu Li

School of Materials Science and Engineering, Southwest University, Chongqing 400715, China southwest.edu

Faculty of Materials and Energy, Southwest University, Chongqing 400715, China shu.edu.cn

Search for more papers by this author
Junqian Zhang, 

Junqian Zhang

Department of Mechanics, Shanghai Key Laboratory of Mechanics in Energy and Environment Engineering, Shanghai University, Shanghai 200444, China shu.edu.cn

Search for more papers by this author
First published: 29 October 2013
https://doi.org/10.1155/2013/167823
Citations: 13
Academic Editor: Xing Chen

Abstract

This study demonstrates the effect of weak-link scaling on the tensile strength of bamboo fibers. The proposed model considers the random nature of fiber strength, which is reflected by using a two-parameter Weibull distribution function. Tension tests were performed on samples that could be scaled in length. The size effects in fiber length on the strength were analyzed based on Weibull statistics. The results verify the use of Weibull parameters from specimen testing for predicting the strength distributions of fibers of longer gauge lengths.

1. Introduction

In recent decades, natural fiber reinforcement has gained much attention as realistic, environmental-friendly alternatives to synthetic fibers. As typical biological materials with unique multiscale structures, natural fibers approximate or even exceed the specific mechanical properties of man-made fibers [1]. Among many natural fibers used as composite materials, bamboo fiber is one that offers the most potential because of its low density, low cost, high specific strength, and stiffness [2]. Understanding the mechanical properties of bamboo fiber is necessary for ensuring the reliability of such materials for designing proper composite structures.

Fibers are the main load-bearing elements of a fiber-reinforced composite, which means that most of the mechanical properties of fiber-reinforced composites are primarily affected by fiber strength distribution [3] and gauge length dependence [4]. The properties of bamboo fibers depend on growing condition, including growth duration and procedures involved in extracting the fiber from the plant [5]. In addition, bamboo fibers are typically brittle [6]. The strength of brittle materials and the effect of size have drawn the attention of scientists and technologists [7–11]. The statistical weakest link theory, which was formulated based on conventional brittle fracture study, is based on the assumption that a material can be divided into smaller elements that are linked together, with the fracture beginning in the weakest link, and failure occurs when any of the links fail [12]. Considering that fiber strength is not constant even with uniform length and diameter, the statistical strength of fibers depends on the distribution of defects within the fiber. Although many studies have tried to predict fiber strength [5, 10, 13], very few statistical strength models have tried to describe the failure behavior of bamboo fibers. Therefore, we need an efficient method for evaluating bamboo strength for design and manufacturing.

The aim of the present paper is to investigate the scaling effects involved in predicting the ultimate tensile strength of bamboo fibers. Tension tests were performed to describe the statistical strength distributions of bamboo fibers. The measured fiber strengths at different gauge lengths were analyzed according to a two-parameter Weibull distribution. Thus, we established a method for determining statistical parameters used for characterizing strength distribution. Fibers 20, 30, 40, 50, and 60 mm long were used to investigate the dependence of strength on fiber size. The accuracy of using weak-link scaling statistics for fiber strength was also examined.

2. Experimental Procedure

The bamboo fibers were produced by Ban Ltd., Tokushima, Japan. The scanning electron micrograph of the longitudinal section of a bamboo fiber measured in the present study is shown in Figure 1. Bamboo fibers were clearly composed of elementary fibers connected by constituents, such as considerable amounts of pectins [14]. Although the microstructural framework of bamboo fibers could be called “elementary bamboo fiber bundles,” it was treated as a single fiber during macroscale tensile deformation [15]. In the present study, fiber diameter ranged from 150 μm to 450 μm. To study size effects on fiber length, the samples used in all tests had the same diameters, approximately 200 ± 15 μm.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Longitudinal photomicrographs of bamboo fiber.

To fix the fiber as straight as possible between the clamps, a fiber specimen is mounted on a paper frame that matches the gauge length chosen for the test. The ends of the fiber were glued to the tab using a double-sided adhesive. The frame was cut after clamping in the jaws of the testing machine. The opening of the paper frame determined the gauge length. For this experiment, the gauge lengths were set to 20, 30, 40, 50, and 60 mm. Fifty individual fibers were tested at each of the five gauge lengths. Fiber length was measured to an accuracy of ±1 mm at each end. Tests were performed on a variety of lengths to investigate the effects of fiber length on tensile strength. To prevent additional flaws caused by the clamping force, samples broken near the edge of the clamps were excluded from the analysis.

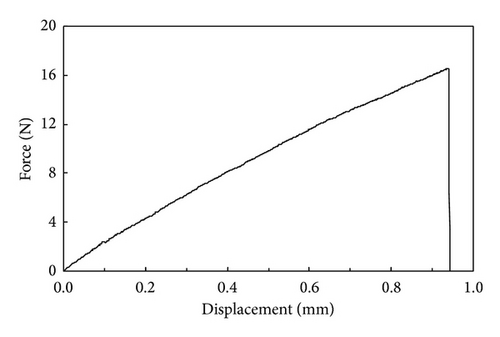
Fiber specimens were mechanically tested on a WDW3050 computer-controlled universal testing machine. All static tests were conducted in displacement control mode at a rate of 0.5 mm/min and at ambient temperature under atmospheric pressure. All samples were maintained under load until mechanical failure occurred, with failure being defined as the point in which the laminate no longer supported the externally applied load. The forces applied and the testing machine displacements were directly recorded by an acquisition system and on a chart recorder. Therefore, tensile strength was taken as the ratio of the maximum load applied to the cross-sectional area of the specimen. Based on a typical load-displacement response shown in Figure 2, the tensile load increased proportionally with increasing strain until the point of ultimate load, which is the point at which the bamboo fibers broke and exhibited brittle fractures with no apparent yielding.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The experimental results of a classical load-displacement curve of bamboo fiber.

3. Weibull Statistics

Brittle fibers typically exhibit wide variability in strength, which is determined by the microstructural flaws that act as stress concentrations. These internal defects occur randomly along the length of the fiber. Fracture stresses measured on specimens with identical dimensions have a statistical distribution because of the widely varying severity of flaws caused by variability in shape, size, and location with respect to stress state [11]. Weibull statistical analysis is the best candidate for characterizing variations in fiber strength [8, 16]. Fiber strength, σf, is a stochastic variable that can be described by a two-parameter Weibull cumulative distribution function P(σf):
()
where P, in the range of [0,  1], is the failure probability of single fibers under an applied stress less than or equal to σf. σ0 is the Weibull scale parameter or characteristic stress for a reference length L0. β is the Weibull modulus or shape parameter, which describes the variability of the failure strengths. The common values for β of pristine fibers range from 2 to 20 [3].
Since σf follows a Weibull distribution, the probability density function (PDF) of σf is obtained from (1), which is
()
Figure 3 presents the effect of scale parameter β on the shape of the probability density function when σ0 = 600 MPa. This finding indicates that β variations significantly affect the distribution of fiber tensile strength; that is, smaller β values indicate larger spreads in fiber strength and vice versa. A peak of probability density function is observed when σf is equal to σ0. The parameters β and σ0 can be calculated statistically as follows:
()
where E(σf) and D(σf) are the mean and variance of random variable, respectively. Γ is the gamma function.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Weibull distribution of fiber strength.
Expressing (1) in a linear form would facilitate using the equation to describe the experimental data. Rearranging and taking logarithms twice resulted in the following equation:
()

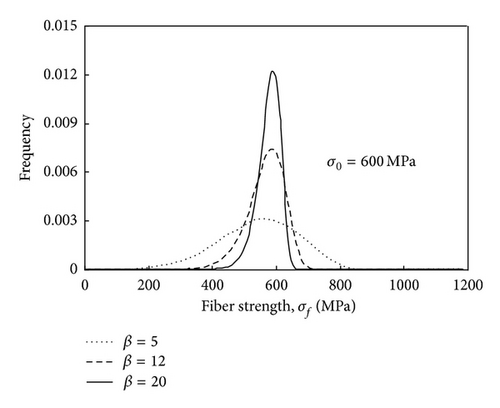
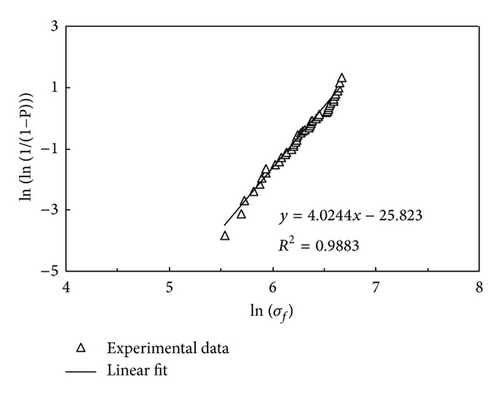
Hence, a plot of ln (σf) versus ln (ln (1/(1 − P))) should give a straight line if the material strength variability is described by the Weibull distribution. The shape parameter β and the scale parameter σ0 can both be obtained from the slope and y-intercept of this line, respectively.

P can be calculated using a statistical approximation technique. N samples of σf are ranked in an ascending order, σfi,   i = 1 −  N. σfi is denoted by the ith strength value (i = 1 corresponds to the smallest and i = n corresponds to the highest strength value). Then, the ith value is computed as follows:
()

4. Weak-Link Scaling

Weak-link theory, which accurately describes the failure of many brittle materials, is based on the assumption that the material can be divided into smaller linked elements and that the fracture of a specimen is identified with the unstable propagation of the most “critical” crack [12].

Based on the weakest link theory, Weibull [8] proposed a strength σf distribution
()
where P is the failure probability of a long fiber that is connected by n independent segments and V is the tested volume. V0 is the volume of a unit link or segment, which is a scaling constant [17].
If the diameter,  D, of all fibers is assumed to be the same, (6) can be written as
()
where L0 is the reference length and L is the fiber gauge length.
From (7), the average strength is a power function of gauge length L [18],
()

If the strength of a material is determined by weak-link statistics, longer fibers have a larger number of links than shorter fibers and have a higher probability of encountering a more severe flaw along the fiber [19]. Furthermore, longer fibers have lower average fracture strengths than shorter fibers. In other words, the strength of the materials decreases with increasing size [9]. Therefore, weak-link scaling predictions assume that the strength can be scaled for any fiber length, from a single weak-link point estimate at a chosen fiber gauge length [13].

Considering (7) for the same probability of failure for two specimens with identical stress distributions, the strength values obtained at any given gauge length can be scaled to predict the strength of another length of fiber and for a similar probability of failure as follows:
()
where σ2 and σ1 are the fiber strengths at gauge lengths L2 and L1, respectively. This equation directly links strength to volume; therefore, this equation quantifies the size effect, which is the basis for the statistical weakest link model.
The work by Curtin [20] indicated that a large system could be formally considered to be composed of a collection of independent subsystems linked in series, so that failure in the weakest subsystem causes failure across the entire system. Therefore, the cumulative probability of failure of a fiber with volume V2 loaded with stress σf is related to the cumulative probability of failure of a  fiber with volume V1 as follows:
()
With constant fiber diameter, (10) becomes
()

5. Results and Discussion

5.1. Statistical Distribution of Tensile Strength

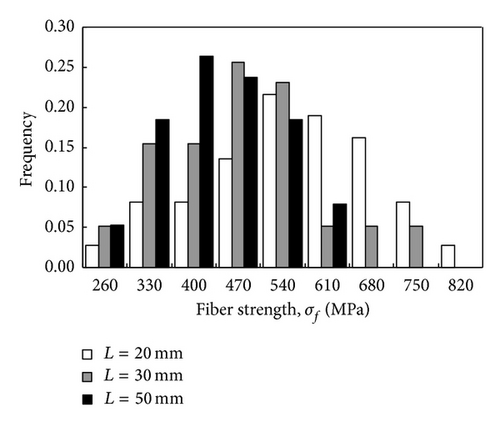
Figure 4 shows the histogram of the tensile strength distribution under three fiber lengths (L = 20, 30, and 50 mm). Tensile strength is clearly not homogeneous. Ultimate strength is more scattered in shorter fibers than in longer fibers. Therefore, the mean decreases with increased scattering of fiber tensile strength [21].

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The experimental probability density function for ultimate strength of bamboo fiber.
A typical Weibull plot of bamboo fracture strength at 20 mm gauge length based on (1) is shown in Figure 5. The linear relationship of X = ln (σf) versus Y = ln (ln (1/(1 − P))) determined using the least squares method is shown in Figure 5. The R2 coefficient is 0.9883, which indicates a good degree of linearity. From this plot, the statistical parameters of the Weibull distribution can be obtained as listed
()
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Strength distributions of bamboo fibers with L = 20 mm.

5.2. Effect of Specimen Length on Ultimate Strength

The relationship between the mean tensile strength of bamboo fiber and the testing gauge length is plotted on Figure 6. Fifty filaments are measured for each data point. The finding shows that the tensile strength depends on the specimen length of the fibers. A decrease in tensile strength was observed with increasing test length, which is attributed to the increasing probability of encountering more severe flaws with larger test lengths. Hence, longer fibers should on average have lower strengths than shorter fibers.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Length dependence of the mean tensile strength of bamboo fibers.

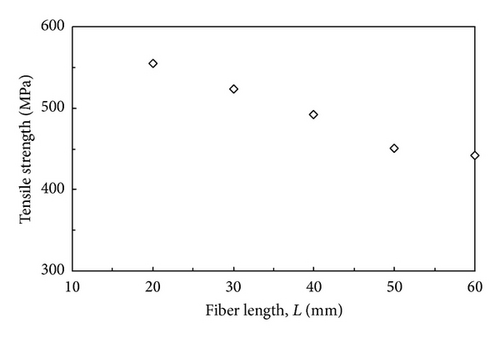
If the characteristic strength at a given gauge length is known, the mean strength at other gauge lengths can be calculated based on (8). In Table 1, the tensile strengths predicted through size scaling from L = 20 mm are presented as a function of fiber test length; these findings are in excellent agreement with the experimental measurements. The Weibull theory clearly accounted for the correlation of strength variations with size [22].

Table 1. Comparison of measured and predicted fracture strengths of bamboo fibers.
Fiber test length (mm) Tensile strength Difference (%)
Measured by experiment* (MPa) Predicted by (8) (MPa)
20 555 — —
30 523 502 4.26
40 492 467 5.35
50 451 442 2.12
60 442 422 4.60
  •  *Average value of 50 results.

5.3. Strength Prediction by Weak-Link Scaling

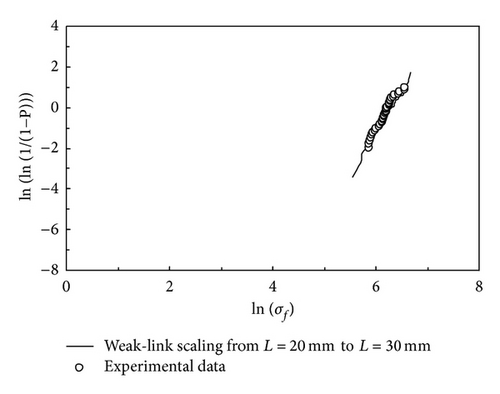
Predictions of the tensile strengths were made by size scaling data from samples of longer gauge lengths to access the accuracy of weak-link scaling. An example comparing the experimental and predicted bamboo strength distribution for L = 30 mm is presented in Figure 7. The distribution of open circles is the experimental result for fiber length of L = 30 mm. The solid line represents the L = 20 mm (fiber gauge length) distribution weak link scaled to L = 30 mm (fiber gauge length) using (11). The results show that weak-link scaling works well, except at the lowest or highest fiber strengths. This exception is due to greater distributed damage in L =  20 mm fibers than in L = 30 mm fibers. The studies in the literature [16, 20] show that a critical damage size is necessary for weak-link scaling, which is the subject of our future study.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Strength distributions for bamboo fibers with L = 30 mm.

6. Conclusions

The tensile strength distribution of fibers is a key constitutive property of fiber-reinforced composites. Thus, understanding the scaling effects in the tensile properties of natural fibers is important. In the present study, bamboo fibers were tested with tension at several different gauge lengths. For each gauge length, 50 individual fibers were measured. The experimental fiber strength values were compared with the predicted values through weak-link scaling. The following conclusions were drawn.
  • (1)

    Tensile strength of bamboo fibers exhibits statistical Weibull-type distribution, which is not necessarily constant. The two statistical parameters, β and σ0, were used to quantify the variations in strength, which can be readily determined from static tensile tests on several fibers at a given gauge length L0.

  • (2)

    Ultimate fiber strength depends on specimen length, which is dominated by flaws statistics. This dependence is due to the increased probability of flaws that cause failure with larger material volumes. The gauge length effect on bamboo fiber strength can be predicted through weak-link scaling.

  • (3)

    The simulated cumulative failure probability from the scaling model is consistent with the test data. These results verify the use of Weibull parameters from specimen testing for predicting the strength distributions of fibers of longer gauge lengths.

Acknowledgments

The authors gratefully acknowledge the financial support of National Science Foundation of China under Grant no. 11102169, National Science Foundation Project of CQ CSTC under Grant no. 2012JJA70002, and Fundamental Research Funds for the Central Universities under Grant nos. XDJK2013B019, XDJK2013D011.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.