Abstract and Applied Analysis
Volume 2013, Issue 1 167065
Research Article
Open Access

Delayed Feedback Control and Bifurcation Analysis of an Autonomy System

Zhen Wang, 

Corresponding Author

Zhen Wang

Institute of Information and System Computation Science, Beifang University of Nationalities, Yinchuan, Ningxia 750021, China

Search for more papers by this author
Huitao Zhao, 

Huitao Zhao

Department of Mathematics and Information Science, Zhoukou Normal University, Zhoukou, Henan 466001, China zknu.edu.cn

Department of Applied Mathematics, Kunming University of Science and Technology, Kunming, Yunnan 650093, China kmust.edu.cn

Search for more papers by this author
Xiangyu Kong, 

Xiangyu Kong

Institute of Information and System Computation Science, Beifang University of Nationalities, Yinchuan, Ningxia 750021, China

Search for more papers by this author
First published: 24 April 2013
https://doi.org/10.1155/2013/167065
Citations: 1
Academic Editor: Yisheng Song

Abstract

An autonomy system with time-delayed feedback is studied by using the theory of functional differential equation and Hassard’s method; the conditions on which zero equilibrium exists and Hopf bifurcation occurs are given, the qualities of the Hopf bifurcation are also studied. Finally, several numerical simulations are given; which indicate that when the delay passes through certain critical values, chaotic oscillation is converted into a stable state or a stable periodic orbit.

1. Introduction

Since the first chaotic attractor was found by Lorsenz in 1963, the theory of chaos has been developing rapidly. The topics of chaos and chaotic control are growing rapidly in many different fields such as biological systems and ecological and chemical systems [1–5]. The desirability of chaos depends on the particular application. Therefore, it is important that the chaotic response of a system can be controlled.

Many researchers have proposed chaos control and synchronization schemes in recent years [6–11]; among which, delayed feedback controller (DFC) is an effective method for chaos control; it has been receiving considerable attention recently [11–14]. The basic idea of DFC is to realize a continuous control for a dynamical system by applying a feedback signal which is proportional to the difference between the dynamical variable X(t) and its delayed value [14]. Choosing the appropriate feedback strength and time delay can make the system stable. The delayed feedback control method does not require any computer analysis and can be simply implemented in various experiments. For example, Song and Wei in [15] investigated the chaos phenomena of Chen’s system using the method of delayed feedback control. Their results show that when K taking some value, taking the delay τ as the bifurcation parameter when τ passes through a certain critical value, the stability of the equilibrium will be changed from unstable to stable, chaos vanishes and a periodic solution emerges.

Let us consider a system of nonlinear autonomous differential equations as follows:
()
When a = 0.2,  b = 0.02, the zero equilibrium of system (1) is unstable and system (1) is chaotic (see Figure 1). For control of chaos, we add a time-delayed force K(y(t) − y(t − τ)) to the second equation of system (1), that is, the following delayed feedback control system:
()
When K = 0 or τ = 0, we can see that system (2) is the same as system (1). In this paper, by taking τ as bifurcation parameter, we will show that when K takes some value, with the increasing of τ, the stability of zero equilibrium of system (2) will change, and a family of periodic orbits bifurcates from zero equilibrium.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (1) with a = 0.2 and b = 0.02.

This paper is organized as follows. In Section 2, we first focus on the stability and Hopf bifurcation of the zero equilibrium of system (2). In Section 3, we derive the direction and stability of Hopf bifurcation by using normal form and central manifold theory. Finally in Section 4, an example is given for showing the effects of chaotic control.

2. Local Stability and Delay-Induced Hopf Bifurcations

In this section, by analyzing the characteristic equation of the linearized system of system (2) at the equilibriums, we investigate the stability of the equilibriums and the existence of local Hopf bifurcations occurring at the equilibriums.

System (2) has two equilibriums, E0(0,0, 0) and E*(x*, y*, z*), where
()
The linearization of system (2) at E0 is
()
whose characteristic equation is
()
where a2 = 8 + b − a − K,  a1 = 8b − 8K − ab + aK − 8a + 1,  a0 = 8aK − 8ab − a + 8,  b2 = K,  b1 = (8 − a)K,  b0 = −8aK, and . Thus, we need to study the distribution of the roots of the third-degree exponential polynomial equation. For this end, we first introduce the following simple result which was proved by Ruan and Wei [16] using Rouche’s theorem.

Lemma 1. Consider the exponential polynomial

()
where τi ≥ 0  (i = 1,2, …, m) and are constants. As (τ1, τ2, …, τm) vary, the sum of the order of the zeros of on the open right half-plane can change only if a zero appears on or crosses the imaginary axis.

Obviously, iω  (ω > 0) is a root of (5) if and only if ω satisfies
()
Separating the real and imaginary parts, we have
()
which is equivalent to
()
Let z = ω2, and then (9) becomes
()
where , and .
Denote
()
Then, we have the following lemma.

Lemma 2. For the polynomial equation (10), one has the following results.

  • (i)

    If r < 0, then (10) has at least one positive root.

  • (ii)

    If r ≥ 0 and ∆ = p2 − 3q ≤ 0, then (10) has no positive roots.

  • (iii)

    If r ≥ 0 and ∆ = p2 − 3q > 0, then (10) has positive roots if and only if and .

Suppose that (10) has positive roots, without loss of generality; we assume that it has three positive roots, defined by z1,  z2, and z3, respectively. Then (9) has three positive roots
()
Thus, we have
()
If we denote
()
then ±iωk is a pair of purely imaginary roots of (9) with . Define
()
Note that when τ = 0, (5) becomes
()
Therefore, applying Lemmas 1 and 2 to (5), we obtain the following lemma.

Lemma 3. For the third-degree transcendental equation (5), one has the following results.

  • (i)

    If r ≥ 0 and ∆ = p2 − 3q ⩽ 0, then all roots with positive real parts of (5) have the same sum to those of the polynomial equation (16) for all τ ≥ 0.

  • (ii)

    If either r < 0 or r ≥ 0 and , and , then all roots with positive real parts of (5) have the same sum to those of the polynomial equation (16) for τ ∈ [0, τ0).

Let λ(τ) = α(τ) + iω(τ) be the root of (9) near satisfying
()
Then it is easy to verify the following transversality condition.

Lemma 4. Suppose that and h′(zk) ≠ 0, where h(z) is defined by (15). Then , and and h′(zk) have the same sign.

Now, we study the characteristic equation (5) of system (4). Applying Lemmas 3 and 4 to (5), we have the following theorem.

Theorem 5. Let and ω0, τ0 be defined by (14) and (15), respectively. Then consider the following.

  • (i)

    If r ≥ 0 and ∆ = p2 − 3q ≤ 0, then all roots with positive real parts of (5) have the same sum to those of the polynomial equation (16) for all τ ≥ 0.

  • (ii)

    If either r < 0 or r ≥ 0 and ∆ = p2 − 3q > 0,  , and , then h(z) has at least one positive root zk, and all roots with positive real parts of (5) have the same sum to those of the polynomial equation (16) for τ ∈ [0, τ0).

  • (iii)

    If the conditions of (ii) are satisfied and h′(zk) ≠ 0, then system (2) exhibits Hopf bifurcation at the equilibrium E0 for .

3. Stability and Direction of Bifurcating Periodic Orbits

In the previous section, we obtain the conditions under which family periodic solutions bifurcate from the equilibrium E0 at the critical value of τ. As pointed by in Hassard et al. [17], it is interesting to determine the direction, stability, and period of these periodic solutions. Following the ideal of Hassard et al., we derive the explicit formulae for determining the properties of the Hopf bifurcation at the critical value of τ using the normal form and the center manifold theory. Throughout this section, we always assume that system (2) undergoes Hopf bifurcations at the equilibrium E0 for τ = τk, and then ±iωk is corresponding to purely imaginary roots of the characteristic equation at the equilibrium E0.

Letting τ = τt,   τ = τk + μ, system (2) is transformed into an FDE in C = C([−1,0], R3) as
()
where u(t) = (x(t), y(t), z(t)) T ∈ R3 and Lμ : C → R,   f : R × C → R are given, respectively, by
()
()
By the Riesz representation theorem, there exists a function η(θ, μ) of bounded variation for θ ∈ [−1,0], such that
()
In fact, we can choose
()
where δ is Dirac-delta function.
For ϕ ∈ C1([−1,0], R3), define
()
Then, when θ = 0, system (18) is equivalent to
()
where ut(θ) = u(t + θ) for θ ∈ [−1,0]. For ψ ∈ C1([0,1], (R3) *), define
()
and a bilinear inner product
()
where η(θ) = η(θ, 0). Then A = A(0) and A* are adjoint operators. By the discussion in Section 2, we know that ±iωkτk are eigenvalues of A. Thus, they are also eigenvalues of A*. We first need to compute the eigenvector of A and A* corresponding to iωkτk and −iωkτk, respectively. Suppose that is the eigenvector of A corresponding to iωkτk. Then Aq(θ) = iωkτkq(θ). It follows from the definition of A and (19), (21), and (22) that
()
Thus, we can easily get
()
Similarly, let be the eigenvector of A* corresponding to −iωkτk. By the definition of A* and (19), (21), and (22), we can compute
()
In order to assure 〈q*(s), q(θ)〉 = 1, we need to determine the value of D. From (26), we have
()
Thus, we can choose D as
()
In the following, we first compute the coordinates to describe the center manifold C0 at μ = 0. Let ut be the solution of (18) when μ = 0. Define
()
On the center manifold C0, we have
()
where z and are local coordinates for center manifold C0 in the direction of q and  q*. Note that W is real if ut is real. We consider only real solutions. For the solution ut ∈ C0 of (18), since μ = 0, we have
()
where
()
By (32), we have , and then
()
It follows together with (20) that
()
Comparing the coefficients with (35), we have
()
In order to determine g21, in the sequel, we need to compute W20(θ) and W11(θ). From (24) and (32), we have
()
where
()
Notice that near the origin on the center manifold C0, we have
()
Thus, we have
()
Since (39), for θ ∈ [−1,0), we have
()
Comparing the coefficients with (40) gives that
()
From (43), (46), and the definition of A, we can get
()
Noticing that , we have
()
where is a constant vector. In the same way, we can also obtain
()
where is also a constant vector.
In what follows, we will seek appropriate E1 and E2. From the definition of A and (42), we obtain
()
()
where η(θ) = η(0, θ). From (39) and (40), we have
()
()
Substituting (46) and (50) into (48) and noticing that
()
we obtain
()
which leads to
()
It follows that
()
where
()
Similarly, substituting (47) and (51) into (49), we can get
()
Thus, we have
()
where
()
Thus, we can determine W20(θ) and W11(θ). Furthermore, we can determine each gij. Therefore, each gij is determined by the parameters and delay in (2). Thus, we can compute the following values:
()
which determine the quantities of bifurcating periodic solutions in the center manifold at the critical value τk; that is, μ2 determines the directions of the Hopf bifurcation: if μ2 > 0  (<0), then the Hopf bifurcation is supercritical (subcritical), and the bifurcation exists for τ > τ0  (<τ0); β2 determines the stability of the bifurcation periodic solutions: the bifurcating periodic solutions are stable (unstable) if β2 < 0  (>0); and T2 determines the period of the bifurcating periodic solutions: the period increases (decreases) if T2 > 0  (<0).

4. Numerical Simulations and Application to Control of Chaos

In this section, we apply the results we get in the previous sections to system (61) for the purpose of control of chaos. From Section 2, we know that under certain conditions, a family of periodic solutions bifurcates from the steady states of system (61) at some critical values of τ, and the stability of the steady state may be changed along with the increase of τ. If the bifurcating periodic solution is orbitally asymptotically stable or some steady state becomes local stable, then chaos may vanish. Following this idea, we consider the following delayed feedback control system for an autonomy system:
()
which has two equilibriums, E0(0,0, 0) and E*(9.749,1.9498,9.710). When τ = 0 or K = 0, E0 is unstable and system (61) is chaotic (see Figure 1). The corresponding characteristic equation of system (61) at E0 is
()
When τ = 0, (62) has one negative root and a pair of complex roots with positive parts. By the discussion of Section 2, we can get p = 62.0404 − 0.04K, q = −121.2944 − 2.5616K,   and  r = 60.3418 + 24.8576K, and then we can compute ∆ = 4212.9 + 2.7216K + 0.0016K2, and it is easy to know that ∆>0 and when K ≥ −2.4275, always holds. Then, by Theorem 5, we have the following conclusion.

Conclusion 1. If K < −2.4275 or K ≥ −2.4275 and , then there exist some τ0 > 0, such that when τ ∈ [0, τ0), E0 is always unstable.

For example, we fix K = −1. Through computing, we can get and . Furthermore, we can compute
()
Thus, from Lemma 4, we have
()
In addition, notice that
()
Thus, from (64) and (65), we have the following conclusion about the stability of the zero equilibrium of system (61) and Hopf bifurcations.

Conclusion 2. Suppose that , is defined by (63).

  • (i)

    When , the equilibrium E0 is unstable (see Figures 3, 4, 6, 7, and 8).

  • (ii)

    When , the equilibrium E0 is asymptotically stable (see Figure 5).

  • (iii)

    System (61) undergoes a Hopf bifurcation at the equilibrium E0 when (see Figures 3, 4, and 6).

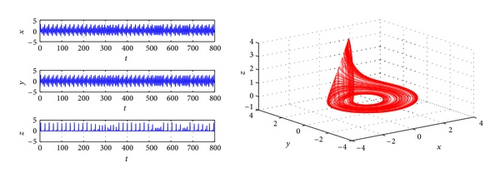
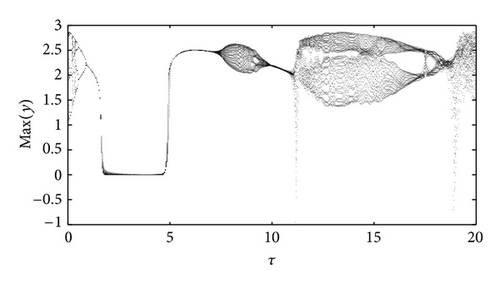
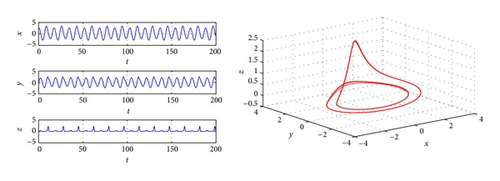
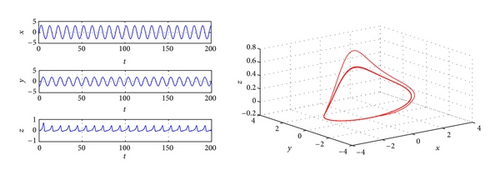
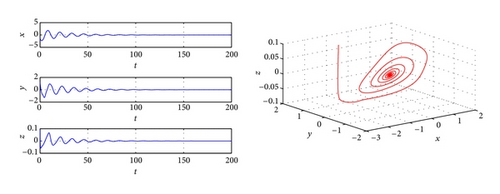
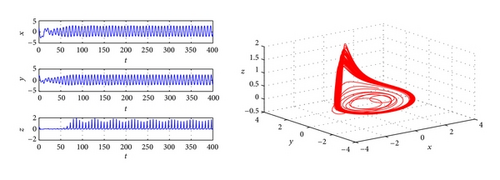
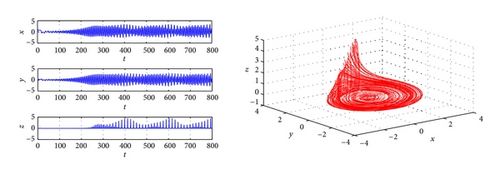
Thus, if we take , the stability of zero equilibrium of the system will change from unstable to stable. For this example, there are more complicated dynamical phenomena occurs. Bifurcation diagram is plotted with the parameter τ when K = −1 (Figure 2). In Figure 2, we can see that chaos vanishes via a period-doubling bifurcation when τ varying from 0 to 0.3768. Figure 3 shows that, when τ = 0.7362, a period-2 orbits bifurcating from zero equilibrium. Figure 4 shows when τ = 1.3497, a period-1 periodical orbits bifurcating from zero equilibrium. In Figure 2, a stable window is obtained from τ = 1.6243 to τ = 5.5173, which is demonstrated by Figure 5 with τ = 2.6815. When τ > 5.5173, Figure 2 shows that periodic orbits and strange attractors also occur, and system (61) through Hopf bifurcation route still goes to chaos, and it is demonstrated by Figures 6–8.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The bifurcation graph with τ when K = −1.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (61) with τ = 0.7362 when K = −1.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (61) with τ = 1.3497 when K = −1.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (61) with τ = 2.6815 when K = −1.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (61) with τ = 6.3804 when K = −1.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (61) with τ = 7.3006 when K = −1.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
The trajectories and phase graphs of system (61) with τ = 13.7423 when K = −1.

5. Discussion

In this paper, an autonomy system with time-delayed feedback is studied by using the theory of functional differential equation and Hassard’s method. Illustrating with numerical simulations, we show that delayed feedback controller (DFC) is an effective method for chaos control.

In fact, system (2) has more complicated dynamical behaves. From Figure 2, we can see that chaos degeneration process, the orbits of system (2) continuously degenerate to a periodic solution region through reverse period-doubling bifurcation. With the increasing of τ, chaos occurs again through Hopf bifurcation route. However, the numerical simulations indicate that there were points of similarity between this route to chaos and quasiperiodicity route to chaos [18]; in our future research, we will consider this topic. And in this paper, we only give detailed analysis on the trivial equilibrium E0; the detailed analysis of the interior equilibrium E* is the second interested topic in our future research.

Acknowledgments

The authors would like to thank the anonymous referee for the very helpful suggestions and comments which led to the improvement of the original paper. And this work is supported by 2013 Scientific Research Project of Beifang University of Nationalities (2013XYZ021), Institute of Information and System Computation Science of Beifang University (13xyb01), Science and Technology Department of Henan Province (122300410417), and Education Department of Henan Province (13A110108).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.