Abstract and Applied Analysis
Volume 2013, Issue 1 134265
Research Article
Open Access

Achieving Synchronization in Arrays of Coupled Differential Systems with Time-Varying Couplings

Xinlei Yi, 

Xinlei Yi

School of Mathematical Sciences, Fudan University, Shanghai 200433, China fudan.edu.cn

Search for more papers by this author
Wenlian Lu, 

Corresponding Author

Wenlian Lu

School of Mathematical Sciences, Fudan University, Shanghai 200433, China fudan.edu.cn

Centre for Computational Systems Biology, Fudan University, Shanghai 200433, China fudan.edu.cn

Centre for Scientific Computing, The University of Warwick, Coventry CV4 7AL, UK warwick.ac.uk

Search for more papers by this author
Tianping Chen, 

Tianping Chen

School of Mathematical Sciences, Fudan University, Shanghai 200433, China fudan.edu.cn

School of Computer Science, Fudan University, Shanghai 200433, China fudan.edu.cn

Search for more papers by this author
First published: 15 July 2013
https://doi.org/10.1155/2013/134265
Citations: 4
Academic Editor: Zidong Wang

Abstract

We study complete synchronization of the complex dynamical networks described by linearly coupled ordinary differential equation systems (LCODEs). Here, the coupling is timevarying in both network structure and reaction dynamics. Inspired by our previous paper (Lu et al. (2007-2008)), the extended Hajnal diameter is introduced and used to measure the synchronization in a general differential system. Then we find that the Hajnal diameter of the linear system induced by the time-varying coupling matrix and the largest Lyapunov exponent of the synchronized system play the key roles in synchronization analysis of LCODEs with identity inner coupling matrix. As an application, we obtain a general sufficient condition guaranteeing directed time-varying graph to reach consensus. Example with numerical simulation is provided to show the effectiveness of the theoretical results.

1. Introduction

Complex networks have widely been used in theoretical analysis of complex systems, such as Internet, World Wide Web, communication networks, and social networks. A complex dynamical network is a large set of interconnected nodes, where each node possesses a (nonlinear) dynamical system and the interaction between nodes is described as diffusion. Among them, linearly coupled ordinary differential equation systems (LCODEs) are a large class of dynamical systems with continuous time and state.

The LCODEs are usually formulated as follows:
()
where t ∈ ℝ+ = [0, +∞) stands for the continuous time and xi(t) ∈ ℝn denotes the variable state vector of the ith node, f : ℝn → ℝn represents the node dynamic of the uncoupled system, σ ∈ ℝ+ = (0, +∞) denotes coupling strength, lij ≥ 0 with i ≠ j denotes the interaction between the two nodes, and , B ∈ ℝn,n denotes the inner coupling matrix. The LCODEs model is widely used to describe the model in nature and engineering. For example, the authors study spike-burst neural activity and the transitions to a synchronized state using a model of linearly coupled bursting neurons in [1]; the dynamics of linearly coupled Chua circuits are studied with application to image processing and many other cases in [2].

For decades, a large number of papers have focused on the dynamical behaviors of coupled systems [3–5], especially the synchronizing characteristics. The word “synchronization” comes from Greek; in this paper the concept of local complete synchronization (synchronization for simplicity) is considered (see Definition 3). For more details, we refer the readers to [6] and the references therein.

Synchronization of coupled systems have attracted a great deal of attention [7–9]. For instances, in [7], the authors considered the synchronization of a network of linearly coupled and not necessarily identical oscillators; in [8], the authors studied globally exponential synchronization for linearly coupled neural networks with time-varying delay and impulsive disturbances. Synchronization of networks with time-varying topologies was studied in [10–16]. For example, in [10], the authors proposed the global stability of total synchronization in networks with different topologies; in [16], the authors gave a result that the network will synchronize with the time-varying topology if the time-average is achieved sufficiently fast.

Synchronization of LCODEs has also been addressed in [17–19]. In [17], mathematical analysis was presented on the synchronization phenomena of LCODEs with a single coupling delay; in [18], based on geometrical analysis of the synchronization manifold, the authors proposed a novel approach to investigate the stability of the synchronization manifold of coupled oscillators; in [19], the authors proposed new conditions on synchronization of networks of linearly coupled dynamical systems with non-Lipschitz right-handsides. The great majority of research activities mentioned above all focused on static networks whose connectivity and coupling strengths are static. In many applications, the interaction between individuals may change dynamically. For example, communication links between agents may be unreliable due to disturbances and/or subject to communication range limitations.

In this paper, we consider synchronization of LCODEs with time-varying coupling. Similar to [17–19], time-varying coupling will be used to represent the interaction between individuals. In [6, 13], they showed that the Lyapunov exponents of the synchronized system and the Hajnal diameter of the variational equation play key roles in the analysis of the synchronization in the discrete-time dynamical networks. In this paper, we extend these results to the continuous-time dynamical network systems. Different from [11, 16], where synchronization of fast-switching systems was discussed, we focus on the framework of synchronization analysis with general temporal variation of network topologies. Additional contributions of this paper are that we explicitly show that (a) the largest projection Lyapunov exponent of a system is equal to the logarithm of the Hajnal diameter, and (b) the largest Lyapunov exponent of the transverse space is equal to the largest projection Lyapunov exponent under some proper conditions.

The paper is organized as follows: in Section 2, some necessary definitions, lemmas, and hypotheses are given; in Section 3, synchronization of generalized coupled differential systems is discussed; in Section 4, criteria for the synchronization of LCODEs are obtained; in Section 5, we obtain a sufficient condition ensuring directed time-varying graph reaching consensus; in Section 6, example with numerical simulation is provided to show the effectiveness of the theoretical results; the paper is concluded in Section 7.

Notions. denotes the n-dimensional vector with all components zero except the kth component 1, 1n denotes the n-dimensional column vector with each component 1; for a set in some Euclidean space U, denotes the closure of U, Uc denotes the complementary set of U, and A∖B = A∩Bc; for , ∥u∥ denotes some vector norm, and for any matrix A = (aij) ∈ ℝn,m, ∥A∥ denotes some matrix norm induced by vector norm, for example, and ; for a matrix A = (aij) ∈ ℝn,m, |A| denotes a matrix with |A | = (|aij|); for a real matrix A, denotes its transpose and for a complex matrix B, B* denotes its conjugate transpose; for a set in some Euclidean space W, 𝒪(W, δ) = {x : dist (x, W) < δ}, where dist (x, W) = inf y∈W ∥x − y∥; #J denotes the cardinality of set J; ⌊z⌋ denotes the floor function, that is, the largest integer not more than the real number z; ⊗ denotes the Kronecker product; for a set in some Euclidean space W, Wm denote the Cartesian product W × ⋯×W (m times).

2. Preliminaries

In this section we will give some necessary definitions, lemmas, and hypotheses. Consider the following general coupled differential system:
()
with initial state , where t0 ∈ ℝ+ denotes the initial time, t ∈ ℝ+ denotes the continuous time, and denotes the variable state of the ith node, i = 1,2, …, m.

For the functions fi : ℝnm × ℝ+ → ℝn, i = 1,2, …, m, we make the following assumption.

Assumption 1. (a) There exists a function f : ℝn → ℝn such that fi(s, s, …, s, t) = f(s) for all i = 1,2, …, m, s ∈ ℝn, and t ≥ 0; (b) for any t ≥ 0, fi(·, t) is C1-smooth for all , and by denotes the Jacobian matrix of with respect to x ∈ ℝnm; (c) there exists a locally bounded function ϕ(x) such that ∥DFt(x)∥≤ϕ(x) for all (x, t) ∈ ℝnm × ℝ+; (d) DFt(x) is uniformly locally Lipschitz continuous: there exists a locally bounded function K(x, y) such that

()
for all t ≥ 0 and x, y ∈ ℝnm; (e) fi(x, t) and DFt(x) are both measurable for t ≥ 0.

We say a function g(y) : ℝq → ℝp is locally bounded if for any compact set K ⊂ ℝq, there exists M > 0 such that ∥g(y)∥≤M holds for all y ∈ K.

The first item of Assumption 1 ensures that the diagonal synchronization manifold
()
is an invariant manifold for (2).
If x1(t) = x2(t) = ⋯ = xm(t) = s(t) ∈ ℝn is the synchronized state, then the synchronized state s(t) satisfies
()

Since f(·) is C1-smooth, then s(t) can be denoted by the corresponding continuous semiflow s(t) = ϑ(t)s0 of the intrinsic system (5). For ϑ(t), we make following assumption.

Assumption 2. The system (5) has an asymptotically stable attractor: there exists a compact set A ⊂ Rn such that (a) A is invariant through the system (5), that is, ϑ(t)A ⊂ A for all t ≥ 0; (b) there exists an open bounded neighborhood U of A such that ; (c) A is topologically transitive; that is, there exists s0 ∈ A such that ω(s0), the ω limit set of the trajectory ϑ(t)s0, is equal to A [3].

Definition 3. Local complete synchronization (synchronization for simplicity) is defined in the sense that the set

()
is an asymptotically stable attractor in ℝnm. That is, for the coupled dynamical system (2), differences between components converge to zero if the initial states are picked sufficiently near 𝒮⋂  Am, that is, if the components are all close to the attractor A and if their differences are sufficiently small.

Next we give some lemmas which will be used later, and the proofs can be seen in the appendix.

Lemma 4. Under Assumption 1, one has

()
for all s ∈ Rn and t ≥ 0, where .

Lemma 5. Under Assumptions 1 and 2, there exists a compact neighborhood W of A such that for all t ≥ t′ ≥ 0 and ⋂t≥0 ϑ(t)W = A.

Let , where δxi(t) = xi(t) − s(t) ∈ ℝn. We have the following variational equation near the synchronized state s(t):
()
or in matrix form:
()
where DFt(s(t)) denotes the Jacobin matrix for simplicity.

From [20], we can give the results on the existence, uniqueness, and continuous dependence of (2) and (9).

Lemma 6. Under Assumption 2, each of the differential equations (2) and (9) has a unique solution which is continuously dependent on the initial condition.

Thus, the solution of the linear system (9) can be written in matrix form.

Definition 7. Solution matrix U(t, t0, s0) of the system (9) is defined as follows. Let U(t, t0, s0) = [u1(t, t0, s0), …, unm(t, t0, s0)], where uk(t, t0, s0) denotes the kth column and is the solution of the following Cauchy problem:

()

Immediately, according to Lemma 6, we can conclude that the solution of the following Cauchy problem
()
can be written as δx(t) = U(t, t0, s0)δx0.
We define the time-varying Jacobin matrix DFt by the following way:
()
with s(t0) = s0, where is the collection of all the subsets of ℝnm,nm.

Definition 8. For a time varying system denoted by Dℱ, we can define its Hajnal diameter of the variational system (9) as follows:

()
where for a ℝnm,nm matrix in block matrix form: with Uij ∈ Rn,n, its Hajnal diameter is defined as follows:
()
where Ui = [Ui1, Ui2, …, Uim].

Lemma 9 (Grounwell-Beesack′s inequality). If function v(t) satisfies the following condition:

()
where b(t) ≥ 0 and a(t) are some measurable functions, then one has
()

Based on Assumption 1, for the solution matrix U, we have the following lemma.

Lemma 10. Under Assumption 1, one has the following:

  • (1)

    , where denotes the solution matrix of the following Cauchy problem:

    ()

  • (2)

    for any given t ≥ 0 and the compact set W given in Lemma 5, U(t + t0, t0, s0) is bounded for all t0 ≥ 0 and s0 ∈ W and equicontinuous with respect to s0 ∈ W.

Let be a ℝnm,nm matrix with Pij ∈ ℝn,n satisfying (a) for some orthogonal matrix P0 ∈ ℝn,n and all i = 1, 2, …, m; (b) P is also an orthogonal matrix in ℝnm,nm. We also write P and its inverse in the form
()
where and P2 ∈ ℝnm,n(m−1). According to Lemma 10, we have
()
Since which implies that each row of is located in the subspace orthogonal to the subspace {1m ⊗ ξ, ξ ∈ ℝn}, we can conclude that . Then, we have
()
where denotes the common row sum of as defined in Lemma 10, , α(t, t0, s0) ∈ ℝn,n(m−1) denotes a matrix, and we omit its accurate expression. One can see that is the solution matrix of the following linear differential system.

Definition 11. We define the following linear differential system by the projection variational system of (9) along the directions P2:

()
where .

Definition 12. For any time varying variational system , we define the Lyapunov exponent of the variational system (9) as follows:

()
where u ∈ ℝnm and s(t0) = s0.

Similarly, we can define the projection Lyapunov exponents by the following projection time-varying variation:
()
that is,
()
where and s(t0) = s0. Let
()

Then, we have the following lemma.

Lemma 13. λP(Dℱ, s0) = log diam(Dℱ, s0).

Remark 14. From Lemma 13, we can see that the largest projection Lyapunov exponent is independent of the choice of matrix P.

Consider the time-varying driven by some metric dynamical system MDS(Ω, ℬ, ℙ, ϱ(t)), where Ω is the compact state space, ℬ is the σ-algebra, ℙ is the probability measure, and ϱ(t) is a continuous semiflow. Then, the variational equation (9) is independent of the initial time t0 and can be rewritten as follows:
()
In this case, we denote the solution matrix, the projection solution matrix, and the solution matrix on the synchronization space by U(t, s0, ω0), , and , respectively. For simplicity, we write them as U(t), , and , respectively. Also, we write the Lyapunov exponents and the projection Lyapunov exponent as follows:
()
We add the following assumption.

Assumption 15. (a) ϱ(t) is a continuous semiflow; (b) DF(s, ω) is a continuous map for all (s, ω) ∈ ℝn × Ω.

The following are involving linear differential systems. For more details, we refer the readers to [21]. For a continuous scalar function u(t), we denote its Lyapunov exponent by
()
The following properties will be used later:
  • (1)

    , where ck, k = 1, 2, …, n, are constants;

  • (2)

    if , which is finite, then χ[1/(u(t))] = −α;

  • (3)

    χ[u(t) + v(t)] ≤ max {χ[u(t)], χ[v(t)]};

  • (4)

    for a vector-value or matrix-value function U(t), we define χ[U(t)] = χ[∥U(t)∥].

For the following linear differential system:
()
where x(t) ∈ ℝn, a transformation x(t) = L(t)y(t) is said to be a Lyapunov transformation if L(t) satisfies
  • (1)

    L(t) ∈ C1[0, +∞);

  • (2)

    L(t), , L−1(t) are bounded for all t ≥ 0.

It can be seen that the class of Lyapunov transformations forms a group and the linear system for y(t) should be
()
where . Then, we say system (30) is a reducible system of system (29). We define the adjoint system of (29) by
()
If letting V(t) be the fundamental matrix of (29), then [V−1(t)] * is the fundamental matrix of (31). Thus, we say the system (29) is a regular system if the adjoint systems (29) and (31) have convergent Lyapunov exponent series: {α1, …, αn} and {β1, …, βn}, respectively, which satisfy αi + βi = 0 for i = 1, 2, …, n, or its reducible system (30) is also regular.

Lemma 16. Suppose that Assumptions 1, 2, and 15 are satisfied. Let {σ1, σ2, …, σn, σn+1, …, σnm} be the Lyapunov exponents of the variational system (26), where {σ1, …, σn} correspond to the synchronization space and the remaining correspond to the transverse space. Let λT(Dℱ, s0, ω0) = max i≥n+1  σi and λS(Dℱ, s0, ω0) = max 1≤i≤n  σi. If (a) the linear system (17) is a regular system, (b) ∥DF(s(t), ϱ(t)ω0)∥ ≤ M for all t ≥ 0, (c) λP(Dℱ, s0, ω0) ≠ λS(Dℱ, s0, ω0), then λT(Dℱ, s0, ω0) = λP(Dℱ, s0, ω0).

3. General Synchronization Analysis

In this section we provide a methodology based on the previous theoretical analysis to judge whether a general differential system can be synchronized or not.

Theorem 17. Suppose that W ∈ ℝn is the compact subset given in Lemma 5, and Assumptions 1 and 2 are satisfied. If

()
then the coupled system (2) is synchronized.

Proof. The main techniques of the proof come from [3, 6] with some modifications. Let ϑ(t) be the semiflow of the uncoupled system (5). By the condition (32), there exist d satisfying and T1 ≥ 0 such that , and . For each s0 ∈ W, there must exist t(s0) ≥ T1 such that for all t0 ≥ 0. According to the equicontinuity of U(t0 + t(s0), t0, s0), there exists δ > 0 such that for any , for all t0 ≥ 0. According to the compactness of W, there exists a finite positive number set 𝒯 = {t1, t2, …, tv} with tj ≥ T1 for all j = 1, 2, …, v such that for any s0 ∈ W, there exists tj ∈ 𝒯 such that diam (U(t0 + tj, t0, s0)) < 1/3 for all t0 ≥ 0. Let x(t) be the collective states {x1(t), …, xm(t)} which is the solution of the coupled system (2) with initial condition , i = 1,2, …, m. And let s(t) be the solution of the synchronization state equation (5) with initial condition . Then, letting Δxi(t) = xi(t) − s(t), we have

()
where , i, j = 1,2, …, m, k, l = 1,2 … , n, are obtained by the mean value principle of the differential functions. Letting , we can write the equations above in matrix form:
()
and denote its solution matrix by . Then, for any t > 0 there exists K2 > 0 such that for all t ∈ 𝒯 and t0 ≥ 0 according to the 3th item of Assumption 1. Then, we have
()
By Lemma 9, we have
()
Let
()
Picking α sufficiently small such that for each x0 ∈ Wα, there exists t ∈ 𝒯 such that and for all t0 ≥ 0.

Thus, we are to prove synchronization step by step.

For any x0 ∈ Wα, there exists t′ = t(x0) ∈ 𝒯 such that

()
Therefore, we have , which implies that and x(t′ + t0) ∈ Wα/2.

Then, reinitiated with time t′ + t0 and condition x(t′ + t0), continuing with the phase above, we can obtain that lim t→∞max i,j∥xi(t) − xj(t)∥ = 0. Namely, the coupled system (2) is synchronized. Furthermore, from the proof, we can conclude that the convergence is exponential with rate O(δt) where , and uniform with respect to t0 ≥ 0 and x0 ∈ Wα. This completes the proof.

Remark 18. According to Assumption 2 that attractor A is asymptotically stable and the properties of the compact neighbor W given in Lemma 5, we can conclude that the quantity

()
is independent on the choice of W.

If the timevariation is driven by some MDS(Ω, ℬ, ℙP, ϱ(t)) and there exists a metric dynamical system {W × Ω, F, P, π(t)}, where F is the product σ-algebra on W × Ω, P is the probability measure, and π(t)(s0, ω) = (θ(t)s0, ϱ(t)ω). From Theorem 17, we have the following.

Corollary 19. Suppose that the conditions in Lemma 16 are satisfied, W × Ω is compact in the topology defined in this MDS, the semiflow π(t) is continuous, and on W × Ω the Jacobian matrix DF(θ(t)s0, ϱ(t)ω) is continuous. Let be the Lyapunov exponents of this MDS with multiplicity and correspond to the synchronization space. If

()
where Ergπ(W × Ω) denotes the ergodic probability measure set supported in the MDS {W × Ω, F, P, π(t)}, then the coupled system (2) is synchronized.

4. Synchronization of LCODEs with Identity Inner Coupling Matrix and Time-Varying Couplings

In this section we study synchronization in linearly coupled ordinary differential equation systems (LCODEs) with time-varying couplings. Considering the following LCODEs with identity inner coupling matrix:
()
where xi(t) ∈ ℝn denotes the state variable of the ith node, f(·) : ℝn → ℝn is a differential map, σ ∈ ℝ+ denotes coupling strength, and lij(t) denotes the coupling coefficient from node j to i at time t, for all i ≠ j, which are supposed to satisfy the following assumption. Here, we highlight that the inner coupling matrix is the identity matrix.

Assumption 20. (a) lij(t) ≥ 0, i ≠ j are measurable and ; (b) there exists M1 > 0 such that |lij(t)| ≤ M1 for all i, j = 1,2, …, m.

Similarly, we can define the Hajnal diameter of the following linear system:

()
Let be the fundamental solution matrix of the system (42). Then, its solution matrix can be written as V(t, t0) = V(t)V(t0) −1. Thus, the Hajnal diameter of the system (42) can be defined as follows:
()

By Theorem 17, we have the following theorem.

Theorem 21. Suppose Assumptions 1, 2, and 20 are satisfied. Let μ be the largest Lyapunov exponent of the synchronized system , that is,

()
If log (diam (ℒ)) + μ < 0, then the LCODEs (41) is synchronized.

Proof. Considering the variational equation of (41):

()
Let be the solution matrix of the synchronized state system (17) and be the solution matrix of the linear system (42). We can see that is the solution matrix of the variational system (45). Then,
()
This implies that the Hajnal diameter of the variational system (45) is less than eμdiam (ℒ). This completes the proof according to Theorem 17.

For the linear system (42), we firstly have the following lemma.

Lemma 22 (see [22].)V(t, t0) is a stochastic matrix.

From Lemmas 13 and 16, we have the following corollary.

Corollary 23. log diam(ℒ) = λP(ℒ), where λP(ℒ) denotes the largest one of all the projection Lyapunov exponents of system (41). Moreover, if the conditions in Lemma 16 are satisfied, then log   diam (ℒ) = λT(ℒ), where λT(ℒ) denotes the largest one of all the Lyapunov exponents corresponding to the transverse space, that is, the space orthogonal to the synchronization space.

If L(t) is periodic, we have the following.

Corollary 24. Suppose that L(t) is periodic. Let ςi, i = 1,2, …, m, are the Floquet multipliers of the linear system (42). Then, there exists one multiplier denoted by ς1 = 1 and .

If L(t) = L(ϱ(t)ω) is driven by some MDS(Ω, ℬ, P, ϱ(t)), from Corollaries 19 and 23, we have the following corollary.

Corollary 25. Suppose L(ω) is continuous on Ω and conditions in Lemma 16 are satisfied. Let , ςi, i = 1,2, …, m, be the Lyapunov exponents of the linear system (42) with ς1 = 0, and . If μ + ς < 0, then the coupled system (41) is synchronized.

Let ℐ be the set consisting of all compact time intervals in [0, +∞) and 𝒢 be the the set consisting of all graph with vertex set 𝒩 = {1,2, …, m}.

Define
()
where G(I, δ) = {𝒩, ℰ} is a graph with vertex set 𝒩 and its edge set ℰ is defined as follows: there exists an edge from vertex j to vertex i if and only if . Namely, we say that there is a δ-edge from vertex j to i across I = [t1, t2].

Definition 26. We say that the LCODEs (41) has a δ-spanning tree across the time interval I if the corresponding graph G(I, δ) has a spanning tree.

For a stochastic matrix , let
()
where vi = [vi1, …, vim], i = 1,2, …, m, and . Then, we can also define that V is δ-scrambling if η(V) > δ.

Theorem 27. Suppose Assumption 20 is satisfied. diam (ℒ) < 1 if and only if there exist δ > 0 and T > 0 such that the LCODEs (41) has a δ-spanning tree across any T-length time interval.

Remark 28. Different from [16], we do not need to assume that L(t) has zero column sums and the timeaverage is achieved sufficiently fast.

Before proving this theorem, we need the following lemma.

Lemma 29. If the LCODEs (41) has a δ-spanning tree across any T-length time interval, then there exist δ1 > 0 and T1 > 0 such that V(t, t0) is δ1-scrambling for any T1-length time interval.

Proof of Theorem 27. Sufficiency. From Lemma 29, we can conclude that there exist δ1 > 0, δ′ > 0, and T1 > 0 such that V(t, t0) is δ1-scrambling across any T1-length time interval and . For any t ≥ t0, let t − t0 = pT1 + T′, where p is an integer and 0 ≤ T′ < T1 and tl = t0 + lT1, 0 ≤ l ≤ p. Then, we have

()
For the first inequality, we use the results in [23, 24]. This implies .

Necessity. Suppose that for any T ≥ 0 and δ > 0, there exists t0 = t0(T, δ), does not have a δ-spanning tree. According to the condition, there exist 1 > d > diam (ℒ), ϵ > 0, and T′ > 0 such that diam (V(t + t0)) < dt for all t0 ≥ 0 and t ≥ T′ and . Thus, picking T > T′, , t1 = t0(T, δ), and , there exist two vertex set J1 and J2 such that if i ∈ J1 and j ∉ J1, or i ∈ J2 and j ∉ J2. For each i ∈ J1 and j ∉ J1, we have

()
Then,
()
Let . According to Lemma 9, we have
()
Similarly, we can conclude that for all l = 1,2. Without loss of generality, we suppose J1 = {1, 2, …, p} and J2 = {p + 1, p + 2, …, p + q}, where p and q are integers with p + q ≤ m. Then, we can write V(T + t1, t1) in the following matrix form:
()
where X11 ∈ ℝp,p and X22 ∈ Rq,q correspond to the vertex subset J1 and J2, respectively. Immediately, we have ∥X12∥∞ + ∥X13∥∞ + ∥X21∥∞ + ∥X23∥∞ ≤ ϵ. Let . We let
()
Let with and p1 = p, p2 = q, p3 = m − p − q. Then,
()
Also,
()
This implies dT ≥ 1 − ϵ which leads contradiction with dT < 1 − ϵ. Therefore, we can conclude the necessity.

5. Consensus Analysis of Multiagent System with Directed Time-Varying Graphs

If we let n = 1, f ≡ 0, and σ = 1 in system (41), then we have
()
In this case, if Assumption 20 is satisfied, then the synchronization analysis of system (57) becomes another important research field named consensus problems.

Definition 30. We say the differential system (57) reaches consensus if for any x(t0) ∈ ℝm, ∥xi(t) − xj(t)∥→0 as t → ∞ for all i, j ∈ 𝒩.

In graph view, the coefficients matrix of (57) L(t) = (lij(t)) ∈ ℝm,m is equal to the negative graph Laplacian associated with the digraph G(t) at time t, where G(t) = (𝒱, ℰ(t), 𝒜(t)) is a weighted digraph (or directed graph) with m vertices, the set of nodes 𝒱 = {v1, …, vm}, set of edges ℰ(t)⊆𝒱 × 𝒱, and the weighted adjacency matrix 𝒜(t) = (aij(t)) with nonnegative adjacency elements aij(t). An edge of G(t) is denoted by eij(t) = (vi, vj) ∈ ℰ(t) if there is a directed edge from vertex i to vertex j at time t. The adjacency elements associated with the edges of the graph are positive, that is, eij(t) ∈ ℰ(t)⇔aij(t) > 0, for all i, j ∈ 𝒩. It is assumed that aii(t) = 0 for all i ∈ 𝒩. The indegree and outdegree of node vi at time t are, respectively, defined as follows:
()
The degree matrix of digraph G(t) is defined as D(t) = diag (degout(v1(t)), …, degout(vm(t))) at time t. The graph Laplacian associated with the digraph G(t) at time t is defined as
()

Let G(I, δ) defined as before. We say that the digraph G(t) has a δ-spanning tree across the time interval I if G(I, δ) has a spanning.

Theorem 31. Suppose Assumption 20 is satisfied. The system (57) reaches consensus if and only if there exist δ > 0 and T > 0 such that the corresponding digraph G(t) has a δ-spanning tree across any T-length time interval.

Proof. Since f ≡ 0, we have μ = 0 in Theorem 21. This completes the proof according to Theorems 27 and 21.

Remark 32. This theorem is a part of Theorem 17 in [25].

6. Numerical Examples

In this section, a numerical example is given to demonstrate the effectiveness of the presented results on synchronization of LCODEs with time-varying couplings. The Lyapunov exponents are computed numerically. By this way, we can verify the the synchronization criterion and analyze synchronization numerically. We use the Rössler system [16, 26] as the node dynamics
()
where a = 0.165, b = 0.2, and c = 10. Figure 1 shows the dynamical behaviors of the Rössler system (60) with random initial value in [0,1] that includes a chaotic attractor [16, 26].
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The dynamical behavior of the Rössler system (60) with a = 0.165, b = 0.2, and c = 10.

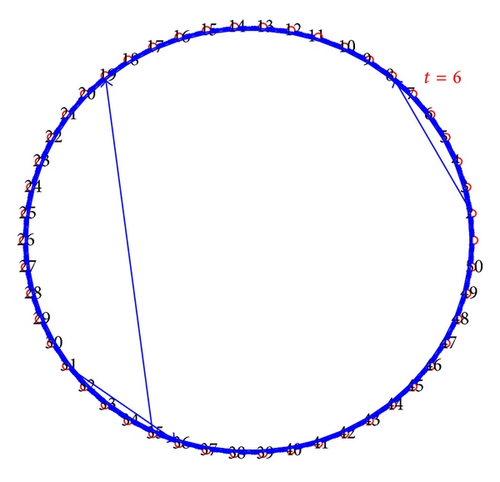
The network with time-varying topology we used here is NW small-world network with a time-varying coupling, which was introduced as the blinking model in [11, 27]. The time-varying network model algorithm is presented as follows: we divide the time axis into intervals of length τ, in each interval: (a) begin with the nearest neighbor coupled network consisting of m nodes arranged in a ring, where each node i is adjacent to its 2k-nearest neighbor nodes; (b) add a connection between each pair of nodes with probability p, which usually is a random number between [0, 0.1]; for more details, we refer the readers to [11]. Figure 2 shows the time-varying structure of shortcut connections in the blinking model with m = 50 and k = 3.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The blinking model of shortcuts connections. Probability of switchings p = 0.04, the switching time step τ = 1.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The blinking model of shortcuts connections. Probability of switchings p = 0.04, the switching time step τ = 1.
In this example, the parameters are taken values as m = 50, k = 3, τ = 1, and p = 0.04. Then blinking small-world network can be generated with the coupling graph Laplacian ℒ(G(t)) = −L(t). The dynamical network system can be described as follows:
()

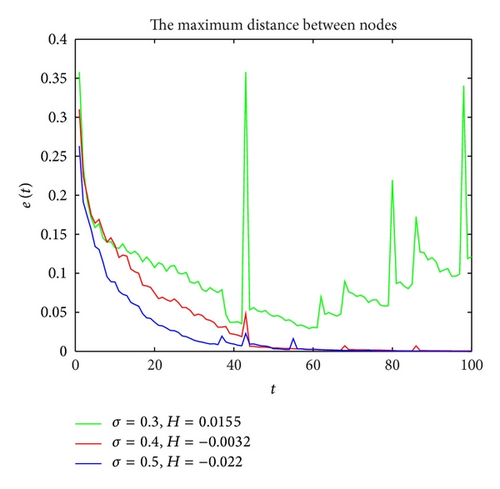
Let e(t) = max 1≤i<j≤50∥xi(t) − xj(t)∥ denotes the maximum distance between nodes at time t. Let , for some sufficiently large T > 0 and R > 0. Let H = μ + ς defined in Corollary 25. As described in Corollary 25, two steps are needed for verification: (a) calculating the largest Lyapunov exponent of the uncoupled synchronized system (60), μ and (b) calculating the second largest Lyapunov exponent of the linear system (42). In detail, we use Wolf′s method [28] to compute μ and the Jacobian method [29] to compute Lyapunov spectra of (42). More details can be found in [28–30]. Figure 3 shows convergence of the maximum distance between nodes during the topology evolution with a different coupling strength σ. It can be seen from Figure 3 that the dynamical network system (61) can be synchronized with σ = 0.4 and σ = 0.5.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Convergence of the maximum distance between nodes with a different coupling strength σ.

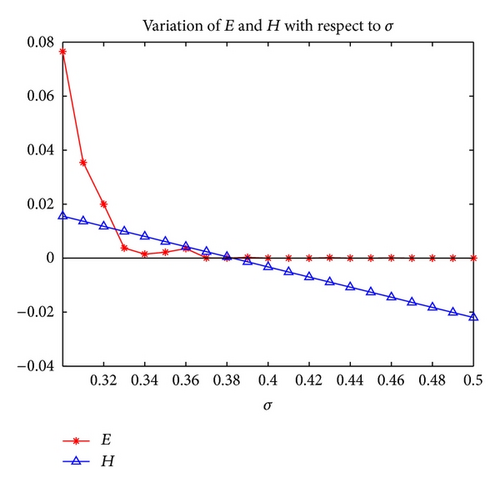
We pick the time length 200. Let T = 190 and R = 10. And choose initial state randomly from the interval [0, 1]. Figure 4 shows the variation of E and H with respect to the coupling strength σ. It can be seen that the parameter (coupling strength σ) region where H is negative coincides with that of synchronization, that is, where E is near zero. This verified the theoretical result (Corollary 25). In addition, we find that σ ≈ 0.38 is the threshold for synchronizing the coupled systems in this case.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Variation of e and H with respect to σ for the blinking topology.

7. Conclusions

In this paper, we present a theoretical framework for synchronization analysis of general coupled differential dynamical systems. The extended Hajnal diameter is introduced to measure the synchronization. The coupling between nodes is timevarying in both network structure and reaction dynamics. Inspired by the approaches in [6, 13], we show that the Hajnal diameter of the linear system induced by the time-varying coupling matrix and the largest Lyapunov exponent of the synchronized system play the key roles in synchronization analysis of LCODEs. These results extend synchronization analysis of discrete-time network in [6] to continuous-time case. As an application, we obtain a very general sufficient condition ensuring directed time-varying graph reaching consensus, and the way we get this result is different from [25]. An example of numerical simulation is provided to show the effectiveness the theoretical results. Additional contributions of this paper are that we explicitly show that the largest projection Lyapunov exponent, the Hajnal diameter, and the largest Lyapunov exponent of the transverse space are equal to each other in coupled differential systems (see Lemmas 13 and 16), which was proved in [6] for couple discrete-time systems.

Acknowledgments

This work is jointly supported by the National Key Basic Research and Development Program (no. 2010CB731403), the National Natural Sciences Foundation of China under Grant (nos. 61273211 and 61273309), the Shanghai Rising-Star Program (no. 11QA1400400), the Marie Curie International Incoming Fellowship from the European Commission under Grant FP7-PEOPLE-2011-IIF-302421, and the Laboratory of Mathematics for Nonlinear Science, Fudan University.

    Appendix

    Proof of Lemma 5. Let U be a bounded open neighborhood of A satisfying and Ut = {x ∈ Rn : ϑ(τ)x ∈ U, 0 ≤ τ ≤ t}. This implies if t′ ≥ t ≥ 0, Ut is an open set due to the continuity of the semiflow ϑ(t), and ϑ(δ)Ut ⊂ Ut−δ for all t ≥ δ ≥ 0. Let V = ⋂t≥0 Ut. We claim that there exists t0 ≥ 0 such that V = Ut for all t ≥ t0.

    For any δ > 0, let tn = nδ and . We can conclude that . We will prove in the following that there exists n0 such that . Otherwise, there always exists xn ∈ Un∖Un+1 for n ≥ 0. Let . We have (i) and (ii) yn ∉ U. For any limit point of yn, can be either finite or infinite. For both cases, which implies . However, the claim (i) implies that , which contradicts with the claim (ii). This completes the proof by letting .

    Proof of Lemma 10. (a) For any initial condition with the form δx0 = 1m ⊗ u0, the solution of (11) can be according to Lemma 4. This implies the first claim in this lemma.

    (b) According to Lemma 5, there exists K1 > 0 such that s(t), the solution of (5), satisfies ∥s(t)∥≤K1 for all s0 ∈ W and t ≥ 0. So, there exists K > 0 such that ∥DFt(s(t))∥≤K according to the 3th item of Assumption 1. Write the solution of (11) δx(t) = U(t, t0, s0)δx0 as

    ()
    Then,
    ()
    According to Lemma 9, we have . This implies that ∥U(t + t0, t0, s0)∥≤eKt for all s0 ∈ W and t0 ≥ 0.

    For any , let s(t) and s′(t) be the solution of the synchronized state equation (5) with initial condition s(t0) = s0 and , respectively. We have

    ()
    By Lemma 9, we have for all t0, t ≥ 0 and . Also, according to the 4th item of Assumption 1, there must exist K2 > 0 such that ∥DFt(s(t)) − DFt(s′(t))∥≤K2∥s(t) − s′(t)∥ for all t ≥ 0 and . Then, let δx(t) = U(t, t0, s0)δx0, , and v(t) = δx(t) − δy(t). We have
    ()
    According to Lemma 9,
    ()
    This implies
    ()
    for all . This completes the proof.

    Proof of Lemma 13. We define the projection joint spectral radius as follows:

    ()
    First, we will prove that diam (Dℱ, s0) = ρP(Dℱ, s0). For any d > ρP(Dℱ, s0), there exists T ≥ 0 such that ≤dt for all t0 ≥ 0 and t ≥ T. This implies that
    ()
    for some C1 > 0, all t0 ≥ 0 and all t ≥ T. Thus, there exist some C2 > 0 and some matrix function q(t) ∈ ℝn,nm such that
    ()
    for all t0 ≥ 0 and t ≥ T, where q(t) ∈ ℝn,nm denotes a matrix, and we omit its accurate expression. So, we can conclude that diam (U(t + t0, t0, s0)) ≤ C3dt for some C3 > 0, all t0 ≥ 0, and t ≥ T. This implies that diam (Dℱ, s0) ≤ d, that is, diam (Dℱ, s0) ≤ ρP(Dℱ, s0) due to the arbitrariness of d ≥ ρP(Dℱ, s0). Conversely, for any d > diam (Dℱ, s0), there exists T > 0 such that
    ()
    for some C4 > 0, all t0 ≥ 0, and t ≥ T, where U1 = [U11, U12, …, U1m] the first n rows of U(t + t0, t0, s0). Then,
    ()
    for some C5 > 0, all t0 ≥ 0, and t ≥ T, where and β(t) ∈ ℝn,n(m−1) denotes a matrix, and we omit its accurate expression. This implies that holds for some C6 > 0, all t0 ≥ 0, and t ≥ T. Therefore, we can conclude that ρP(Dℱ, s0) ≤ d. So, ρP(Dℱ, s0) = diam (Dℱ, s0).

    Second, it is clear that log  ρP(Dℱ, s0) ≥ λP(Dℱ, s0). We will prove that log  ρP(Dℱ, s0) = λP(Dℱ, s0). Otherwise, there exists some r, r0 > 0 satisfying . If so, there exists a sequence tk↑∞ as k → ∞, , and vk ∈ ℝn(m−1) with ∥vk∥ = 1 such that for all k ∈ 𝒩. Then, there exists a subsequence with . Let {e1, e2, …, en(m−1)} be a normalized orthogonal basis of ℝn(m−1). And, let . We have for all j = 1, …, n(m − 1). Thus, there exists L > 0 such that

    ()
    for all l ≥ L. This implies which contradicts with . This implies . Therefore, we can conclude log   diam (Dℱ, s0) = λP(ℱ, s0). The proof is completed.

    Proof of Lemma 16. Let . We have

    ()

    Write , where y(t) ∈ ℝn. Then, we have

    ()
    Thus, we can write its solution by
    ()

    We write λP(Dℱ, s0, ω0), λS(Dℱ, s0, ω0), and λT(Dℱ, s0, ω0) by λP, λS, and λT, respectively for simplicity.

    Case 1 (λP > λS). We can conclude that χ[z(t)] ≤ λP and

    ()
    From Cauchy-Buniakowski-Schwarz inequality, we have
    ()

    Claim 1 (). Considering the linear system

    ()
    due to its regularity and the boundedness of its coefficients, there exists a Lyapunov transform L(t) such that letting u(t) = L(t)v(t), consider the transformed linear system
    ()
    Let solution matrix , which satisfies that and are lowertriangular. And its Lyapunov exponents can be written as follows:
    ()
    which are just the Lyapunov exponents of the regular linear system (A.18), i = 1,2, …, n. We have and
    ()
    This implies
    ()
    By induction, we can conclude that for all j > k. For j < k, due to the lower-triangularity of the matrix .

    Considering the lower-triangular matrix , its transpose can be regarded as the solution matrix of the adjoint system of (A.18):

    ()
    which is also regular. By the same arguments, we can conclude that for all k = 1,2, …, n, for all k > j, and for all k < j. Therefore, for each i > j,
    ()
    This implies that .

    Noting that

    ()
    So, χ[y(t)] ≤ max {λS, λP} = λP. This leads to . This implies that λP = max {λS, λT}. Thus, λP = λT can be concluded due to λP > λS.

    Case 2 (λP < λS). For any ϵ with 0 < ϵ <  (λS − λP)/3, there exists T > 0 such that

    ()

    for all t ≥ T. Define the subspace of ℝnm:

    ()
    which is well defined due to . For each with initial condition , we have χ[z(t)] ≤ λP and
    ()
    according to the arguments above. Thus, we have max u∈V  λ(Dℱ, u, s0, ω0) = λP. Since dim (V) = n(m − 1), V define the transverse space and λT = λP. This completes the proof.

    Proof of Lemma 22. Since L(t) satisfies Assumption 20, if the initial condition is u(t0) = 1m, then the solution must be u(t) = 1m, which implies that each row sum of V(t, t0) is one. Then, we will prove all elements in V(t, t0) are nonnegative. Consider the ith column of V(t, t0) denoted by Vi(t, t0) which can be regarded as the solution of the following equation:

    ()
    For any t ≥ t0, if i0 = i0(t) is the index with , we have . This implies that min i=1,2,…,m    ui(t) is always nondecreasing for all t ≥ t0. Therefore, ui(t) ≥ 0 holds for all i = 1,2, …, m and t ≥ t0. We can conclude that V(t, t0) is a stochastic matrix. The proof is completed.

    Proof of Lemma 29. Consider the following Cauchy problem:

    ()
    Noting that , we have . For each i ≠ k, since ui(t) ≥ 0 for all i = 1,2, …, m and t ≥ t0, we have
    ()
    So, if there exists a δ-edge from vertex j to i across [t0, t0 + T], then we have . Let . We can see that V(t, t0) has a δ2 spanning tree across any T-length time interval. Therefore, according to [31, 32], there exist δ1 > 0 and T1 = (m − 1)T such that V(t, t0) is δ1 scrambling across any T1-length time interval. The Lemma is proved.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.