Abstract and Applied Analysis
Volume 2013, Issue 1 131207
Research Article
Open Access

Construction of Target Controllable Image Segmentation Model Based on Homotopy Perturbation Technology

Shu-Li Mei, 

Corresponding Author

Shu-Li Mei

College of Information and Electrical Engineering, China Agricultural University, Postbox 53, East Campus, 17 Qinghua Donglu Road, Haidian District, Beijing 100083, China ncsu.edu

Search for more papers by this author
First published: 24 February 2013
https://doi.org/10.1155/2013/131207
Citations: 7
Academic Editor: Lan Xu

Abstract

Based on the basic idea of the homotopy perturbation method which was proposed by Jihuan He, a target controllable image segmentation model and the corresponding multiscale wavelet numerical method are constructed. Using the novel model, we can get the only right object from the multiobject images, which is helpful to avoid the oversegmentation and insufficient segmentation. The solution of the variational model is the nonlinear PDEs deduced by the variational approach. So, the bottleneck of the variational model on image segmentation is the lower efficiency of the algorithm. Combining the multiscale wavelet interpolation operator and HPM, a semianalytical numerical method can be obtained, which can improve the computational efficiency and accuracy greatly. The numerical results on some images segmentation show that the novel model and the numerical method are effective and practical.

1. Introduction

In general, choosing different parameters in the most common image segmentation methods usually leads to different image segmentation results [1]. In other words, the object segmentation results are uncontrollable by the common methods. To solve the problem, one of the most common strategies is choosing thresholds using prior knowledge or analyzing the distribution of gray values of an image with the gray value histogram. Another method is image enhancement, which can often destroy the contour of the objects.

The variational method on image segmentation is a new image processing technology, which processes lots of better properties in processing medical images such as MRI and CI [2]. In this method, the pictures are taken as continuous energetic fields, and so the corresponding information in digital images such as gradient, divergence, and the curvature of the object contour can be viewed as the differential operators embedded in the variational model on image processing. The traditional complicated image processing such as denoising with texture preserving and exact segmentation can be done by this model. The outstanding work of this field is the energy function for image segmentation proposed by Mumford and Shah, which has been widely used, and its mathematical properties are well analyzed. This is a general approach on image segmentation, where it is assumed that objects can be characterized by smooth surfaces or volumes in three dimensions. In order to solve the Mumford-Shah model with the Euler-Lagrange method, a simplified model was deduced by Chan and Vese, in which the Euclid length was employed instead of the Hausdorff length [3]. So, the simplified model is also called Chan-Vese model. Similar to other image segmentation methods, Chan-Vese model cannot identify the object as well. Multilevel set approach for solving C-V model can segment all the objects in a picture. But it will obviously lead to oversegmentation [4].

In many cases, the purpose of the image segmentation is to get one special single object instead of all the objects in a multiobject image. Therefore, the purpose of this paper is to construct a target controllable image segmentation model based on the basic idea of homotopy perturbation technology (HPM). Using the variational method, the optimal solution of the energy function can be expressed as a nonlinear partial differential equation. So, another task of this study is to construct an effective numerical method on nonlinear PDEs by combining the multiscale wavelet interpolation operator and the homotopy perturbation method. The homotopy perturbation method (HPM) proposed by He [5, 6] is constantly being developed and applied to solve various nonlinear problems by He [7–15] and by others [16–20]. The better improvement is adding an auxiliary parameter into the homotopy equation, which is helpful to eliminate the secular term in the perturbation solution. This can improve the rate of convergence greatly. Unlike analytical perturbation methods, HPM does not depend on small parameter which is difficult to find. The variational iteration method was another simple and effective method for nonlinear equations proposed by He [21–26], which can provide analytical approximations to a rather wide class of nonlinear equations [27–33] without linearization, perturbation, or discretization which can result in massive numerical computation. In order to solve the nonlinear PDEs, it is necessary to introduce the wavelet numerical algorithm [34–37] into HPM.

2. Construction of Target Controllable Image Segmentation Model

In order to solve the Mumford-Shah model with the Euler-Lagrange method, a simplified model was deduced by Chan and Vese, in which the Euclid length was employed instead of the Hausdorff length. This simplified model can also be called the Chan-Vese model, which can be expressed as follows:
()
where λ1 and λ2 are positive constants and c1 and c2 are the average gray level values inside (Ω1) and outside (Ω2) of the object contour, respectively. I0 denotes the image to process, |C| is the length of the object contour, and ν is the weight parameter. According to the level set method, the contour curves of the objects should be embedded into the level set function as follows:
()
Then, the level set-based C-V model can be rewritten as follows:
()
Using the variational method, the PDEs with respect to the variable ϕ can be obtained as follows:
()
Obviously, div (∇ϕ/|∇ϕ|) is the curvature of the level set function ϕ, and δε(ϕ) is used to constrain the growth of the level set function.

The solution of (4) is the level set function ϕ(x, y, t) at time t. The zero level set is the object contour curve, which can be obtained by solving ϕ(x, y, t) = 0.

In the following, what we are talking about is how to construct the target controllable image segmentation model based on the basic idea of HPM. It is easy to understand that the function of the curvature in C-V model is just to preserve the smoothness of the object contour. Neglecting the curvature in (4), the simplified model can be obtained as follows:
()
In solving the C-V model with HPM and iteration method, the average gray level values inside and outside of the contour curves c1 and c2 vary with the evolution of the level set function. This evolution will end up with that the contour curve coincides with the object boundary. Then, c1 and c2 become constants, and the right hand of (5) should equal zero; that is,
()
In general, λ1 and λ2 are constant, which are correlated to c1 and c2 obviously.
It is easy to understand that the segmentation results and the values of c1/c2 are in one-to-one correspondence with each other. So, the object segmentation can be controlled by the value of (λ1/λ2). Let k = λ1/λ2, m = c1/c2, and substitute k, m into (5), we can obtain
()
Let
()
It is obviously that F(I0) = 0 is the necessary condition for the functional extremum problem about C-V model. The solution of the necessary condition is
()
In the end of the image segmentation processing, the gray level value I0 of the pixel inside the object contour equals c2; that is, I0 = c2  (in  Ω2). Then, the relation between the parameter k and the average gray level value of the image can be expressed as
()
In the end of the image segmentation procedure, the final c1 and c2 should be coincident with average gray level values inside and outside of the segmentation target, respectively. They can be determined in advance by the priori knowledge. But in the beginning of the image segmentation processing, c1 and c2 are the average gray level values inside and outside of the zero level set, respectively. They are determined by the position of the level set function, which is random in most cases. It is easy to understand that there is a continuous map between the two cases, that is, the connection between the two cases can be set up by the HPM. In other words, the parameter k in (10) can be taken as the homotopy parameter; then, a linear homotopy function for (4) can be constructed as
()
where the homotopy parameter p ∈ [1, k], k is determined by the final c1 and c2 based on the priori knowledge in advance and ν is a weight parameter. α is an auxiliary parameter, which can be identified by eliminating the secular term in the perturbation analytical solution.

Equation (11) is the target controllable image segmentation model. It should be pointed out that the auxiliary parameter α appearing in this model is set to zero, as there is no any secular term in the perturbation analytical solution.

3. HPM on Nonlinear System Based on the Multilevel Wavelet Analysis

3.1. Wavelet Numerical Discretization Schemes on C-V Model

The definition domain of the image is defined as (xmin , xmax )×(ymin , ymax ), which should be divided evenly into 2j × 2j (j is the level number) subdomains according to the wavelet collocation method. The connection nodes between two adjoining subdomains are the discretization points defined as , where
()
In addition, denotes the multiscale wavelet function and the corresponding mth and nth derivatives with respect to x and y, respectively. The level set function ϕ(x, y, t) and the corresponding derivative function can be descretized as follows:
()
where j and J are constants, which denote the wavelet scale number and the maximum of the scale number, respectively. , , and are the wavelet coefficients at the discretization point .
According to above definitions, the curvature of the level set ϕ(x, y, t) can be expressed approximately as
()
Substituting (14) and (13) into (11), we obtain
()

Obviously, (15) is a nonlinear ordinary differential equation.

3.2. HPM on Discretization Format of C-V Model

There are various ways to construct a homotopy function. For (15), a linear homotopy function can be constructed as
()
where
()
where ν is the weight parameter. According to the perturbation theory, the solution of (16) can be expressed as the power series expansion of p
()
Substituting (18) into (16) and rearranging based on powers of ε-terms, we have
()
where f1 and f2 are functions with respect to ε1 and ε2, respectively. It is easy to identify the homotopy parameter as
()
Thus, based on the definition of the Taylor series, can be identified as (tn+1 − tn)Fn, and f1 can be identified as
()
Substituting and into (18) and assuming ε = 1, the numerical solution of (16) can be obtained subsequently:
()
Then, the wavelet coefficient can be obtained as follows:
()
where
()
is the quasi-Shannon wavelet function; that is,
()
Substituting the three wavelet coefficients into (16), ϕJ(m,n)(x, y, tn+1) can be obtained; then we can obtain Fn+1 as follows:
()
At last, we can obtain the image segmentation result expressed in the level set as follows:
()

4. Numerical Experiences and Discussion

In this section, we take some multiobject images as examples to illustrate the efficiency of the target controllable image segmentation model compared with the C-V model. The original image showed in Figure 1 consisted of three geometrical solid objects. The color of the background is white, and whole area is 1. The gray level values and the areas of the three objects are showed in Table 1. The image segmentation aims to get the circular and the rectangular objects. In other words, we want to take the black elliptical object as the background.

Table 1. The gray level values and areas of all objects.
  Ellipse Circle Squareness Background
Gray level value 0 163 7 255
Area 0.0568 0.0723 0.0733 0.7976
Details are in the caption following the image
Figure 1 (a) Original image
Open in figure viewerPowerPoint
Multiobject image segmentation at k = 1 (λ1 = λ2 = 10, Δt = 10).
Details are in the caption following the image
Figure 1 (b) 10 iteration times
Open in figure viewerPowerPoint
Multiobject image segmentation at k = 1 (λ1 = λ2 = 10, Δt = 10).
Details are in the caption following the image
Figure 1 (c) 50 iteration times
Open in figure viewerPowerPoint
Multiobject image segmentation at k = 1 (λ1 = λ2 = 10, Δt = 10).
Details are in the caption following the image
Figure 1 (d) 500 iteration times
Open in figure viewerPowerPoint
Multiobject image segmentation at k = 1 (λ1 = λ2 = 10, Δt = 10).
Details are in the caption following the image
Figure 1 (e) 750 iteration times
Open in figure viewerPowerPoint
Multiobject image segmentation at k = 1 (λ1 = λ2 = 10, Δt = 10).
Details are in the caption following the image
Figure 1 (f) 1000 iteration times
Open in figure viewerPowerPoint
Multiobject image segmentation at k = 1 (λ1 = λ2 = 10, Δt = 10).

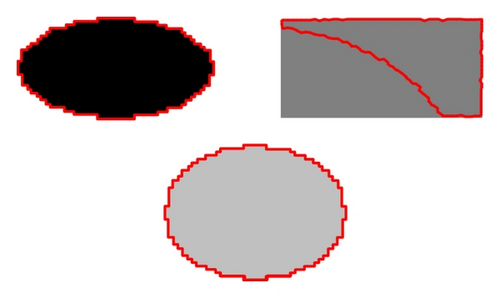
The segmentation results of C-V model are showed in Figure 1. With the increasing of the iteration times, the rectangular object becomes a part of the background gradually instead of the elliptical object, which does not meet our requirement obviously.

The segmentation results with the target controllable model are showed in Figure 2. The final c1  =  255 × 0.7976/(0.7976 + 0.0568) = 238.05, and c2  =  (163 × 0.0723 + 7 × 0.0733)/(0.0723 + 0.0733) = 86.464. It should be pointed out that the final c1 and c2 can be obtained by priori knowledge in most cases. At the beginning of the segmentation, all the three objects are obtained as the foreground. With the increasing of the iteration times, the black object is gradually pushed into the background and out of the object region.

Details are in the caption following the image
Figure 2 (a) 10 iteration times
Open in figure viewerPowerPoint
Multitarget image segmentation with target controllable model.
Details are in the caption following the image
Figure 2 (b) 1000 iteration times
Open in figure viewerPowerPoint
Multitarget image segmentation with target controllable model.

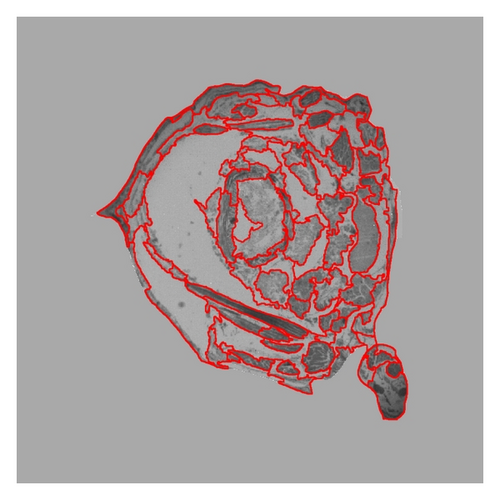
Figure 3 is an enlarged local image of the locust body cavity. The objects have an irregular shape with a slightly serrated border which can introduce over an insufficient segmentation. So it is difficult to segment with other methods. Using the target controllable model, we can get the right object easily. This example shows that the novel model and the corresponding numerical method are practical. Indeed, the novel model has been used to segment the locust’s coelom images (Figure 4).

Details are in the caption following the image
Figure 3 (a) C-V model
Open in figure viewerPowerPoint
Special object segmentation.
Details are in the caption following the image
Figure 3 (b) Target controllable model
Open in figure viewerPowerPoint
Special object segmentation.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Locust’s coelom image segmentation results by the target controllable model.

5. Conclusions

C-V model is a kind of the modified Mumford-Shah model which has been widely used in medical images, and its mathematical properties are well analyzed. But the segmentation result is usually uncontrollable. The target controllable image segmentation model proposed in this paper is based on the idea of HPM. The numerical experiences show that the novel model and the corresponding numerical algorithm are effective and practical. It meets the requirement of the medical images segmentation.

Acknowledgment

This work is supported by the National Natural Science Foundation of China under Grant no. 41171337 and National Key Technologies R & D Program of China under Grant no. 2012BAD35B02.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.