The most probable failure mode of FRP-strengthened RC beams is an intermediate crack-induced debonding. Over the last 13 years, researchers developed several methods for calculation strain corresponding to delamination of FRP. A significant number and diversity of existing foreign and domestic methods make the design complex process. The aim of this study was to propose a simple method for calculating FRP debonding strains, based on the best international achievements and adapted for use in Russia. To achieve this goal, the authors performed a review and reliability assessment of existing foreign and domestic meth-ods. Reliability assessment is made by comparing the calculated and experimental data. Experimental data were collected from the existing literature. After reliability assessment, the most simple and accurate method was selected among the considered. On the basis of the chosen method, the authors proposed a formula for calculating the design value and characteristic value strain corresponding to delamination of FRP. The results of calculations by the authors’ formula are more economical than the original method and have the required reliability for these variables. The proposed method is recommended for use in the design of flexural FRP-strengthened RC beams in Russia.

1. Introduction

The technology of externally bonded FRP systems for strengthening reinforced concrete (RC) beams has become a popular technology in Russia in recent years. Strengthening flexural elements is done by bonding of a FRP plate to the tension face of a beam. FRP-strengthened RC beams may present some failure modes:

(1)
steel yield and FRP rupture;
(2)
steel yield and concrete crushing;
(3)
concrete compression failure;
(4)
shear failure;
(5)
flexure crack-induced interfacial debonding;
(6)
flexural-shear crack-induced interfacial debonding;
(7)
concrete cover separation;
(8)
plate-end interfacial debonding;
(9)
peeling off caused by the unevenness, irregularities, and roughness of the concrete surface.

All of these typical failure modes are recognized for flexural FRP-strengthened members and are widely reported in the scientific literature [1–6]. Modes (1)–(4) are similar to conventional bending failure of reinforced concrete elements. Modes (5)–(9) are unique and peculiar to the structures reinforced by externally bonded FRP systems. These modes failures usually occur before ultimate bearing capacity of the structure to bending or shear achieved. In practice modes (7)-(8) are often eliminated by gluing to the support element areas anchorage transverse U-shaped hoop. Mode (9) is prevented by quality surface preparation. Modes (5)-(6) are generally defining the design. To prevent such an intermediate crack-induced debonding failure mode at ULS, the strain (stress) in FRP reinforcement should be limited to the level at which debonding may occur due to the opening of flexural flexural-shear cracks in the beam’s tension zone in the middle of the span.

Calculation of FRP strain corresponding to delamination is set out in a number of foreign guidelines [7–11]. This issue is also dealt with in [12–14].

Today in Russia, there is no national code for the design and construction of externally bonded FRP systems for strengthening concrete structures. At the end of 2012 it was proposed to discuss the first draft of the code “strengthening of reinforced concrete structures with composite materials” [15]. The draft is developed by the Research, Design and Technological Institute for Concrete and Reinforced Concrete named after Gvozdev supported by a number of interested companies, long before the draft methodology for the design and construction of externally bonded FRP systems for strengthening concrete structures were presented at a number of guides, which do not have the status of national standard [16–21]. These guides are designed by the foreign companies-suppliers of technologies and materials in Russia or by domestic institutions on the orders of these companies.

Calculation of FRP strain corresponding to delamination stated in the draft and some guides is taken from “manual for strengthening reinforced concrete structures with composite materials” [16]. In the guide of “BASF Building Systems” company [20] (further STO BASF) and handbook [21] (further handbook fife), the methods of calculating of FRP strain corresponding to delamination are adaptations of the approach outlined in the ACI 440.2R-08 [7]. Strictly speaking, the approach outlined in the manual [16] was also borrowed from the earlier edition of ACI 440.2R-02 [22].

Thus, the development of Russia’s standard framework for enhancing structure by FRP has gone the way of borrowing foreign developments. However, the choice of a basic methodology for calculating of FRP strain corresponding to delamination remains unclear. Why the American approach was formed on the basis of the existing Russian practices?

The aim of this study is to propose a simple and cost-effective model for the calculation of FRP strain corresponding to delamination. To achieve this goal, we will accomplish the following tasks:

(1)
perform a review of the existing foreign and domestic methods of calculating of FRP strain corresponding to delamination;
(2)
fulfill their verification and reliability assessment;
(3)
choose among the considered the most reliable method to assess its shortcomings;
(4)
make the necessary adjustments to the selected model to reduce its weaknesses and adaptation to Russian regulatory basis of values and notation;
(5)
assess the reliability of the proposed model.

2. A Review of Existing Theoretical Models

A detailed review of foreign and domestic methods sets out in a companion paper [23]. Here is a review of some of the methods developed by foreign researchers and not included in the codes.

2.1. Teng et al

The model for predicting intermediate crack-induced debonding failure [12] is based on a bond strength model [24]. The stress in the bonded plate to cause debonding failure in simple shear tests is expressed by

()

where E_f, t_f, and b_f are the elastic modulus (MPa), thickness (mm), and width (mm) of the bonded plate, respectively, and b_c are the specified cylinder compressive strength (MPa) and width (mm) of the concrete block, respectively, L is the bond length (mm), and L_e is the effective bond length (mm). A value of 0.427 for α was found by authors [24] to provide a best fit of the shear test data gathered by them.

In [12], the coefficient α in (1) was recalibrated against the collected test data of beams and cantilever slabs failing by intermediate crack debonding. The authors used the 8 experimental results for beams and 6 results for cantilever slabs. It was proposed that a value of 0.48 for α is adopted for design use, which leads to conservative predictions for all test results of the combined database. Note that the experimental data used by the authors had a wide scatter.

Additionally, the authors noted that for simply supported beams with a plate terminated near the supports or cantilever beams and slabs with the plate terminated near the free end, the bond length is generally greater than the effective bond length, so β_L is generally equal to 1.0.

2.2. Lu et al

In [13], the authors have presented a finite-element (FE) model based on the smeared crack approach for concrete for the numerical simulation of the IC debonding process. The FE model was shown to be accurate through comparisons with the results of 42 beam tests. Based on interfacial shear stress distributions from finite-element analyses and bond-slip model, presented in [25], the authors obtained a simple analytical model for calculating the FRP strain corresponding to delamination. The new strength model was shown to be accurate through comparisons with the test results of 77 beams. The strain in the FRP plate at the critical section when IC debonding occurs can then be obtained from

()

where L_d is the distance (mm) from the loaded section to the end of the FRP plate, f_t is the tensile strength of concrete (MPa), and τ_max is the maximum shear bond stress (MPa).

We note that 99% of experiments to study the flexural FRP-strengthened elements are organized in the form of 3- or 4-point bending tests. Thus, loading performed by concentrated forces. However, in a real design, calculation of bending elements is performed on a distributed load act; that is, it is not possible to determine L_d.

2.3. Said and Wu

In [14], the authors approved that the critical value for the FRP strain at debonding may be expressed by

()

where C₁ = 0.23, C₂ = 0.2, C₃ = 0.35 are constants that were obtained determined from the available experimental result. For design purposes, a strength reduction factor of 0.75 was recommended.

2.4. Comparison of the Models

In this paper and in the companion paper [23], methods for calculation of FRP strain corresponding to delamination are summarized in Table 1. None of the methods of calculation do involve separate design and characteristic values of the strain. Nevertheless, Table 1 shows the formula to calculate these values individually. This separation must be done artificially and for subsequent evaluation of the reliability of methods. In the event that the original source did not specify the formula used to calculate the characteristic value, it was considered that the formula to estimate the design value. The formula for calculating the characteristic value is obtained by eliminating any of the safety factors.

Table 1. Existing theoretical models and guidelines.

No.	Formula		Reference
No.	Characteristic value of FRP debonding strain	Design value of FRP debonding strain	Reference
1		, , ψ_f = 0.85	[7]

2	,	, , γ_f,d = 1.2, γ_c = 1.5	[8]

3	—	, Γ_Fk = 0.5	[11]

4	,	—	[12]

5	—	(4.41 − α) , , τ_max = 1.5k_bf_t,	[13]

6	—		[14]

7	,	,
			[16–19]
		, γ_f = 1.1	[16–19]

8		, , γ_f1 = 0.9,	[20]

9		, , ,	[21]

10	,	,
			[15]
		,

is the specified compressive strength of concrete; n is the number of plies of FRP reinforcement; E_f is the tensile modulus of elasticity of FRP; t_f is the nominal thickness of one ply of FRP reinforcement; is the ultimate rupture strain of FRP reinforcement; is the design rupture strain of FRP reinforcement; ψ_f is the FRP strength reduction factor; C_E is the environmental reduction factor; γ_f,d, γ_f, γ_f1, γ_f2, γ_E,f, γ_m, γ_ε,f are the partial factors; γ_c is the partial factor for concrete; Γ_Fk is the characteristic value of specific fracture energy; τ_max is the maximum shear bond stress; L_d is the distance from the loaded section to the end of the FRP plate; f_t is the tensile strength of concrete; k_m is the bond-dependent coefficient; R_b,n, characteristic value of compressive strength of concrete in compliance with Russian codes; B strength classes for concrete in compliance with Russian codes.

Since the notations of the same quantities of the various authors are different, the following notations have been introduced in Table 1: ε_fd is the FRP debonding strain, b_f is the width (mm) of the bonded plate, b is the width (mm) of the concrete member, and k_b is the geometrical factor related to the width of the bonded plate and the width of the concrete member.

A review of the existing foreign and domestic methods of calculating of FRP strain corresponding to delamination showed that neither abroad nor in Russia there is consensus on this issue. The following questions remain open: which of the methods more accurately predicts the actual value of the debonding strains? What is the reliability with which this prediction is performed?

Domestic approaches contained all sorts of safety factors, which complicates the calculation formula. It is not clear how these factors actually increase the reliability of the debonding strains.

It is important to note that the approach outlined in ACI 440.2R-08 [7], and hence the domestic approaches, based entirely on ACI 440 [7, 22], did not take into account the geometrical factor related to the width of the bonded plate and the width of the concrete member, which can reduce the accuracy of calculation.

Many foreign methods used the specified compressive strength of concrete

to calculate the debonding strains. In Russian codes, the main characteristics of strength of concrete are the characteristic R_b,n and design R_b values of compressive strength of concrete and strength class for concrete B. The cylinder strength in ACI 318 also has to be converted to the characteristic cylinder strength f_ck in European codes and then to the characteristic value of compressive strength of concrete R_b,n in Russian codes. Because

only represents a 9% fractile, whereas f_ck is a 5% fractile value, the following relationship can be derived [26]:

()

In EN 1992-1-1 [27], the 2 : 1 cylinder strength is taken to be about 20% less than the cube strength for normal structural concrete, f_ck = 0.8f_ck,cube. The characteristic cube strength f_ck,cube with probability 5% in European codes is the same as the strength class for concrete B in Russian codes. Consider.

()

In Russian codes, the characteristic value of compressive strength of concrete can be expressed in terms of strength class by

()

Then, we can write the following equation:

()

The design value of compressive strength of concrete R_b is the ratio of the characteristic value of compressive strength of concrete R_b,n and the partial factor for concrete γ_c = 1.3.

The analysis of all the considered methods can provide debonding strains of the FRP in the form of the following function:

()

where α is the empirical coefficient; k_b is the geometrical factor related to the width of the bonded plate and the width of the concrete member; R is the some concrete strength; C₁ is the value of the degree of strength of concrete; n is the number of plies of FRP reinforcement; E_f is the tensile modulus of elasticity of FRP; t_f is the nominal thickness of one ply of FRP reinforcement; C₂ is the value of the degree of longitudinal stiffness of the composite. The study is required to determine the values of α, C₁, and C₂ and decide in what forms to enter in a formula the strength of concrete is.

3. Experimental Database

In the present study, a wide database, which was assembled by collecting data of experimental tests on FRP-strengthened RC beams that failed by IC debonding, has been used. In construction of the database, reported test results were not included if they had any of the following characteristics:

(1)
beams failed due to concrete cover separation or plate-end interfacial debonding;
(2)
no debonding strains were provided;
(3)
it is not clear which strength of concrete is specified: cylinder or cube;
(4)
beams are with anchorage details along span.

Out of a total of 22 experimental studies, only 14 had some specimens satisfying the previous requirements, resulting in a total of 83 beams or slabs included in the database. The selected members represent a wide cross section of shapes and sizes, with widths varying from the lower limit of 100 mm up to 400 mm. The reinforcement ratio varies from 0.33% to 1.71%. The spans range from 1500 to 6000 mm. The database includes three different FRP materials: CFRP, aramid FRP (AFRP), and glass FRP (GFRP), which were installed using both the wet lay-up method and externally bonding a pre-cured laminate using structural adhesive. Figure 1 shows the regression lines, which are reflecting the relationship between experimental values of the debonding strains and corresponding values obtained by calculation. Note that in some cases, debonding strains calculation involves first payment rupture strain. In the calculation of the rupture strain, the partial factors C_E, γ_E,f, and γ_ε,f were not considered, since the comparison was performed with the results of short-term tests; that is, the environmental impact was negligible.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Experimental versus theoretical debonding strains.

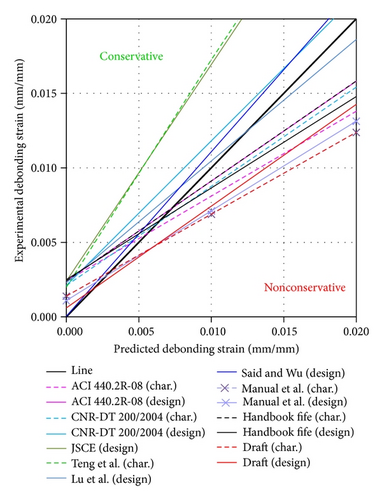
The ordinates are the experimental values of the debonding strains (marked ε_fd,ex.), and the abscissae are the predicted (theoretical) values of design and characteristic values of the debonding strains (marked ε_fd,th.). The plotting area is divided into two areas: the area of conservative results, ε_fd,ex. > ε_fd,th., and the area of unconservative results, ε_fd,ex. < ε_fd,th.. The line (bold) corresponds to the equality ε_fd,ex. = ε_fd,th.. The data in Figure 1 allow you to visually assess the reliability of different methods.

For comparison between the considered models, a statistical analysis was performed using the program “STATISTICA.” Graphical representations were obtained in which one can assess the performance of the models against the experimental database. For any model, the mean and standard deviation were found for the variables

()

In order to use the normal distribution to predict the behavior of the model, the Kolmogorov-Smirnov and Lilliefors tests and Shapiro-Wilk’s W test were used to determine the goodness of fit. A percentage of exceedance value was also found for each analytical model. This represents the probability that the analytical model will overestimate the IC debonding failure, judged from the sample of experimental beams. The results of statistical analysis are shown in Tables 2 and 3. In Figures 2 and 3 the normal distributions for x₁ and x₂ are shown.

Table 2. Results of statistical modeling of x₁.

Kolmogorov-Smirnov and Lilliefors tests	Shapiro-Wilk’s W test	Mean, theor/exp	Standard deviation	Probability of exceedance	Reference
K-S d = 0.0878, P > 0.20; Lilliefors P < 0.15	W = 0.971, P = 0.059	1.171	0.324	70%	[7]
K-S d = 0.069, P > 0.20; Lilliefors P > 0.20	W = 0.971, P = 0.066	1.126	0.287	67%	[8]
—	—	—	—	—	[11]
K-S d = 0.093, P > 0.20; Lilliefors P > 0.20	W = 0.963, P = 0.089	0.467	0.061	0%	[12]
—	—	—	—	—	[13]
—	—	—	—	—	[14]
K-S d = 0.075, P > 0.20; Lilliefors P > 0.20	W = 0.979, P = 0.228	1.494	0.380	90%	[16–19]
K-S d = 0.096, P > 0.20; Lilliefors P < 0.10	W = 0.974, P = 0.107	1.362	0.375	83%	[20]
K-S d = 0.083, P > 0.20; Lilliefors P < 0.20	W = 0.972, P = 0.078	1.082	0.314	60%	[21]
K-S d = 0.082, P > 0.20; Lilliefors P > 0.20	W = 0.983, P = 0.374	1.479	0.358	91%	[15]

Table 3. Results of statistical modeling of x₂.

Kolmogorov-Smirnov and Lilliefors tests	Shapiro-Wilk’s W test	Mean, theor/exp	Standard deviation	Probability of exceedance	Reference
K-S d = 0.086, P > 0.20; Lilliefors P < 0.20	W = 0.969, P = 0.055	0.989	0.278	48%	[7]
K-Sd = 0.069, P > 0.20; Lilliefors P > 0.20	W = 0.9707, P = 0.066	0.766	0.196	11%	[8]
K-S d = 0.083, P > 0.20; Lilliefors P > 0.20	W = 0.970, P = 0.074	0.437	0.085	0%	[11]
—	—	—	—	—	[12]
K-S d = 0.069, P > 0.20; Lilliefors P > 0.20	W = 0.984, P = 0.421	0.910	0.232	35%	[13]
K-S d = 0.075, P > 0.20; Lilliefors P > 0.20	W = 0.971, P = 0.076	0.899	0.170	27%	[14]
K-S d = 0.067, P > 0.20; Lilliefors P > 0.20	W = 0.979, P = 0.2368	1.445	0.357	89%	[16–19]
K-S d = 0.074, P > 0.20; Lilliefors P > 0.20	W = 0.971, P = 0.096	1.232	0.314	77%	[20]
K-S d = 0.107, P > 0.20; Lilliefors P > 0.15	W = 0.970, P = 0.078	1.161	0.339	68%	[21]
K-S d = 0.081, P > 0.20; Lilliefors P > 0.20	W = 0.987, P = 0.648	1.381	0.321	88%	[15]

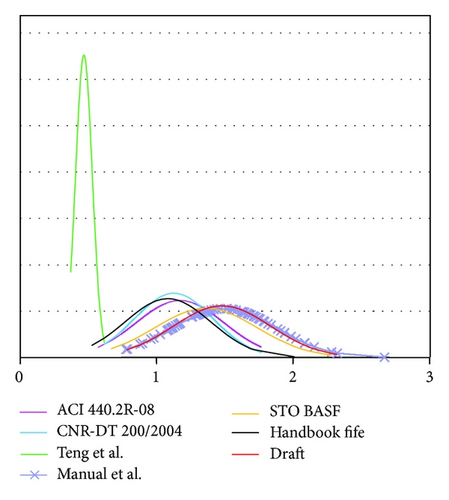
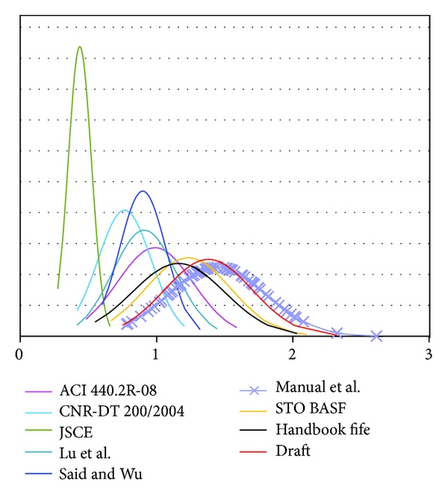
Analysis of Tables 2 and 3 and Figures 2 and 3 shows that all the Russians guideline give nonconservative results. A percentage of exceedance values vary from 68% to 89%. Among the foreign methods, Teng’s method was found to be the most reliable and the simplest. Note, however, that this method gives a too conservative results but does not provide a formula for estimating the design value of the debonding strains. We explain that too conservative debonding strains affect the efficiency of constructive solutions to strengthening. In other words, the debonding strains reducing leads to the necessity of increasing the area (width) of the FRP. Thus, we need to develop a formula for calculating the results which would have the greater efficiency and reliability required.

4. Proposed Analytical Formula

Next, based on Teng’s method, was proposeded a simple analytical formula for calculating the debonding strains, meeting the requirements of reliability and efficiency, and taking into account the traditional Russian values and notations for concrete strength. Characteristic value of the debonding strains should be calculated using (16), the design value according to (18). Consider

()

where R_b,n is characteristic value of compressive strength of concrete in compliance with Russian standard and k_b is the geometrical factor related to the width of the bonded plate and the width of the concrete member, using the formula (17). Consider

()

where R_b is design value of compressive strength of concrete in compliance with Russian standard.

Statistical analysis of data was performed to assess the reliability of the proposed method. The results of statistical analysis are shown in Table 4. In Figures 4 and 5 the normal distributions for x₁ and x₂ are shown.

Table 4. Results of statistical modeling for proposed analytical formula.

Reference

Kolmogorov-Smirnov

and Lilliefors tests

Shapiro-Wilk’s

W test

Mean,

theor/exp

Standard

deviation

Probability of

exceedance

x₁

K-S d = 0.065, P > 0.20;
Lilliefors P > 0.20

W = 0.969,
P = 0.066

0.732

0.145

<5%

x₂

K-S d = 0.065, P > 0.20;
Lilliefors P > 0.20

W = 0.969,
P = 0.066

0.687

0.136

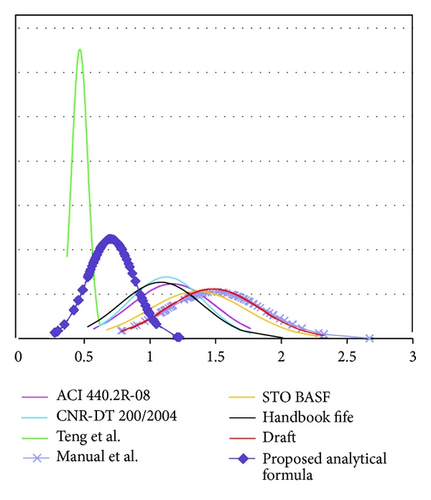
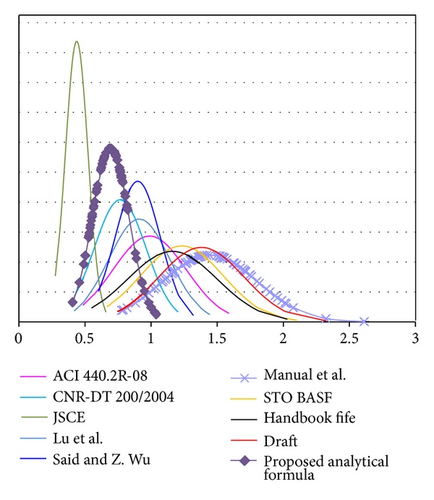
As can be seen from Table 4, the probability that the analytical model will overestimate the IC debonding failure is 5%. In other words, the probability of the characteristic value of the debonding strains calculated by the proposed model is 0.95. Similarly, it is shown that the probability of the design value of the debonding strains calculated by the proposed model is 0.99. So, these probabilities correspond to the Russian codes.

5. Conclusions

The authors carried out a review of existing methods for calculating the debonding strains of the FRP. Overview of domestic methods showed that they are built on the American approaches [7, 22] and thus have the same disadvantages as the American methods. The analysis of foreign experience makes it possible to determine the general form of the function for the debonding strains and set the desired values.

To verify and assess the reliability of the considered methods, the authors performed a comparison of the experimental and calculated data. Experimental data were collected from the published literature. These data were assembled into the experimental database, which included the 87 results. The assessment of the reliability of methods as the most simple and reliable method was adopted Teng’s method.

Based on Teng’s method, the authors proposed a simple analytical formula for calculating the debonding strains, meeting the requirements of reliability and efficiency, and taking into account the traditional Russian values and notations for concrete strength and lacking of the shortcomings of the original Teng’s method. Reliability analysis of the proposed model has shown that it meets the Russian codes requirements of reliability and efficiency and can be used in the design.

References

1 Esfahani M. R., Kianoush M. R., and Tajari A. R., Flexural behaviour of reinforced concrete beams strengthened by CFRP sheets, Engineering Structures. (2007) 29, no. 10, 2428–2444, 2-s2.0-34548233812, https://doi.org/10.1016/j.engstruct.2006.12.008.
Web of Science® Google Scholar
2 Ritchie P. A., Thomas D. A., Lu L.-W., and Connelly G. M., External reinforcement of concrete beams using fiber reinforced plastics, ACI Structural Journal. (1991) 88, no. 4, 490–500, 2-s2.0-0009811943.
Google Scholar
3 Saadatmanesh H. and Ehsani M. R., RC beams strengthened with GFRP plates. I. Experimental study, Journal of Structural Engineering. (1991) 117, no. 11, 3417–3433, 2-s2.0-0026253728.
Google Scholar
4 Triantafillou T. C. and Plevris N., Strengthening of RC beams with epoxy-bonded fibre-composite materials, Materials and Structures. (1992) 25, no. 4, 201–211, 2-s2.0-51249167749, https://doi.org/10.1007/BF02473064.
Google Scholar
5 Shahawy M. A., Arockiasamy M., Beitelman T., and Sowrirajan R., Reinforced concrete rectangular beams strengthened with CFRP laminates, Composites Part B. (1996) 27, no. 3-4, 225–233, 2-s2.0-0029706787, https://doi.org/10.1016/1359-8368(95)00044-5.
Google Scholar
6 Rahimi H. and Hutchinson A., Concrete beams strengthened with externally bonded FRP plates, Journal of Composites for Construction. (2001) 5, no. 1, 44–56, 2-s2.0-0035252786, https://doi.org/10.1061/(ASCE)1090-0268(2001)5:1(44).
Google Scholar
7 ACI 440. 2R-08, Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening of Concrete Structures, Michigan, American Concrete Institute, ACI Committee 440, p. 76, 2008.
Google Scholar
8 CNR-DT 200/2004, Guide for the Design and Construc-Tion of Externally Bonded FRP Systems for Strengthening Existing Structures—Materials, RC and PC Structures, Masonry Structures, 2004, Italian National Research Council, Rome, Italy.
Google Scholar
9 fib Bulletin 14. Externally bonded FRP reinforcement for RC structures, 130 p., 2001.
Google Scholar
10 TR55, Design Guidance for Strengthening Concrete Structures Using Fibre Composite Materials, The Concrete Society, UK, 72 p., 2004.
Google Scholar
11 JSCE, Recommendation for Upgrading of Concrete Structures with Use of Continuous Fiber Sheets, 2001, Japan Society of Civil Engineers, Tokyo, Japan, Concrete Engineering Series 41.
Google Scholar
12 Teng J. G., Smith S. T., Yao J., and Chen J. F., Intermediate crack-induced debonding in RC beams and slabs, Construction and Building Materials. (2003) 17, no. 6-7, 447–462, 2-s2.0-0141659633, https://doi.org/10.1016/S0950-0618(03)00043-6.
Google Scholar
13 Lu X. Z., Teng J. G., Ye L. P., and Jiang J. J., Intermediate crack debonding in FRP-strengthened RC beams: FE analysis and strength model, Journal of Composites for Construction. (2007) 11, no. 2, 161–174, 2-s2.0-33947306889, https://doi.org/10.1061/(ASCE)1090-0268(2007)11:2(161).
Google Scholar
14 Said H. and Wu Z., Evaluating and proposing models of predicting IC debonding failure, Journal of Composites for Construction. (2008) 12, no. 3, 284–299, 2-s2.0-44149109911, https://doi.org/10.1061/(ASCE)1090-0268(2008)12:3(284).
Google Scholar
15 Strengthening of reinforced concrete structures with composite materials, draft [Elektronnyy resurs]/OAO (NITs (Stroitelstvo)—NIIZhB imKholding), ZAO (KhK Kompozit), ZAO (BASF-Stroitelnyye sistemy), OAO (ROSNANO), OOO (EmSi Baukhemi)—Elektron. dan. (1 fayl)—Moskva, 2012, http://www.cstroy.ru/files/ntdoc/spusilzbk.pdf.
Google Scholar
16 Manual for strengthening reinforced concrete structures with composite materials. GUP (NIIZhB), OOO (Interakva). Moskva, 48 p., 2006.
Google Scholar
17 STO 34. 01. 01-2011, Usileniye proletnykh stroyeniy mostov materialami na osnove vysokoprochnykh uglerodnykh volokon. Upravleniye avtomobilnykh dorog administratsii volgogradskoy oblasti. Volgograd, 49 p., 2011.
Google Scholar
18 STO, 13613997-001-2011, Usileniye zhelezobetonnykh konstruktsiy kompozitnymi materialami firmy Sika, OAO (TsNIIPROMZDANIY). Moskva, 62 p., 2011.
Google Scholar
19 Rekomendatsii po raschetu usileniya zhelezobetonnykh konstruktsiy sistemoy vneshnego armirovaniya iz polimernykh kompozitov FibARM. GUP (NIIZhB). Moskva, 29 p., 2012.
Google Scholar
20 STO, 70386662-101-2012, Primeneniye sistemy vneshnego armirovaniya Mbrace dlya usileniya glavnykh balok zhelezobetonnykh proletnykh stroyeniy, zheleznodorozhnykh mostov. OOO (BASF Building Systems )—Moskva, 63 p., 2012.
Google Scholar
21 Shevtsov D.A. i dr. Posobiye po usileniyu zhelezobetonnykh konstruktsiy na izgib polimernymi kompozitnymi materialami kompanii Fyfe Ko. LLS, (k SP 52-101-2003) / Shevtsov D.A., Baturin S.A. M.: OAO (TsPP), 90 p., 2012.
Google Scholar
22 ACI 440.2R-02, Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures. Michigan, American Concrete Insti-tute, ACI Committee 440, 45 p., 2002.
Google Scholar
23 Bykov A. A., Tretyakova A. N., and Kalugin A. V., Evaluation of ultimate strain in frp at the onset of intermediate debonding failure for strengthening concrete structures, Vestnik Tomskogo Gosudarstvennogo Arkhitekturno-Stroitelnogo Universiteta. In press.
Google Scholar
24 Chen J. F. and Teng J. G., Anchorage strength models for FRP and steel plates bonded to concrete, Journal of Structural Engineering. (2001) 127, no. 7, 784–791, 2-s2.0-0035399279, https://doi.org/10.1061/(ASCE)0733-9445(2001)127:7(784).
Web of Science® Google Scholar
25 Lu X. Z., Teng J. G., Ye L. P., and Jiang J. J., Bond-slip models for FRP sheets/plates bonded to concrete, Engineering Structures. (2005) 27, no. 6, 920–937, 2-s2.0-18144382552, https://doi.org/10.1016/j.engstruct.2005.01.014.
Web of Science® Google Scholar
26 Reineck K.-H., Kuchma D. A., Kim K. S., and Marx S., Shear database for reinforced concrete members without shear reinforcement, ACI Structural Journal. (2003) 100, no. 2, 240–249, 2-s2.0-0038172615.
Google Scholar
27 EN, 1992-1-1. Eurocode 2: design of concrete structures—Part 1-1: General rules and rules for buildings.
Google Scholar

Citing Literature

All articles

New Model for Evaluation of FRP Debonding Strain for Russian Design Code

Abstract

1. Introduction