Abstract and Applied Analysis
Volume 2013, Issue 1 125089
Research Article
Open Access

Persistence and Nonpersistence of a Food Chain Model with Stochastic Perturbation

Haihong Li, 

Haihong Li

School of Mathematics, Jilin University, Changchun, Jilin 130024, China jlu.edu.cn

Department of Basic Courses, Air Force Aviation University, Changchun, Jilin 130022, China

Search for more papers by this author
Fuzhong Cong, 

Corresponding Author

Fuzhong Cong

School of Mathematics, Jilin University, Changchun, Jilin 130024, China jlu.edu.cn

Department of Basic Courses, Air Force Aviation University, Changchun, Jilin 130022, China

Search for more papers by this author
Daqing Jiang, 

Daqing Jiang

School of Mathematics, Northeast Normal University, Changchun, Jilin 130024, China nenu.edu.cn

Search for more papers by this author
Hongtu Hua, 

Hongtu Hua

Department of Basic Courses, Air Force Aviation University, Changchun, Jilin 130022, China

Search for more papers by this author
First published: 06 November 2013
https://doi.org/10.1155/2013/125089
Citations: 2
Academic Editor: Mark McKibben

Abstract

We analyze a three species predator-prey chain model with stochastic perturbation. First, we show that this system has a unique positive solution and its pth moment is bounded. Then, we deduce conditions that the system is persistent in time average. After that, conditions for the system going to be extinction in probability are established. At last, numerical simulations are carried out to support our results.

1. Introduction

Recently, the dynamical relationship between predator-prey has been one of the dominant themes in both ecology and mathematical ecology due to its universal importance. Especially, the predator-prey chain model is the typical representative. Thereby it significantly changed the biology, the understanding of the existence, and development of the basic law and has made the model become a research hot spot. One of the most famous models for population dynamics is the Lotka-Volterra predator-prey system which has received plenty of attention and has been studied extensively; see [1–4]. Specially persistence and extinction of this model are interesting topics.

The three species predator-prey chain model is described as follows:
()
where xi(t)  (i = 1,2, 3) denotes the population densities of the species at time t. The parameters a1, a2, a3, bii(i = 1,2, 3) are positive constants that stand for intrinsic growth rate, predator death rate of the second species, predator death rate of the third species, coefficient of internal competition, respectively. b21, b32 represent saturated rate of the second and the third predator and b12, b23 represent the decrement rate of predator to prey.

System (1) describes a three species predator-prey chain model in which the latter preys on the former. From a biological viewpoint, we not only require the positive solution of the system but also require its unexploded property in any finite time and stability.

We know that the global asymptotic stability of a positive equilibrium holds and is global stability if the following condition holds:
()
which could refer to [5]. However, population dynamics in the real world is inevitably affected by environmental noise (see, e.g., [6, 7]). Parameters involved in the system are not absolute constants, they always fluctuate around some average values. The deterministic models assume that parameters in the systems are deterministic irrespective of environmental fluctuations which impose some limitations in mathematical modeling of ecological systems. So we cannot omit the influence of the noise on the system. Recently many authors have discussed population systems subject to white noise (see, e.g., [8–15]). May (see, e.g., [16]) pointed out that due to continuous fluctuation in the environment, the birth rates, death rates, saturated rate, competition coefficients, and all other parameters involved in the model exhibit random fluctuation to some extent, and as a result the equilibrium population distribution never attains a steady value but fluctuates randomly around some average value. Sometimes, large amplitude fluctuation in population will lead to the extinction of certain species, which does not happen in deterministic models.

Therefore, Lotka-Volterra predator-prey chain models in random environments are becoming more and more popular. Ji et al. [14, 15] investigated the asymptotic behavior of the stochastic predator-prey system with perturbation. Liu and Chen introduced periodic constant impulsive immigration of predator into predator-prey system and gave conditions for the system to be extinct and permanence. Polansky [17] and Barra et al. [18] have given some special systems of their invariant distribution. After that, Gard [5] analysed that under some conditions the stochastic food chain model exists an invariant distribution. However, seldom people study the persistent and nonpersistent of the food chain model with stochastic perturbation.

In this paper, we introduce the white noise into the intrinsic growth rate of system (1), and suppose   (i = 1,2, 3); then we obtain the following stochastic system:
()
where Bi(t)(i = 1,2, 3) are independent white noises with Bi(0) = 0, (i = 1,2, 3) representing the intensities of the noise.

The aim of this paper is to discuss the long time behavior of system (3). We have mentioned that is the positive equilibrium of system (1). But, when it suffers stochastic perturbations, there is no positive equilibrium. Hence, it is impossible that the solution of system (3) will tend to a fixed point. In this paper, we show that system (3) is persistent in time average. Furthermore, under certain conditions, we prove that the population of system (3) will die out in probability which will not happen in deterministic system and could reveal that large white noise may lead to extinction.

The rest of this paper is organized as follows. In Section 2, we show that there is a unique nonnegative solution of system (3), and its pth moment is bounded. In Section 3, we show that system (3) is persistent in time average. While in Section 4, we consider three situations when the population of the system will be extinction. In Section 5, numerical simulations are carried out to support our results.

Throughout this paper, unless otherwise specified, let (Ω, {ℱt} t≥0, P) be a complete probability space with a filtration {ℱt} t≥0 satisfying the usual conditions (i.e., it is right continuous and ℱ0 contains all P-null sets). Let denote the positive cone of R3; namely, , .

2. Existence and Uniqueness of the Nonnegative Solution

To investigate the dynamical behavior, the first concern thing is whether the solution is global existence. Moreover, for a population model, whether the solution is nonnegative is also considered. Hence, in this section, we show that the solution of system (3) is global and nonnegative. As we have known, in order for a stochastic differential equation to have a unique global (i.e., no explosion at a finite time) solution with any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and local Lipschitz condition (see, e.g., [19]). It is easy to see that the coefficients of system (3) are locally Lipschitz continuous, so system (3) has a local solution. By Lyapunov analysis method, we show the global existence of this solution.

Theorem 1. For any given initial value , system (3) has a unique global positive solution x(t) = (x1(t), x2(t), x3(t)) for all t ≥ 0 with probability one.

Proof. It is clear that the coefficients of system (3) are locally Lipschitz continuous for the given initial value . So there is a unique local solution x(t) on t ∈ [0, τe), where τe is the explosion time (see, e.g., [19]). To show that this solution is global, we need to show that τe = ∞ a.s. Let m0 ≥ 1 be sufficiently large so that each component of x0 all lies within the interval [1/m0, m0]. For each integer m ≥ m0, define the stopping time:

()
Throughout this paper, we set inf ∅ = ∞ (as usual ∅ denotes the empty set). Clearly, τm is increasing as m → ∞. Set τ∞ = lim m→∞τm; then τ∞ ≤ τe a.s. If we can show that τ∞ = ∞ a.s., then τe = ∞ and a.s. for all t ≥ 0. In other words, to complete the proof all we need to show is that τ∞ = ∞ a.s. For if this statement is false, then there is a pair of constants T > 0 and ϵ ∈ (0,1) such that
()
Hence there is an integer m1 ≥ m0 such that
()
Define a C2-function by
()
the nonnegativity of this function can be seen from u − 1 − (1/2)log u ≥ 0, for all u > 0. Using Itô′s formula, we get
()
where
()
where is a constant. Therefore
()
which implies that
()
Set Ωm = {τm ≤ T} for m ≥ m1. By (6), we know P(Ωm) ≥ ϵ. Notice that for every ω ∈ Ωm, there is at least one of xi(τm, ω) equals either m or 1/m; then
()
It then follows from (11) that
()
where is the indicator function of Ωm. Letting m → ∞ leads to the contradiction that . So we must have τ∞ = ∞ a.s.

Theorem 2. Let x(t) = (x1(t), x2(t), and let x3(t)) be the solution of system (3) with any given initial value , then there exists a positive constant K(p) such that

()

Proof. Let y(t) = b32b21x1(t) + b32b12x2(t) + b23b12x3(t); then

()
and so
()
Note that
()
Then
()
Hence
()
Therefore, by comparison theorem, we get
()
Besides, note that E[yp(t)] is continuous; then there is a positive constant K(p) such that
()

3. Persistent in Time Average

There is no equilibrium of system (3). Hence we cannot show the permanence of the system by proving the stability of the positive equilibrium as the deterministic system. In this section we first show that this system is persistent in mean. Before we give the result, we should do some prepared work.

L. S. Chen and J. Chen in [20] proposed the definition of persistence in mean for the deterministic system. Here, we also use this definition for the stochastic system.

Definition 3. System (3) is said to be persistent in mean, if

()

Lemma 4 (see [21], Lemma 17.)Let f ∈ C([0, +∞) × Ω, (0, +∞)) and F ∈ C([0, +∞) × Ω, R). If there exist positive constants λ0, λ, such that

()
and lim t→∞(F(t)/t) = 0a.s., then
()

From Lemma 4, it is easy to see that we could get Lemmas 5 and 6 with the same method.

Lemma 5. Let f ∈ C([0, +∞) × Ω, (0, +∞)) and F ∈ C([0, +∞) × Ω, R). If there exist positive constants λ0, λ, such that

()
and lim t→∞(F(t)/t) = 0a.s., then
()

Lemma 6. Let f ∈ C([0, +∞) × Ω, (0, +∞)) and F ∈ C([0, +∞) × Ω, R). If there exist positive constants λ0, λ, such that

()
and lim t→∞(F(t)/t) = 0a.s., then
()

From the stochastic comparison theorem [11], it is easy to get the following result.

Lemma 7. Let be a solution of system (3) with x(0) = (x1(0), x2(0), x3(0)). Then one has

()
that is,
()
where
()
Φi(t) is solutions of the following stochastic differential equations:
()

Assumption 8. Consider

()

Lemma 9. If Assumption 8 is satisfied, the solution Φ(t) of system (32) with any initial value has the following property:

()
where
()

Proof. From the result in [14] and Assumption 8 being satisfied, we know

()
Besides, according to Itô′s formula, the second population of system (32) is changed into
()
It then follows
()
With Lemma 6 and Assumption 8, we could get
()
Let (38) divide t, and t → ∞, together with (36) and (39), consequently
()
Similarly, according to Itô′s formula, the third population of system (25) is changed into
()
it then follows
()

From this, together with Lemmas 7 and 9, the following result is obviously true.

Theorem 10. If Assumption 8 is satisfied, the solution x(t) of system (3) with any initial value has the following property:

()

Above all, we could get.

Theorem 11. If Assumption 8 is satisfied, the the solution x(t) of system (3) with any initial value has the following property:

()
where is the only nonnegative solution of the following equation:
()

Proof. From system (3), such that

()
Let c1 = b21, c2 = b11, and c3 = (b11b22 + b12b21)/b32, together with Assumption 8, we know
()
hence
()
According to Theorem 10, where
()
and lim t→∞(Bi(t)/t) = 0, i = 1,2, 3,
()
where is the only nonnegative solution of the following equation when Assumption 8 is satisfied:
()

4. Nonpersistence

In this section, we show the situation when the population of system (3) will be extinction in three cases.

Case 1 (r1 < 0). According to Itô′s formula, the first population of system (25) is changed into

()
If r1 < 0, we could get
()
From the stochastic comparison theorem, we have
()
hence
()
From the second population of system (25), we have
()
similarly
()

Case 2 (r1 > 0, r1 − (b11/b21)r2 < 0). It is clear that from the proof section of Case 1, we get

()
hence
()
Similarly
()
thus,
()

Above all, and from the conclusion in [22], we could easily know that the distribution of x1(t) converges weekly to the probability measure with density:
()
where and
()

Case 3 (r1 − (b11/b21)r2 − ((b11b22 + b12b21)/b21b32)r3 < 0). It is clear that

()
Since c1 = b21, c2 = b11, c3 = (b11b22 + b12b21)/b32, we get
()
Moreover,
()
And lim t→∞(Bi(t)/t) = 0, i = 1,2, 3, implies
()
then
()
Therefore, by the above arguments, we get the following conclusion.

Theorem 12. Let x(t) be the solution of system (3) with any initial value . Then

(1) if r1 < 0, then

()

(2) if r1 > 0, r1 − (b11/b21)r2 < 0, then

()
and the distribution of x1(t) converges weekly to the probability measure with density:
()
where and
()

(3) if r1 − (b11/b21)r2 − ((b11b22 + b12b21)/b21b32)r3 < 0, then

()
where c1 = b21, c2 = b11, and c3 = (b11b22 + b12b21)/b32.

5. Numerical Simulation

In this section, we give out the numerical experiment to support our results. Consider
()
By the Milstein method in [23], we have the difference equation:
()
where ϵ1,k, ϵ2,k, and ϵ3,k, i = 1,2, 3, are the Gaussian random variables N(0,1), , and , i = 2,3. Choosing , and suitable parameters, by Matlab, we get Figures 1, 2, and 3.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The solution of system (1) and system (3) with (x1(0), x2(0), x3(0)) = (1,0.8,0.5), a1 = 0.3, a2 = 0.4, a3 = 0.1, b11 = 0.1, b12 = 0.1, b21 = 0.6, b22 = 0.6, b23 = 0.6, b32 = 0.8, and b33 = 0.6. The red lines represent the solution of system (1), while the blue lines represent the solution of system (3) with σ1 = 0.02, σ2 = 0.01, and σ3 = 0.01.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Two of the species will die out in probability. The red lines represent the solution of system (1), while the blue lines represent the solution of system (3) with (x1(0), x2(0), x3(0)) = (1,0.8,0.5), a1 = 0.4, a2 = 0.4, a3 = 0.1, b11 = 0.1, b12 = 0.1, b21 = 0.6, b22 = 0.6, b23 = 0.6, b32 = 0.8, and b33 = 0.6. The red lines represent the solution of system (1), while the blue lines represent the solution of system (3) with σ1 = 0.02, σ2 = 3, and σ3 = 0.01.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
One of the species or both species will die out in probability. The red lines represent the solution of system (1), while the blue lines represent the solution of system (3) with (x1(0), x2(0), x3(0)) = (1,0.8,0.5), a1 = −0.1, a2 = 0.4, a3 = 0.1, b11 = 0.1, b12 = 0.1, b21 = 0.6, b22 = 0.6, b23 = 0.6, b32 = 0.8, and b33 = 0.6. The red lines represent the solution of system (1), while the blue lines represent the solution of system (3) with σ1 = 0.02, σ2 = 3, and σ3 = 0.01.

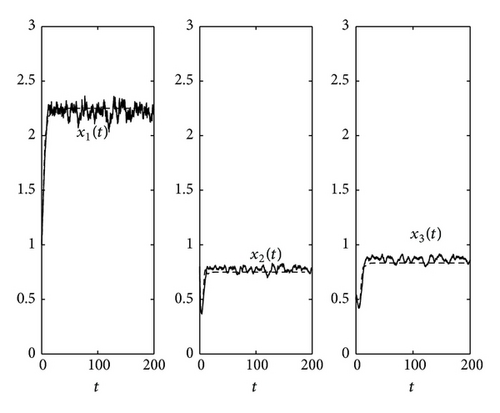
In Figure 1, when the noise is small, choosing parameters satisfying the condition of Theorem 10, the solution of system (3) will persist in time average.

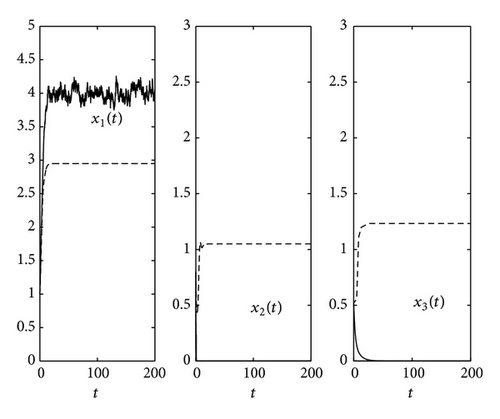
In Figure 2, we observe case (3) in Theorem 12 and choose parameters r1 > 0, r1 − (b11/b21)r2 < 0. As Theorem 12 indicated that two predators will die out in probability. The prey solution of system (3) will persist in time average.

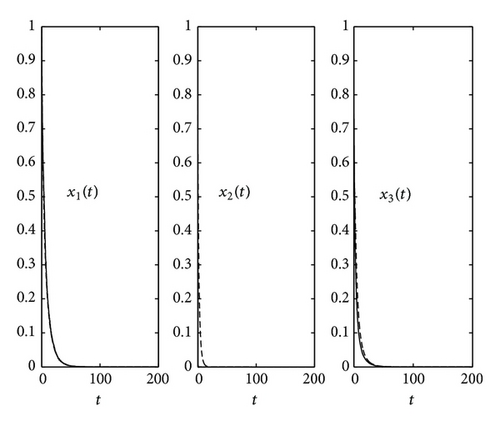
In Figure 3, we observe case (1) in Theorem 12 and choose parameters r1 < 0. As Theorem 12 indicated that not only predators but also prey will die out in probability when the noise of the prey is large, and it does not happen in the deterministic system.

Acknowledgments

The work was supported by the Ministry of Education of China (no. 109051), the Ph.D. Programs Foundation of Ministry of China (no. 200918), and NSFC of China (no. 11371085), Natural Science Foundation of Jilin Province of China (no. 201115133).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.