Abstract and Applied Analysis
Volume 2013, Issue 1 105724
Research Article
Open Access

Mechanism of Stochastic Resonance in a Quorum Sensing Network Regulated by Small RNAs

Ya-nan Zhu, 

Ya-nan Zhu

Institute of Applied Mathematics, Xuchang University, Xuchang, Henan 461000, China xcu.edu.cn

Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author
Jianwei Shen, 

Corresponding Author

Jianwei Shen

Institute of Applied Mathematics, Xuchang University, Xuchang, Henan 461000, China xcu.edu.cn

Search for more papers by this author
Yong Xu, 

Yong Xu

Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author
First published: 24 November 2013
https://doi.org/10.1155/2013/105724
Citations: 3
Academic Editor: Jinde Cao

Abstract

Bacterial quorum sensing (QS) is an important process of cell communication and more and more attention is paid to it. Moreover, the noises are ubiquitous in nature and often play positive role. In this paper, we investigate how the noise enhances the QS though the stochastic resonance (SR) and explain the mechanism of SR in this quorum sensing network. In addition, we also discuss the interaction between the small RNA and the other genes in this network and discover the biological importance.

1. Introduction

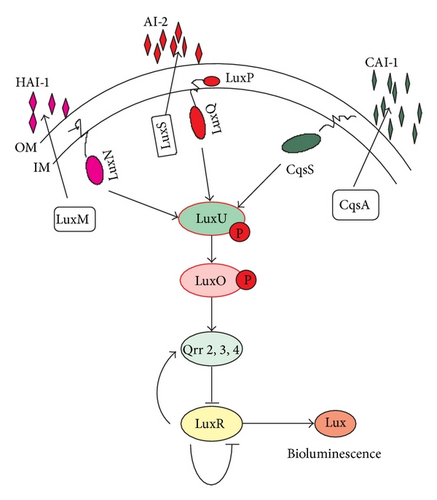
In each cell, the survival of bacteria depends mainly on the regulatory networks involved in quorum sensing, which is a mechanism of cell communication that enable bacteria to track population density by secreting and detecting extracellular signaling molecules called autoinducers (AIs) [1, 2]. QS can regulate the concentration of AIs and alter the expression of genes to transmit information and carry out task. Recently, the experiments [3, 4] show that the small RNAs play an important role in QS network of the bacterium Vibrio harveyi and indicate that there is a feedback loop between small RNAs and QS master regulatory protein.

In order to investigate qualitatively the QS, we hope to model the network by the use of mathematical tool. Shen [5] constructs a mathematical model according to Michaelis-Menten kinetics and mass action law and shows the oscillatory dynamics of the QS network regulated by small RNA and obtains some theoretical results. As we know, there are noises when the genes interact in cell, and the movement of genes abides by Gaussian distribution. In this paper, we will investigate how the noise enhances the QS though the stochastic resonance (SR) and explain the mechanism of SR in this quorum sensing network. Stochastic resonance is said to be observed when increases in levels of unpredictable fluctuations take place. for example, random noises cause an increase in the metric of the quality of signal transmission or detection performance rather than a decrease.

Hobert [6, 7] discussed common principles and conceptual differences between transcription factor and microRNA regarding how these factors control gene expression. Shimoni et al. [8], showed quantitatively that regulation by sRNA is advantageous when fast responses to external signals are needed, which is consistent with experimental data about its involvement in stress responses.

Moreover, the studies show that noises often play the constructive role, enhancing the response of a nonlinear system and emerging the type of stochastic resonance (SR). SR can be realized in a wide variety of systems, including monostable systems [9], excitable systems [10], and bistable-well systems [11, 12]. The effect of SR has equally been examined in physical systems [13, 14] and chemical systems [15, 16], as well as biological systems [17, 18]. These SR phenomena are typically driven by periodic forces or noise signals. Especially, Hou and Xin [19] found that noises can induce circadian oscillations, when the corresponding deterministic system does not oscillate; that is, stochastic resonance occurs when circadian oscillation undergoes to maximum at a certain noise level. However, it is worth noting that noises can enhance the performance of oscillation when the corresponding deterministic system does oscillate, which suggests that stochastic resonance will occur for a particular noise intensity. Here, we also consider the QS network driven by noises.

The rest of the paper is organized as follows. In Section 2, we give the model description. In Section 3, we describe the method of how to investigate the noises on this network. In Section 4, we give some results and discuss the dynamics and the mechanism of SR on QS network.

2. Model Description

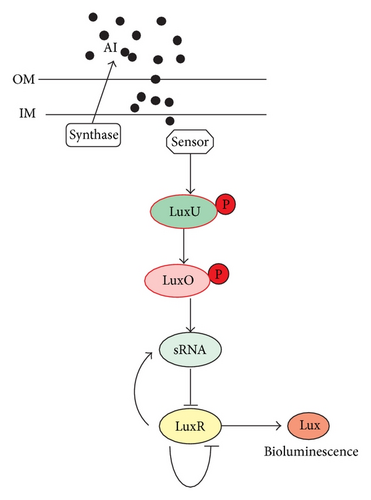
Bacteria quorum sensing regulated by small RNA in Vibrio harveyi was descripted by Miller an Bassler [1], Waters and Bassler [2]; they descripted the network as in Figure 1.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Schematic diagram showing the gene regulation mediated by sRNA with a negative feedback loop. (a) Original model; (b) abstract model.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Schematic diagram showing the gene regulation mediated by sRNA with a negative feedback loop. (a) Original model; (b) abstract model.
For the quorum sensing network in Vibrio harveyi, the phosphorylation of regulator protein LuxO can be controlled by the interaction between AIs and sensors. At negligible concentrations of AIs, that is, at low cell density (LCD), these sensors act as kinases that transfer phosphate through LuxU to LuxO [3, 4]. LuxO-P activates the expression of genes encoding small RNAs which in turn posttranscriptionally repress the QS master regulatory protein LuxR. At the high cell density (HCD), AIs accumulate and bind to their cognate sensors and the sensors act as phosphatases, reversing the phosphate flow through the QS circuit. This results in dephosphorylation and inactivation of LuxO, so that the expression of genes encoding the small RNAs is terminated. To understand the dynamics of this network, Shen [5] abstracted Figure 1(b) from Figure 1(a) and investigated the dynamics of the quorum sensing network regulated by Small RNAs for some fixed parameters and found that Hopf bifurcation occurred in this system when control parameter undergo a critical value τ0. However, we know that signal recognized by living organisms is often noisy, and it is not typically ignored. To further characterize the dynamics of quorum sensing network, it is essential to consider the effect of noise on Quorum Sensing network [5]. When noise is taken into account, we can describe the dynamics of the model using stochastic differential equations as follows:
()
where
()
In the above equations, [LuxM], [AI], [LuxU], [sRNA], [mRNA], [protein], and [Lux] represent the concentrations of LuxM, AI, LuxUp, sRNA, mRNA, protein, and Lux, respectively. Sk represents sensor corresponding to the kinase state and Sp represents the sensor corresponding to the phosphatase state. LuxO is a kind of regulator protein. LuxO represents phosphorylated LuxOp. k1 ~ k6 represent the reaction rate and the k−1 ~ k−3, k−5 ~ k−6 represent the dissociation constant. k7 ~ k10 and δ1 ~ δ2 are the basal rate of transcription in the absence of transcription. d1 ~ d7 represent the degradation rate. r is a rate for small RNA base pairs with the target mRNA. m and n are Hill coefficients. τ1 and τ2 are the time delays. The noise ξ(t) is assumed as Gaussian noise with zero mean and delta-correlated: 〈ξ(t)ξ(t′)〉 = δ(t − t′); 〈·〉 denote an ensemble average and D is noise intensity.

3. Methods

Quorum sensing makes the concentration of protein circulate from HCD to LCD and transmits the information. In real world, the noises are ubiquitous and play an important role; they can increase the periodical oscillation from HCD to LCD and emerge the phenomena of stochastic resonance. As we all know, the measures characterizing SR are present widely in nonlinear system, including amplification factor, signal-to-noise ratio, the degrees of coherence and of order. For example, Fauve and Heslot used SNR (signal-to-noise ratio) as a measure for characterizing SR phenomenon in the Schmitt trigger system [20] subjected to a weak periodic signal. Jung and Hänggi described SR phenomenon using the measure of spectral power amplification (SPA) in the standard double-well system [11] subjected to periodic forces and noise signal. Although these measures showed some differences in definition, they measure have a common feature which undergo to the maximum for a certain optimal noise intensity. Here we adopt SNR as a method for describing SR phenomenon in the context of a Quorum Sensing network with time delay regulated by small RNAs, where SNR [21] is defined as the ratio between the peak of the power spectrum of a signal and the width of frequency corresponding to height h1 = e−1/2*peak. The formula of SNR is as follows:
()
where H is the maximum of the power spectrum of a signal, ωp is the internal signal frequency, and Δω is the width of frequency corresponding to height h1 = e−1/2*H. Additionally, the spectral estimate [22] at a given frequency for a single discrete signal series xt is
()
In the above equation, cxx(k) is the autocovariance function evaluated at the lag k, Δ is the distance between adjacent time series values, L is the length of signal series, and f is the frequency. The w(k) is the window function; here, we adopt Welch window [23] as window function. The autoamplitude spectral estimate (power spectrum) is defined as P(f) = |Cxx(f)|2. In the following, we will make use of the above method to discuss the QS network.

4. Results and Discussion

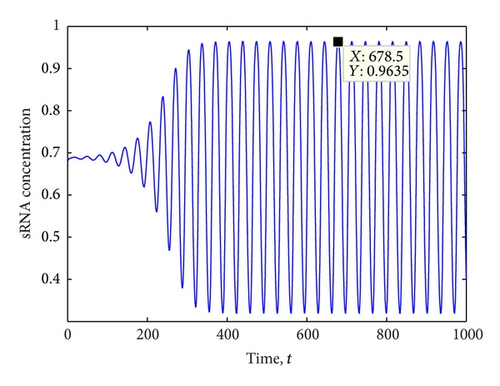
In the previous work, we know that there are periodical oscillations when control parameter τ(τ1 + τ2) is larger than critical value. Now, we mainly focus on the effect of noise when τ is larger than threshold value; that is, the corresponding deterministic system is oscillatory. In order to investigate the effect of noise, firstly, we integrate the corresponding deterministic system and stochastic differential system (1) for control parameter τ = 10.5 which is on the right of critical value. Figure 2 shows the tendency for time history diagram of small RNA concentration when D = 0. These oscillations of small RNA caused by different noise levels are presented in Figure 3. Here, the parameter values that remain unchanged during simulation are as follows: a1 = 1, s0 = 2, u0 = 2, k = 0.8, m = 2, n = 2, O0 = 2, r = 1, k0 = 0.8, k1 = 0.2, k4 = 0.3, k5 = 0.3, k6 = 1, k7 = 0.5, k8 = 2, k9 = 1, k10 = 1, d1 = 0.5, d2 = 0.6, d3 = 0.5, d4 = 0.3, d5 = 0.2, d6 = 0.1, a1 = 1, d7 = 0.8, δ1 = 1, δ2 = 1.1, τ1 = 3.5, and τ2 = 7.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Time history diagram of small RNA concentration when D = 0.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The dynamics of system (1) for different noise intensities: From bottom to top, D = 0.8, D = 0.05,   and D = 0.01.

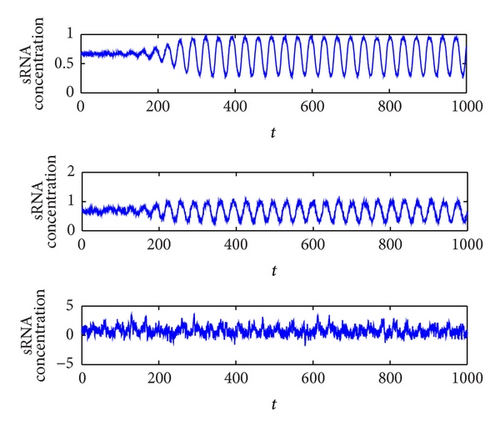
Comparing Figures 2 and 3, we clearly see that the periodical oscillation of small RNA is not explicitly improved when small noise intensity is added in the system (1), while the periodic oscillation of small RNA is almost completely disturbed by strong noise amplitude; that is, the strong noise-induced oscillations appear to be rather irregular. However, we surprisingly find that the periodical oscillation of small RNA is largely improved at a particular noise intensity. Meanwhile, we can also illustrate the above results in terms of power spectrum.

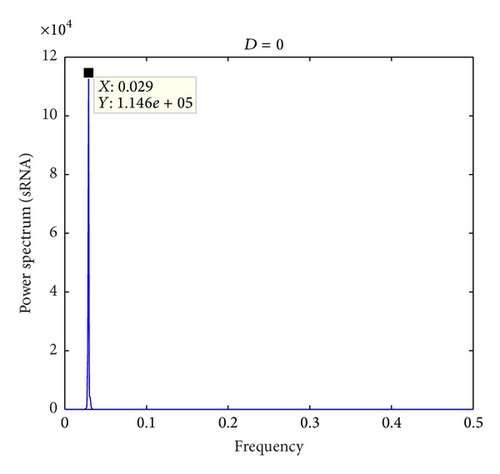
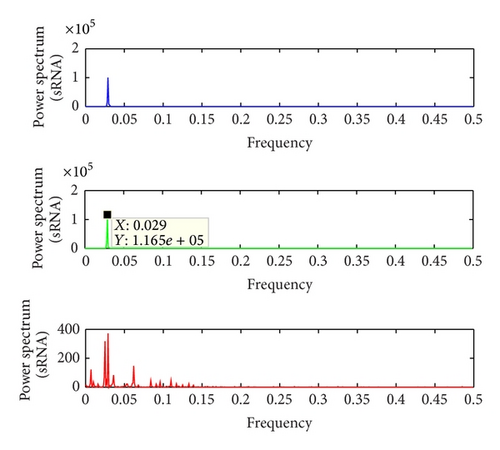
We know that the frequency of period oscillation is about 0.029 as shown in Figure 2. The corresponding power spectrum performs an obvious peak in the foundational frequency, which can be seen in Figure 4. Additionally, the power spectrum diagrams of small RNA that caused different noise amplitudes are depicted in Figure 5. It is easy to find that the peak values at the internal signal frequency (0.029) for both the small and large noise amplitudes are smaller than of the corresponding deterministic system. However, the peak value in the second diagram in Figure 5 is larger than that in the second diagram in Figure 4, showing that the oscillation amplitude of small RNA is improved to a large extent, which suggests that explicit internal stochastic resonance occurs at a certain optimal noise intensity. This means that the amplitude of these peaks will increase up to a certain critical noise level when the noise intensity is increased. After this point, information on the output signal will degrade, so the performance of quorum sensing on the network will be increased at the optimized noise and will be propitious to communicate between intracelluar and extracelluar.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The power spectrum of small RNA presented in Figure 2.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The power spectrum of small RNA presented in Figure 3.

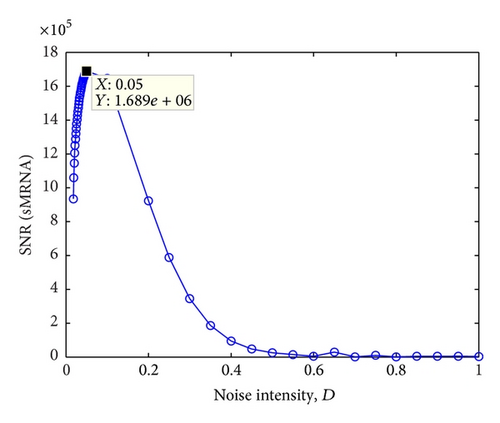
Finally, to qualitatively characterize stochastic resonance, here, we use SNR defined in Section 3 to illustrate this phenomenon. The SNR versus noise intensity is presented in Figure 6. It is clear to show that the rapid rise of SNR to a peak with varying noise amplitude, which implies that explicit internal stochastic resonance appears at the peak value. This means that the performance of such sustained oscillation undergoes the maximum with the increment of internal noise and reaches the optimal condition at the maximum of peak. Previous studies on biological networks often view noise as a nuisance, so the regulatory mechanisms need to show robustness or resistance to random noise. In our work, we show that noise can play constructive roles via SR. It was well known that many biological systems can take advantage of the benefits of noise for nonlinear transmission and amplification of feeble information and increase the information communication via quorum sensing in Vibrio Harveyi.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
SNR as functions of the noise amplitude D.

5. Conclusions

In this work, we only focus on the dynamics of small RNA and study the influence of noises on a Quorum Sensing network regulated by small RNAs in Vibrio Harveyi. We demonstrate that noise can enhance the performance of oscillation when the corresponding deterministic system stays in the oscillatory region; that is, explicit internal stochastic resonance appears at an optimal noise intensity. Such phenomenon implies that explicit internal stochastic resonance might be widely appeared in biological regulatory networks and can speed up the information between intracellular and extracellular in the quorum sensing network and also improve the performance of small RNAs which regulate the quorum sensing network.

Conflict of Interests

The authors declare that there is no conflict of interests.

    Acknowledgments

    This work is supported by the National Natural Science Foundation of China (11272277), the Program for New Century Excellent Talents in University (NCET-10-0238), the Key Project of Chinese Ministry of Education (211105), the Innovation Scientists and Technicians Troop Construction Projects of Henan Province (134100510013), and the Innovative Research Team in University of Henan Province (13IRTSTHN019).

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.