For an internal conductivity image, magnetic resonance electrical impedance tomography (MREIT) injects an electric current into an object and measures the induced magnetic flux density, which appears in the phase part of the acquired MR image data. To maximize signal intensity, the injected current nonlinear encoding (ICNE) method extends the duration of the current injection until the end of the MR data reading. It disturbs the usual linear encoding of the MR k-space data used in the inverse Fourier transform. In this study, we estimate the magnetic flux density, which is recoverable from nonlinearly encoded MR k-space data by applying a Newton method.

1. Introduction

An electric current injected into an electrically conducting object, such as the human body, induces an internal distribution of the magnetic flux density B = (B_x, B_y, B_z). Magnetic resonance electrical impedance tomography (MREIT) visualizes the internal conductivity distribution from the z-component B_z of B which can be measured in practice using an MRI scanner. This technique was originally proposed by Joy et al. in 1989 [1]; since then, several researchers [2–10] have investigated and further developed MREIT as well as magnetic resonance current density image (MRCDI), which has similar modalities [11–13].

The magnetic flux density B_z induced by injecting current through the electrodes attached on the surface of a conducting object Ω accumulates its signals in the phase parts of acquired MR image data. The conventional current-injection method [1, 8] injects the current during time T_c, between the end of the first RF pulse and the beginning of the reading gradient, in order to ensure gradient linearity.

Since the signal-to-noise ratio (SNR) of the MR magnitude depends on the echo time T_E, it is impossible to increase both T_c and the SNR of the MR magnitude simultaneously in order to reduce noise effects. As an attempt to reduce the noise level, the injected current nonlinear encoding (ICNE) method was developed in 2007 [14, 15]; it extends the duration of the injection current until the end of a reading gradient in order to maximize the signal intensity of B_z. Then, it disturbs the usual linear encoding of MR k-space data used in the inverse Fourier transform.

For example, the one-dimensional inverse problem in the conventional acquisition method is to find the unknown discrete magnetic flux density b_l, l = 0, …, N − 1 from the N × N matrix A satisfying the following:

()

where T_c is a constant and

are known quantities that can be measured. By an inverse Fourier transform ℱ⁻¹, the first equation in (1.1) becomes

()

The unknown data b_l is simply recovered from (1.2). In the ICNE method, however, the matrix A is perturbed to

. Then, it becomes a system of nonlinear equations for unknown b_l data, where the conventional inverse Fourier transform is no longer applicable.

In this paper, we prove a unique determination of the magnetic flux density from measured MR signal obtained by the ICNE acquisition method. Secondly, applying a Newton method, we suggest a bound of l₂-norm for recoverable magnetic flux density from nonlinearly encoded MR k-space data. Numerical experiments show the feasibility of the proposed method.

2. ICNE Method and Invertibility

For a standard spin echo pulse sequence in MR imaging, the k-space MR signal

()

is measured, where ρ denotes a positive spin density of the imaging slice and δ any systematic phase artifact [16]. From the signal S in (2.1), by applying the conventional inverse Fourier transform, we can obtain

()

and the clinical MR image data ρ = |ρ⁰|.

In MREIT, we inject the current I through the electrodes attached on the three-dimensional conducting object Ω, having conductivity distribution σ. The injection current I produces the internal current density J and the magnetic flux density B = (B_x, B_y, B_z) in Ω, satisfying the Ampère and Biot-Savart laws. Since an MRI scanner measures only the main magnetic field direction component of B, the z-component B_z, we focus on the problem of measuring B_z(x, y) = B_z(x, y, z₀), where z₀ is the center of the selected imaging slice. Since MREIT is a methodology for reconstructing the internal conductivity σ from B_z data, it is important to measure B_z more precisely.

2.1. Conventional B_z Acquisition

For a conventional B_z acquisition, current is not injected during T_s of the MR data acquisition, ADC as shown in Figure 1. In this case, the induced magnetic flux density B_z provides additional dephasing of spins, and, consequently, extra phase is accumulated during the total injection time T_c. Then, the measured k-space data for the injection current I can be represented as follows:

()

where γ = 26.75 × 10⁷ rad/T·s is the gyromagnetic ratio of hydrogen.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Conventional and ICNE current injections in a spin echo pulse sequence.

From the measured S and S^I in (2.1) and (2.3), by applying an inverse Fourier transform, we obtain ρ⁰ in (2.2) and

()

Then, the magnetic flux density B_z is precisely computed as

()

where α and β are the imaginary and real parts of ρ^I/ρ⁰, respectively.

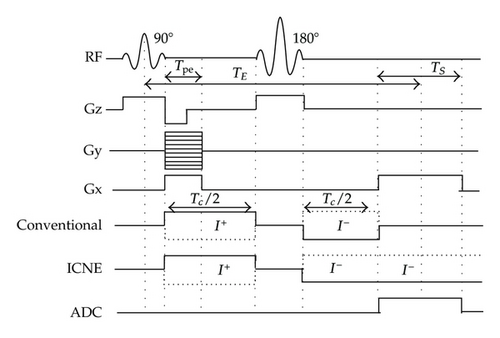
2.2. ICNE B_z Acquisition

In the ICNE B_z acquisition, in order to improve the SNR of B_z, we prolong the current injection time T_c until the end of the MR data acquisition, as shown in Figure 1. Then, since the induced B_z disturbs the linearity of the reading gradient, the measured k-space data has lost the linear encoding characteristic as

()

where G is a constant that denotes the strength of the magnetic reading gradient. The inverse problem arising in the ICNE method is to recover B_z(x, y) from ρ⁰(x, y) obtained in (2.2) and the measured signal S^C(k_x, k_y) in (2.6).

Although the inversion is not uniquely solvable for B_z(x, y) in general, we can uniquely determine B_z(x, y) by assuming that φ(x): = x + B_z(x, y)/G is monotone increasing in the following theorem.

Theorem 2.1. Let ρ(x, y) have a finite support Ω. If B_z(x, y) is sufficiently small to guarantee that φ(x) = x + B_z(x, y)/G is monotone increasing so that φ^′(x) > 0 for each y, then B_z(x, y) is uniquely recovered in Ω from ρ⁰(x, y) in (2.2) and S^C(k_x, k_y) in (2.6).

Proof. We note that the linear encoding characteristic in the k_y-variable remains unperturbed in (2.6). Thus, by one-dimensional inverse Fourier transform, S^C in (2.6) is reduced to in the (k_x, y)-hybrid space as the following:

()

Then, the ICNE inverse problem suffices to consider the x-directional inversion of B_z(x, y) from ρ⁰(x, y) in (2.2) and

in (2.7) for each fixed y.

By change of variables with φ(x), (2.7) is changed into

()

From (2.8), by inverse Fourier transform for the φ-variable, φ satisfies

()

where Φ is a function defined with the given

()

The relation (2.9) gives us the simple ordinary differential equation as follows:

()

Since ρ has a finite support, for each y, we can define

()

If φ(x₀) < β, then φ(x₀ + ϵ) < β for a sufficiently small ϵ > 0. It contradicts (2.11), since it implies that

()

By the same argument, the reverse inequality is not possible. Thus, we have

()

By separation of variables, (2.11) and (2.14) lead us to

()

For any given x, φ(x) is uniquely determined from (2.15). It completes the proof.

Remark 2.2. In Theorem 2.1, we assume that φ^′(x) = 1 + (1/G)(∂B_z(x, y)/∂x) > 0. The magnetic flux density B_z is smooth and its intensity is 10⁻⁷ ~ 10⁻⁸ T in practical experimental environments. Furthermore, the usual range of the reading gradient G is 10⁻³ ~ 10⁻⁴ T/m. Thus, the assumption of φ^′(x) > 0 is not severe in Theorem 2.1.

3. Discrete ICNE Inverse Problem

In a practical MRI scanner, the MR k-space data in (2.1), (2.3), and (2.6) are acquired by finite sampling with a dwell time dt. If N is the reading time T_s divided by dt, we have the following N × N discrete signals with dimensionless variables instead of those in (2.6):

()

for a constant M > 0.

The discrete ICNE inverse problem is to recover B_z(n, m) from (3.1) with known a priori ρ(n, m)e^iδ(n,m) and the measured signal

, where n, m, k, l = 0,1, …, N − 1. By discrete inverse Fourier transform for l, (3.1) can be suppressed into

()

For each fixed m, let s(k), ρ_n, and b_n denote

, and B_z(n, m), respectively. Then, the discrete ICNE inversion problem is a system of N nonlinear equations for N unknowns, b₀, b₁, …, b_N−1 such that

()

where M > 0 and s(k), ρ_n ∈ ℂ, n, k = 0,1, …, N − 1 are known.

In the rest of the paper, we assume that N is even and k, n = 0,1, …, N − 1 denote the row and column numbers, respectively. A matrix whose (k, n) entry is M_kn is represented by

()

For a vector x = (x₀, x₁, …, x_N−1) ^t,

denotes a Vandermonde matrix as

()

3.1. Newton Iterations

Define a function F = (F₀, F₁, …, F_N−1) ^t by

()

for x = (x₀, x₁, …, x_N−1) ^t ∈ ℝ^N. The discrete ICNE inverse problem is to find the zero of F for s(k) given in (3.3).

The Jacobian matrix DF(x) is composed of four parts as

()

where

are diagonal matrices such that

()

Newton iterations to find the zero of F are as the following:

()

with an initial x⁰ and the iterates

The previous method in [14, 15] was based on the Taylor approximation, but as a coincidental result, it can be interpreted as the first Newton iterate x¹ in (3.9) with x⁰ = 0.

3.2. Convergence of Newton Iterations

Let

, and ρ_max = max _n | ρ_n | , ρ_min = min _n | ρ_n|. If

()

the Jacobian DF(b) in (3.7) is invertible, since the Vandermonde matrix V(b) in (3.5) is based on the N distinct points. Thus, the Newton iterations in (3.9) converge to b for an initial x⁰ which is sufficiently close to b [17].

The following theorem suggests a condition for b in which the Newton iterations in (3.9) converge to b with the trivial initial guess 0 = (0,0, …, 0) ^t. The proof is based on the Theorem 6.14 in [17], which states a sufficient condition for the convergence of Newton iterations that

()

where

and β, γ are the respective bounds of

()

Theorem 3.1. Let s(k) in (3.6) be made through (3.3) from b such that

()

Then, starting with x⁰ = 0, the Newton iterations in (3.9) are well defined and converge to b. One also has the following quadratic error estimate:

()

As a consequence, the zero of F satisfying (3.13) is unique.

Proof. Let . The condition (3.13) and Lemma 3.3 lead us to

()

If ∥x∥_∞ ≤ 2α, we have from (3.13), (3.15), and Lemma 3.5, the following:

()

By (3.7), (3.16) implies that

()

For two constants in (3.17) and (3.21), let

()

From (3.15) and the condition (3.13), we have

()

Then, with the aid of the Theorem 6.14 in [17], F has a unique zero x^⋆ in the ball

()

and the Newton iterations in (3.9) converge to x^⋆ with x⁰ = 0. Since b is a zero of F contained in B from (3.15), we have x^⋆ = b. The quadratic error estimate in (3.14) also comes from the same theorem in [17].

Lemma 3.2. If x, y ∈ ℝ^N, then

()

Proof. From (3.7), we expand

()

Since |e^iθ − 1 | = 2 | sin (θ/2)|, we have for each k,

()

We can combine (3.22), (3.23a), (3.23b), and (3.23c) into (3.21).

Lemma 3.3. For the trivial initial x⁰ = 0, one has

()

Proof. Since

()

we can represent F(0) as

()

Thus, we expand

()

where

()

From Lemma 3.4, we estimate that

()

Since V(0) is the matrix of the discrete Fourier transform, we have

()

which implies that

()

The proof is completed by (3.27a), (3.27b), (3.27c), (3.27d), (3.27e), (3.29), and (3.31).

Lemma 3.4. If θ is real, then

()

Proof. If |θ | ≤ 3, we have (3.32) since the series in the following expansion is alternating.

()

If |θ | > 3, we obtain (3.32) from

()

3.3. Norm of Inverse of Vandermonde Matrix

The norms of inverses of Vandermonde matrices were estimated by Gautschi [18, 19]. In some estimations there, the equality holds if all base points are on the same ray through the origin.

Compared to (3.31), for a small perturbation x, a bound of is investigated in the following lemma. Since the norm estimation of inverse of Vandermonde matrix must be interesting, we separate the result in this subsection from other ingredients for Theorem 3.1.

Lemma 3.5. If ∥x∥_∞ < 1/4π(2 + log cot(π/2N)), then

()

Proof. Let I = [δ_kn] be the identity matrix and W = V(0) ⁻¹V(x) − I, whose entries are

()

Since e^iθ − 1 = 2i sin(θ/2)e^iθ/2, the off-diagonal entries satisfy the following

()

The diagonal entries are estimated by the Cauchy mean value theorem as follows:

()

Regarding summations of |W_kn|, the maximum occurs when k = N/2 ± 1 from the symmetry of the sine function in (3.37). In both cases, we have

()

Since (3.39a), (3.39b), and (3.39c) imply ∥W ∥_∞ ≤ 1/2, we establish the following:

()

4. Numerical Results

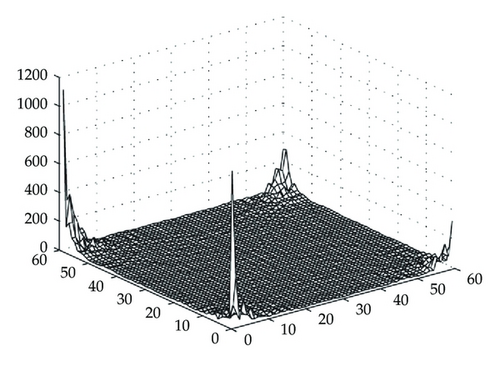
From the Biot-Savart law, we simulate the magnetic flux density B_z(n, m) induced by a horizontal current through the Logan shape ρ as in Figure 2, where N = 60. We obtain the simulated MR signals as depicted in Figure 3, through (3.1) with M = 32, δ = 0. We note that the maximum of B_z(n, m) is about 1/4 in Figure 2, larger than suggested in Theorem 3.1.

By discrete inverse Fourier transform for l, we transform

into

in (3.2). Then, setting for each fixed m,

()

the Newton iterations in (3.9) generate x^j with x⁰ = 0. The jth approximation

is done by

()

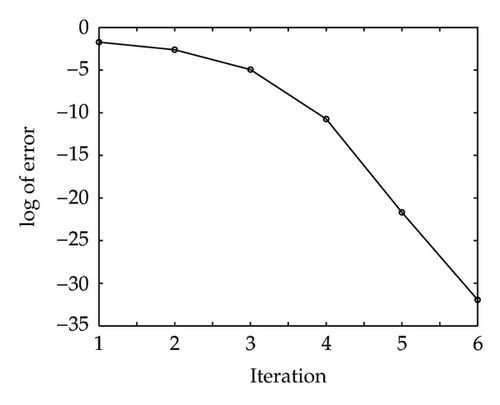
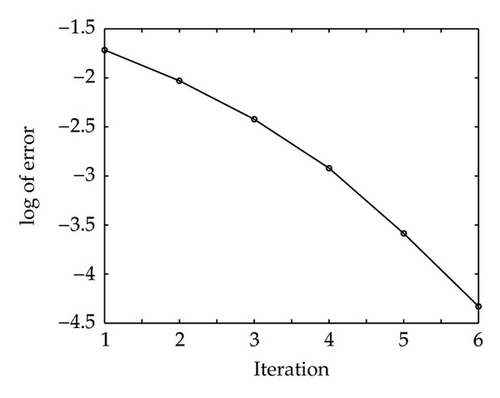
The log of error max _n,m | B_z(n, m) − B_z(n, m) ^j| is given in Figure 4(a), which means that the error decay is quadratic. In the Newton iterations in (3.9), we have to solve a Vandermonde system for V(x), which may be consuming time or unstable. Instead of V(x) in (3.7), we can fix V(0) and simplify the Newton iterations in (3.9). Then, the error decay is reduced to be linear as in Figure 4(b).

Acknowledgment

This paper was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2010-0022398, 2012R1A1A2009509).

References

1 Joy M., Scott G., and Henkelman M., In vivo detection of applied electric currents by magnetic resonance imaging, Magnetic Resonance Imaging. (1989) 7, no. 1, 89–94, 2-s2.0-0024561625.
10.1016/0730-725X(89)90328-7
CAS PubMed Web of Science® Google Scholar
2 Eyuboglu M., Birgul O., and Ider Y. Z., A dual modality system for high resolution.true conductivity imaging, Proceedings of the 11th International Conference on Electrical Bioimpedance (ICEBI ′01), 2001, 409–413.
Google Scholar
3 Ider Y. Z. and Birgul O., Use of the magnetic field generated by the internal distri- bution of injected currents for Electrical Impedance Tomography (MR-EIT), Elektrik. (1998) 6, 215–225.
Google Scholar
4 Khang H. S., Lee B. I., Oh S. H., Woo E. J., Lee S. Y., Cho M. H., Kwon O., Yoon J. R., and Seo J. K., J-substitution algorithm in magnetic resonance electrical impedance tomography (MREIT): phantom experiments for static resistivity images, IEEE Transactions on Medical Imaging. (2002) 21, no. 6, 695–702, 2-s2.0-0036591488, https://doi.org/10.1109/TMI.2002.800604.
10.1109/TMI.2002.800604
PubMed Web of Science® Google Scholar
5 Lee B. I., Oh S. H., Woo E. J., Lee S. Y., Cho M. H., Kwon O., Seo J. K., Lee J. Y., and Baek W. S., Three-dimensional forward solver and its performance analysis for magnetic resonance electrical impedance tomography (MREIT) using recessed electrodes, Physics in Medicine and Biology. (2003) 48, no. 13, 1971–1986, 2-s2.0-0038445928, https://doi.org/10.1088/0031%2D9155/48/13/309.
10.1088/0031-9155/48/13/309
PubMed Web of Science® Google Scholar
6 Oh S. H., Lee B. I., Woo E. J., Soo Y. L., Kim T. S., Kwon O., and Jin K. S., Electrical conductivity images of biological tissue phantoms in MREIT, Physiological Measurement. (2005) 26, no. 2, S279–S288, 2-s2.0-23044508481, https://doi.org/10.1088/0967%2D3334/26/2/026.
10.1088/0967-3334/26/2/026
PubMed Web of Science® Google Scholar
7 Sadleir R., Grant S., Zhang S. U., Oh S. H., Lee B. I., and Woo E. J., High field MREIT: setup and tissue phantom imaging at 11 T, Physiological Measurement. (2006) 27, no. 5, S261–S270, 2-s2.0-33745179196, https://doi.org/10.1088/0967%2D3334/27/5/S22.
10.1088/0967-3334/27/5/S22
PubMed Web of Science® Google Scholar
8 Scott G. C., Joy M. L. G., Armstrong R. L., and Henkelman R. M., Measurement of nonuniform current density by magnetic resonance, IEEE Transactions on Medical Imaging. (1991) 10, no. 3, 362–374, 2-s2.0-0026221249, https://doi.org/10.1109/42.97586.
10.1109/42.97586
CAS PubMed Web of Science® Google Scholar
9 Seo J. K., Yoon J. R., Woo E. J., and Kwon O., Reconstruction of conductivity and current density images using only one component of magnetic field measurements, IEEE Transactions on Biomedical Engineering. (2003) 50, no. 9, 1121–1124, 2-s2.0-0038644775, https://doi.org/10.1109/TBME.2003.816080.
10.1109/TBME.2003.816080
PubMed Web of Science® Google Scholar
10 Woo E. J., Seo J. K., and Lee S. Y., D. Holder, Magnetic resonance electrical impedance tomography (MREIT), Electrical Impedance Tomography: Methods, History and Applications, 2005, IOP Publishing, Bristol, UK.
Google Scholar
11 Joy M. L., MR current density and conductivity imaging: the state of the art, Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC ′04), 2004, San Francisco, Calif, USA, 5315–5319.
Google Scholar
12 Scott G. C., Joy M. L. G., Armstrong R. L., and Henkelman R. M., Sensitivity of magnetic-resonance current-density imaging, Journal of Magnetic Resonance. (1992) 97, no. 2, 235–254, 2-s2.0-0000178261.
10.1016/0022-2364(92)90310-4
CAS Web of Science® Google Scholar
13 Zhang N., Electrical impedance tomography based on current density imaging [M.S. thesis], 1992, Department of Electrical Engineering, University of Toronto, Toronto, Canada.
Google Scholar
14 Kwon O. I., Lee B. I., Nam H. S., and Park C., Noise analysis and MR pulse sequence optimization in MREIT using an injected current nonlinear encoding (ICNE) method, Physiological Measurement. (2007) 28, no. 11, 1391–1404, 2-s2.0-35848932318, https://doi.org/10.1088/0967%2D3334/28/11/006.
10.1088/0967-3334/28/11/006
PubMed Web of Science® Google Scholar
15 Park C., Lee B. I., Kwon O., and Woo E. J., Measurement of induced magnetic flux density using injection current nonlinear encoding (ICNE) in MREIT, Physiological Measurement. (2007) 28, no. 2, 117–127, 2-s2.0-33947723376, https://doi.org/10.1088/0967%2D3334/28/2/001.
10.1088/0967-3334/28/2/001
PubMed Web of Science® Google Scholar
16 Haacke E. M., Brown R. W., Thompson M. R., and Venkatesan R., Magnetic Resonance Imaging: Physical Principles and Sequence Design, 1999, John Wiley & Sons, New York, NY, USA.
Google Scholar
17 Kress R., Numerical Analysis, 1998, 181, Springer, New York, NY, USA, Graduate Texts in Mathematics, https://doi.org/10.1007/978%2D1%2D4612%2D0599%2D9, 1621952.
10.1007/978-1-4612-0599-9
Google Scholar
18 Gautschi W., On inverses of Vandermonde and confluent Vandermonde matrices, Numerische Mathematik. (1962) 4, 117–123, 0139627, https://doi.org/10.1007/BF01386302, ZBL0108.12501.
10.1007/BF01386302
Google Scholar
19 Gautschi W., Norm estimates for inverses of Vandermonde matrices, Numerische Mathematik. (1975) 23, 337–347, 0378382, ZBL0304.65031.
10.1007/BF01438260
Web of Science® Google Scholar

All articles

Newton Method to Recover the Phase Accumulated during MRI Data Acquisition

Abstract

1. Introduction