Comparison Study of Two Different Sun-Tracking Methods in Optical Efficiency of Heliostat Field

1. Introduction

Central receiver system (CRS) or central power tower is an attractive method to achieve tremendously huge power and high concentration of solar irradiance for electricity generation or thermal processes [1]. This system involves the use of many individual sun-tracking mirrors (or heliostats) to reflect and to superpose the concentrated sunlight at a common receiver attached on top of the central tower. The performance of the heliostat field is defined in terms of the optical efficiency which is the ratio of the net power absorbed by the receiver to the power incident normally on the field. The optical losses from the heliostat field take into account the losses due to the field layout, that is, cosine, shadowing and blocking, and losses due to other factors, that is, imperfect mirror reflectivity, atmospheric attenuation, and receiver spillage [2]. Although several number of heliostat field arrangement is possible, most of the heliostat field is designed in radial stagger pattern [3–6]. This arrangement ensures that no heliostat is consigned in front of another heliostat in adjacent rings along a spoke to the tower. Therefore, reflected beam from the heliostats can pass between adjacent neighbors direct to the receiver. Several studies have revealed that the radial stagger arrangement is the most efficient for a given land area as it cuts down the land usage and atmospheric attenuation losses. Hence, it contributes the most expedient distribution for heliostat fields [3, 7].

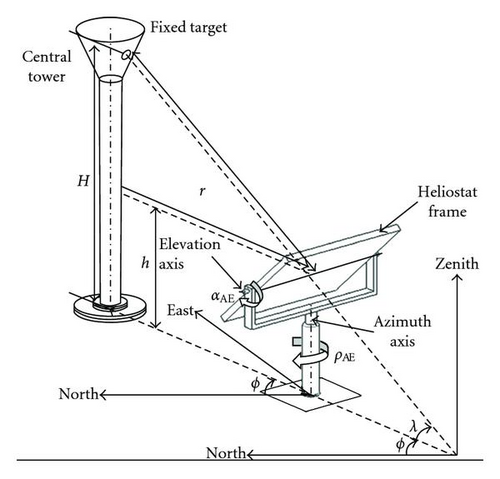
There are two major sun-tracking methods widely implemented in the heliostat, which are conventional method: Azimuth-Elevation (AE), and revolutionary method: Spinning-Elevation  (SE) [8–19]. In AE tracking method, one of the tracking axes of the heliostat points towards the zenith, namely, azimuth axis while the other axis is perpendicular to the first axis and tangent to the heliostat frame called elevation axis. In SE tracking method, one of the tracking axes of the heliostat points towards the target, namely, spinning axis in order to maintain the heliostat normal within the tangential plane, while the other axis is perpendicular to the first axis and tangent to the heliostat frame in order to adjust the heliostat normal within the tangential plane until it bisects the sun position vector and the target position vector called elevation axis. Since the positions of the sun and the receiver are independent of the sun-tracking method, the only difference between the AE and SE tracking system is the utilization of different mechanism to rotate the heliostat frame to achieve same incident angle but different orientation so that both can aim the sunlight towards the receiver.

In the previous comparison study for the heliostat field, the SE method consumes 4.8–9.3% lesser power on the sun-tracking system and can also reduce the geometrical radius of solar image by about 30% compared to that of AE method [8, 9, 20]. As a result, we would like to further explore the potential of both sun-tracking methods in the aspect of the optical efficiency in the field layout. In the new study, the losses due to the field layout such as cosine, shadowing, and blocking effects of both sun-tracking methods are analyzed and compared in details. Despite the existence of many algorithms for the AE tracking method, that is, DELSOL3, HFLCAL, WinDELSOL1.0, SENSOL, and so forth, in optimizing the heliostat field layout, there is no any algorithm yet to be developed for the SE tracking method [21–23]. In this paper, a more generalized algorithm is developed based on ray-tracing technique for the edge rays to determine blocking and shadowing areas for both tracking methods. The methodology and various measures of the new algorithm to analyze the optical efficiency of the heliostat field for both methods are described in details too.

2. Methodology

2.1. Sun-Tracking Formulas

For the completeness of the numerical analysis in the later section, the formulas of sun-tracking angles for both AE and SE methods applied in the new algorithm are listed as follows. From Figure 1(a), the elevation (α_SE) and spinning (ρ_SE) angles of heliostat using the SE method are expressed as follow:

$$ ()

In the case of cos ρ_SE > 0,

$$ ()

In the case of cos ρ_SE  < 0,

$$ ()

where

$$ ()

From Figure 1(b), the elevation (α_AE) and azimuth (ρ_AE) angles of AE method are expressed as follows:

$$ ()

In the case of cos ρ_AE > 0,

$$ ()

In the case of cos ρ_AE  < 0,

$$ ()

given that

$$ ()

and the incident angle is

$$ ()

The sun altitude (α) and azimuth (A) angles are defined as

$$ ()

If sin ω > 0, then A = 2π − A.

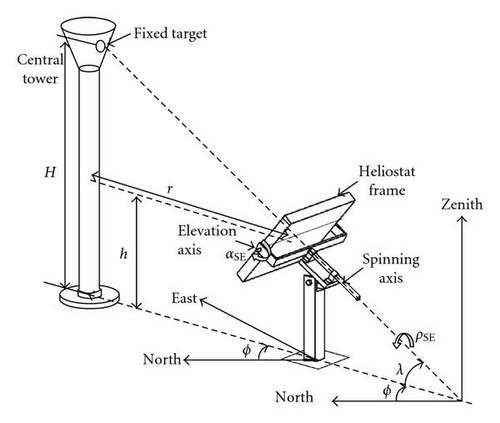
Where ϕ  is the facing angle, λ is the target angle,  Φ  is the latitude, ω is the hour angle, δ is the declination angle; ϕ = 0^° when the heliostat is due south of the target and it is positive value if the spinning axis is rotated from north to east direction; λ = 0^° if the heliostat is of the same height as the target and it is positive value when the spinning axis is rotated so that the target is higher than the heliostat.

2.2. Coordinate Transformations of Heliostat

Given that the sun is an apparent moving object while the target is a fixed object, the heliostat frame has to be adjusted to follow the apparent change of the sun position with time. In this case, to resolve the blocking and shadowing effects between the heliostats, the orientation of the heliostat frame must be first identified. The instantaneous orientation of the heliostat frame during the period of sun tracking in three dimensional space can be modeled by applying the coordinate transformation. For the convenience of the three-dimensional coordinate transformation, one more dimensionality of space is added as to make all the transformations linear.

Let the origin of global coordinate system, O(0,0, 0), as shown in Figure 2 be defined at the base of the central tower in such a way that the positive direction of X-axis pointing towards east, the positive direction of Y-axis pointing towards north, and the positive direction of Z-axis pointing towards zenith. The initial coordinate of the heliostat frame is defined in a local coordinate system as shown in Figure 3 wherein the origin of the coordinate system, C(0,0, 0), is located at the centre of the heliostat frame’s surface instead of the base of central tower. In this modeling, the heliostat frame is represented by four edge points assigned to the four corners of the moving frame. The coordinate of the edge points will be treated as a vector in the coordinate space, and it is written as

$$ ()

The final coordinate of the edge points for the heliostat frame after the coordinate transformation will be treated as a vector in matrix form written as

$$ ()

where k = 1 (for upper left corner of the heliostat frame), 2 (for upper right corner of the heliostat frame), 3 (for lower right corner of the heliostat frame), and 4 (for lower left corner of the heliostat frame).

In the coordinate transformation for the SE method, we consider two angular movements of the heliostat frame relative to the spinning and elevation axes as well as two initial orientation angles of the target-aligned heliostat named as the target angle and the facing angle. Finally, a translational coordinate transformation is required to transform the position of heliostat frame from the local coordinate system (attached to the local heliostat) to the global coordinate system (attached to the central power tower). The rotational transformation matrix for the elevation movement with angle α_SE can be written as

$$ ()

The rotational transformation matrix for the spinning movement with angle ρ_SE  can be written as

$$ ()

The rotational transformation matrix for the target angle λ can be written as

$$ ()

The rotational transformation matrix for the facing angle ϕ can be written as

$$ ()

The translational transformation matrix based on the coordinate of individual heliostat (H_cx, H_cy, H_cz) in the global coordinate system can be written as

$$ ()

where

$$ ()

H_cx is the distance of the heliostat in east-west direction (it is positive value if the heliostat is located on the east of the tower), H_cy is the distance of the heliostat in north-south direction (it is positive value if the heliostat is located on the north of the tower), H is the target height, and H_cz or h is the height of the heliostat.

After all the transformations, the final position of the SE heliostat frame can be known by using the following formula:

$$ ()

where the net coordinate transformation matrix for SE method is

$$ ()

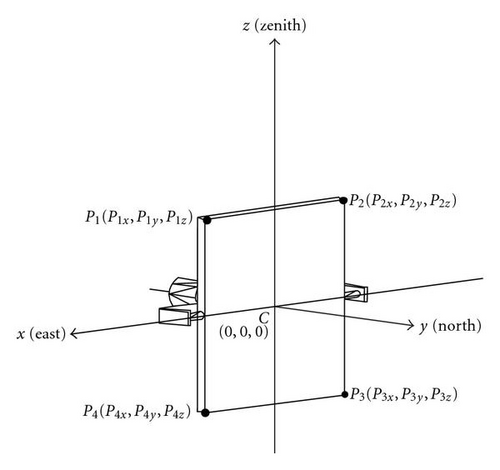
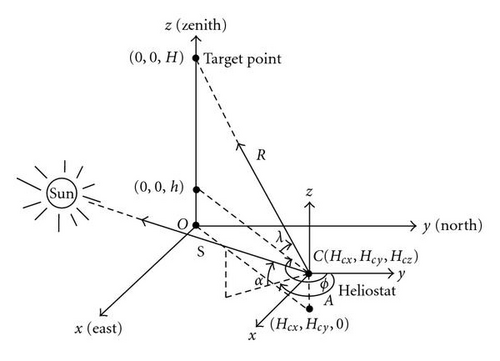
In the coordinate transformation for the AE sun-tracking method, we consider two angular movements of the heliostat frame relative to the azimuth and elevation axes and a translational transformation required to transform the position of heliostat frame from the local coordinate system to the global coordinate system.

The rotational transformation matrix for the elevation movement with angle α_AE can be written as

$$ ()

The rotational transformation matrix for the azimuth movement with angle ρ_AE can be written as

$$ ()

After all the rotational transformation, the final position of AE heliostat frame can found as

$$ ()

where the net coordinate transformation matrix for AE method is

$$ ()

From Figure 2, the unit vector for the incident sunray, S = (S_x, S_y, S_z), can be obtained as:

$$ ()

where α and A are the solar altitude and azimuth angles, respectively.

The reflected sunray by the heliostat, R = (R_x, R_y, R_z), can be described in terms of the target angle, and the facing angle of the heliostat as revealed in Figure 2. The components of the unit vector of the reflected sunray are as follows:

$$ ()

2.4. Optical Efficiency of Heliostat

For comparing the optical efficiency of two sun-tracking methods in the field layout, there are three major factors including cosine, shadowing, and blocking effects to be considered in our algorithm. In this context, the reflectivity of mirror is assumed to be perfect and the atmospheric attenuation is ignored in the study inasmuch as its strong dependency on the local weather condition as well as the aerosol distribution at ground level [10]. Both factors are also independent on the sun-tracking method that is the prime consideration in our study. Furthermore, the receiver spillage loss is not included in the algorithm of designing field layout as well because it involves different measure of study by taking into account the receiver design and the geometry of heliostat reflector.

Another major factor to influence the optical efficiency of the heliostat is the cosine efficiency, which is defined as the ratio of the projected heliostat area in the direction of beam insolation to the surface area. The cosine efficiency relies on both the sun’s position and the position of the heliostat relative to the receiver. The effective area of the heliostat’s reflector is reduced by the cosine of one-half of the angle between the incident sunray and a line from the heliostat to the receiver. Since the incident angle, θ, is independent on the tracking method, the cosine efficiency for both SE and AE heliostats is

$$ ()

Besides that, shadowing and blocking efficiencies also contribute to the optical performance of heliostat. Even though the shadowing and blocking efficiencies can be maximized by increasing the distance between heliostats, it has to sacrifice the packing factor of heliostat field in which more land area will be needed. In this case study, we maximize the effective use of land area in such a way that the distance between two adjacent heliostats is almost equal to the diagonal dimension of heliostat frame in order to study its effect to the blocking and shadowing efficiencies. The optical efficiency of heliostat caused by shadowing and blocking effects is computed using ray-tracing technique. For the convenience to resolve the reflective area of the “Test Heliostat” involved in the shadowing and blocking as illustrated in Figures 4(a) and 4(b), the directions of the incident sunray and reflected sunray are inverted to −S and -R, respectively. After computing the sun-tracking angles, the coordinate transformations for the “Adjacent Heliostat” (heliostat that causes shadowing or blocking to the incident sunray or the reflected sunray, resp.) and the “Test Heliostat” (heliostat which is tested for its shadowing and blocking efficiencies) are performed to simulate the tracking positions of both heliostats’ frames. Then, the “Ray/Plane Algorithm” is applied in the simulation to determine the shadowing area of the “Adjacent Heliostat” cast on the surface plane that represents the heliostat frame of “Test Heliostat” as illustrated in Figure 4(a). For the blocking effect, the reflected sunray from the “Test Heliostat” is used instead of incident sunray to calculate the blocking area projected on the surface plane of “Test Heliostat” as shown in Figure 4(b). The shadowing area, A_s, is also the reflective area of the “Test Heliostat” to be shadowed by the “Adjacent Heliostat.” The shadowing efficiency is calculated as follows

$$ ()

The blocking area, A_b, is also the reflective area of the “Test Heliostat,” wherein the reflected sunrays are blocked by the “Adjacent Heliostat.” The blocking efficiency is calculated as follows:

$$ ()

where A_t is the total reflective area of the “Test Heliostat.”

The algorithm to calculate the annual optical efficiency of individual heliostat and the overall heliostat field is summarized in the flow chart as shown in Figure 5. The operating period of the heliostat field ranges from solar time 0800 h (or t_s = 8) to 1600 h (or t_s = 16) and throughout the year with the calendar day from 1st January (or N = 1) to 31st December (or N = 365). For i-heliostat, the annual optical efficiency in the field layout can be calculated by using the formula:

$$ ()

where η_cos is the cosine efficiency, η_shadow is the shadow efficiency, and η_block is the blocking efficiency. On the other hand, the annual interception efficiency, the annual atmospheric transmission efficiency, and the mirror reflection efficiency are assumed to be unity [24]. The annual optical efficiency of heliostat field in the field layout can be calculated as

$$ ()

where i is the heliostat number.

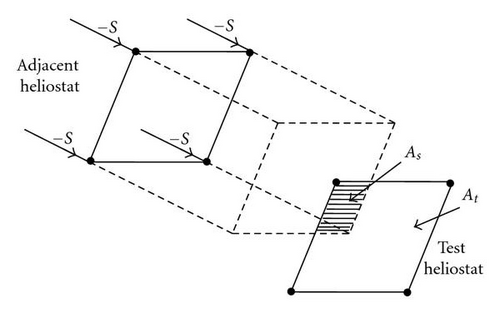
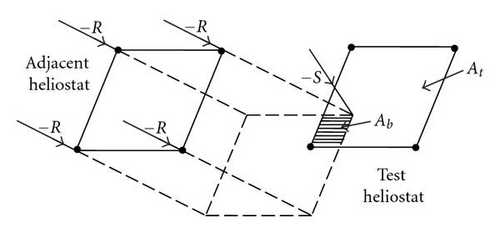
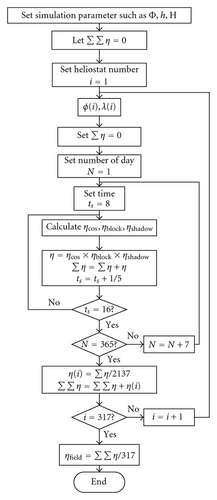
3. Result and Discussion

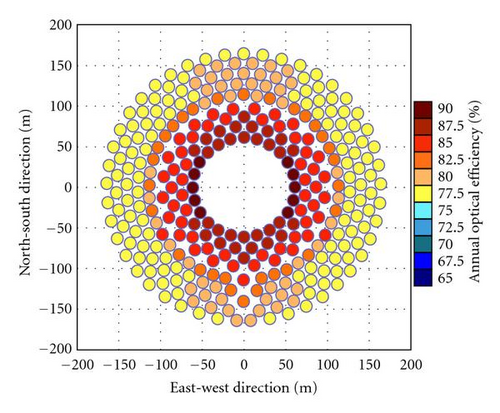
The simulation of the annual optical efficiency of heliostat field has been carried out to consider the cosine, shadowing, and blocking factors for both sun-tracking methods in different latitudes, that is, 0°, 15^°N, 30^°N. Figures 6(a) and 6(b) show the annual optical efficiency of individual heliostat in the field layout for a comparison of two methods at the latitude 0° (or at equator). The plots have shown that the annual optical efficiency for the heliostats in the east and west fields are perfectly symmetry as well as those in the south and the north fields. Furthermore, the annual optical efficiency of heliostats in north-south field is higher than those in east-west field. For the SE method, the annual optical efficiency of the individual heliostats is equal or higher than 77.5%. For AE method, the annual optical efficiency of the individual heliostat in this configuration is equal or higher than 75.0%. This figure has shown that SE method has an overall better optical efficiency than that of AE method at latitude 0°. For a comparison of two tracking methods, Figures 7(a), 7(b) and 8(a), 8(b) are also plotted to show the annual optical efficiency of heliostat field located at the latitude 15° N and 30° N, respectively. The simulated plots have shown that the annual optical efficiency of the east and west fields are perfectly symmetry regardless of sun-tracking methods. Nevertheless, it is asymmetry between north and south fields for both sun-tracking methods in which the north field has much higher annual optical efficiency than that of the south field. From our previous study for the range of motion, the characteristics of heliostat field located in the southern hemisphere can be implied from that of the northern hemisphere via rotating the heliostat field about the central tower by 180° because both of them are symmetry relative to the equator [9].

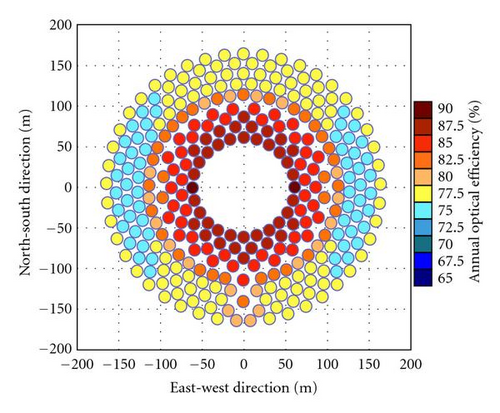
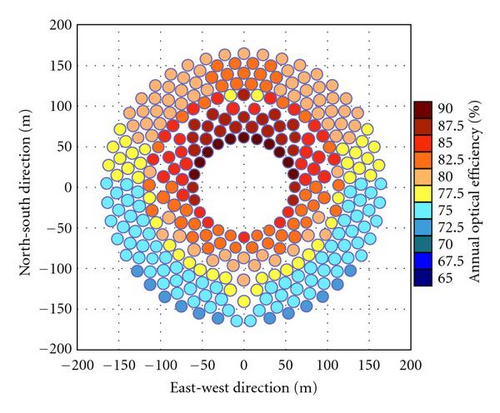
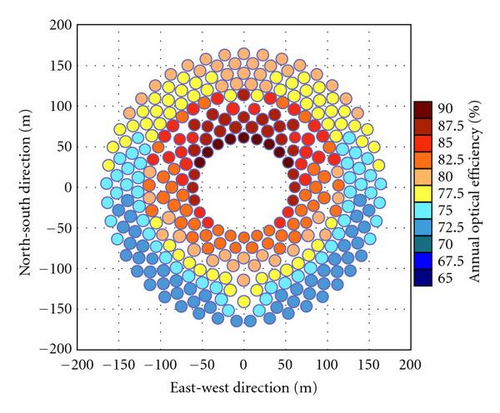
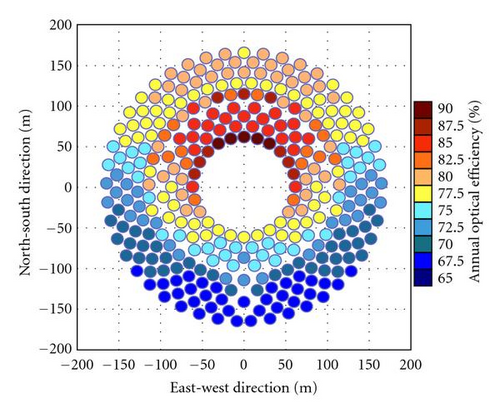
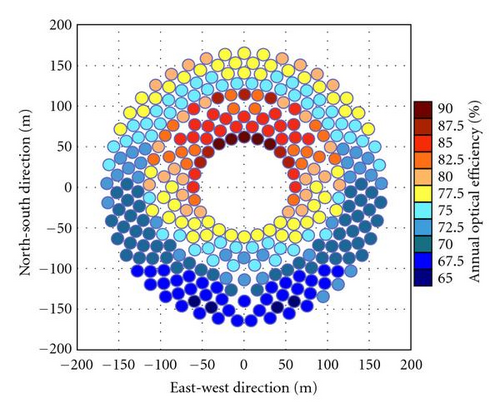
The simulated results for the annual optical efficiency of heliostat field for both sun-tracking methods at different latitudes, that is, 0°, 15° N, and 30° N, are summarized in Table 2. From the simulated result as revealed in Table  2, central tower system located at latitude at 0° has the highest annual optical efficiency of heliostat field compared to those of other latitudes. In addition, the latitude is inversely proportional to the annual field efficiency for both sun-tracking methods which means higher the latitude of the central power tower is located, the lower the optical efficiency of the heliostat field. All the efficiencies including cosine, blocking, and shadowing are the highest in equator and decrease with the latitude angle except the blocking efficiency for the AE method increases with the latitude angle.

The cosine efficiency for both sun-tracking methods is equal to each other at all latitudes. This is because the positions of the sun, heliostats, and target are exactly the same for both methods which leads to the same incident and reflected angles. Table 2 also shows that SE sun-tracking method has better shadowing and blocking efficiency compared to that of AE sun-tracking method at all latitude. Generally, the annual optical efficiency for SE method is higher than that of AE method in all latitudes.

4. Conclusions

Study on the optical efficiency of heliostat field for two sun-tracking methods has been conducted in details. Moreover, the algorithm to compute the annual field efficiency for both methods has also been developed. For a comparison of two sun-tracking methods, the cosine efficiency is equal for both methods whilst SE method has better shadowing and blocking efficiency compared to that of AE method. Thus, the overall annual field efficiency of SE method is about 0.8–1% greater than that of AE method. On the other hand, all the components of annual optical efficiency including cosine, blocking, and shadowing are the highest in equator and decrease with the latitude angle.