With the aid of symbolic computation, a new extended Jacobi elliptic function expansion method is presented by means of a new ansatz, in which periodic solutions of nonlinear evolution equations, which can be expressed as a finite Laurent series of some 12 Jacobi elliptic functions, are very effective to uniformly construct more new exact periodic solutions in terms of Jacobi elliptic function solutions of nonlinear partial differential equations. As an application of the method, we choose the generalized shallow water wave (GSWW) equation to illustrate the method. As a result, we can successfully obtain more new solutions. Of course, more shock wave solutions or solitary wave solutions can be gotten at their limit condition.

1. Introduction

In recent years, the nonlinear partial differential equations (NPDEs) are widely used to describe many important phenomena and dynamic processes in physics, mechanics, chemistry, biology, and so forth. With the development of soliton theory, There has been a great amount of activities aiming to find methods for exact solutions of nonlinear differential equations, such as Bäcklund transformation, Darboux transformation, Cole-Hopf transformation, similarity reduction method, variable separation approach, Exp-function method, homogeneous balance method, varied tanh methods, and varied Jacobi elliptic function methods [1–21].

Among those, the direct ansätz method [8–21] provides a straightforward and effective algorithm to obtain such particular solutions for a large number of nonlinear partial differential equations, in which the starting point is the ansätz that the solution sought is expressible as a finite series of special function, such as tanh function, sech function, tan function, sec function, sine-cosine function, Weierstrass elliptic function, theta function, and Jacobi elliptic function.

In this paper, a new Jacobi elliptic function expansion method is presented by means of a new general ansätz and is more powerful to uniformly construct more new exact doubly-periodic solutions in terms of Jacobi elliptic functions of nonlinear partial differential equations. The algorithm and its application are demonstrated later.

This paper is organized as follows. In Section 2, we summarize the extended Jacobi elliptic function expansion method. In Section 3, we apply the extended method to the generalized shallow water wave (GSWW) equation and bring out more new solutions. Conclusions will be presented in finally.

2. Summary of the Extended Jacobi Elliptic Function Expansion Method

In the following, we would like to outline the main steps of our extended method.

Step 1. For a given nonlinear partial differential equation with some physical fields u(x, y, t) in three variables x, y, t,

(2.1)

by using the wave transformation

(2.2)

where k, l, and c are constants to be determined later. Then the nonlinear partial differential equation (2.1) is reduced to a nonlinear ordinary differential equation (ODE):

(2.3)

Step 2. We introduce some new ansätz in terms of finite Jacobi elliptic function expansion in the following forms:

(1)
sn^′ξ/snξ expansion:
(2.4a)
(2)
cn^′ξ/cnξ expansion:
(2.4b)
(3)
dn^′ξ/dnξ expansion:
(2.4c)

where snξ, cnξ, dnξ are Jacobi elliptic sine function, the Jacobi elliptic cosine function, and the Jacobi elliptic function of the third kind, which are periodic and possess the following properties:

(1) properties of triangular functions

(2.5)

(2) derivatives of the Jacobi elliptic functions

(2.6)

where m is a modulus. The Jacobi-Glaisher functions for elliptic function can be found in [22, 23]. It is necessary to point out that above combinations only require solving the recurrent coefficient relation or derivative relation for the terms of polynomial for computation closed. Therefore, other Jacobi elliptic functions can be chosen to combine as new ansätz. For simplicity, we omit them here.

Step 3. In order to obtain the value of n in (2.4a)–(2.4c), we define the degree of u(ξ) as D[u(ξ)] = n, which gives rise to the degree of other expressions as

(2.7)

Therefore, we can get the value of n in (2.4a)–(2.4c). If n is a nonnegative integer, then we first make the transformation u = ωⁿ.

Step 4. Respectively substitute three cases of (2.4a)–(2.4c) into (2.3) along with (2.5) and (2.6) and then respectively set all coefficients of snⁱξcn^jξdn^kξ (i = 0,1, 2, …; j = 0,1; k = 0,1) to be zero to get an overdetermined system of nonlinear algebraic equations with respect to a₀, a_i, b_i, k, l, c (i = 0,1, 2, …).

Step 5. By use of the Maple software package “Charsets” by Dongming Wang, which is based on the Wu-elimination method [24], solving the overdetermined algebraic equations, we would end up with the explicit expressions for a₀, a_i, b_i, k, l, c (i = 0,1, 2, …). In this way, we can get periodic solutions with Jacobi elliptic function.

Since

(2.8)

u degenerate respectively as in the following form:

(1) solitary wave solutions:

(2.9a)

(2.9b)

(2) triangular function formal solutions:

(2.10a)

(2.10b)

So the new extended Jacobi elliptic function expansion method can obtain more new solutions, which contain solitary wave solutions, singular solitary solutions, and triangular function solutions. These new solutions cannot be obtained by other Jacobi elliptic function methods, such as Fu et al. [13], Fan [14], Yan [15–17], and Chen et al. [18–21].

3. Exact Solutions of the GSWW Equation

The Boussinesq approximation theory [25] for generalized classical shallow water wave leads to the GSWW equation:

(3.1)

where α and β are nonzero constants. Using v_x = u in [26], (3.1) can be simplified to

(3.2)

which has recently attracted many attentions from researchers under the following cases.

(1) For the case when α = 2β, the following AKNS-SWW equation:

(3.3)

was discussed by Ablowitz et al. [27].

(2) For the case when α = β, the following equation:

(3.4)

was discussed by Hirota and Satsuma [28].

The GSWW equation (3.1) in potential form was studied by Clarkson and Mansfield [26, 29] who gave a complete catalog of classical and nonclassical symmetry reductions. The necessary conditions of Painlevé tests were given by Weiss et al. [30] and the complete integrability of (3.1) for the case when α = 2β and α = β was established by Ablowitz et al. [31]. It has been proven by Hietarinta [32] that the GSWW equation (3.2) can be expressed in Hirota’s bilinear form and when α = 2β, (3.2) can be reduced to (3.3) or to (3.4) when α = β. In other words, both (3.3) and (3.4) are solvable by using Hirota’s bilinear method [33]. The N-soliton solutions for (3.3) and (3.4) had also been found using this technique [28]. Although there is no scaling transformation that can reduce (3.3) to (3.4), the classical methods of Lie, the nonclassical method of Bluman and Cole, and the direct method of Clarkson and Kruskal can be applied to solve the GSWW equation (3.2) to obtain some kinds of symmetry reductions [34, 35]. Recently, Elwakil found a lot of exact solutions by using the modified extended tanh-function method [36]. Yang and Hon employed a rational expansion to generalize Fan’s method for exact travelling wave solutions for the generalized shallow water wave (GSWW) equation [37].

According to the above method, to seek travelling wave solutions of (3.1), we make the following transformation:

(3.5)

where k and c are constants to be determined later. Thus (3.1) becomes

(3.6)

Equation (3.6) is integrated at once yielding

(3.7)

For the following, without loss of generality, we can set the integration constant equal to zero.

Now we consider the system (3.7) in the above three cases, so that (2.4a)–(2.4c). According to Step 2 and Step 3 in Section 2, by balancing the nonlinear term U² with the highest-order differential term U^′′ in (3.7), we suppose that (3.7) has the following formal solutions.

3.1. sn^′ξ/snξ Expansion

Now we consider the ansätz (2.4a). For (3.7), the ansätz (2.4a) becomes

(3.8)

where a₀, a₁, a₂, b₁, b₂, k, l and c are constants to be determined later.

With the aid of Maple, substituting (3.8) along with (2.5) and (2.6) into (3.7), yields a set of algebraic equations for snⁱξcn^jξdn^kξ (i = 0,1, 2, …; j = 0,1; k = 0,1). Setting the coefficients of these terms snⁱξcn^jξdn^kξ to be zero yields a set of overdetermined algebraic equations with respect to a₀, a₁, a₂, b₁, b₂, k, l, and c.

By use of the Maple software package “Charsets” by Dongming Wang, which is based on the Wu-elimination method [24], solving the overdetermined algebraic equations, we get the following results.

Case 1.

(3.9)

Case 2.

(3.10)

Case 3.

(3.11)

Case 4.

(3.12)

Case 5.

(3.13)

Case 6.

(3.14)

From (3.8) and Cases 1–6, we obtain the following solutions for (3.1).

Family 1. From (3.9), we obtain the following sn^′ξ/snξ expansion solutions for the GSWW equation as follows:

(3.15)

where

and c and k are arbitrary constants.

Family 2. From (3.10), we obtain the following sn^′ξ/snξ expansion solutions for the GSWW equation as follows:

(3.16)

where

and c and k are arbitrary constants.

Family 3. From (3.11), we obtain the following sn^′ξ/snξ expansion solutions for the GSWW equation as follows:

(3.17)

where

and c and k are arbitrary constants.

Family 4. From (3.12), we obtain the following sn^′ξ/snξ expansion solutions for the GSWW equation as follows:

(3.18)

where

and c and k are arbitrary constants.

Family 5. From (3.13), we obtain the following sn^′ξ/snξ expansion solutions for the GSWW equation as follows:

(3.19)

where

and c and k are arbitrary constants.

Family 6. From (3.14), we obtain the following sn^′ξ/snξ expansion solutions for the GSWW equation as follows:

(3.20)

where

and c and k are arbitrary constants.

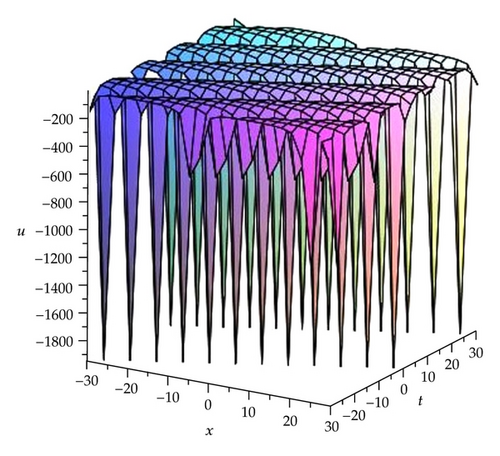
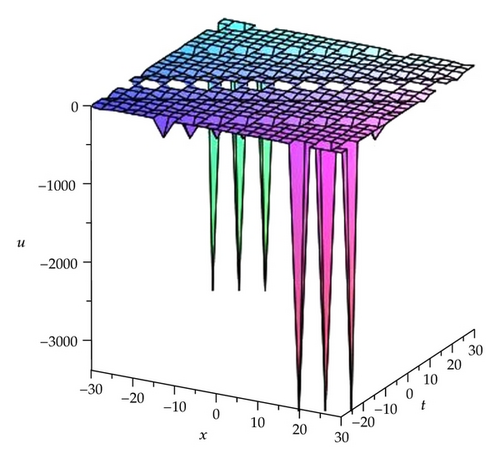
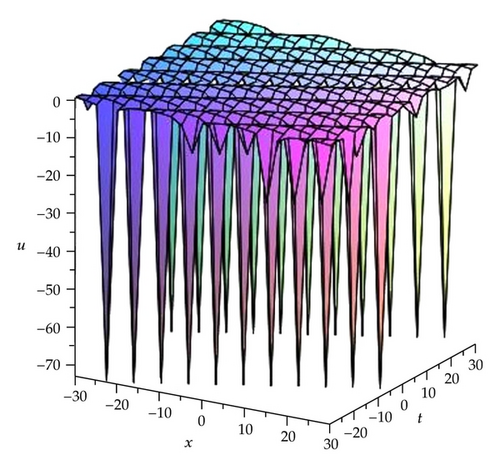
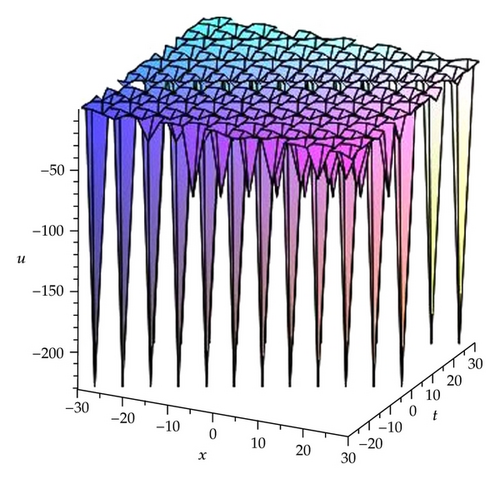
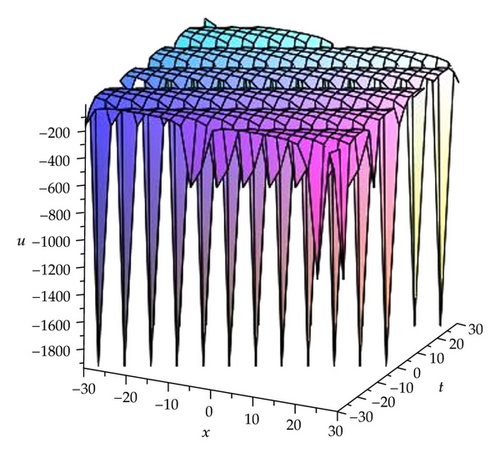
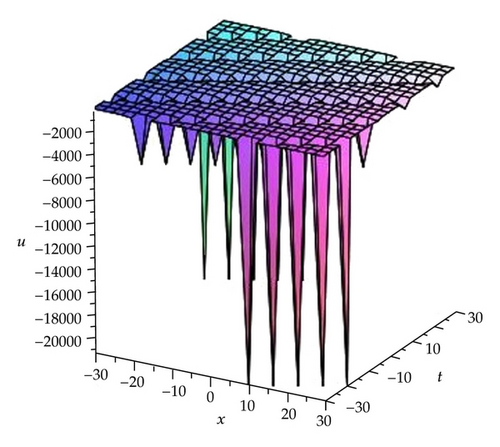
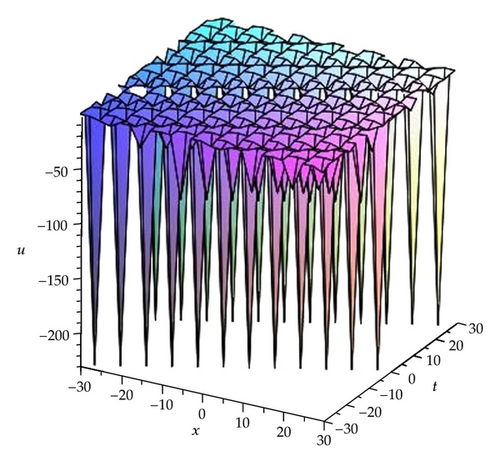
Remark 3.1. Here we find that the modulus m of the Jacobi elliptic functions has relations with c and k in Cases 1–6. To further analyze their relations, we take the solutions (3.9), (3.11), and (3.13) as samples by three figures (see Figures 1, 2, and 3).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Figure of m in (3.9).

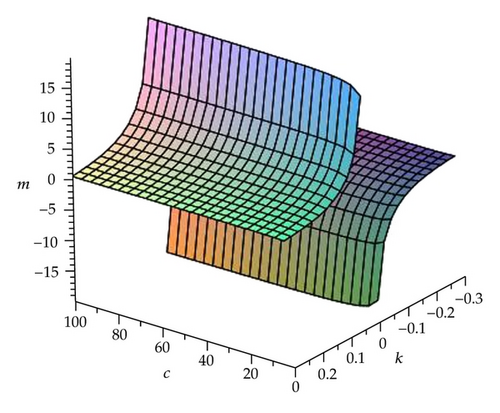
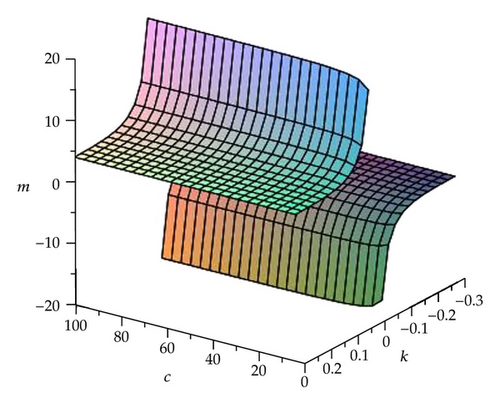
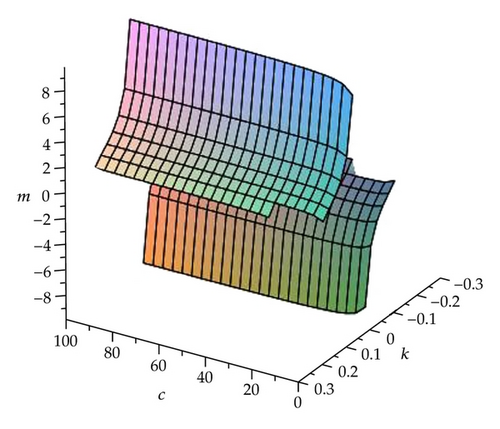
3.2. cn^′ξ/cnξ Expansion

Now we consider the ansätz (2.4b). For (3.7), the ansätz (2.4b) becomes

(3.21)

where a₀, a₁, a₂, b₁, b₂, k, l, and c are constants to be determined later. Following the same steps in Section 3.1, we can obtain the following cn^′ξ/cnξ expansion solutions.

Family 7.

(3.22)

where

and c and k are arbitrary constants.

Family 8.

(3.23)

where

and c and k are arbitrary constants.

Family 9.

(3.24)

where

and c and k are arbitrary constants.

Family 10.

(3.25)

where

and c and k are arbitrary constants.

Family 11.

(3.26)

where

and c and k are arbitrary constants.

Family 12.

(3.27)

where

and c and k are arbitrary constants.

3.3. dn^′ξ/dnξ Expansion

Now we consider the ansätz (2.4c). For (3.7), the ansätz (2.4c) becomes

(3.28)

where a₀, a₁, b₁, a₂, b₂, k, l, and c are constants to be determined later. Following the same steps in Section 3.1, we can obtain the following dn^′ξ/dnξ expansion solutions.

Family 13.

(3.29)

where

and c and k are arbitrary constants.

Family 14.

(3.30)

where

and c and k are arbitrary constants.

Family 15.

(3.31)

where

and c and k are arbitrary constants.

Family 16.

(3.32)

where

and c and k are arbitrary constants.

Family 17.

(3.33)

where

and c and k are arbitrary constants.

Family 18.

(3.34)

where

and c and k are arbitrary constants.

Remark 3.2. The solutions obtained here, to our knowledge, are all new families of periodic solution of the GSWW equation.

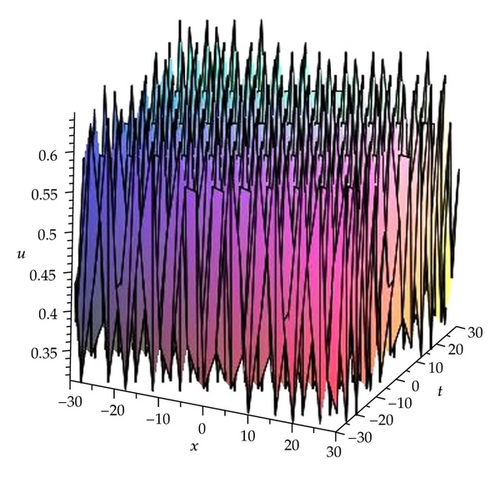
Remark 3.3. In order to understand the significance of these solutions in Families 1 and 18, here we take the solutions (3.15), (3.17), (3.19), (3.22), (3.24), (3.26), (3.29), (3.31), and (3.33) as samples to further analyze their properties by some figures (see Figures 4, 5, 6, 7,8, 9, 10, 11, and 12).

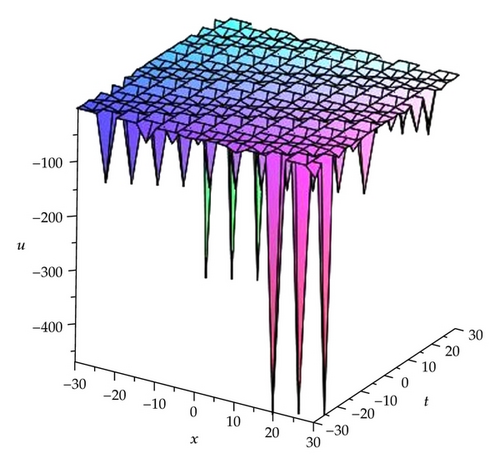
4. Conclusion and More General Form

In short, we have presented the new extended Jacobi elliptic function expansion method. The GSWW equation is chosen to illustrate the method such that many families of new Jacobi elliptic function solutions are obtained. When the modulus m → 1 or 0, some of these obtained solutions degenerate as solitary solutions or trigonometric function solutions. The algorithm can be applied to many nonlinear differential equations in mathematical physics. Other types of solutions of (2.1) need to be studied further.

It is easy to see that above-mentioned method is only applied to these nonlinear ODEs with constant coefficients or nonlinear partial differential equations, which can be reduced to the corresponding nonlinear ODEs with constant coefficients by using some transformations; otherwise, the method will not work. In order to overcome the disadvantage of the method, we change the method into a general form as follows.

If we do not reduce (2.1) to a nonlinear ODE (2.3) with constant coefficients, then we directly assume that (2.1) has the following solutions:

(1)
sn^′(ξ)/sn(ξ) expansion:
(4.1a)
(2)
cn^′(ξ)/cn(ξ) expansion:
(4.1b)
(3)
dn^′ξ/dnξ expansion:
(4.1c)

where a₀(x, t), a_i(x, t), b_i(x, t) (i = 1,2, …, n), and φ(x, t) are functions to be determined later. Substituting (4.1a), (4.1b), and (4.1c) with (2.5) and (2.6) into (2.1) yields a set of nonlinear partial differential equations with respect to these unknown functions a₀(x, t), a_i(x, t), b_i(x, t) (i = 1,2, …, n), and φ(x, t), respectively. If we can solve these functions from the obtained set of nonlinear partial differential equations, then we may obtain more types of doubly periodic solutions of (2.1). The more general form is better applied to nonlinear differential equations with variable coefficients. Particularly, if we only deduce the conclusions that all these function a₀(x, t), a_i(x, t), b_i(x, t) (i = 1,2, …) are all constants and φ(x, t) is of the form k(x − ct) (k, c constants), then the obtained results are the same as the ones found by using the method presented in Section 2. About the applications of the more general form, we will give some examples in future.

Conflict of Interests

The authors declare that they have no conflict of interests.

Acknowledgments

Many thanks are due to suggestions from the referees and support from the National Natural Science Foundation of China (Grant no. 61171179) and the Young Scientists Fund of the National Natural Science Foundation of China (Grant no. 10901145).

References

1 Ablowitz M. J. and Clarkson P. A., Solitons, Nonlinear Evolution Equations and Inverse Scattering, 1991, 149, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511623998, 1149378, ZBL0900.65350.
10.1017/CBO9780511623998
Google Scholar
2 Matveev V. B. and Salle M. A., Darboux Transformations and Solitons, 1991, Springer, Berlin, Germany, 1146435, ZBL1010.70503.
10.1007/978-3-662-00922-2
Google Scholar
3 Wadati M., Wave propagation in nonlinear lattice—I, Journal of the Physical Society of Japan. (1975) 38, 673–680, 0371296.
10.1143/JPSJ.38.673
Web of Science® Google Scholar
4 Clarkson P. A. and Kruskal M. D., New similarity reductions of the Boussinesq equation, Journal of Mathematical Physics. (1989) 30, no. 10, 2201–2213, https://doi.org/10.1063/1.528613, 1016286, ZBL0698.35137.
10.1063/1.528613
Web of Science® Google Scholar
5 Lou S.-Y. and Lu J., Special solutions from the variable separation approach: the Davey-Stewartson equation, Journal of Physics A. (1996) 29, no. 14, 4209–4215, https://doi.org/10.1088/0305%2D4470/29/14/038, 1406930, ZBL0899.35101.
10.1088/0305-4470/29/14/038
Google Scholar
6 He J.-H. and Abdou M. A., New periodic solutions for nonlinear evolution equations using Exp-function method, Chaos, Solitons & Fractals. (2007) 34, no. 5, 1421–1429, https://doi.org/10.1016/j.chaos.2006.05.072, 2335393, ZBL1152.35441.
10.1016/j.chaos.2006.05.072
Web of Science® Google Scholar
7 Wang M. L., Application of a homogeneous balance method to exact solutions of nonlinear equations inmathematical physics, Physics Letters A. (1996) 216, 67–75.
10.1016/0375-9601(96)00283-6
CAS Web of Science® Google Scholar
8 Wazwaz A.-M., The extended tanh method for new solitons solutions for many forms of the fifth-order KdV equations, Applied Mathematics and Computation. (2007) 184, no. 2, 1002–1014, https://doi.org/10.1016/j.amc.2006.07.002, 2294967, ZBL1115.65106.
10.1016/j.amc.2006.07.002
Web of Science® Google Scholar
9 Wazwaz A.-M., The tanh-coth method for solitons and kink solutions for nonlinear parabolic equations, Applied Mathematics and Computation. (2007) 188, no. 2, 1467–1475, https://doi.org/10.1016/j.amc.2006.11.013, 2335643, ZBL1119.65100.
10.1016/j.amc.2006.11.013
Web of Science® Google Scholar
10 Fan E., Extended tanh-function method and its applications to nonlinear equations, Physics Letters A. (2000) 277, no. 4-5, 212–218, https://doi.org/10.1016/S0375%2D9601(00)00725%2D8, 1827770, ZBL1167.35331.
10.1016/S0375-9601(00)00725-8
CAS Web of Science® Google Scholar
11 Parkes E. J. and Duffy B. R., An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equations, Computer Physics Communications. (1996) 98, 288–300.
10.1016/0010-4655(96)00104-X
CAS Web of Science® Google Scholar
12 Yan Z., New explicit travelling wave solutions for two new integrable coupled nonlinear evolution equations, Physics Letters A. (2001) 292, no. 1-2, 100–106, https://doi.org/10.1016/S0375%2D9601(01)00772%2D1, 1916507, ZBL1092.35524.
10.1016/S0375-9601(01)00772-1
CAS Web of Science® Google Scholar
13 Fu Z., Liu S., Liu S., and Zhao Q., New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations, Physics Letters A. (2001) 290, no. 1-2, 72–76, https://doi.org/10.1016/S0375%2D9601(01)00644%2D2, 1877700, ZBL0977.35094.
10.1016/S0375-9601(01)00644-2
CAS Web of Science® Google Scholar
14 Fan E., Uniformly constructing a series of explicit exact solutions to nonlinear equations in mathematical physics, Chaos, Solitons and Fractals. (2003) 16, no. 5, 819–839, https://doi.org/10.1016/S0960%2D0779(02)00472%2D1, 1964991, ZBL1030.35136.
10.1016/S0960-0779(02)00472-1
Web of Science® Google Scholar
15 Yan Z., Abundant families of Jacobi elliptic function solutions of the (2 + 1)-dimensional integrable Davey-Stewartson-type equation via a new method, Chaos, Solitons and Fractals. (2003) 18, no. 2, 299–309, https://doi.org/10.1016/S0960%2D0779(02)00653%2D7, 1983423.
10.1016/S0960-0779(02)00653-7
Web of Science® Google Scholar
16 Yan Z., The extended Jacobian elliptic function expansion method and its application in the generalized Hirota-Satsuma coupled KdV system, Chaos, Solitons and Fractals. (2003) 15, no. 3, 575–583, https://doi.org/10.1016/S0960%2D0779(02)00145%2D5, 1932475, ZBL1037.35074.
10.1016/S0960-0779(02)00145-5
Web of Science® Google Scholar
17 Yan Z., Extended Jacobian elliptic function algorithm with symbolic computation to construct new doubly-periodic solutions of nonlinear differential equations, Computer Physics Communications. (2002) 148, no. 1, 30–42, https://doi.org/10.1016/S0010%2D4655(02)00465%2D4, 1931201, ZBL1196.33017.
10.1016/S0010-4655(02)00465-4
CAS Web of Science® Google Scholar
18 Chen Y. and Wang Q., Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic function solutions to (1 + 1)-dimensional dispersive long wave equation, Chaos, Solitons and Fractals. (2005) 24, no. 3, 745–757, https://doi.org/10.1016/j.chaos.2004.09.014, 2116283.
10.1016/j.chaos.2004.09.014
Web of Science® Google Scholar
19 Chen Y., Wang Q., and Li B., Elliptic equation rational expansion method and new exact travelling solutions for Whitham-Broer-Kaup equations, Chaos, Solitons and Fractals. (2005) 26, no. 1, 231–246, https://doi.org/10.1016/j.chaos.2004.12.020, 2144553, ZBL1080.35080.
10.1016/j.chaos.2004.12.020
Web of Science® Google Scholar
20 Wang Q., Chen Y., and Zhang H., An extended Jacobi elliptic function rational expansion method and its application to (2 + 1)-dimensional dispersive long wave equation, Physics Letters A. (2005) 340, no. 5-6, 411–426, https://doi.org/10.1016/j.physleta.2005.04.034, 2137580.
10.1016/j.physleta.2005.04.034
CAS Web of Science® Google Scholar
21 Chen Y. and Wang Q., A new elliptic equation rational expansion method and its application to the shallow long wave approximate equations, Applied Mathematics and Computation. (2006) 173, no. 2, 1163–1182, https://doi.org/10.1016/j.amc.2005.04.061, 2208004, ZBL1088.65087.
10.1016/j.amc.2005.04.061
Web of Science® Google Scholar
22 Chandrasekharan K., Elliptic Function, 1978, Springer, Berlin, Germany.
Google Scholar
23 Du Val P., Elliptic Functions and Elliptic Curves, 1973, Cambridge University Press, London, UK, 0379512.
10.1017/CBO9781107359901
Google Scholar
24 Wu W. J., Algorithm and Computation, 1994, Springer, Berlin, Germany.
Google Scholar
25 Espinosa A. and Fujioka J., Hydrodynamic foundation and Painlevé analysis of Hirota-Satsuma-type equations, Journal of the Physical Society of Japan. (1994) 63, no. 4, 1289–1294, https://doi.org/10.1143/JPSJ.63.1289, 1280384, ZBL0972.35514.
10.1143/JPSJ.63.1289
Web of Science® Google Scholar
26 Clarkson P. A. and Mansfield E. L., On a shallow water wave equation, Nonlinearity. (1994) 7, no. 3, 975–1000, 1275537, https://doi.org/10.1088/0951%2D7715/7/3/012, ZBL0803.35111.
10.1088/0951-7715/7/3/012
Web of Science® Google Scholar
27 Ablowitz M. J., Kaup D. J., Newell A. C., and Segur H., The inverse scattering transform-Fourier analysis for nonlinear problems, 1974, 53, no. 4, 249–315, 0450815, ZBL0408.35068.
Google Scholar
28 Hirota R. and Satsuma J., N-soliton solutions of model equations for shallow water waves, Journal of the Physical Society of Japan. (1976) 40, no. 2, 611–612, 0397205.
10.1143/JPSJ.40.611
Web of Science® Google Scholar
29 Clarkson P. A. and Mansfield E. L., Symmetry reductions and exact solutions of shallow water wave equations, Acta Mathematicae Applicatae Sinica. (1995) 39, no. 1–3, 245–276, https://doi.org/10.1007/BF00994636, 1329564, ZBL0835.35006.
10.1007/BF00994636
Google Scholar
30 Weiss J., Tabor M., and Carnevale G., The Painlevé property for partial differential equations, Journal of Mathematical Physics. (1983) 24, no. 3, 522–526, https://doi.org/10.1063/1.525721, 692140, ZBL0531.35069.
10.1063/1.525721
Web of Science® Google Scholar
31 Ablowitz M. J., Ramani A., and Segur H., A connection between nonlinear evolution equations and ordinary differential equations of p-type—I, Journal of Mathematical Physics. (1980) 21, no. 4, 715–721, https://doi.org/10.1063/1.524491, 565716.
10.1063/1.524491
Web of Science® Google Scholar
32 Hietarinta J., R. Conte and N. Bocarra, Hirota′s bilinear method and partial integrability, Partially Integrable Evolution Equations in Physics, 1990, 310, Kluwer Academic Publishers, Dordrecht, The Netherlands, 459–478, NATO ASI Series C: Mathematical and Physical Sciences, 1073560, ZBL0717.58024.
10.1007/978-94-009-0591-7_17
Google Scholar
33 Hirota R., R. K. Bullough and P. J. Caudrey, Direct methods in soliton theory, Solitons, 1980, Springer, Berlin, Germany.
10.1007/978-3-642-81448-8_5
Web of Science® Google Scholar
34 Bluman G. W. and Cole J. D., The general similarity solution of the heat equation, Journal of Mathematics and Mechanics. (1969) 18, 1025–1042, 0293257.
Web of Science® Google Scholar
35 Clarkson P. A. and Kruskal M. D., New similarity reductions of the Boussinesq equation, Journal of Mathematical Physics. (1989) 30, no. 10, 2201–2213, https://doi.org/10.1063/1.528613, 1016286, ZBL0698.35137.
10.1063/1.528613
Web of Science® Google Scholar
36 Elwakil S. A., El-Labany S. K., Zahran M. A., and Sabry R., Modified extended tanh-function method and its applications to nonlinear equations, Applied Mathematics and Computation. (2005) 161, no. 2, 403–412, https://doi.org/10.1016/j.amc.2003.12.035, 2112413, ZBL1062.35082.
10.1016/j.amc.2003.12.035
Web of Science® Google Scholar
37 Yang Z. and Hon Y. C., A rational generalization of Fan′s method and its application to generalized shallow water wave equations, Applied Mathematics and Computation. (2010) 216, no. 7, 1984–1995, https://doi.org/10.1016/j.amc.2010.03.029, 2647067.
10.1016/j.amc.2010.03.029
Web of Science® Google Scholar

Citing Literature

All articles

A New Extended Jacobi Elliptic Function Expansion Method and Its Application to the Generalized Shallow Water Wave Equation

Abstract

1. Introduction

2. Summary of the Extended Jacobi Elliptic Function Expansion Method