Journal of Applied Mathematics
Volume 2012, Issue 1 875494
Research Article
Open Access

Accumulative Approach in Multistep Diagonal Gradient-Type Method for Large-Scale Unconstrained Optimization

Mahboubeh Farid, 

Corresponding Author

Mahboubeh Farid

Department of Mathematics, University Putra Malaysia, Selangor, 43400 Serdang, Malaysia upm.edu.my

Search for more papers by this author
Wah June Leong, 

Wah June Leong

Department of Mathematics, University Putra Malaysia, Selangor, 43400 Serdang, Malaysia upm.edu.my

Search for more papers by this author
Lihong Zheng, 

Lihong Zheng

School of Computing and Maths, Charles Sturt University, Mitchell, NSW 2795, Australia csu.edu.au

Search for more papers by this author
First published: 10 July 2012
https://doi.org/10.1155/2012/875494
Citations: 2
Academic Editor: Vu Phat

Abstract

This paper focuses on developing diagonal gradient-type methods that employ accumulative approach in multistep diagonal updating to determine a better Hessian approximation in each step. The interpolating curve is used to derive a generalization of the weak secant equation, which will carry the information of the local Hessian. The new parameterization of the interpolating curve in variable space is obtained by utilizing accumulative approach via a norm weighting defined by two positive definite weighting matrices. We also note that the storage needed for all computation of the proposed method is just O(n). Numerical results show that the proposed algorithm is efficient and superior by comparison with some other gradient-type methods.

1. Introduction

Consider the unconstrained optimization problem:
()
where f : Rn → R is twice continuously differentiable function. The gradient-type methods for solving (1.1) can be written as
()
where gk and Bk denote the gradient and the Hessian approximation of f at xk, respectively. By considering Bk = αkI, Barzilai and Borwein (BB) [1] give
()
where it is derived by minimizing ∥αk+1sk − yk∥2 respect to α with sk = xk+1 − xk and yk = gk+1 − gk. Recently, some improved one-step gradient-type methods [2–5] in the frame of BB algorithm were proposed to solve (1.1). It is proposed to let Bk be a diagonal nonsingular approximation to the Hessian and a new approximating matrix Bk+1 to the Hessian is developed based on weak secant equation of Dennis and Wolkowicz [6]
()
In one-step method, data from one previous step is used to revise the current approximation of Hessian. Later Farid and Leong [7, 8] proposed multistep diagonal gradient methods inspired by the multistep quasi-Newton method of Ford [9, 10]. In this multistep framework, a fixed-point approach for interpolating polynomials was derived from data in previous iterations (not only one previous step) [7–10]. General approach of multistep method is based on the measurement of distances in the variable space where the distance of every iterate is measured from one-selected iterate. In this paper, we are interested to develop multistep diagonal updating based on accumulative approach for defining new parameter value of interpolating curve. From this point, the distance is accumulated between consecutive iterates as they are traversed in the natural sequence. For measuring the distance, we need to parameterize the interpolating polynomial through a norm that is defined by a positive definite weighting matrix, say M. Therefore, the performance of the multistep method may be significantly improved by carefully defining the weighting matrix. The rest of paper is organized as follows. In Section 2, we discuss a new multistep diagonal updating scheme based on the accumulative approach. In Section 3, we establish the global convergence of our proposed method. Section 4 presents numerical result and comparisons with BB method and one-step diagonal gradient method are reported. Conclusions are given in Section 5.

2. Derivation of the New Diagonal Updating via Accumulative Approach

This section motivates to state new implicit updates for diagonal gradient-type method through accumulative approach to determining a better Hessian approximation at each iteration. In multistep diagonal updating methods, weak secant equation (1.4) may be generalized by means of interpolating polynomials, instead of employing data just from one previous iteration like in one-step methods. Our aim is to derive efficient strategies for choosing a suitable set of parameters to construct the interpolating curve and investigate the best norm for measurement of the distances required to parameterize the interpolating polynomials. In general, this method obeys the recursive formula of the form
()
where xk is the kth iteration point, αk is step length which is determined by a line search, Bk is an approximation to the Hessian in a diagonal form, and gk is the gradient of f at xk. Consider a differentiable curve x(τ) in Rn. The derivative of g(x(τ)), at point x(τ*), can be obtained by applying the chain rule:
()
We are interested to derive a relation that will be satisfied by the approximation of Hessian in diagonal form at xk+1. If we assume that x(τ) passes through xk+1 and choose τ* so that
()
then we have
()
As in this paper, we use two-step method, therefore; we use information of most recent points xk−1, xk, xk+1 and their associated gradients. Consider x(τ) as the interpolating vector polynomial of degree 2:
()
The selection of distinct scalar value τj efficiently through the new approach is the main contribution of this paper and will be discussed later in this section. Let h(τ) be the interpolation for approximating the gradient vector:
()
By denoting x(τ2) = xk+1 and defining
()
we can obtain our desired relation that will be satisfied by the Hessian approximation at xk+1 in diagonal form. Corresponding to this two-step approach, weak secant equation will be generalized as follows:
()
Then, Bk+1 can be obtained by using an appropriately modified version of diagonal updating formula in [3] as follows:
()
where . Now, we attempt to construct an algorithm for finding desired vector rk and wk to improve the Hessian approximation. The proposed method is outlined as follows. First, we seek to derive strategies for choosing a suitable set of values τ0, τ1, and τ2. The choice of is such that to reflect distances between iterates xk in Rn that are dependent on some metric of the following general form:
()
The establishment on τj can be made via the so-called accumulative approach where the accumulating distances (measured by the metric ϕM) between consecutive iterates are used to approximate τj. This leads to the following definitions (where without loss of generality, we take τ1 to be origin for value of τ):
()
Then, we can construct the set as follows:
()
where rk and wk are depending on the value of τ. As the set measures the distances, therefore they need to be parameterized the interpolating polynomials via a norm defined by a positive definite matrix M. It is necessary to choose M with some care, while improving the approximation of Hessian can be strongly influenced via the choice of M. Two choices for the weighting matrix M are considered in this paper. In first choice, if M = I, the ∥·∥M reduces to the Euclidean norm, and then we obtain the following τj values accordingly:
()
The second choice of weighting matrix M is to take M = Bk, where the current Bk is diagonal approximation to the Hessian. By these two means, the measurement of the relevant distances is determined by the properties of the current quadratic approximation (based on Bk) to the objective function:
()
Since Bk is a diagonal matrix, then it is not expensive to compute at each iteration. The quantity δ is introduced here and defined as follows:
()
and rk and wk are given by the following expressions:
()
()
To safeguard on the possibility of having very small or very large , we require that the condition
()
is satisfied (we use ɛ1 = 10−6 and ɛ2 = 106). If not, then we replace rk = sk and wk = yk. More that the Hessian approximation (Bk+1) might not preserve the positive definiteness in each step. One of the fundamental concepts in this paper is to determine an “improved” version of the Hessian approximation to be used even in computing the metric when M = Bk and a weighing matrix as norm should be positive definite. To ensure that the updates remain positive definite, a scaling strategy proposed in [7] is applied. Hence, the new updating formula that incorporates the scaling strategy is given by
()
where
()
This guarantees that the updated Hessian approximation is positive. Finally, the new accumulative MD algorithm is outlined as follows.

2.1. Accumulative MD Algorithm

Step 1. Choose an initial point x0 ∈ Rn, and a positive definite matrix B0 = I.

Let k : = 0.

Step 2. Compute gk. If ∥gk∥ ≤ ϵ, stop.

Step 3. If k = 0, set x1 = x0 − (g0/∥g0∥). If k = 1 set rk = sk and wk = yk go to Step 5.

Step 4. If k ≥ 2 and M = I is considered, compute from (2.13).

Else if M = Bk, compute from (2.14).

Compute δk, rk, wk and ηk, from (2.15), (2.16),  (2.17), and (2.20), respectively.

If , set rk = sk and wk = yk.

Step 5. Compute and calculate αk > 0 such that the Armijo [11], condition holds:

, where σ ∈ (0,1) is a given constant.

Step 6. Let , and update Bk+1 by (2.19).

Step 7. Set k : = k + 1, and return to Step 2.

3. Convergence Analysis

This section is devoted to study the convergence of accumulative MD algorithm, when applied to the minimization of a convex function. To begin, we give the following result, which is due to Byrd and Nocedal [12] for the step generated by the Armijo line search algorithm. Here and elsewhere, ∥·∥ denotes the Euclidean norm.

Theorem 3.1. Assume that f is a strictly convex function. Suppose the Armijo line search algorithm is employed in a way that for any dk with , the step length, αk satisfies

()
where αk ∈ [τ, τ′], 0 < τ < τ′ and σ ∈ (0,1). Then, there exist positive constants ρ1 and ρ2 such that either
()
or
()
is satisfied.

We can apply Theorem 3.1 to establish the convergence of some Armijo-type line search methods.

Theorem 3.2. Assume that f is a strictly convex function. Suppose that the Armijo line search algorithm in Theorem 3.1 is employed with dk chosen to obey the following conditions: there exist positive constants c1 and c2 such that

()
for all sufficiently large k. Then, the iterates xk generated by the line search algorithm have the property that
()

Proof. By (3.4), we have that either (3.2) or (3.6) becomes

()
for some positive constants. Since f is strictly convex, it is also bounded below. Then, (3.1) implies that f(xk + αkdk) − f(xk) → 0 as k → ∞. This also implies that ∥gk∥→0 as k → ∞ or at least
()

To prove that the accumulative MD algorithm is globally convergent when applied to the minimization of a convex function, it is sufficient to show that the sequence {∥Bk∥} generated by (2.19)-(2.20) is bounded both above and below, for all finite k so that its associated search direction satisfies condition (3.4). Since Bk is diagonal, it is enough to show that each element of Bk says ;  i = 1, …, n is bounded above and below by some positive constants. The following theorem gives the boundedness of {∥Bk∥}.

Theorem 3.3. Assume that f is strictly convex function where there exists positive constants m and M such that

()
for all x, z ∈ Rn. Let {∥Bk∥} be a sequence generated by the accumulative MD method. Then, ∥Bk∥ is bounded above and below for all finite k, by some positive constants.

Proof. Let be the ith element of Bk. Suppose B0 is chosen such that , where ω1 and ω2 are some positive constants.

Case 1. If (2.18) is satisfied, we have

()
By (2.18) and the definition of ηk, one can obtain
()
Thus, if , then B1 = η0B0 satisfies
()
On the other hand, if , then
()
where is the ith component of r0. Letting be the largest component (in magnitude) of r0, that is, ; for all i, then it follows that , and the property of , (3.12) becomes
()
Hence, is bounded above and below, for all i in both occasions.

Case 2. If (2.18) is violated, then the updating formula for B1 becomes

()
where is the ith component of s0, , and .

Because η0 ≤ 1 also implies that , then this fact, together with the convexity property (3.8), and the definition of η give

()
Using the similar argument as above, that is, by letting be the largest component (in magnitude) of s0, then it follows that
()

Hence, in both cases, is bounded above and below, by some positive constants. Since the upper and lower bound for is, respectively, independent to k, we can proceed by using induction to show that is bounded, for all finite k.

4. Numerical Results

In this section, we examine the practical performance of our proposed algorithm in comparison with the BB method and standard one-step diagonal gradient-type method (MD). The new algorithms are referred to as AMD1 and AMD2 when M = I and M = Bk are used, respectively. For all methods we employ Armijo line search [11] where σ = 0.9. All experiments in this paper are implemented on a PC with Core Duo CPU using Matlab 7.0. For each run, the termination condition is that ∥gk∥ ≤ 10−4. All attempts to solve the test problems were limited to a maximum of 1000 iterations. The test problems are chosen from Andrei [13] and Moré et al. [14] collections. The detailed test problem is summarized in Table 1. Our experiments are performed on a set of 36 nonlinear unconstrained problems, and the problems vary in size from n = 10 to 10000 variables. Figures 1, 2, and 3 present the Dolan and Moré [15] performance profile for all algorithms subject to the iteration, function call, and CPU time.

Table 1. Test problem and its dimension.
Problem Dimension References
Extended Trigonometric, Penalty 1, Penalty 2 10, …, 10000 Moré et al. [14]
Quadratic QF2, Diagonal 4, Diagonal 5, Generalized Tridiagonal 1
Generalized Rosenbrock, Generalized PSC1, Extended Himmelblau
Extended Three Exponential Terms, Extended Block Diagonal BD1
Extended PSC1, Raydan 2, Extended Tridiagonal 2, Extended Powell
Extended Freudenstein and Roth, Extended Rosenbrock 10, …, 10000 Andrei [13]
Extended Beale, Broyden Tridiagonal, Quadratic Diagonal Perturbed 10, …, 1000 Moré et al. [14]
Perturbed Quadratic, Quadratic QF1, Diagonal 1, Diagonal 2, Hager
Diagonal 3, Generalized Tridiagonal 2, Almost perturbed Quadratic
Tridiagonal perturbed quadratic, Full Hessian FH1, Full Hessian FH2
Raydan 1, EG2, Extended White and Holst 10, …, 1000 Andrei [13]
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Performance profile based on Iteration for all problems.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Performance profile based on function call.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Performance profile based on CPU time per iteration.

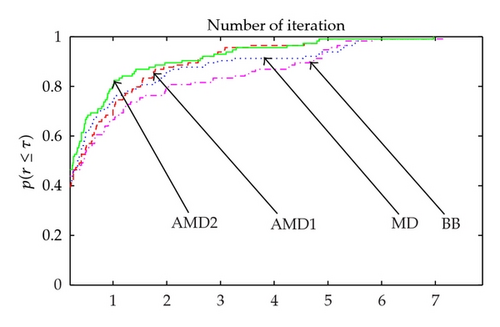
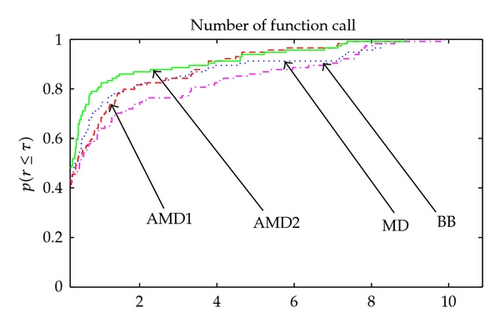
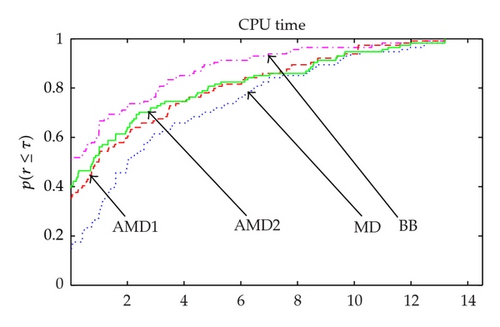
From Figure 1, we see that AMD2 method is the top performer, being more successful than other methods in the number of iteration. Figure 2 shows that AMD2 method requires the fewest function calls. From Figure 3, we observe that the AMD2 method is faster than MD and AMD1 methods and needs reasonable time to solve large-scale problems when compared to the BB method. At each iteration, the proposed method does not require more storage than classic diagonal updating methods. Moreover, a higher-order accuracy in approximating the Hessian matrix of the objective function makes AMD method need less iterations and less function evaluation. The numerical results by the tests reported in Figures 1, 2, and 3 demonstrate clearly the new method AMD2 shows significant improvements, when compared with BB, MD, and AMD1. Generally, M = Bk performs better than M = I. It is most probably due to the fact that Bk is a better Hessian approximation than the identity matrix I.

5. Conclusion

In this paper, we propose a new two-step diagonal gradient method as view of accumulative approach for unconstrained optimization. The new parameterization for multistep diagonal gradient-type method is developed via employing accumulative approach. The new technique is devised for interpolating curves which are the basis of multistep approach. Numerical results show that the proposed method is suitable to solve large-scale unconstrained optimization problems and more stable than other similar methods in practical computation. The improvement that our proposed methods bring does come at a complexity cost of O(n) while others are about O(n2) [9, 10].

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.