Modeling and Analysis of Peer-to-Peer Botnets

1. Introduction

A botnet is a network of thousands (or more) of compromised hosts under the control of a botnetmaster, which usually recruits new vulnerable computers by running all kinds of malicious software (malware), such as Trojan horses, worms, computer viruses, and so forth [1]. For a variety of nefarious purposes, a botnetmaster who operates a botnet controls remotely those zombie computers to pursuit various malicious activities, such as distributed denial-of-service attacks (DDoS), email spam, password cracking, and so forth [2]. Botnets have been turned out one of the most serious threat to Internet [3].

To effectively fight against botnets, researchers have endeavored to explore working mechanisms of botnets from different perspectives in the past few years (see [4–11]). These existing researches provide perfect insight into detection and elimination of botnets. Aiming at describing the dynamical characteristics of botnets, Dagon et al. [12] constructed a Susceptible-Infective-Recovered (SIR) model, which took into account the effect of time and location on malware spread dynamics. The model accurately characterizes the population growth of a botnet. Considering the interactions among botnets, Song et al. [1] presented the interaction game model among botnets to investigate the effect of the cooperation and the competition on the number of botnet individuals.

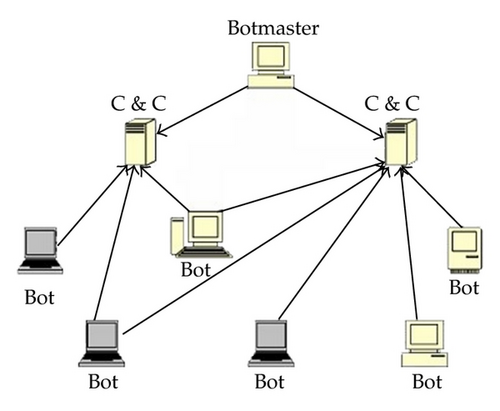
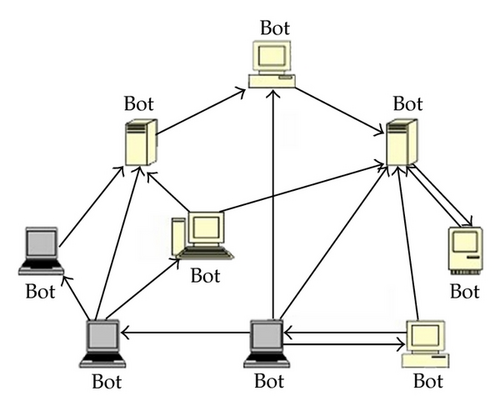
Most previous botnets as shown in Figure 1 use Internet relay chat (IRC) as a form of communication for centralized command and control (C&C) structure. Botnets based on C&C structure are easily checked and cracked by defenders; as well as the threats of botnets can be mitigated and eliminated if the central of C&C is unavailable [13]. In comparison, Peer-to-Peer (P2P) betnets as shown in Figure 2 employing a distributed command-and-control structure are more robust and more difficult for the security community to defend. Thus, P2P botnets, such as Trojan.Peacomm, Storm botnet [14], have emerged and gradually escalated in recent years. The threats of P2P botnets to Internet security have drawn widespread attention. Reference [15] presented a stochastic model of Storm Worm P2P botnet to examine how different factors, such as the removal rate and the initial infection rate, impact the total propagation bots. Kolesnichenko et al. developed a mean-field model to analyze P2P botnet behaviors [16]. In their seminal work, Yan et al. [17] mathematically elaborated the performance of a new type of P2P botnet—AntBot from perspectives of reachability, resilience to pollution and scalability. They also developed a P2P botnet simulator to evaluate the effectiveness of analysis. Furthermore, the authors suggested some potential defense schemes for defenders to effectively disrupt AntBot operations.

For security workers to be better prepared for potentially destructive P2P botnets, it is necessary for them to understand deeply factors that influence the formation of P2P botnets. Against this backdrop, in this paper, we utilize mathematical modeling method to investigate how immunizations affect the dynamical actions of P2P botnets. Our key contributions are summarized as follows: (i) we propose novel dynamical models which reflect the formation of P2P botnets; (ii) we derive mathematically the feasible region of immunization and depict their numerical simulations; (iii) we suggest a probable immune method for researchers and security professionals.

The remainder of the paper is organized as follows. Section 2 elaborates modeling mechanism. In Section 3, we derive the equilibria of models and prove their stabilities. In Section 4, we get the mathematical expressions of immune feasible regions and obtain the results of numerical simulations. In Section 5, we depict the numerical simulations to verify conclusions of Section 4. Section 6 concludes this paper with some conclusions.

2. Modeling P2P Botnets

Considering bot candidates and the network a botnet attaches itself to, we roughly divide P2P botnets into three categories [18]: (i) Parasite P2P botnet, in which all bot members are chosen from an existing P2P network; (ii) Leaching P2P botnet, which is a botnet that bot candidates are from vulnerable hosts throughout the Internet, but they will join in and depend on an existing P2P network; (iii) Bot-only P2P botnet, which refers to a botnet that occurs in an unattached network, and there are no nonmalignant peers except bots.

For parasite P2P botnet, once a vulnerable host is compromised by botnet malware, it will directly become a bot member and serve for the botmaster without further joining the botnet. Up to this trait, in Section 2.1, we present a deterministic mathematical model named “microlevel model” to reflect its dynamical features. However, many botmasters extend their scales to the whole Internet to recruit new zombies because the scale of parasite botnet is limited by the number of peers in an existing P2P network. For constructing this type P2P botnet, there are two steps: the first step is trying to infect new vulnerable hosts throughout the whole Internet, and the second step is new compromised hosts joining into network and connecting with other bots. In Section 2.2, we use a novel mathematical model, which we call “macrolevel model” to characterize their dynamical actions.

3. Model Analysis

To achieve the effective region of f and g, we first obtain the stable equilibria for systems (2.4) and (2.7).

4. Control Strategies of P2P Botnets

Theorems 3.2 and 3.6 indicate that P2P botnets will be eliminated if reasonable antivirus strategies are taken (represented by the formulations of $$ and R₀). Here, we will investigate effective methods eliminating P2P botnets by deriving the feasible region of f and g.

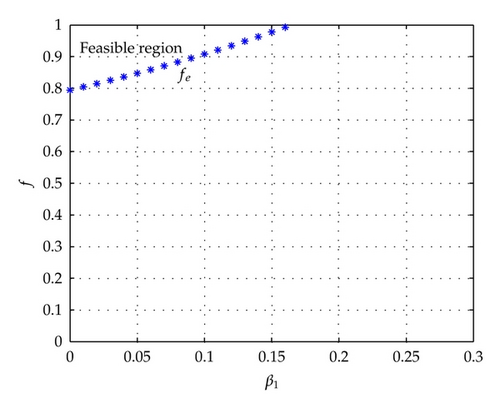
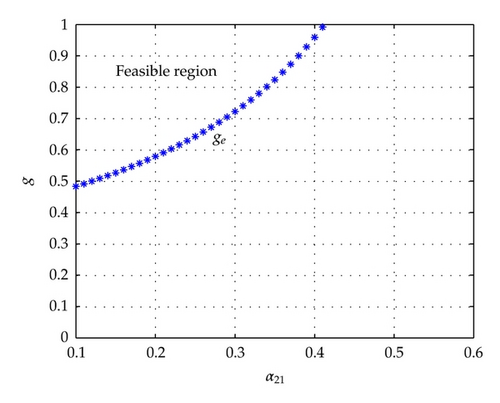
The numerical solution of f_e obtained from (4.2) is plotted with different value of β₁ and fixed values of $$, and $$ in Figure 3. Similarly, Figure 4 depicts the numerical solution of g_e obtained from (4.5) with different value of α₂₁ and fixed values of μ = 2.28  ×  10⁻⁴,  δ = 0.5,  r_s = 0.015,  r₁ = 0.0059, r₂ = 0.0059, α₁₂ = 0.5, α₁₁ = 0.1, and α₂₂ = 0.7.

5. Numerical Simulations

To validate the accuracy of f_e obtained from (4.2), we simulate system (2.4) with the following parameters:  N = 100000,   μ = 2.28E − 4,   β₂ = 0.8,  r_s = 0.0059,   r_i = 0.0059,   β₁ = 0.1, and (i) f = 0.95, where f > f_e = 0.9079; (ii) f = 0.6, where f < f_e = 0.9079. Initial values are set to S(0) = 99998, I(0) = 10, and R(0) = 0, respectively. Figures 5 and 6 show the simulation results with the above two sets of parameters, respectively, which are consistent with theoretical prediction.

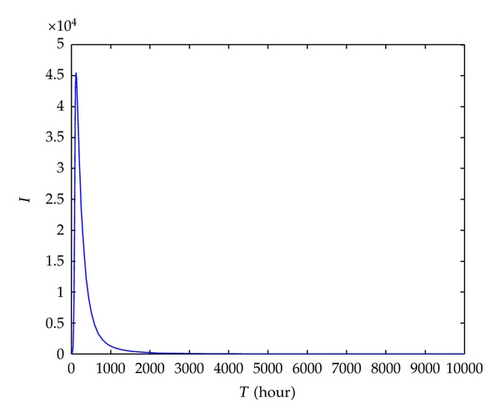
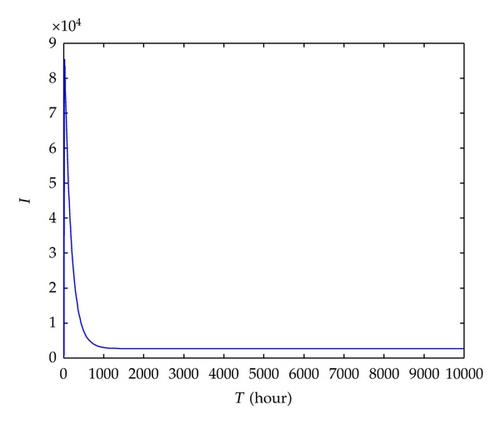
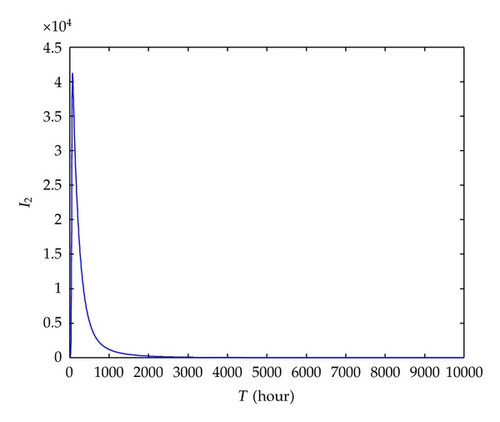
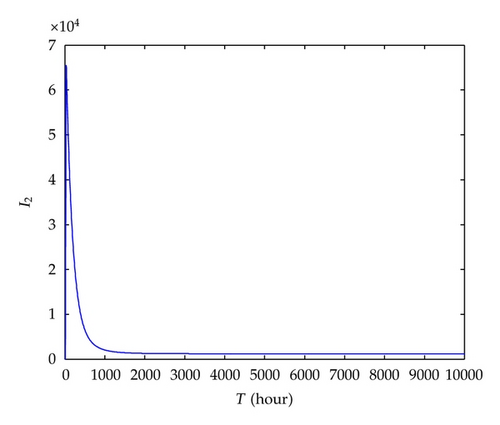
Similarly, we verify the accuracy of g_e obtained from (4.5) by simulating system (2.7). The following parameter values are adopted:  μ = 2.28E − 4,  α₁₁ = 0.1,  α₁₂ = 0.5,  α₂₁ = 0.3,  α₂₂ = 0.7,   δ = 0.5,  r_s = 0.015,  r₁ = r₂ = 0.0059, and (i) g = 0.9, where g > g_e = 0.7221; (ii) g = 0.2, where g < g_e = 0.7221. Initial values are set to S(0) = 99996, I₁ (0) = 2, I₂(0) = 2, and R(0) = 0, respectively. Simulation results in Figures 7 and 8 are consistent with theoretical prediction.

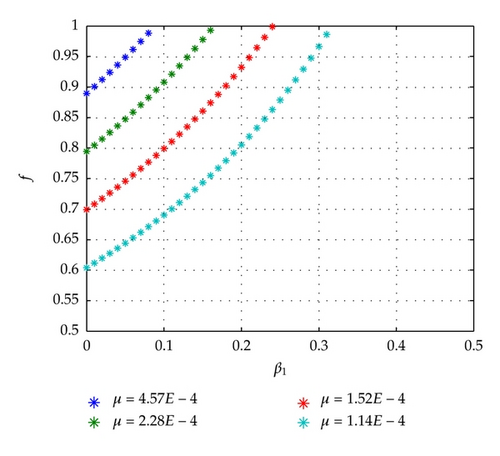
For investigating the effect of different replacement rate $$ on f, we depict simulation results of f_e in Figure 9, in which we set $$, and 4.57E − 4, that is, replacement time is one year, nine months, a half year, and three months. Other parameters are the same to Figure 3.

Similarly, for investigating the effect of μ on g, we set μ = 1.14E − 4,   2.28  ×  10⁻⁴, 3.42E − 4, and 4.57E − 4; other parameters are the same to Figure 4. The simulation result is depicted in Figure 10.

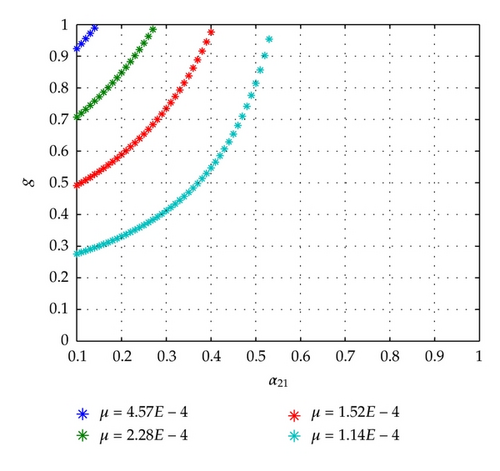
Figures 9 and 10 reflect the fact that decreasing the replacement rate of computers can enhance the effectiveness of immunizations. This finding contributes to management and maintenance of networks at a cost-effective way.

6. Conclusions

As a kind of new form of botnets, P2P botnets have attracted considerable attention. In this paper, the authors explore two novel dynamical models. The first is a micro-level model which describes the dynamical behavior of Parasite P2P botnets. The Second is the macro-level model which characterizes the dynamical action of Leaching P2P botnet. Throughout the paper, we focus on the effect of immunization on dynamics of P2P botnets. Through detailed mathematical analysis, the feasible region of immunization has been derived. In addition, we simulate the feasible region of immunization by using different parameter values. Furthermore, the correctness of feasible region has been verified.

The thresholds of immunizations have demonstrated that antivirus strategies have great influence on the dynamics of P2P botnets. More specifically, in feasible regions of immunizations, the spread of computer viruses will be stopped, and the botnet will be cracked. In contrary, immune measures merely decrease the scale of hosts infected by computer viruses, and the botnet will survive. In addition, our results also show that the replacement rate of computers will affect the threshold of immunizations.

Our investigations can provide insight on the effectiveness of various antivirus measures (e.g., antivirus products and user education). According to the thresholds of (4.2) and (4.5), secure organizations can make cost-effective countermeasures to work well in practice. Our study is only limited to unstructured P2P networks, such as Gnutella. Taken a step further, our models are adapted to topology-independent malware, such as file-sharing worms, viruses, Trojans, and so on. In the future, we will concentrate our attentions on the propagation model of topology-aware malware.