Phase-Conjugate-State Pairs in Entangled States
Abstract
We consider the probability that a bipartite quantum state contains phase-conjugate-state (PCS) pairs and/or identical-state pairs as signatures of quantum entanglement. While the fraction of the PCS pairs directly indicates the property of a maximally entangled state, the fraction of the identical-state pairs negatively determines antisymmetric entangled states such as singlet states. We also consider the physical limits of these probabilities. This imposes fundamental restrictions on the pair appearance of the states with respect to the local access of the physical system. For continuous-variable system, we investigate similar relations by employing the pairs of phase-conjugate coherent states. We also address the role of the PCS pairs for quantum teleportation in both discrete-variable and continuous-variable systems.
1. Introduction
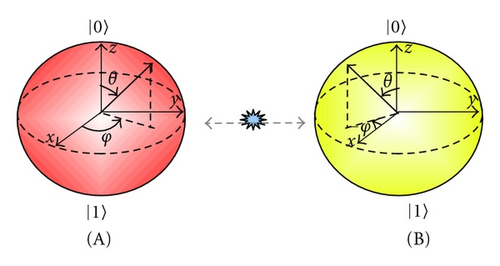
It has been known that the use of PCS pairs {|ψ〉|ψ*〉} is more efficient than the use of identical-state pairs, {|ψ〉|ψ〉}, in the transmission of unknown quantum states. Gisin and Popescu showed that the set of antiparallel spins stores the quantum information better than the set of parallel spins [6]. Zhou et al. provided a generalization of this relation by exploiting unknown PCS and identical-state pairs for two-qudit systems [7]. Similar relations have been found in the continuous variable system in which a set of phase-conjugate coherent-state pairs, say {|α〉|α*〉}, is employed [8]. Other insightful properties of the pairs of coherent states have been investigated from the aspect of the optimal cloning [9]. A scheme of continuous variable cloning of phase-conjugate coherent states is proposed in [10] and an experimental demonstration has been reported in [11].
In this paper we define the probabilities that PCS and/or identical-state pairs appear in bipartite quantum states. We investigate physical limits of these probabilities and their relations to quantum entanglement. In Section 2, we define the fraction of the PCS and/or identical-state pairs on a two-qudit system and investigate their properties. For the case of the uniform distribution, the fractions determine the symmetry of bipartite quantum states in the sense of [12]. It is shown that the fraction of the PCS pairs corresponds to the average fidelity of quantum teleportation. We consider similar relations with respect to two mutually unbiased bases in Section 2.5. We also consider the phase-conjugate pairs of coherent states for a two-mode continuous-variable system in Section 3. The results are summarized in Section 4.
2. Two-Qudit System
2.1. Phase-Conjugate-State Pairs in Two-Qudit States
Let us write a maximally entangled state (MES) in two-qudit (two d-level) system composed of subsystems A and B as . This state has an interesting property associated with a local projection (see Figure 1): if a subsystem A is projected onto a pure state ψ then the state of the other subsystem B becomes the phase conjugate of the pure state . In equation, we have the relation for any pure state ψ. Here, the factor comes from the probability that the subsystem A is in ψ, that is, Tr (A〈ψ| | Φ0,0〉〈Φ0,0| | ψ〉 A) = 1/d. Note that the phase conjugation is defined with respect to a fixed basis. Any maximally entangled state has the same property up to local unitary operation.
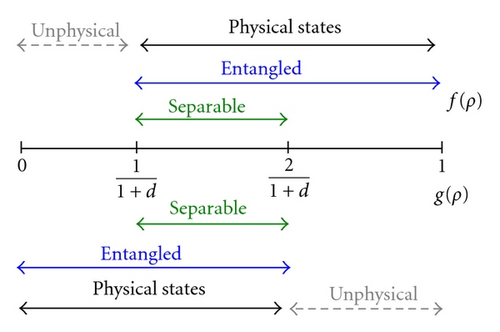
From (5), it is also clear that the MES maximizes the probability of the pair appearance and f = 1 uniquely determines . We thus have positive answers to the question (ii) and obtain the separable condition from the classical limit on the fraction of the PCS pairs associated with the question (i).
2.2. Phase-Conjugate-State Pairs and Average Fidelity of Quantum Teleportation
In this section we consider the process of quantum teleportation and show that the teleportation fidelity corresponds to the fraction of the PCS pairs introduced in the previous section (see (2)).
Equation (20) shows that the teleportation fidelity is determined by the fraction of the PCS pairs. Hence, we can understand that the role of the entangled state in quantum teleportation is to generate the phase-conjugate state in a (remote) local system when the state of the other local system is projected onto a pure state. Note that the classical boundary of the fidelity achieved by the entanglement breaking channel [13] corresponds to the classical limit fraction of the PCS pairs defined in (4).
2.3. Identical-State Pairs in Two-Qudit States
In this section we consider the probability that a two-qudit state contains identical-state pairs {|ψ〉|ψ〉}. We show its physical limits and relation to entanglement.
Note that the unconditional appearance (the appearance with unit probability) of the orthogonal pairs is the unique property of the states in the antisymmetric subspace. This can be proven as follows: the condition g = 0 implies Tr ρ(|ψ〉〈ψ | ) ⊗2 = 0 for any state |ψ〉 since |ψ〉〈ψ | ≥ 0. Suppose that ψ is a “qubit” state so that |ψ〉 ⊗2 = (α | i〉+β | j〉)(α | i〉+β | j〉) with |α|2+|β|2 = 1. Then, the condition Tr ρ(|ψ〉〈ψ | ) ⊗2 = 0 for any α and β yields that ρ is the singlet state . Since this relation must hold for any choice of i and j, the states have to be in the antisymmetric subspace spanned by the singlets .
2.4. Summary of the Statements for the Uniform Average over the d-Level Local States
- (i)
for any bipartite state .
- (ii)
is entangled if .
- (iii)
iff .
- (iv)
corresponds to the teleportation fidelity.
- (i)
for any bipartite state .
- (ii)
is entangled if .
- (iii)
is in antisymmetric subspace iff .
2.5. Two Mutually Unbiased Bases
In the previous sections the pair appearances are considered with respect to the uniform distribution that includes arbitrary PCS/identical-state pairs. In this section we consider the appearance of the PCS pairs with respect to the elements of two mutually unbiased bases.
The two orthonormal bases of a d-level system, say {|j〉} and , are said to be mutually unbiased if they satisfy the relation for any k and j [17]. Here we use a fixed Z basis {|j〉} and its Fourier basis defined by with . We refer to as the X basis since they are eigenstates of defined in (11). By definition, the elements of the Z basis are unchanged under the phase conjugation |j*〉 = |j〉 whereas the elements of the X basis changes under the phase conjugation as .
Let us consider some cases of prime numbers. For d = 2 we have and min ρ∈Sep. fm(ρ) = (1/2)(1 − 1/d) = 1/4. The equality is achieved by |0,1〉. Therefore we obtain another inseparable inequality for the regime of smaller fm: is entangled if . Note that, in the case of d = 2, we have and , and there is no difference between the fraction of PCS pairs and the fraction of identical state pairs. This gives a different structure from f and g in the diagram of Figure 2.
3. Two-Mode Continuous-Variable System
In the following sections we will consider continuous-variable analog of the pair appearance of phase-conjugate states. The analysis in Sections 3.1 and 3.2 is continuous-variable counterpart of the analysis on the two-qudit system described in Sections 2.1 and 2.2.
3.1. Conjugate-State Pairs on Continuous-Variable Systems
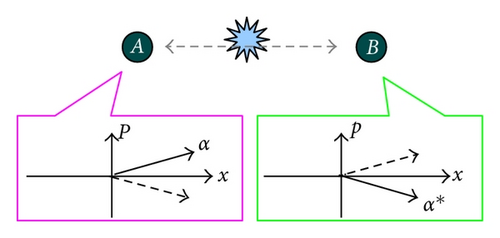
The EPR state is defined as a simultaneous eigenstate of the relative position and total momentum of a two-particle system. The EPR state thus has strong correlation on the positions and strong anticorrelation on the momentums. This suggests that the complex amplitudes of the two particles maintain the complex conjugate relation as in Figure 4. To be concrete, let us consider the form of the EPR state |EPR〉 = ∫ | x〉|x〉dx = ∫ | p〉| − p〉dp [1]. Here, |x〉 and are the eigenkets of the canonical operators and belong to the eigenvalues x and p, respectively. Here and in what follows we assume the commutation relations for canonical operators . We can verify and . We can also rewrite this state in the coherent state basis by using the over completeness relation π−1∫ | α〉〈α | d2α = 1 as |EPR〉 = π−1∫ | α〉|α*〉d2α. This expression demonstrates the pair appearance of the complex conjugate coherent states, {|α〉|α*〉}.
In what follows we show that (i) the maximum value of f in (43) for physical states is actually given by fmax of (48) and determine (ii) the maximum value of f for classically correlated states.
Let us show that (i) λfmax (λ, ζ) corresponds to the operator norm of , that is, . To proceed, we determine the covariance matrix of and diagonalize this matrix.
Proof. Let us define the covariance matrix of
In order to diagonalize this matrix we define another matrix U(r) corresponding to the two-mode squeezing operator that transforms the canonical operators as follows:
Note that in the limit λ → 0, we have fmax → 1 for any ζ > 0. This means that with nearly unit probability, the TMSS assigns the complex-conjugate pair of coherent states as the EPR state does (see Figure 4). Note also that the maximum eigenvalue can be associated with the physical limit of the amplification task in [20].
Proof. In order to show this, let us write the partial transposition of the operator in the diagonal form:
Consequently, it has turned out that the pair appearance of the phase-conjugate coherent states can be a signature of entanglement, and we obtain the following statement: the state ρ is entangled if there exist λ > 0 and ζ > 0 such that [21] (see Figure 5).
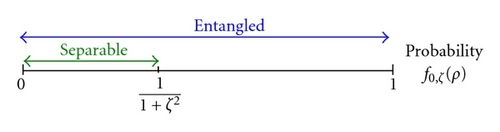
In Section 2.3, it is shown that the fraction of the identical-state pairs vanishes for the antisymmetric states and a smaller value of g can be a signature of entanglement on the two-qudit system. For the fraction of the identical-coherent-state pairs {|α〉|ζα〉} with the prior distribution pλ(α), it is clear that one can lower the expectation value less than any given positive number by choosing a product of number states with a sufficiently large photon number. Hence, the fraction of the identical-coherent-state pairs is not useful as a signature of entanglement in this regard.
3.2. Teleportation Fidelity and the Pair Appearance of Phase-Conjugate Coherent States
In this section we consider the process of continuous-variable quantum teleportation and investigate the equivalence between the teleportation fidelity and the fraction of the phase-conjugate coherent-state pairs.
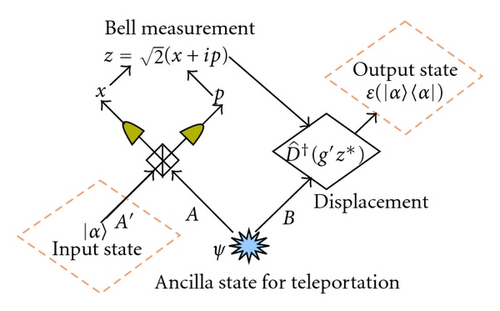
4. Summary
We have considered the probability that a bipartite quantum state contains the PCS pairs and/or identical-state pairs. We determine the physical limits and classical limits of these probability for the case of uniform distribution on qudit states. The classical limits give the separable conditions. We have also shown the equivalence between the average fidelity of quantum teleportation process and the probability of the PCS pairs on the resource state of the teleportation. A summary of the obtained statements in Sections 2.1–2.3 is given in Section 2.4.
For the case of uniform distribution on two mutually unbiased bases, a part of the problems becomes highly dependent on the dimension d. We have shown that the probability of the identical-state-pair appearance is useless for the entanglement verification when d is not a prime number. We have conjectured that the probability can be a signature of entanglement when d is a prime number. It is true when d = 2 and is numerically confirmed when d = 3.
We have also considered the probability that a two-mode continuous-variable state contains the phase-conjugate coherent-state pairs. We determine its physical limit and classical limit. We have also addressed its role in the process of continuous-variable quantum teleportation.
Acknowledgments
This work was supported by the Grant-in-Aid for the Global COE Program “The Next Generation of Physics, Spun from Universality and Emergence” from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. R. Namiki acknowledges support from JSPS.
Appendices
A. Maximum Separable Eigenvalue of Pure Entangled States
In the main text, we have considered the maximum expectation value of certain observables under the constraint that the state is separable. This optimization problem is called the separable eigenvalue problem [26]. If the observable is an entangled pure state, the maximum value is the square of the largest Schmidt coefficient. Here we provide a formal proof.
Proof. Any pure entangled state can be written in the Schmidt decomposed form as follows:
B. Another Expression of the Flip Operator
Here, we give another diagonal expression of the flip operator defined in (24). In the main text we use the diagonal expression of (26).




