There are various methods regarding project selection in different fields. This paper deals with an actual application of construction project selection, using two aggregation operators. First, the opinion of experts is used in a model of group decision making called intuitionistic fuzzy TOPSIS (IFT). Secondly, project evaluation is formulated by dynamic intuitionistic fuzzy weighted averaging (DIFWA). Intuitionistic fuzzy weighted averaging (IFWA) operator is utilized to aggregate individual opinions of decision makers (DMs) for rating the importance of criteria and alternatives. A numerical example for project selection is given to clarify the main developed result in this paper.

1. Introduction

Project selection and project evaluation involve decisions that are critical in terms of the profitability, growth, and survival of project management organizations in the increasingly competitive global scenario. Such decisions are often complex, because they require identification, consideration, and analysis of many tangible and intangible factors [1].

There are various methods regarding project selection in different fields. Project selection problem has attracted great endeavor by practitioners and academicians in recent years. One of the major fields that have been applied to this problem is mathematical programming, especially Mix-Integer Programming (MIP), since the problems comprise selection of projects while other aspects are considered using real-value variables [2]. For instance, a MIP model is developed by [3] to conquer Research and Development (R&D) portfolio selection.

Multicriteria decision making (MCDM) is a modeling and methodological tool for dealing with complex engineering problems [4]. Many mathematical programming models have been developed to address project-selection problems. However, in recent years, MCDM methods have gained considerable acceptance for judging different proposals. The objective of Mohanty’s [5] study was to integrate the multidimensional issues in an MCDM framework that may help decision makers to develop insights and make decisions. They computed weight of each criterion and then assessed the projects by doing technique for order preference by similarity to ideal solution algorithm (TOPSIS) [6]. To select R&D project, the application of the fuzzy analytical network process (ANP) and fuzzy cost analysis has been used by some researchers [7]. In their studies, triangular fuzzy numbers (TFNs) are used to prefer one criterion over another by using a pairwise comparison with the fuzzy set theory, where the weight of each criterion in the format of triangular fuzzy numbers is calculated [7]. The project selection problem was presented through a methodology which is based on the analytic hierarchy process (AHP) for quantitative and qualitative aspects of a problem [8]. It assists the measuring of the initial viability of industrial projects. The study shows that industrial investment company should concentrate its efforts in development of prefeasibility studies for a specific number of industrial projects which have a high likelihood of realization [8].

Multiattribute decision making (MADM) is the other applied approach in which criteria are mostly defined in qualitative scale and the decision is made with respect to assigned weights using some methods, such as PROMETHEE [9, 10]. To have more comprehensive study on MADM methods in this field, readers are referred to [11–15].

The rest of the paper is organized as follows. Section 2 provides materials and methods, mainly fuzzy set theory (FST) and intuitionistic fuzzy set (IFS). The IFT and DIFWA are introduced in Section 3. How the proposed model is used in an actual example is explained in Section 4. Finally, the conclusions are provided in the final section.

2. Materials and Methods

2.1. FST

Zadeh (1965) introduced the fuzzy set theory (FST) to deal with the uncertainty due to imprecision and vagueness. A major contribution of this theory is capability of representing vague data; it also allows mathematical operators and programming to be applied to the fuzzy domain. An FS is a class of objects with a continuum of grades of membership. Such a set is characterized by a membership function, which assigns to each object a grade of membership ranging between zero and one [16, 17].

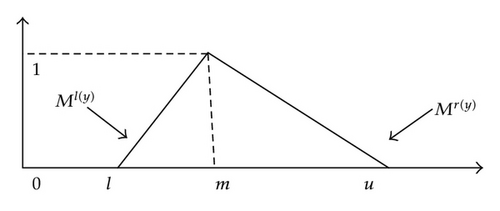
A tilde “~” will be placed above a symbol if the symbol represents an FST. A TFN is shown in Figure 1. A TFN is denoted simply as (l/m, m/u) or (l, m, u). The parameters l, m and u (l ≤ m ≤ u), respectively, denote the smallest possible value, the most promising value, and the largest possible value that describe a fuzzy event. The membership function of TFN is as follows.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A TFN .

Each TFN has linear representations on its left and right side, such that its membership function can be defined as

()

A fuzzy number can always be given by its corresponding left and right representation of each degree of membership as in the following:

()

where l(y) and r(y) denote the left side representation and the right side representation of a fuzzy number (FN), respectively. Many ranking methods for FNs have been developed in the literature. These methods may provide different ranking results, and most of them are tedious in graphic manipulation requiring complex mathematical calculation [18].

While there are various operations on TFNs, only the important operations used in this study are illustrated. If we define two positive TFNs (l1, m1, u1) and (l2, m2, u2), then

()

2.2. Basic Concept of IFS

The application of IFS method within the overall goal to select the best project has been described. IFSs introduced by Atanassov [19] are an extension of the classical FST, which is a suitable way to deal with vagueness. IFSs have been applied to many areas such as medical diagnosis [20–22], decision-making problems [23–46], pattern recognition [47–52], supplier selection [53, 54], enterprise partners selection [55], personnel selection [56], evaluation of renewable energy [57], facility location selection [58], web service selection [59], printed circuit board assembly [60], and management information system [61].

The following briefly introduces some necessary introductory concepts of IFS. IFS A in a finite set X can be written as [19]

()

are membership function and nonmembership function, respectively, such that

()

A third parameter of IFS is π_A(x), known as the intuitionistic fuzzy index or hesitation degree of whether x belongs to A or not:

()

It is obviously seen that for every x ∈ X

()

If it is small, knowledge about x is more certain. If π_A(x) is great, knowledge about x is more uncertain. Obviously, when

()

for all elements of the universe, the ordinary FST concept is recovered [60].

Let A and B be IFSs of the set X, then multiplication operator is defined as follows [19]:

()

3. Intuitionistic Fuzzy TOPSIS (IFT) and Dynamic Intuitionistic Fuzzy Weighted Averaging (DIFWA) Methods

3.1. IFT

It should be mentioned here that the presented approach mainly utilizes the IFT method presented in [53, 56, 57] to handle a project selection problem with six projects and six criteria. In the current paper we validate the method in an actual context and show this method applicability with an extensive set of selection criteria. The IFT method is a suitable way to deal with MCDM problem in intuitionistic fuzzy environment (IFE). Let A = {A₁, A₂, …, A_m} be a set of alternatives and let X = {X₁, X₂, …, X_n} be a set of criteria, the procedure for IFT method has been conducted in eight steps presented as follows.

Step 1. Determine the weights of importance of DMs.

In the first step, we assume that decision group contains l = {l₁, l₂, …, l_n} DMs. The importances of the DMs are considered as linguistic terms. These linguistic terms were assigned to IFN. Let D_k = [μ_k, v_k, π_k] be an intuitionistic fuzzy number for rating of kth DM.Then the weight of kth DM can be calculated as

()

Step 2. Determine intuitionistic fuzzy decision matrix (IFDM).

Based on the weight of DMs, the aggregated intuitionistic fuzzy decision matrix (AIFDM) was calculated by applying intuitionistic fuzzy weighted averaging (IFWA) operator Xu [62]. In group decision-making process, all the individual decision opinions need to be fused into a group opinion to construct AIFDM.

Let be an IFDM of each DM. λ = {λ₁, λ₂, λ₃, …, λ_l} is the weight of DM. Consider

()

where

()

Step 3. Determine the weights of the selection criteria.

In this step, all criteria may not be assumed to be of equal importance. W represents a set of grades of importance. In order to obtain W, all the individual DM opinions for the importance of each criteria need to be fused. Let be an IFN assigned to criterion X_j by the kth DM.

The weights of the criteria can be calculated as follows:

()

Thus, a vector of criteria weight is obtained: W = [w₁, w₂, w₃, …, w_j], where w_j = (μ_j, v_j, π_j) (j = 1,2, …, n).

Step 4. Construct the aggregated weighted IFDM.

In Step 4, the weights of criteria (W) and the aggregated IFDM are determined to the aggregated weighted IFDM which is constructed according to the following definition [19]:

()

R′ is a matrix composed with elements IFNs,

Step 5. Determine intuitionistic fuzzy positive and negative ideal solution.

In this step, the intuitionistic fuzzy positive ideal solution (IFPIS) and intuitionistic fuzzy negative ideal solution (IFNIS) have to be determined. Let J₁ and J₂ be benefit criteria and cost criteria, respectively. A^* is IFPIS and A⁻ is IFNIS. Then A^* and A⁻ are equal to

()

where

()

Step 6. Determine the separation measures between the alternative.

Separation between alternatives on IFS, distance measures proposed by Atanassov [63], Szmidt and Kacprzyk [64], and Grzegorzewski [65] including the generalizations of Hamming distance, Euclidean distance and their normalized distance measures can be used. After selecting the distance measure, the separation measures, and , of each alternative from IFPIS and IFNIS, are calculated:

()

Step 7. Determine the final ranking.

In the final step, the relative closeness coefficient of an alternative A_i with respect to the IFPIS A^* is defined as follows:

()

The alternatives were ranked according to descending order of

’s score.

3.2. DIFWA

The DIFWA method, proposed by Xu and Yager [33], is a suitable way to deal with problem in IFE. The procedure for DIFWA method has been given as follows.

Step 1. Utilize the DIFWA operator

()

to aggregate all the intuitionistic fuzzy matrix R(t_k) = (r_ij(t_k)) _m×n (k = 1,2, …, p) into a complex IFDM:

()

Step 2. Define as the IFPIS and the IFNIS, respectively, where α⁺ = (1,0, 0) (i = 1,2, …, m) are the m largest IFNs and α⁻ = (0,1, 0) (i = 1,2, …, m) are the m smallest IFNs. Furthermore, for convenience of depiction, we denote the alternative x_i (i = 1,2, …, n) by x_i = (r_i1, r_i2, …, r_im) ^T, i = 1,2, …, n.

Step 3. Calculate the distance between the alternative x_i and the IFIS and the distance between the largest native x_i and the IFNIS, respectively:

()

where r_ij = (μ_ij, v_ij, π_ij), i = 1,2, …, n, j = 1,2, …, m.

Step 4. Calculate the closeness coefficient of each alternative:

()

Since

()

then (3.13) can be rewritten as

()

Step 5. Rank all the alternatives x_i (1,2, …, n) according to the closeness coefficients c(x_i) (1,2, …, n), the greater the value c(x_i), the better the alternative x_i.

4. Case Study

In this section, we will describe how an IFT method was applied via an example of selection of the most appropriate projects. Criteria to be considered in the selection of projects are determined by the expert team from a construction group. In our study, we employ six evaluation criteria. The attributes which are considered here in assessment of P_i (i = 1,2, …, 6) are (1) C₁ is benefit and (2) C₂, …, C₆ are cost. The committee evaluates the performance of projects P_i (i = 1,2, …, 6) according to the attributes C_j (j = 1,2, …, 6), respectively. Criteria are mainly considered as follows

(i)
net present value (C₁),
(ii)
quality (C₂),
(iii)
duration (C₃),
(iv)
contractor’s rank (C₄),
(v)
contractor’s technology (C₅),
(vi)
contractor’s economic status (C₆).

Therefore, one cost criterion, C₁ and five benefit criteria, C₂, …, C₆ are considered. After preliminary screening, six projects P₁, P₂, P₃, P₄, P₅, and P₆ remain for further evaluation. A team of four DMs such as DM₁, DM₂, DM₃, and DM₄ has been formed to select the most suitable project.

Now utilizing the proposed IFT to prioritize these construction projects, the following steps were taken.

Degree of the DMs on group decision, shown in Table 1, and linguistic terms used for the ratings of the DMs and criteria, as Table 2, respectively.

Table 1. Linguistic term for rating DMs.

Linguistic terms	IFNs
Very important	(0.80, 0.10)
Important	(0.50, 0.20)
Medium	(0.50, 0.50)
Bad	(0.3, 0.50)
Very Bad	(0.20, 0.70)

Table 2. The importance of DMs and their weights.

	DM₁	DM₂	DM₃	DM₄
Linguistic terms	Very important	Medium	Important	Important
Weight	0.342	0.274	0.192	0.192

Construct the aggregated IFDM based on the opinions of DMs and the linguistic terms shown in Table 3.

Table 3. Linguistic terms for rating the alternatives.

Linguistic terms	IFNs
Extremely good (EG)	[1.00; 0.00; 0.00]
Very good (VG)	[0.85; 0.05; 0.10]
Good (G)	[0.70; 0.20; 0.10]
Medium bad (MB)	[0.50; 0.50; 0.00]
Bad (B)	[0.40; 0.50; 0.10]
Very bad (VB)	[0.25; 0.60; 0.15]
Extremely bad (EB)	[0.00, 0.90,0.10]

The ratings given by the DMs to six projects were shown in Table 4.

Table 4. The ratings of the projects.

Alternative	Criteria	DM₁	DM₂	DM₃	DM₄
P₁	C₁	VG	VG	G	G
	C₂	G	VG	MB	MB
	C₃	VG	G	B	VG
	C₄	VG	VG	G	G
	C₅	VG	VG	MB	G
	C₆	G	VG	MB	MB

P₂	C₁	G	VG	MB	B
	C₂	VG	VG	G	MB
	C₃	VG	VG	B	B
	C₄	VG	VG	MB	G
	C₅	G	G	G	G
	C₆	VG	VG	MB	B

P₃	C₁	VG	VG	G	VG
	C₂	VG	G	G	VG
	C₃	VG	G	VG	G
	C₄	VG	VG	VG	VG
	C₅	VG	VG	VG	VG
	C₆	VG	VG	VG	VG

P₄	C₁	MB	G	MB	VG
	C₂	G	VG	G	G
	C₃	MB	VG	G	G
	C₄	VG	G	VG	VG
	C₅	VG	VG	G	VG
	C₆	VG	VG	VG	VG

P₅	C₁	G	MB	MB	VB
	C₂	MB	B	B	VB
	C₃	B	G	MB	VG
	C₄	MB	B	VB	VG
	C₅	B	MB	VB	VG
	C₆	MB	VB	VB	MB

P₆	C₁	VG	VG	MB	MB
	C₂	G	VG	B	MB
	C₃	VG	VG	B	MB
	C₄	VG	VG	B	MB
	C₅	VG	VG	VB	VG
	C₆	VG	VG	G	MB

The aggregated IFDM based on aggregation of DMs’ opinions was constructed as follows:

()

The linguistic terms shown in Table 5 were used to rate each criterion. The importance of the criteria represented as linguistic terms was shown in Table 6.

Table 5. The linguistic terms for the importance of the criteria.

Linguistic terms	IFNs
Very good (VG)	[0.80; 0.10]
Good (G)	[0.50; 0.20]
Medium good (G)	[0.50; 0.50]
Very bad (VB)	[0.30; 0.50]
Bad (B)	[0.20; 0.60]

Table 6. The importance weight of the criteria.

Criteria	DM₁	DM₂	DM₃	DM₄
C₁	G	VG	VG	MB
C₂	VG	VG	VG	VG
C₃	MB	G	VG	MB
C₄	G	G	VG	G
C₅	G	VG	MB	G
C₆	MB	G	MB	VG

The opinions of DMs on criteria were aggregated to determine the weight of each criterion:

()

After the weights of the criteria and the rating of the projects were determined, the aggregated weighted IFDM was constructed as follows:

()

The net present value is cost criteria j₁ = {X₁}, and quality, duration, contractor’s rank, contractor’s technology, and contractor’s economic status are benefit criteria j₁ = {X₂, X₃, X₄, X₅}.

Then IFPIS and IFNIS were provided as follows:

()

Negative and positive separation measures based on normalized Euclidean distance for each project and the relative closeness coefficient were calculated in Table 7.

Table 7. Separation measures and the relative closeness coefficient of each project.

Alternatives	S^*	S⁻	C_i *
P₁	0.36	1.38	0.79
P₂	0.42	1.35	0.77
P₃	0.04	1.73	0.98
P₄	0.23	1.54	0.87
P₅	0.18	0.02	0.01
P₆	0.3	1.46	0.83

Six projects were ranked according to descending order of ’s. The result score is always the bigger the better. As visible in Table 6, project 3 has the largest score, and project 5 has the smallest score of the six projects which is ranked in the last pace. The projects were ranked as P₃ >P₄ >P₆ >P₁> P₂ > P₅. Project 3 was selected as appropriate project among the alternatives.

In the second part, we utilize the proposed DIFWA to prioritize these construction projects, and the following steps were taken.

First, utilize the DIFWA to aggregate all the IFDM R(t_k) into a complex IFDM R:

()

Denote the IFIS, IFNIS, and the alternatives by

()

and calculate the closeness coefficient of each alternative:

()

Rank all the projects according to the closeness coefficients.

The projects were ranked as C(P₃) > C(P₄) > C(P₆) > C(P₁) > C(P₂) > C(P₅). The greater value of C(X_i), the better alternative; thus the best alternative is also project 3.

5. Conclusion

The IFT and DIFWA have been emphasized in this paper which occurs in construction projects evaluation. In the evaluation process, the ratings of each project, given with intuitionistic fuzzy information, were represented as IFNs. The IFWA operator was used to aggregate the rating of DM. In project selection problem the project’s information and performance are usually uncertain. Therefore, the decision makers are unable to express their judgment on the project with crisp value, and the evaluations are very often expressed in linguistic terms. IFT and DIFWA are suitable ways to deal with MCDM because it contains a vague perception of DMs’ opinions. An actual life example in construction sector was illustrated, and finally the result is as follows Among 6 construction projects with respect to 6 criteria, after using these two methods, the best one is project 3 and project 4, project 6, project 1, project 2, project 5 will follow it, respectively. The presented approach not only validates the methods, as it was originally defined in Boran and Xu in a new application field that was the evaluation of construction projects, but also considers a more extensive list of benefit and cost-oriented criteria, suitable for construction project selection. Finally, the IFT and DIFWA methods have capability to deal with similar types of the same situations with uncertainty in MCDM problems such as ERP software selection and many other areas.

Acknowledgment

The author is very grateful to the anonymous referees for their constructive comments and suggestions that led to an improved version of this paper.

References

1 Dodangeh J., Mojahed M., and Yusuff R. B. M., Best project selection by using of Group TOPSIS method, Proceedings of the International Association of Computer Science and Information Technology (IACSIT-SC ′09), April 2009, 50–53, 2-s2.0-70449572541, https://doi.org/10.1109/IACSIT%2DSC.2009.119.
10.1109/IACSIT-SC.2009.119
Google Scholar
2 Wang J. and Hwang W. L., A fuzzy set approach for R&D portfolio selection using a real options valuation model, Omega. (2007) 35, no. 3, 247–257, 2-s2.0-33748255465, https://doi.org/10.1016/j.omega.2005.06.002.
10.1016/j.omega.2005.06.002
Web of Science® Google Scholar
3 Beaujon G. J., Marin S. P., and McDonald G. C., Balancing and optimizing a portfolio of R&D projects, Naval Research Logistics. (2001) 48, no. 1, 18–40, 1811049, ZBL0976.91030.
10.1002/1520-6750(200102)48:1<18::AID-NAV2>3.0.CO;2-7
Web of Science® Google Scholar
4 Rouyendegh B. D., The DEA and intuitionistic fuzzy TOPSIS approach to departments′ performances: a pilot study, Journal of Applied Mathematics. (2011) 2011, 16, 712194, https://doi.org/10.1155/2011/712194.
10.1155/2011/712194
Google Scholar
5 Mohanty R., Project selection by a multiple-criteria decision-making method: an example from a developing country, International Journal of Project Management. (1992) 10, no. 1, 31–38, 2-s2.0-0026579988.
10.1016/0263-7863(92)90070-P
Google Scholar
6 Mahmoodzadeh S., Shahrabi J., Pariazar M., and Zaeri M. S., Project selection by using fuzzy AHP and TOPSIS technique, International Journal of Human and Social Sciences. (2007) 1, no. 3, 333–338.
Google Scholar
7 Mohanty R. P., Agarval R., Choudhury A. K., and Tiwari M. K., Application of fuzzy analytical network process to R & D project selection, International Journal of Production Research. (2005) 43, no. 24, 5199–5216.
10.1080/00207540500219031
Web of Science® Google Scholar
8 Alidi A. S., Use of the analytic hierarchy process to measure the initial viability of industrial projects, International Journal of Project Management. (1996) 14, no. 4, 205–208, 2-s2.0-0030214584, https://doi.org/10.1016/0263%2D7863(95)00076%2D3.
10.1016/0263-7863(95)00076-3
Google Scholar
9 Al-Rashdan D., Al-Kloub B., Dean A., and Al-Shemmeri T., Environmental impact assessment and ranking the environmental projects in Jordan, European Journal of Operational Research. (1999) 118, no. 1, 30–45, 2-s2.0-0032679848, https://doi.org/10.1016/S0377%2D2217(97)00079%2D9.
10.1016/S0377-2217(97)00079-9
Web of Science® Google Scholar
10 Halouani N., Chabchoub H., and Martel J. M., PROMETHEE-MD-2T method for project selection, European Journal of Operational Research. (2009) 195, no. 3, 841–849, 2-s2.0-56349123919, https://doi.org/10.1016/j.ejor.2007.11.016.
10.1016/j.ejor.2007.11.016
Web of Science® Google Scholar
11 Abu-Taleb M. F. and Mareschal B., Water resources planning in the Middle East: application of the PROMETHEE V multicriteria method, European Journal of Operational Research. (1995) 81, no. 3, 500–511, 2-s2.0-0029270848.
10.1016/0377-2217(94)00007-Y
Web of Science® Google Scholar
12 Henriksen A. D. and Traynor A. J., A practical R&D project-selection scoring tool, IEEE Transactions on Engineering Management. (1999) 46, no. 2, 158–170, 2-s2.0-0032637622.
10.1109/17.759144
Web of Science® Google Scholar
13 Mavrotas G., Diakoulaki D., and Capros P., Combined MCDA-IP Approach for Project Selection in the Electricity Market, Annals of Operations Research. (2003) 120, no. 1–4, 159–170, https://doi.org/10.1023/A:1023382514182, 1990471, ZBL1038.90524.
10.1023/A:1023382514182
Web of Science® Google Scholar
14 Mavrotas G., Diakoulaki D., and Caloghirou Y., Project prioritization under policy restrictions. A combination of MCDA with 0-1 programming, European Journal of Operational Research. (2006) 171, no. 1, 296–308, 2-s2.0-28044468662, https://doi.org/10.1016/j.ejor.2004.07.069, ZBL1080.90051.
10.1016/j.ejor.2004.07.069
Web of Science® Google Scholar
15 Salo A., Gustafsson T., and Mild P., Prospective evaluation of a cluster Program for Finnish forestry and forest industries, International Transactions in Operational Research. (2004) 11, 139–154.
10.1111/j.1475-3995.2004.00447.x
Google Scholar
16 Kahraman C., Ruan D., and Doǧan I., Fuzzy group decision-making for facility location selection, Information Sciences. (2003) 157, no. 1–4, 135–153, 2-s2.0-0242365693, https://doi.org/10.1016/S0020%2D0255(03)00183%2DX.
10.1016/S0020-0255(03)00183-X
Web of Science® Google Scholar
17 Rouyendegh B. D. and Erol S., The DEA–FUZZY ANP department ranking model applied in Iran Amirkabir University, Acta Polytechnica Hungarica. (2010) 7, no. 4, 103–114.
Web of Science® Google Scholar
18 Kahraman Ç., Ruan D., and Tolga E., Capital budgeting techniques using discounted fuzzy versus probabilistic cash flows, Information Sciences. (2002) 142, no. 1–4, 57–76, 2-s2.0-0036571158, https://doi.org/10.1016/S0020%2D0255(02)00157%2D3.
10.1016/S0020-0255(02)00157-3
Web of Science® Google Scholar
19 Atanassov K. T., Intuitionistic fuzzy sets, Fuzzy Sets and Systems. (1986) 20, no. 1, 87–96, https://doi.org/10.1016/S0165%2D0114(86)80034%2D3, 852871, ZBL0631.03040.
10.1016/S0165-0114(86)80034-3
Web of Science® Google Scholar
20 De S. K., Biswas R., and Roy A. R., An application of intuitionistic fuzzy sets in medical diagnosis, Fuzzy Sets and Systems. (2001) 117, no. 2, 209–213, 2-s2.0-0035216480.
10.1016/S0165-0114(98)00235-8
Web of Science® Google Scholar
21 Szmidt E. and Kacprzyk J., Intuitionistic fuzzy sets in some medical applications, Computational Intelligence. Theory and Applications, 2001, 2206, 148–151, Lecture Notes in Computer Science.
10.1007/3-540-45493-4_19
Google Scholar
22 Szmidt E. and Kacprzyk J., A similarity measure for intuitionistic fuzzy sets and its application in supporting medical diagnostic reasoning, 3070, Proceedings of the 7th International Conference on Artificial Intelligence and Soft Computing (ICAISC ′04), June 2004, 388–393, Lecture Notes in Computer Science, 2-s2.0-9444274930.
Google Scholar
23 Hong D. H. and Choi C. H., Multicriteria fuzzy decision-making problems based on vague set theory, Fuzzy Sets and Systems. (2000) 114, no. 1, 103–113, 2-s2.0-0346054710.
10.1016/S0165-0114(98)00271-1
Web of Science® Google Scholar
24 Szmidt E. and Kacprzyk J., Using intuitionistic fuzzy sets in group decision making, Control and Cybernetics. (2002) 31, no. 4, 1037–1053, 2-s2.0-0037841591.
Web of Science® Google Scholar
25 Szmidt E. and Kacprzyk J., A consensus-reaching process under intuitionistic fuzzy preference relations, International Journal of Intelligent Systems. (2003) 18, no. 7, 837–852, 2-s2.0-0038487287, https://doi.org/10.1002/int.10119.
10.1002/int.10119
Web of Science® Google Scholar
26 Atanassov K. I., Pasi G., and Yager R., Intuitionistic fuzzy interpretations of multi-criteria multi-person and multi-measurement tool decision making, International Journal of Systems Science. (2005) 36, no. 14, 859–868, 2-s2.0-31444442863, https://doi.org/10.1080/00207720500382365.
10.1080/00207720500382365
Web of Science® Google Scholar
27 Li D. F., Multiattribute decision making models and methods using intuitionistic fuzzy sets, Journal of Computer and System Sciences. (2005) 70, no. 1, 73–85, https://doi.org/10.1016/j.jcss.2004.06.002, 2102063, ZBL1066.90052.
10.1016/j.jcss.2004.06.002
Web of Science® Google Scholar
28 Liu H. W. and Wang G. J., Multi-criteria decision-making methods based on intuitionistic fuzzy sets, European Journal of Operational Research. (2007) 179, no. 1, 220–233, 2-s2.0-33751331720, https://doi.org/10.1016/j.ejor.2006.04.009.
10.1016/j.ejor.2006.04.009
Web of Science® Google Scholar
29 Xu Z., Intuitionistic preference relations and their application in group decision making, Information Sciences. (2007) 177, no. 11, 2363–2379, 2-s2.0-33947202127, https://doi.org/10.1016/j.ins.2006.12.019.
10.1016/j.ins.2006.12.019
Web of Science® Google Scholar
30 Xu Z., Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making, Fuzzy Optimization and Decision Making. (2007) 6, no. 2, 109–121, https://doi.org/10.1007/s10700%2D007%2D9004%2Dz, 2333107, ZBL1158.03319.
10.1007/s10700-007-9004-z
CAS Web of Science® Google Scholar
31 Xu Z. S., Models for multiple attribute decision making with intuitionistic fuzzy information, International Journal of Uncertainty, Fuzziness and Knowlege-Based Systems. (2007) 15, no. 3, 285–297, https://doi.org/10.1142/S0218488507004686, 2334731.
10.1142/S0218488507004686
Web of Science® Google Scholar
32 Lin L., Yuan X. H., and Xia Z. Q., Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets, Journal of Computer and System Sciences. (2007) 73, no. 1, 84–88, https://doi.org/10.1016/j.jcss.2006.03.004, 2279033, ZBL1178.68541.
10.1016/j.jcss.2006.03.004
Web of Science® Google Scholar
33 Xu Z. and Yager R. R., Dynamic intuitionistic fuzzy multi-attribute decison making, International Journal of Approximate Reasoning. (2008) 48, no. 1, 246–262, https://doi.org/10.1016/j.ijar.2007.08.008, 2420670.
10.1016/j.ijar.2007.08.008
Web of Science® Google Scholar
34 Li D. F., Extension of the LINMAP for multiattribute decision making under Atanassov′s intuitionistic fuzzy environment, Fuzzy Optimization and Decision Making. (2008) 7, no. 1, 17–34, https://doi.org/10.1007/s10700%2D007%2D9022%2Dx, 2389085, ZBL1140.90430.
10.1007/s10700-007-9022-x
Web of Science® Google Scholar
35 Wei G. W., Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting, Knowledge-Based Systems. (2008) 21, no. 8, 833–836, 2-s2.0-54949099633, https://doi.org/10.1016/j.knosys.2008.03.038.
10.1016/j.knosys.2008.03.038
Web of Science® Google Scholar
36 Xu Z. and Cai X., Incomplete interval-valued intuitionistic fuzzy preference relations, International Journal of General Systems. (2009) 38, no. 8, 871–886, https://doi.org/10.1080/03081070903210630, 2590423, ZBL1177.90230.
10.1080/03081070903210630
Web of Science® Google Scholar
37 Li D. F., Wang Y. C., Liu S., and Shan F., Fractional programming methodology for multi-attribute group decision-making using IFS, Applied Soft Computing Journal. (2009) 9, no. 1, 219–225, 2-s2.0-53749097742, https://doi.org/10.1016/j.asoc.2008.04.006.
10.1016/j.asoc.2008.04.006
Web of Science® Google Scholar
38 Wei G. W., Some geometric aggregation functions and their application to dynamic multiple attribute decision making in the intuitionistic fuzzy setting, International Journal of Uncertainty, Fuzziness and Knowlege-Based Systems. (2009) 17, no. 2, 179–196, https://doi.org/10.1142/S0218488509005802, 2512737, ZBL1162.90485.
10.1142/S0218488509005802
Web of Science® Google Scholar
39 Xia M. and Xu Z., Some new similarity measures for intuitionistic fuzzy value and their application in group decision making, Journal of Systems Science and Systems Engineering. (2010) 19, no. 4, 430–452, 2-s2.0-78650418032, https://doi.org/10.1007/s11518%2D010%2D5151%2D9.
10.1007/s11518-010-5151-9
Web of Science® Google Scholar
40 Xu Z. and Hu H., Projection models for intuitionistic fuzzy multiple attribute decision making, International Journal of Information Technology and Decision Making. (2010) 9, no. 2, 267–280, 2-s2.0-77951672266, https://doi.org/10.1142/S0219622010003816.
10.1142/S0219622010003816
Web of Science® Google Scholar
41 Xu Z. and Cai X., Nonlinear optimization models for multiple attribute group decision making with intuitionistic fuzzy information, International Journal of Intelligent Systems. (2010) 25, no. 6, 489–513, 2-s2.0-77954554038, https://doi.org/10.1002/int.20409.
10.1002/int.20409
Web of Science® Google Scholar
42 Tan C. and Chen X., Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making, Expert Systems with Applications. (2010) 37, no. 1, 149–157, 2-s2.0-70349466357, https://doi.org/10.1016/j.eswa.2009.05.005.
10.1016/j.eswa.2009.05.005
Web of Science® Google Scholar
43 Xu Z., A deviation-based approach to intuitionistic fuzzy multiple attribute group decision making, Group Decision and Negotiation. (2010) 19, no. 1, 57–76, 2-s2.0-77952741966, https://doi.org/10.1007/s10726%2D009%2D9164%2Dz.
10.1007/s10726-009-9164-z
PubMed Web of Science® Google Scholar
44 Park J. H., Park I. Y., Kwun Y. C., and Tan X., Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment, Applied Mathematical Modelling. (2011) 35, no. 5, 2544–2556, https://doi.org/10.1016/j.apm.2010.11.025, 2763882, ZBL1217.90123.
10.1016/j.apm.2010.11.025
Web of Science® Google Scholar
45 Chen T. Y., Wang H. P., and Lu Y. Y., A multicriteria group decision-making approach based on interval-valued intuitionistic fuzzy sets: a comparative perspective, Expert Systems with Applications. (2011) 38, no. 6, 7647–7658, 2-s2.0-79951576510, https://doi.org/10.1016/j.eswa.2010.12.096.
10.1016/j.eswa.2010.12.096
Web of Science® Google Scholar
46 Xia M. and Xu Z., Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment, Information Fusion. (2011) 13, 31–47, 2-s2.0-78650860365, https://doi.org/10.1016/j.inffus.2010.12.001.
10.1016/j.inffus.2010.12.001
Web of Science® Google Scholar
47 Li D. and Cheng C., New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions, Pattern Recognition Letters. (2002) 23, no. 1–3, 221–225, 2-s2.0-0036132355, https://doi.org/10.1016/S0167%2D8655(01)00110%2D6.
10.1016/S0167-8655(01)00110-6
Web of Science® Google Scholar
48 Liang Z. and Shi P., Similarity measures on intuitionistic fuzzy sets, Pattern Recognition Letters. (2003) 24, no. 15, 2687–2693, 2-s2.0-0041328307, https://doi.org/10.1016/S0167%2D8655(03)00111%2D9.
10.1016/S0167-8655(03)00111-9
Web of Science® Google Scholar
49 Hung W. L. and Yang M. S., Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance, Pattern Recognition Letters. (2004) 25, no. 14, 1603–1611, 2-s2.0-4644256932, https://doi.org/10.1016/j.patrec.2004.06.006.
10.1016/j.patrec.2004.06.006
Web of Science® Google Scholar
50 Wang W. and Xin X., Distance measure between intuitionistic fuzzy sets, Pattern Recognition Letters. (2005) 26, no. 13, 2063–2069, 2-s2.0-24344448274, https://doi.org/10.1016/j.patrec.2005.03.018.
10.1016/j.patrec.2005.03.018
Web of Science® Google Scholar
51 Zhang C. and Fu H., Similarity measures on three kinds of fuzzy sets, Pattern Recognition Letters. (2006) 27, no. 12, 1307–1317, 2-s2.0-33646805776, https://doi.org/10.1016/j.patrec.2005.11.020.
10.1016/j.patrec.2005.11.020
Web of Science® Google Scholar
52 Vlachos I. K. and Sergiadis G. D., Intuitionistic fuzzy information—applications to pattern recognition, Pattern Recognition Letters. (2007) 28, no. 2, 197–206, 2-s2.0-33750818700, https://doi.org/10.1016/j.patrec.2006.07.004.
10.1016/j.patrec.2006.07.004
Web of Science® Google Scholar
53 Boran F. E., Genç S., Kurt M., and Akay D., A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method, Expert Systems with Applications. (2009) 36, no. 8, 11363–11368, 2-s2.0-67349223299, https://doi.org/10.1016/j.eswa.2009.03.039.
10.1016/j.eswa.2009.03.039
Web of Science® Google Scholar
54 Kavita, Yadav S. P., and Kumar S., A multi-criteria interval-valued intuitionistic fuzzy group decision making for supplier selection with TOPSIS method, Rough Sets, Fuzzy Sets, Data Mining and Granular Computing, 2009, 5908, 303–312, 2-s2.0-76649087690, https://doi.org/10.1007/978%2D3%2D642%2D10646%2D0_37.
10.1007/978-3-642-10646-0_37
Google Scholar
55 Ye F., An extended TOPSIS method with interval-valued intuitionistic fuzzy numbers for virtual enterprise partner selection, Expert Systems with Applications. (2010) 7, no. 10, 7050–7055, 2-s2.0-77950788569, https://doi.org/10.1016/j.eswa.2010.03.013.
10.1016/j.eswa.2010.03.013
Google Scholar
56 Boran F. E., Genç S., and Akay D., Personnel selection based on intuitionistic fuzzy sets, Human Factors and Ergonomics In Manufacturing. (2011) 21, no. 5, 493–503.
10.1002/hfm.20252
Web of Science® Google Scholar
57 Boran F. E., Boran K., and Menlik T., The evaluation of renewable energy technologies for electricity generation in Turkey using intuitionistic fuzzy TOPSIS, Energy Sources, Part B. (2012) 7, 81–90.
10.1080/15567240903047483
Web of Science® Google Scholar
58 Boran F. E., An integrated intuitionistic fuzzy multi criteria decision making method for facility location selection, Mathematical and Computational Applications. (2011) 16, no. 2, 487–496, 2-s2.0-79952926815.
10.3390/mca16020487
Google Scholar
59 Wang P., QoS-aware web services selection with intuitionistic fuzzy set under consumer′s vague perception, Expert Systems with Applications. (2009) 36, no. 3, 4460–4466, 2-s2.0-58349102739, https://doi.org/10.1016/j.eswa.2008.05.007.
10.1016/j.eswa.2008.05.007
Web of Science® Google Scholar
60 Shu M. H., Cheng C. H., and Chang J. R., Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly, Microelectronics Reliability. (2006) 46, no. 12, 2139–2148, 2-s2.0-33749117530, https://doi.org/10.1016/j.microrel.2006.01.007.
10.1016/j.microrel.2006.01.007
Web of Science® Google Scholar
61 Gerogiannis V. C., Fitsillis P., and Kameas A. D., Using combined intuitionistic fuzzy set-Topsis method for evaluating project and portfolio management information system, IFIP Inernational Federation for Information Processing. (2011) 364, 67–81.
Google Scholar
62 Xu Z., Intuitionistic fuzzy aggregation operators, IEEE Transactions on Fuzzy Systems. (2007) 15, no. 6, 1179–1187, 2-s2.0-37249067095, https://doi.org/10.1109/TFUZZ.2006.890678.
10.1109/TFUZZ.2006.890678
Web of Science® Google Scholar
63 Atanassov K. T., Intuitionistic Fuzzy Sets, 1999, 35, Physica-Verlag, Heidelberg, Germany, Studies in Fuzziness and Soft Computing, 1718470.
10.1007/978-3-7908-1870-3
Google Scholar
64 Szmidt E. and Kacprzyk J., Distances between intuitionistic fuzzy sets, Fuzzy Sets and Systems. (2000) 114, no. 3, 505–518, https://doi.org/10.1016/S0165%2D0114(98)00244%2D9, 1775286, ZBL0961.03050.
10.1016/S0165-0114(98)00244-9
Web of Science® Google Scholar
65 Grzegorzewski P., Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff metric, Fuzzy Sets and Systems. (2004) 148, no. 2, 319–328, https://doi.org/10.1016/j.fss.2003.08.005, 2100203, ZBL1056.03031.
10.1016/j.fss.2003.08.005
Web of Science® Google Scholar

Citing Literature

All articles

Evaluating Projects Based on Intuitionistic Fuzzy Group Decision Making

Abstract

1. Introduction