The problem considered is an investigation of the possible collapse of the roof between the pillar next to be mined in secondary coal mining and the first line of pillar remnants called snooks. The roof rock between the pillar, which is the working face, and the snook is modelled as an Euler-Bernoulli beam acted on at each end by a horizontal force and by its weight per unit length. The beam is clamped at the pillar and simply supported (hinged) at the snook. The dimensionless differential equation for the beam and the boundary conditions depend on one dimensionless number B. We consider the range of values of B before the displacement and curvature first become singular at B = B₁. The model predicts that for all practical purposes, the beam will break at the clamped end at the pillar. The failure of the beam for values of B greater than B₁ is investigated computationally.

1. Introduction

We consider the challenge posed by coal mine pillar extraction [1, 2]. Secondary mining involves revisiting a mine and extracting coal from the pillars. The mining of these pillars commences from the area furthest away from the point of entry of the mine. This exercise involves cutting the existing pillars into smaller pillars called snooks. As each section is mined, the roof must collapse in a controlled manner in order to pose no safety risk to those miners operating underground. We analyse the behaviour of the roof of the mine between the pillar next to be mined and the first line of snooks. This is the work area and must be safe for the miners.

2. Model

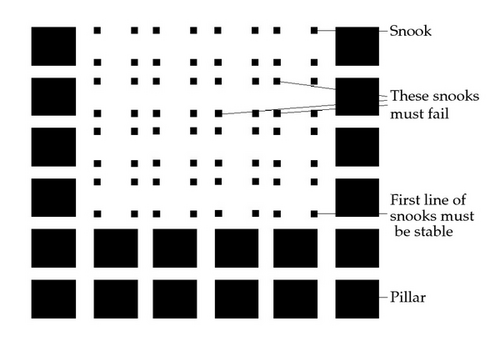
In Figure 1, a mining panel in shown prior to pillar extraction. The tunnels are excavated in coal which are approximately 5 m to 7 m wide. They are excavated in a fixed pattern crossing at right angles creating a checker board layout. The coal between the tunnels forms the pillars which support the overburden rock. The width of the pillars is approximately 10 m to 20 m wide and is a function of the depth of the mine. The height of the tunnels ranges from 3 m to 4 m. Secondary mining is carried out in two stages. In the initial stage, approximately 5 to 10 pillars are removed and the roof is left to collapse. This stage is modelled in [2]. Following this, adjacent pillars are mined and smaller sections are left to collapse. The purpose of this paper is to model the second stage in the extraction process. Figure 2 shows the snooks after pillar extraction. The pillars are cut to leave four snooks, approximately 2 m, one at each corner. The snooks have to be small enough to fail when the miners are a safe distance (about the width of a pillar) from the working face but they have to be large enough to be stable right next to the unmined pillars.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A mining panel showing the pillars before pillar extraction. Reproduced with permission from N. van der Merwe.

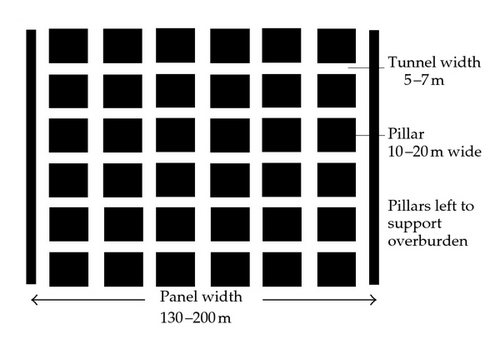
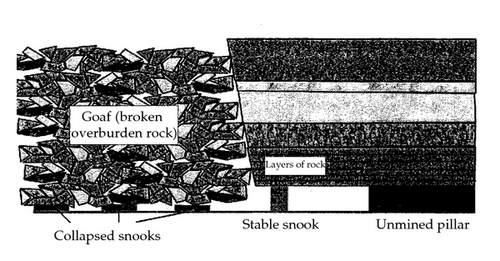
The roof consists of horizontal layers of rock of approximate thickness 0.5 m to 20 m, as shown in Figure 3. The Euler-Bernoulli beam equation can be used to describe the horizontal layers of rock in the roof. The use of the Euler-Bernoulli beam equation assumes that the roof is thin compared with its horizontal extent and that only the horizontal direction is important. The horizontal extent of the beam is the distance from the next pillar to be mined to the first line of snooks which is the width of the tunnel and is approximately 6 m. The ratio of the thickness of the beam to its length ranges from about 0.1 to about 3 and thus for the theory to apply the thickness of the beam should not exceed 2 m. The width of the mining panel ranges from about 130 m to 200 m. If we take the width of the mining panel as the width of the beam then the ratio of the length of the beam to its width varies from about 0.05 to 0.03. Dependence of the variables in the direction of the width of the beam can therefore be neglected. The use of the Euler-Bernoulli beam is therefore justified for a beam of thickness less than about 2 m.

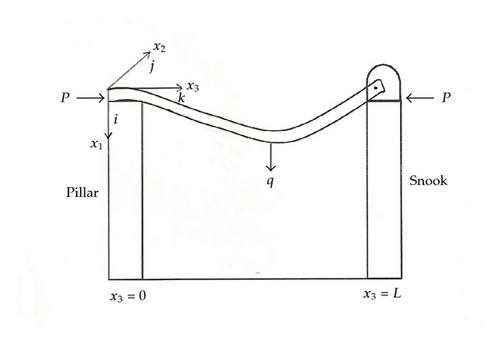
In this paper we will investigate if roof collapse can occur between the next pillar to be mined and the first line of snooks when these snooks are stable and do not fail. In order to achieve this, we consider the roof of the mine to be clamped at a pillar while at the adjacent snook, the roof is simply supported or hinged. We consider the roof to be simply supported at the snook since as secondary mining takes place, disturbances in the rock mass and also the roof collapse due to the failure of the neighbouring snooks could change the roof structure in the region where the snooks support the beam [3]. We model this by assuming that at the snook the beam is no longer clamped and use instead that the beam is simply supported or hinged at the snook. We also consider the behaviour of this small section of the roof when a disturbance, such as a seismic event, causes a sudden increase in the horizontal force acting at each end of the section of the roof.

An analysis of the problem where both ends of the beam are clamped is presented in [2]. The beam number B, which occurred in the dimensionless Euler-Bernoulli beam equation, was defined in [2] as follows:

()

where P is the horizontal axial force applied to the ends of the beam, L is the length, E is the Young’s modulus of the beam, and I is a second moment of the cross-sectional area of the beam. The beam number was the only dimensionless parameter in the problem. This number has arisen before in the literature, for example in [4], but no name was assigned to it. The displacement became singular when B = 2nπ where n = 1,2, 3…. The magnitude of the displacement was greatest at the centre of the beam for 0 < B < 2π due to the symmetry of the problem. For 0 < B < 2π the magnitude of the curvature was greatest at the endpoints of the beam and thus the beam collapsed at these points when the tensile strength of the beam was exceeded. The problem of one end clamped and one simply supported is not symmetric. Our task is to solve and analyse this problem and to compare it with the problem with both ends clamped.

Previous work on roof failure due to the failure of snooks is reviewed in [5]. Useful texts are [6–9].

3. Derivation of the Differential Equation

The combined beam and strut is shown in Figure 4. We will use the notation and conventions of Segal and Handelman [10]. The coordinate axes are defined in terms of the undeformed beam. The x₁- and x₂-axes are along the axes of principle moments of inertia of the cross-section of the beam with the x₁-axis vertically downwards. The x₃-axis is horizontal and passes through the centroid of each cross-section. The origin of the coordinate system is at the centroid of the cross-section of the left end of the beam. Unit vectors, i, j, and k are directed along each coordinate axis. For simplicity, we denote x₃ by x.

An outline of the derivation of the differential equation for the Euler-Bernoulli beam when both ends are clamped is given in [2, 10]. The potential energy V of an elastic beam of length L and Young’s modulus E is given by the following:

()

where w(x) is the displacement of the beam from the horizontal position x vertically downwards in the direction of i, I is the second moment of area about the x₂-axis, q(x) is the magnitude of the body force per unit length, s(x) is the magnitude of the applied surface traction per unit length in the direction of i, and P is the horizontal force acting at each end of the beam. We assume that the simple support or hinge can oppose an axial force thus disallowing any axial motion. The nonlinear strain tensor is used in part of the derivation of V(w) in [10].

The derivation of the beam equation depends on the boundary conditions. We show that the boundary conditions for the present problem yield the same beam equation as in [2] and thus the only difference between the two problems is their boundary conditions. The boundary conditions with one end clamped and the other end simply supported are as follows:

()

At equilibrium, the potential energy is at an extremum. In order to impose this condition we let

()

where ϵ is a constant parameter. Since w(x) satisfies boundary conditions (3.2) for all ϵ it implies that w₀(x) and w₁(x) must separately satisfy (3.2). Thus we have,

()

giving that, at equilibrium,

()

We use integration by parts and the boundary conditions to deduce the following results:

()

Using (3.6) we can rewrite (3.5) as

()

Since (3.7) holds for arbitrary w₁(x), we can deduce that

()

In our model the roof is made of horizontal layers of rock each acting as a beam. The horizontal force P acting on each end of the beam arises as a result of the compressive stresses due to the rock mass above. The quantity q is the weight per unit length of the beam which we assume is constant. The quantity s is the magnitude of the applied normal surface traction per unit length due to the transfer of stresses from the adjoining layers. We assume that s is constant. The displacement depends on the weight and on the applied normal surface traction in the same way. We will therefore denote the combined forces, s and q, simply by q. The above derivation and in [2] differ from that of Segal and Handelman [10] by the inclusion of q(x) and s(x) in the analysis. Also, in [10], the boundary conditions were as follows:

()

while in [2], the boundary conditions were as follows:

()

We see that the Euler-Bernoulli beam equation remains valid for the boundary conditions used in this paper. Equation (3.8) is now written in dimensionless form. Define [2]:

()

where S is the characteristic displacement. Equation (3.8) becomes

()

where the beam number B is defined by (2.1). The boundary conditions, (3.2), when expressed in dimensionless variables become

()

The bending moment M is [10] as follows:

()

where, since it is assumed that the displacement is sufficiently small that linear theory applies [10],

()

Define [2]:

()

Then

()

and we will refer to

as both the bending moment and curvature of the beam. The overhead bar will be suppressed in the rest of the paper to keep the notation simple.

4. Mathematical Solution

Consider the model of the roof rock between a pillar at x = 0 which is the working face and a snook at x = 1 described by an Euler-Bernoulli beam with end x = 0 clamped and end x = 1 simply supported or hinged. The displacement w(x) satisfies the differential equation

()

subject to the boundary conditions

()

The solution for w(x) is

()

provided that B does not satisfy

()

We can rewrite (4.4) as follows:

()

Equations (4.4) and (4.5) are plotted in Figures 5 and 6. The first five roots of (4.4) and (4.5) are

()

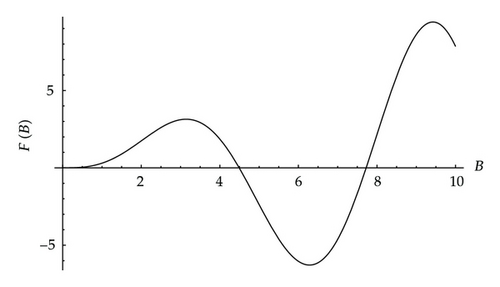
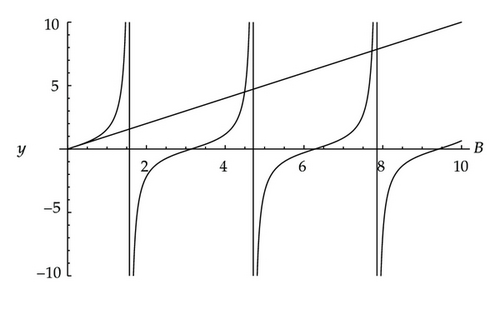
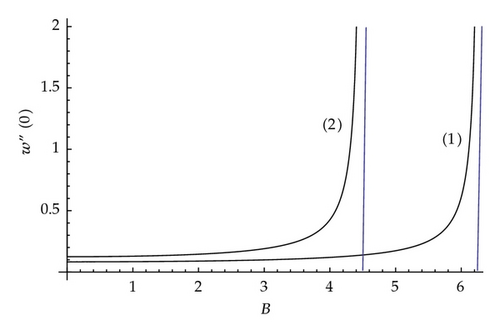
At these values of B, the displacement becomes infinite. Since B = 4.4934 is the first nonzero value of B for which the displacement becomes singular, our primary concern is in the interval 0 < B < 4.4934. In the next section, we discuss the solution (4.3) for the displacement and calculate the curvature of the beam which determines the location at which the beam will break.

For a beam with both ends clamped [2], the displacement becomes singular for B = 2nπ where n = 1,2, 3, …. Comparing the first points at which the displacement becomes singular in the two models, we note that 4.4934 < 2π = 6.2832. Small displacements and small derivatives are used in the derivation of the Euler-Bernoulli beam equation. The theory therefore breaks down in the neighbourhood of the points x = B_n where the curvature has singular behaviour. A full nonlinear theory would need to be used in these regions. However, the beam will break when its tensile strength is exceeded which could be well before the singularities in the curvature are reached.

5. Analysis of the Results

Graphs of the displacement w(x) for values of the beam number, B, in the range 0 < B < 4.4934 are shown in Figure 7. The displacement has two stationary points which are located at x = 0 and at an interior point.

Consider first the beam for small values of B. The asymptotic expansion of w(x) as B → 0 is given by the following:

()

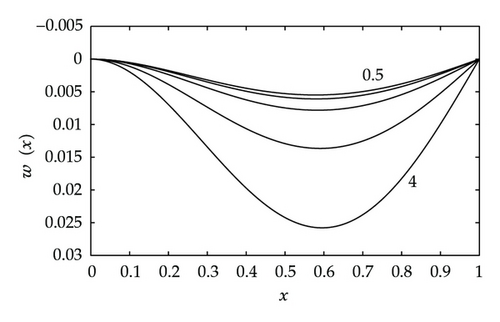
The displacement is nonzero when B = 0 because of the weight per unit length, q, acting on the beam. Graphs of the displacement w(x) for small values of B are presented in Figure 8. From the graphs, we can see that (5.1) is a good approximation for the displacement for B ≤ 0.9.

Denote by x₀ the point of maximum displacement of the beam. In order to estimate x₀ for small B, consider, from (5.1),

()

The root of the quadratic equation

()

in the range 0 < x < 1 is x = 0.578 and therefore,

()

The root of

()

in the range 0 < x < 1 is x = 0.594 which is only 2.77% larger than 0.578. The maximum turning points of the curves in Figure 10 are all close to the zero order in B value. This shows that (5.4) is a good approximation of x₀ for small values of B. Substituting (5.4) into (5.1) gives

()

which from Figures 7 and 8 is a good approximation for B ≤ 0.5. In comparison, for a beam with clamped ends, from symmetry, the magnitude of the deflection is a maximum at x₀ = 0.5 for 0 < B < 2π.

In order to gain insight into the possible failure of the beam, we need to determine the point at which the beam is under maximum stress. We assume that this is the point at which the magnitude of the curvature is greatest. The dimensionless curvature of the beam is given by the following:

()

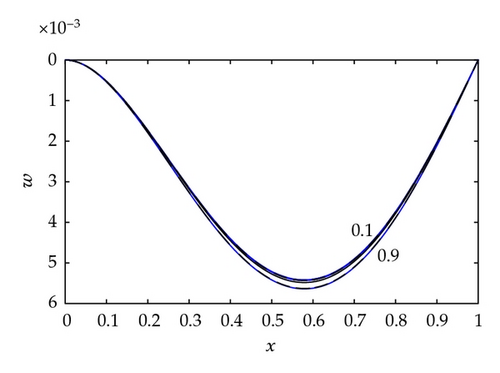
Graphs of the magnitude of the curvature for a range of values B < B₁ are given in Figure 9.

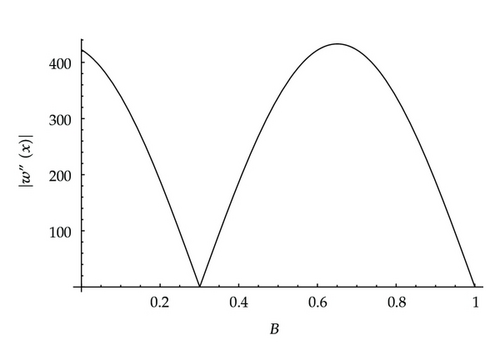
The curvature vanishes at x = 1 because the end x = 1 is simply supported. Denote by x₁ the position of the local maximum of the magnitude of the curvature when 0 < x < 1. Since the sign of the curvature at x = 0 is opposite to that at x = x₁, the curvature must vanish at a point, say x₂, where 0 < x₂ < x₁. We can deduce from Figure 9 that x₂ does not change significantly as B is increased. For the range of values used in Figure 9, the magnitude of the curvature at x = 0 is greater than at x = x₁. We will investigate later as to whether this is always the case.

Consider first the curvature for small values of B. The asymptotic expansion of (5.7) as B → 0 is given by the following:

()

To zero order in B, the zeros of the curvature occur at x = 1 and x = 1/4 and therefore,

()

The root of the cubic equation

()

in the range 0 < x < 1 is x = 0.287 which explains why x₂ does not greatly depend on B. The expansions are in good agreement with Figure 9.

We now consider the turning point x = x₁ of the curvature. From (5.7),

()

which vanishes for x = x₁, where

()

We now examine R, the absolute value of the ratio of the curvature at x = 0 to the curvature at x = x₁ as follows:

()

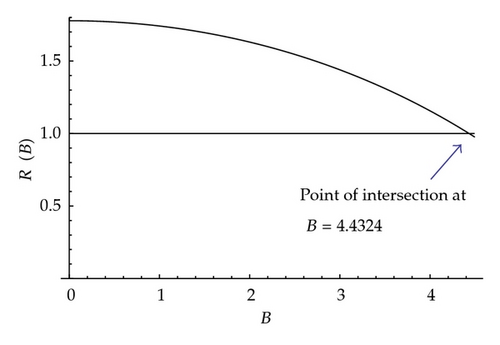
For the range of values of B considered in Figure 9, R(B) > 1. However, as B approaches the first singular value B = B₁ = 4.4934, the ratio R approaches and may exceed unity. This is illustrated in Figure 10 where B = 4.4930. We now investigate analytically the ratio R(B) for 0 ≤ B ≤ B₁.

Consider first the asymptotic behaviour as B → 0. Now

()

and therefore, from (5.12)

()

The value x₁ = 0.625 for small B is consistent with the graphs in Figure 9. Also, from (5.8), as B → 0,

()

and therefore,

()

A more detailed calculation yields the following result

()

so that R(B) decreases initially as B increases.

Consider next the limit as B → B₁. The curvature w^′′(x), given by (5.7), may be expressed in terms of F(B), P(B), and Q(B) as follows:

()

Then,

()

Also, since x₁ is defined by (5.12),

()

and therefore,

()

Hence,

()

Now at B = B₁, F(B₁) = 0 and therefore, sin⁡B₁ = B₁cos⁡B₁. Thus,

()

and hence

()

Thus, R(B₁) < 1. Also, using (5.12) and (5.24), we find that in the limit B = B₁, x₁ is given by the following:

()

Since B₁ = 4.4934, it follows that

()

and that

()

The graph of R(B) against B for 0 ≤ B < B₁ is presented in Figure 11. The analytical results for B → 0 and B → B₁ agree with the graph. In comparison when the two ends of the beam are clamped, R(B) > 1 for 0 ≤ B < B₁ and R(B₁) = 1, where B₁ = 2π.

6. Numerical Estimates

Consider first the beam number B defined by (2.1). The total horizontal force P acting on each end section is given by [2, 9, 10] the following:

()

where H is the depth of the mine below the surface of the earth, ρ is the average density of the rock from the surface of the earth to the depth H, b is the breadth of the roof beam, h is the thickness of the beam, and k is the lateral stress coefficient. The lateral stress coefficient is a function of the rock properties. The value k = 0 corresponds to a material that is completely solid while k = 1 corresponds to a fluid in which the pressure is isotropic. Some models can predict values of k > 1 and that k decreases with depth [7]. For the shallow coal mines which we will consider, we will take k = 2 [11]. The second moment of area about the x₂-axis is [2]

()

The beam number (2.1) becomes

()

For a beam with one end clamped and the other end simply supported, the displacement and curvature become infinite first at B = B₁ = 4.4934. Thus we obtain the upper limit L_c for the length that a beam can have without collapsing:

()

As the beam becomes more fractured with time the Young’s modulus E will decrease and L_c will decrease.

When both ends of the beam are clamped, B₁ = 2π and the ratio of the maximum length L_c(2) when one end is clamped and one is simply supported, to the maximum length L_c(1) when both ends are clamped is

()

The critical length L_c(1) describes the initial stage of the process of pillar extraction when several pillars are removed and the roof is left to collapse, while L_c(2) models the second stage when adjacent pillars are mined and smaller sections of the roof are left to collapse. We see that L_c(2) < L_c(1) which is consistent with the two models.

We consider a beam made of sandstone. We use the following estimates:

()

Table 1 summarizes numerical estimates for L_c for a beam with one end clamped and the other simply supported. In a coal mine the distance between the pillars ranges from 5 m and 7 m. When the bending moment or curvature exceeds the tensile strength of the beam the roof will collapse. This may occur for beam lengths L less than L_c since L_c provides only an upper limit on the length of the beam for collapse.

Table 1. Critical length L_c.

h(m)	H = 120 m L_c(m)	H = 500 m L_c(m)
0.1	9.26	4.54
0.2	18.53	9.08
0.3	27.80	13.62
0.4	37.06	18.16
0.5	46.33	22.7
0.6	55.60	27.23
0.7	64.86	31.77
0.8	74.12	36.31
0.9	83.39	40.85
1	92.65	45.39

The axial force P may experience a sudden increase due to a seismic event which could last for a short time. Using (2.1), the upper limit for the length, L_c, can be written as follows:

()

If L_c is reduced below about 6 m due to an increase in P then a roof collapse may occur.

We now compare the effect of hinged and clamped supports at the snook at x = 1 on the curvature at the pillar at x = 0. When both ends of the beam are clamped [2],

()

When the end x = 0 is clamped and the end x = 1 is simply supported (hinged), from (5.7) and (5.8),

()

Thus,

()

In Figure 12 the graphs of and are plotted against B. We see that when the end x = 1 is simply supported the curvature at x = 0 is greater for a given value of B than when it is clamped. The tensile strength of the beam will be exceeded at the end x = 0 for lower values of B when the end x = 1 is simply supported than when it is clamped. The simply supported boundary condition has the effect of increasing the bending moment at the end x = 0 and causing the beam to break at x = 0 for lower values of B.

7. Values of the Beam Number B Greater Than B₁

A graph of the magnitude of the curvature of the beam at the end x = 0, plotted against B, is given in Figure 13. It divides the values of B into the intervals,

()

where B₁, B₂, B₃,… are the values at which the displacement and curvature become infinite. We have only considered the first interval I₁. Since, from (2.1), we see that the beam number B is proportional to L and P^(1/2) the value of B would increase if either L or P were to increase. The length of the beam increases by a finite amount when a snook fails. In the second stage of the pillar extraction process, small sections of the mine collapse but if the snooks are too strong they will support a longer section of the roof which will form a beam and collapse when the snooks fail. Another way in which B could increase suddenly is due to a seismic event which may produce a discontinuous increase in P which could last for a short period of time.

Consider first the displacement. The displacement for values of B in the first interval, I₁, was considered in Figure 7. In Figure 14 graphs of the displacement for representative values of B in the intervals, I₁ to I₆, are presented. We see that as B increases through the intervals the number of turning points increases and that the displacement can take negative values beyond interval I₁. The amplitude of the displacement will depend on how close B is to the singular end points of the interval.

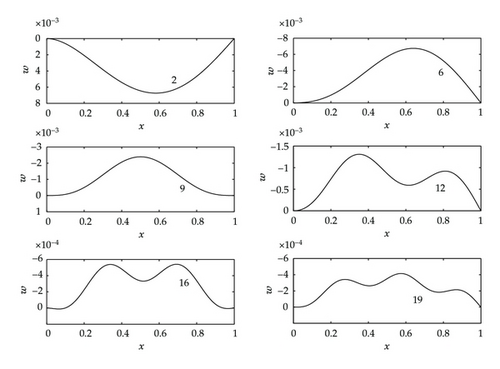
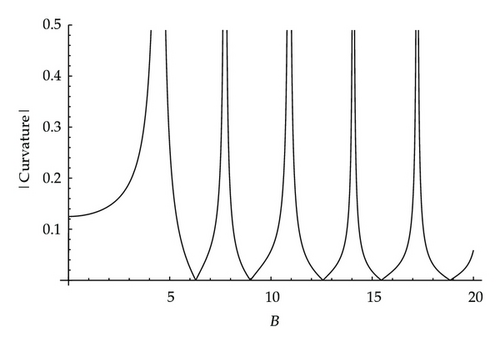
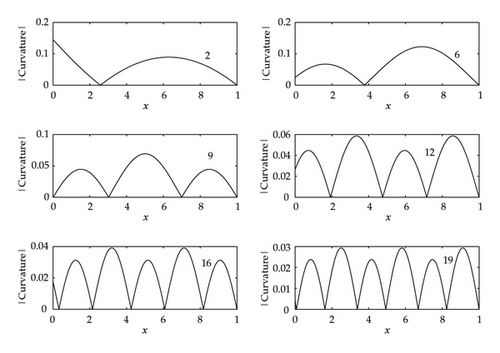
Consider next the magnitude of the curvature. In Figure 9 graphs of the magnitude of the curvature were plotted against x for values of B in the first interval I₁. In Figure 15, graphs of the magnitude of the curvature are plotted for the same representative values used to plot the displacement in Figure 14. For the values of B and n considered, the number of local maxima of the magnitude of the curvature in the nth interval I_n is n. The greatest local maximum is not at the end x = 0 but at interior points. There may be several points for which the magnitude of the curvature has the maximum value. If the bending moment exceeds the tensile strength the beam will break at these interior points. The magnitude of the curvature depends on how close B is to the singular endpoints of the interval. Since B is proportional to the length of the beam L we see from Figure 13 that if the value of B is in the range outside of B₁ then a longer beam could be less susceptible to failure than a shorter beam. This could be associated with the beam taking on a higher mode of bending. We see from Figure 14 that the displacement can be negative. For this to be possible in practice the beam would have to be detached sufficiently from the layers above.

8. Conclusions

We investigated the possible roof collapse between the next pillar to be mined and the first line of snooks by modelling the roof as an Euler-Bernoulli beam. The beam was simply supported (hinged) at the snook and clamped at the pillar which was the working face. The model contained one dimensionless number—the beam number B.

Numerical estimates obtained for the critical length L_c are comparable to the expected distance between pillars which in a coal mine is 5–7 m thus making the model credible. The model also predicts that the roof may collapse at the clamped end at the pillar for 0 < B < 4.4324. For the range 4.4324 < B < B₁ = 4.4934, the model predicts that the roof may collapse at an interior point closer to the snook than to the pillar where the magnitude of the curvature attains its maximum value. However, this range contributes only 1.36 percent of the range [0, B₁] and since it is likely that the threshold of the stress would have been exceeded for values of the beam number below B = 4.4324, for all practical purposes, the beam will break at the clamped end if the threshold of its stress is exceeded. It will therefore break at the pillar which is the working face. However, the model showed that it is not necessary for the beam to break at the clamped end. The beam may break at interior points. In I₁, the interior point is unique for a given value of B. Other boundary conditions would need to be considered and analyzed in order to determine whether the beam can collapse at an interior point for practical values of B.

From Figure 12 we deduced that a beam which is simply supported (hinged) at the snook produces a larger bending moment at the pillar (where it is clamped) than a beam which is clamped at the snook. The beam will break at a lower value of the beam number when it is hinged at the snook.

The displacement and curvature become infinite at the zeros of F(B) defined by (4.4) which divides the value of B into intervals. We considered mainly the first interval 0 ≤ B ≤ B₁. However, as the snooks fail B can increase discontinuously by finite amounts and may take values in the higher intervals. A preliminary computational investigation was undertaken of the displacement and curvature for values of B in these intervals. It was found that the displacement can take negative values. In the nth interval the magnitude of the curvature had n local maxima. The maximum value of the magnitude of the curvature did not in general occur at the pillar but occurred instead at interior points. If the tensile strength of the beam is exceeded the beam could break at several interior points.

In practice, roof bolts are installed [12].

Acknowledgments

The problem of pillar extraction in coal mines was submitted to the Mathematics in Industry Study Group 2011 (MISG) at the University of the Witwatersrand, Johannesburg. The author thanks the referees for their valuable comments which improved this paper greatly. The author thanks Matthew Woolway, University of the Witwatersrand, Johannesburg, for assisting in creating the diagrams. The author would like to express gratitude and appreciation to Professor Nielen van der Merwe and Dr. Halil Yilmaz of the School of Mining Engineering, University of the Witwatersrand, for submitting the problem. The author would particularly like to acknowledge that she has profited greatly from the discussions held with Professor Nielen van der Merwe. The author would like to acknowledge Professor Colin Please of the University of Southhampton, England, who formulated the model for pillar extraction and roof collapse at the MISG. The author thanks Professor David Mason for his valuable comments, advice, and encouragement while she was writing this paper.

References

1 van der Merwe J. N., Fundamental analysis of the interaction between overburden behaviour and snook stability in coal mines, Journal of the South African Institute of Mining and Metallurgy. (2005) 105, 63–73.
Google Scholar
2 Please C., Mason D. P., Khalique C. M., Ngnotchouye J. M. T., van der Merwe J. N., and Yilmaz H., Coal mine pillar extraction, Submitted to International Journal of Rock Mechanics and Mining Sciences.
Google Scholar
3 van der Merwe N., Private communication, 2012.
Google Scholar
4 Kimball C. and Tsai T.-W., Modeling of exural beams subjected to arbitrary end loads, Journal of Mechanical Design. (2002) 124, 223–235.
10.1115/1.1455031
Web of Science® Google Scholar
5 Brady B. H. G. and Brown E. T., Rock Mechanics for Underground Mining, 1993, 2nd edition, Chapman & Hall, London, UK.
Google Scholar
6 Obert L. and Duvall W. L., Rock Mechanics and the Design of Structures in Rock, 1967, Wiley & Sons, New York, NY, USA.
Google Scholar
7 Popov E. P., Mechanics of Materials, 1978, Prentice Hall International, Englewood Cliffs, NJ, USA.
Google Scholar
8 Jaeger J. C. and Cook N. G. W., Fundamentals of Rock Mechanics, 1969, Methuen, London, UK.
Google Scholar
9 Jaegar J. C., Cook N. G. W., and Zimmerman R. W., Fundamentals of Rock Mechanics, 2007, 4th edition, Blackwell, Oxford, UK.
Google Scholar
10 Segal L. A. and Handelman G. H., Mathematics Applied to Continuum Mechanics, 1977, Macmillan, New York, NY, USA, 0502508, ZBL0371.73006.
Google Scholar
11 van der Merwe J. N. and Madden B. J., Rock Engineering for Underground Coal Mining, 2011, 2nd edition, Southern African Institute of Mining and Metallurgy, Johannesburg, South Africa, Special Publications, Series 8.
Google Scholar
12 van der Merwe J. N. and Madden B. J., Rock Engineering for Underground Coal Mining, 2011, 2nd edition, Southern African Institute of Mining and Metallurgy, Johannesburg, South Africa, 208–218, Special Publications, Series 8.
Google Scholar

Citing Literature

All articles

Controlled Roof Collapse during Secondary Mining in Coal Mines

Abstract

1. Introduction

2. Model

3. Derivation of the Differential Equation

4. Mathematical Solution

5. Analysis of the Results

6. Numerical Estimates

7. Values of the Beam Number B Greater Than B₁

8. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Controlled Roof Collapse during Secondary Mining in Coal Mines

Abstract

1. Introduction

2. Model

3. Derivation of the Differential Equation

4. Mathematical Solution

5. Analysis of the Results

6. Numerical Estimates

7. Values of the Beam Number B Greater Than B1

8. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

7. Values of the Beam Number B Greater Than B₁