Volume 2012, Issue 1 796814

Research Article

Open Access

Exponential Time Integration and Second-Order Difference Scheme for a Generalized Black-Scholes Equation

Zhongdi Cen,

Corresponding Author

Zhongdi Cen

[email protected]

Institute of Mathematics, Zhejiang Wanli University, Zhejiang, Ningbo 315100, China zwu.edu.cn

Search for more papers by this author

Anbo Le,

Anbo Le

Institute of Mathematics, Zhejiang Wanli University, Zhejiang, Ningbo 315100, China zwu.edu.cn

Search for more papers by this author

Aimin Xu,

Aimin Xu

Institute of Mathematics, Zhejiang Wanli University, Zhejiang, Ningbo 315100, China zwu.edu.cn

Search for more papers by this author

Zhongdi Cen,

Corresponding Author

Zhongdi Cen

[email protected]

Institute of Mathematics, Zhejiang Wanli University, Zhejiang, Ningbo 315100, China zwu.edu.cn

Search for more papers by this author

Anbo Le,

Anbo Le

Institute of Mathematics, Zhejiang Wanli University, Zhejiang, Ningbo 315100, China zwu.edu.cn

Search for more papers by this author

Aimin Xu,

Aimin Xu

Institute of Mathematics, Zhejiang Wanli University, Zhejiang, Ningbo 315100, China zwu.edu.cn

Search for more papers by this author

First published: 19 February 2012

https://doi.org/10.1155/2012/796814

Citations: 4

Academic Editor: Kai Diethelm

Share a link

Email
Wechat
Bluesky

Abstract

We apply an exponential time integration scheme combined with a central difference scheme on a piecewise uniform mesh with respect to the spatial variable to evaluate a generalized Black-Scholes equation. We show that the scheme is second-order convergent for both time and spatial variables. It is proved that the scheme is unconditionally stable. Numerical results support the theoretical results.

1. Introduction

The pricing and hedging of derivative securities, also known as contingent claims, is a subject of much practical importance. One basic type of derivative is an option. The owner of a call option has the right but not the obligation to purchase an underlying asset (such as a stock) for a specified price (called the exercise price or strike price) on or before a expiry date. A put option is similar except the owner of such a contract has the right but not the obligation to sell. Options which can be exercised only on the expiry date are called European, whereas options which can be exercised any time up to and including the expiry date are classified as American. It was shown by Black and Scholes [1] that these option prices satisfy a second-order partial differential equation with respect to the time horizon t and the underlying asset price x. This equation is now known as the Black-Scholes equation and can be solved exactly when the coefficients are constant or space-independent. However, in many practical situations, numerical solutions are normally sought. Therefore, efficient and accurate numerical algorithms are essential for solving this problem accurately.

The Black-Scholes differential operator at x = 0 is degenerate. A common and widely used approach by many authors dealing with finite difference/volume/element methods for the Black-Scholes equation is to apply an Euler transformation to remove the degeneracy of the differential operator when the parameters of the Black-Scholes equation are constant or space independent, see for example [2–7]. As a result of the Euler transformation, the transformed interval becomes (−∞, ∞). However, the truncation on the left-hand side of the domain to artificially remove the degeneracy may cause computational errors. Furthermore, the uniform mesh on the transformed interval will lead to the originally grid points concentrating around x = 0 inappropriately. Moreover, when a problem is space-dependent, this transformation is impossible, and thus the Black-Scholes equation in the original form needs to be solved.

It is well known that when using the standard finite difference method to solve those problems involving the convection-diffusion operator, such as the Black-Scholes differential operator, numerical difficulty can be caused. The main reason is that when the volatility or the asset price is small, the Black-Scholes differential operator becomes a convection-dominated operator. Hence, the implicit Euler scheme with central spatial difference method may lead to nonphysical oscillations in the computed solution. The implicit Euler scheme with upwind spatial difference method does not have this disadvantage, but this difference scheme is only first-order convergent [8]. Recently, a stable fitted finite volume method [9] is employed for the discretization of the Black-Scholes equation. But it is also first-order convergent. In [10, 11] numerical methods of option pricing models are studied by applying a standard finite volume method to obtain a difference scheme. Their numerical schemes use central difference for a given mesh, but switch to upstream weighting for a small number of nodes, which are second-order spatial convergent. In this paper we change the grid spacing to a piecewise uniform mesh which is constructed so that central difference is used everywhere.

For time discretization, explicit schemes are easy to implement but suffer from stability problems. Some well-known second-order implicit schemes, such as Crank-Nicolson method, are prone to spurious oscillations unless the time step size is no more than twice the maximum time step size for an explicit method (see Zvan et al. [10, 11]). Although the fully implicit backward Euler method may be used to accurately solve the Black-Scholes PDE due to its strong stability properties, it is only first-order accurate in time. Exponential time integration has gained importance following the work of Cox and Matthews [12] and with recent developments in efficient methods for computing the matrix exponential [13–16], this time evolution method is likely to be a popular choice for solving large semidiscrete systems arising in various numerical computations.

In [17, 18], we have presented robust difference schemes for the Black-Scholes equation, which is based on the implicit Euler method for time discretization and a central difference method for spatial discretization. In this paper, we apply an exponential time integration scheme combined with a central difference scheme on a piecewise uniform mesh with respect to the spatial variable. We show that our scheme is second-order convergent for both time and spatial variables, while in [17, 18] the convergence for the time variable is only first order. It is proved that the scheme is unconditionally stable. Numerical results support this conclusion.

The rest of the paper is organized as follows. In the next section we discuss the continuous model of the Black-Scholes equations. The discretization method is described in Section 3. It is shown that the finite difference scheme is second-order convergent with respect to both spatial and time variables. In Section 4 we prove that the difference scheme is unconditionally stable. Finally numerical examples are presented in Section 5.

2. The Continuous Problem

We consider the following generalized Black-Scholes equation

()

Here v(x, t) is the European call option price at asset price x and at time to maturity t, K is the exercise price, T is the maturity, r(t) is the risk-free interest rate, and σ(x, t) represents the volatility function of underlying asset. Here we assume that σ² ≥ α > 0, β^* ≥ r ≥ β > 0. When σ and r are constant functions, it becomes the classical Black-Scholes model.

Even though as x goes to zero the generalized Black-Scholes operator (2.1) is degenerate, the existence and uniqueness of a solution of (2.1)–(2.3) is well known. Due to the fact that the initial condition is not smooth, the finite difference scheme may not converge to the exact solution.

We first modify the model as follows. Define π_ε(y) as

()

where 0 < ε ≪ 1 is a transition parameter and π_ɛ(y) is a function which smooths out the original max (y, 0) around y = 0. This requires that π_ɛ(y) satisfies

()

Using these ten conditions we can easily find that

()

Replacing max (x − K, 0) in the initial condition (2.2) by the fourth-order smooth function π_ε(x − K) we obtain

()

The existence and uniqueness of a solution of (2.7)–(2.9) can be found in [19], which also gives the following result: for (x, t)∈[0, +∞)×[0, T],

()

where C is a positive constant.

In order to apply the numerical method we need to truncate the infinite domain [0, +∞)×[0, T] into Ω = [0, S_max]×[0, T], where S_max is suitably chosen positive number. Based on Wilmott et al.’s estimate [20] that the upper bound of the asset price S_max is typically three or four times the strike price, it is reasonable for us to set S_max = 4K. Thus we consider the following problem:

()

The existence and uniqueness of a solution of (2.11)–(2.14) can be also found in [19], which also gives the following result:

()

It follows from (2.10) and (2.15) that we can make the solution of our modified model (2.11)–(2.14) close to that of the original model (2.1)–(2.3) by choosing sufficiently small ɛ and sufficiently large S_max. In the remaining of this paper we will consider the model (2.11)–(2.14).

3. Discretization Scheme

The exponential time differencing scheme is an approach used for the numerical solution of a wide range of PDEs that involve spatial variables as well as a time variable. The spatial discretization results in an approximating system of ODEs. For an inhomogeneous linear PDE, this method leads to an inhomogeneous linear system of ODEs in time whose solution satisfies a two-term recurrence relation involving the matrix exponential, where the matrix is determined by the form of spatial discretization applied such as finite difference, finite element, or spectral approach. In this paper we use a central difference scheme on a piecewise uniform mesh for approximating the spatial derivatives.

The use of central difference scheme on the uniform mesh may produces nonphysical oscillations in the computed solution. To overcome this oscillation we use a piecewise uniform mesh Ω^N+1 on the space interval [0, S_max]:

()

where

()

Here we have used a refined mesh at the region near x = K for treating the nonsmoothness of the payoff function. It is easy to see that the mesh sizes h_i = x_i − x_i−1 satisfy

()

We discretize the generalized Black-Scholes operator using a central difference scheme on the above piecewise uniform mesh:

()

for i = 1, …, N − 1. This discretization leads to an initial value problem of the form

()

where U(t) = (U₁(t), …, U_N−1(t)) ^T, the matrix A(t) of order (N − 1) is given by

()

with

()

The vectors f(t) and π_ε(x − K) are the corresponding boundary and initial conditions:

()

Lemma 3.1. For each t the matrix A(t) is strictly diagonally dominant.

Proof. It is easy to see that

()

for sufficiently large N. Clearly,

()

Hence we verify that the matrix A(t) is strictly diagonally dominant.

Solving the system of (3.5) gives

()

which satisfies the following recurrence relation:

()

in which l is a constant time step in the discretization of the time variable t ≥ 0, at the points t_j = jl (j = 0,1, 2, …, M).

Using a numerical integration rule for evaluating the quadrature in (3.12) gives the following second-order formula:

()

Now the problem is how to approximate e^lA(t) to get numerical solution. A good approximation to e^z is the (b, d) Padé approximation which has the form [21, 22]

()

where P_d(z) and Q_b(z) are the polynomials of degrees d and b, respectively, with real coefficients, in each of which the constant term is unity.

The numerical method to be employed here is based on the use of the following second-order rational approximation:

()

So we have

()

for the matrix exponentials in our recurrence relation (3.13).

Using (3.13) and (3.16) we get

()

for t = 0, l, 2l, …, M, where

()

It can be seen that the truncation error of the difference scheme (3.17) with is O(h² + l²) (see [21], e.g.).

4. Stability Analysis

Lemma 4.1. For each t the real part of each nonzero eigenvalue of A(t) is negative.

Proof. From Lemma 3.1 we can obtain that for each t the matrix −A(t) is an M-matrix, thus the real part of each nonzero eigenvalue of −A(t) is positive (see [23, Theorem 3.1]). Hence the real part of each nonzero eigenvalue of A(t) is negative.

Theorem 4.2. The difference scheme (3.17) is unconditionally stable.

Proof. Let λ_i (i = 1,2, …, N − 1) be eigenvalues of matrix A(t) for a fixed t, then

()

are eigenvalues of matrix

()

Let

is the conjugate complex of λ_i. It is easy to check

()

where we have used Lemma 4.1. Hence we have

()

From this we complete the proof.

5. Numerical Experiments

In this section we verify experimentally the theoretical results obtained in the preceding section. Errors and convergence rates for the numerical scheme are presented for two test problems.

Test 1 European call option with parameters: σ = 0.2 + 0.2(1 − t)((x/25 − 1.2) ²/((x/25) ² + 1.44))) , r = 0.06, T = 1, K = 25 and S_max = 100.

Test 2 European call option with parameters: σ = 0.2[1 + 0.1(1 − t)(x/(1 + x))], r = 0.06, T = 1, K = 25 and S_max = 100.

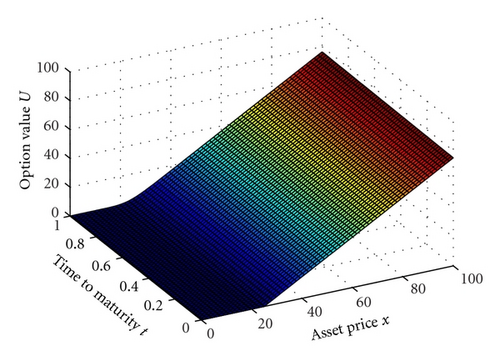
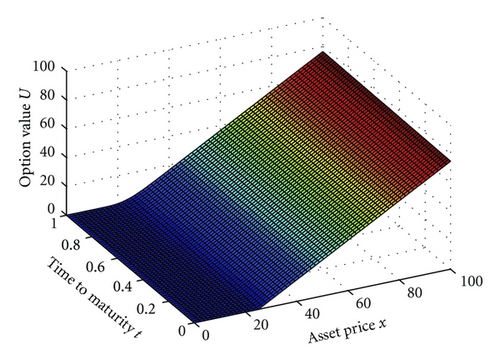
For Tests 1 and 2 we choose of the rational approximation (3.17). The computed option value U with N = M = 64 are depicted in Figures 1 and 2, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Computed option value U for Test 1.

The exact solutions of our test problems are not available. We use the approximated solution obtained by the implicit Euler method in [17] with N = 2048, M = 2048 as the exact solution since we know this method converges. Because we only know "the exact solution" on mesh points, we use the linear interpolation to get solutions at other points. In this paper

denotes “the exact solution” which is a linear interpolation of the approximated solution U^2048,2048 obtained by the implicit Euler method. We measure the accuracy in the discrete maximum norm

()

and the convergence rate

()

for the exponential time integration method and the implicit Euler method in [17]. The error estimates and convergence rates in our computed solutions of Tests 1 and 2 from both methods are listed in Tables 1 and 2, respectively.

Table 1. Numerical results for Test 1.

M	N	Exponential method		Implicit Euler method
M	N	Error e^N,M	Rate r^N,M	Error e^N,M	Rate r^N,M
16	64	1.2535e − 1	—	1.7817e − 1	—
32	128	2.9268e − 2	2.099	8.9567e − 2	0.992
64	256	1.5725e − 2	0.896	4.6822e − 2	0.936

Table 2. Numerical results for Test 2.

M	N	Exponential method		Implicit Euler method
M	N	Error e^N,M	Rate r^N,M	Error e^N,M	Rate r^N,M
16	64	1.0716e − 1	—	1.7428e − 1	—
32	128	2.4716e − 2	2.116	8.9504e − 2	0.961
64	256	1.5810e − 2	0.645	4.7780e − 2	0.906

From the figures it is seen that the numerical solutions by our method are nonoscillatory. We compare the accuracy of the exponential time integration method with the implicit Euler method in [17]. From Tables 1 and 2 we can see the exponential time integration method converges more rapidly than the implicit Euler method in [17], but for the same M and N the exponential time integration method require more computer time than the implicit Euler method. We also can see that r^N,M of the exponential time integration method is close to 2, even though this rate is not reached for large M and N, the reason is that the “exact solution” is not really the exact solution. Therefore the numerical results support the convergence estimate of Theorem 4.2.

Acknowledgments

The authors would like to thank the anonymous referee for several suggestions for the improvement of this paper. The work was supported by Zhejiang Province Natural Science Foundation (Grant nos. Y6100021, Y6110310) of China and Ningbo Municipal Natural Science Foundation (Grant no. 2010A610099) of China.

References

1 Black F. and Scholes M. S., The pricing of options and corporate liabilities, Journal of Political Economy. (1973) 81, 637–654.
10.1086/260062
Web of Science® Google Scholar
2 Courtadon G., A more accurate finite difference approximation for the valuation of options, Journal of Financial and Quantitative Analysis. (1982) 17, 697–703.
10.2307/2330857
Web of Science® Google Scholar
3 Giles M. and Carter R., Convergence analysis of Crank-Nicolson and Rannacher time-marching, Journal of Computational Finance. (2006) 94, 89–112.
10.21314/JCF.2006.152
Google Scholar
4 Pooley D. M., Vetzal K. R., and Forsyth P. A., Convergence remedies for non-smooth payoffs in option pricing, Journal of Computational Finance. (2003) 6, no. 4, 25–40.
10.21314/JCF.2003.101
Google Scholar
5 Schwartz E., The valuation of warrants: implementing a new approach, The Journal of Financial Economics. (1977) 13, 79–93.
10.1016/0304-405X(77)90037-X
Web of Science® Google Scholar
6 Tangman D. Y., Gopaul A., and Bhuruth M., Numerical pricing of options using high-order compact finite difference schemes, Journal of Computational and Applied Mathematics. (2008) 218, no. 2, 270–280, 2427213, https://doi.org/10.1016/j.cam.2007.01.035, ZBL1146.91338.
10.1016/j.cam.2007.01.035
Web of Science® Google Scholar
7 Zhao J., Davison M., and Corless R. M., Compact finite difference method for American option pricing, Journal of Computational and Applied Mathematics. (2007) 206, no. 1, 306–321, 2337446, https://doi.org/10.1016/j.cam.2006.07.006, ZBL1151.91552.
10.1016/j.cam.2006.07.006
Web of Science® Google Scholar
8 Vázquez C., An upwind numerical approach for an American and European option pricing model, Applied Mathematics and Computation. (1998) 97, no. 2-3, 273–286, https://doi.org/10.1016/S0096%2D3003(97)10122%2D9, 1643127.
10.1016/S0096-3003(97)10122-9
Web of Science® Google Scholar
9 Wang S., A novel fitted finite volume method for the Black-Scholes equation governing option pricing, IMA Journal of Numerical Analysis. (2004) 24, no. 4, 699–720, 2094577, https://doi.org/10.1093/imanum/24.4.699, ZBL1147.91332.
10.1093/imanum/24.4.699
Web of Science® Google Scholar
10 Zvan R., Forsyth P., and Vetzal K., Robust numerical methods for PDE models of Asian options, The Journal of Financial Economics. (1998) 1, no. 2, 39–78.
Google Scholar
11 Zvan R., Forsyth P. A., and Vetzal K. R., A finite volume approach for contingent claims valuation, IMA Journal of Numerical Analysis. (2001) 21, no. 3, 703–731, 1844364, https://doi.org/10.1093/imanum/21.3.703, ZBL1004.91032.
10.1093/imanum/21.3.703
Web of Science® Google Scholar
12 Cox S. M. and Matthews P. C., Exponential time differencing for stiff systems, Journal of Computational Physics. (2002) 176, no. 2, 430–455, 1894772, https://doi.org/10.1006/jcph.2002.6995, ZBL1005.65069.
10.1006/jcph.2002.6995
CAS Web of Science® Google Scholar
13 Rambeerich N., Tangman D. Y., Gopaul A., and Bhuruth M., Exponential time integration for fast finite element solutions of some financial engineering problems, Journal of Computational and Applied Mathematics. (2009) 224, no. 2, 668–678, 2492899, https://doi.org/10.1016/j.cam.2008.05.047, ZBL1154.91472.
10.1016/j.cam.2008.05.047
Web of Science® Google Scholar
14 Tangman D. Y., Gopaul A., and Bhuruth M., Exponential time integration and Chebychev discretisation schemes for fast pricing of options, Applied Numerical Mathematics. (2008) 58, no. 9, 1309–1319, https://doi.org/10.1016/j.apnum.2007.07.005, 2444259, ZBL1151.91546.
10.1016/j.apnum.2007.07.005
Web of Science® Google Scholar
15 Tian Z. F. and Yu P. X., A high-order exponential scheme for solving 1D unsteady convection-diffusion equations, Journal of Computational and Applied Mathematics. (2011) 235, no. 8, 2477–2491, 2763161, https://doi.org/10.1016/j.cam.2010.11.001, ZBL1209.65090.
10.1016/j.cam.2010.11.001
Web of Science® Google Scholar
16 Yousuf M., Efficient L-stable method for parabolic problems with application to pricing American options under stochastic volatility, Applied Mathematics and Computation. (2009) 213, no. 1, 121–136, 2533368, https://doi.org/10.1016/j.amc.2009.02.060.
10.1016/j.amc.2009.02.060
Web of Science® Google Scholar
17 Cen Z. and Le A., A robust and accurate finite difference method for a generalized Black-Scholes equation, Journal of Computational and Applied Mathematics. (2011) 235, no. 13, 3728–2733, https://doi.org/10.1016/j.cam.2011.01.018, 2794165, ZBL1214.91130.
10.1016/j.cam.2011.01.018
Web of Science® Google Scholar
18 Cen Z., Le A., and Xu A., A second-order difference scheme for the penalized Black-Scholes equation governing American put option pricing, Computational Economics. In presshttps://doi.org/10.1007/s10614%2D011%2D9268%2D9.
10.1007/s10614-011-9268-9
Google Scholar
19 Cho C.-K., Kim T., and Kwon Y., Estimation of local volatilities in a generalized Black-Scholes model, Applied Mathematics and Computation. (2005) 162, no. 3, 1135–1149, 2113958, https://doi.org/10.1016/j.amc.2004.02.001, ZBL1079.91022.
10.1016/j.amc.2004.02.001
Web of Science® Google Scholar
20 Wilmott P., Dewynne J., and Howison S., Option Pricing: Mathematical Models and Computation, 1993, Oxford Financial Press, Oxford, UK.
Web of Science® Google Scholar
21 Dehghan M., Numerical techniques for a parabolic equation subject to an overspecified boundary condition, Applied Mathematics and Computation. (2002) 132, no. 2-3, 299–313, 1920486, https://doi.org/10.1016/S0096%2D3003(01)00194%2D1, ZBL1024.65088.
10.1016/S0096-3003(01)00194-1
Web of Science® Google Scholar
22 Smith G. D., Numerical Solution of Partial Differential Equations (Finite Difference Method), 1985, 3rd edition, The Clarendon Press Oxford University Press, New York, NY, USA, 827497.
Google Scholar
23 Poole G. and Boullion T., A survey on M-matrices, SIAM Review. (1974) 16, 419–427, 0352146, https://doi.org/10.1137/1016079.
10.1137/1016079
Web of Science® Google Scholar

Citing Literature

All articles

Exponential Time Integration and Second-Order Difference Scheme for a Generalized Black-Scholes Equation

Abstract

1. Introduction

2. The Continuous Problem

3. Discretization Scheme

4. Stability Analysis

5. Numerical Experiments

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exponential Time Integration and Second-Order Difference Scheme for a Generalized Black-Scholes Equation

Abstract

1. Introduction

2. The Continuous Problem

3. Discretization Scheme

4. Stability Analysis

5. Numerical Experiments

Acknowledgments

References

Citing Literature

Figures

References

Related

Information