Unsteady Stagnation Point Flow and Heat Transfer over a Stretching/Shrinking Sheet with Suction or Injection
Abstract
The unsteady stagnation point flow and heat transfer over a stretching/shrinking sheet with suction/injection is studied. The governing partial differential equations are converted into nonlinear ordinary differential equations using a similarity transformation and solved numerically. Both stretching and shrinking cases are considered. Results for the skin friction coefficient, local Nusselt number, velocity, and temperature profiles are presented for different values of the governing parameters. It is found that the dual solutions exist for the shrinking case, whereas the solution is unique for the stretching case. Numerical results show that the range of dual solutions increases with mass suction and decreases with mass injection.
1. Introduction
The study of flow and heat transfer over a stretching/shrinking sheet receives considerable attention from many researchers due to its variety of application in industries such as extrusion of a polymer in a melt spinning process, manufacturing plastic films, wire drawing, hot rolling, and glass fiber production. Sakiadis [1, 2] reported the flow field analysis where the stretched surface was assumed to move with uniform velocity, and similarity solutions were obtained for the governing equations. Crane [3] gave a closed-form solution for steady two-dimensional flow of an incompressible viscous fluid caused by the stretching of an elastic sheet, which moves in its own plane with a velocity which varies linearly with distance from a fixed point. Chiam [4] investigated the steady two-dimensional stagnation point flow towards a stretching surface in the case when the stretching velocity is identical to the free stream velocity. P.S. Gupta and A.S. Gupta [5] extended the work of Crane [3] by investigating the effect of mass transfer on a stretching sheet with suction or blowing for linear surface velocity subject to uniform temperature. Mahapatra and Gupta [6] investigated the steady two-dimensional magnetohydrodynamics (MHDs) stagnation point flow of an incompressible viscous electrically conducting fluid toward a stretching surface, the flow being permeated by a uniform transverse magnetic field. In studying similar problem to Chiam [4], Mahapatra and Gupta [7] observed that the structure of the boundary layer depends on the stretching sheet parameters and the angle of incidence. Mahapatra and Gupta [8] obtained the exact similarity solution of the Navier-Stokes equations by considering the combination of both stagnation flow and stretching surface and observed that the flow displays a boundary-layer structure when the stretching velocity of the surface is less than the free stream velocity. Lok et al. [9] extended the Mahapatra and Gupta’s work [8] to the oblique stagnation flow and found that the free stream obliqueness is the shift of the stagnation point toward the incoming flow and depends on the inclination angle. Miklavcic and Wang [10] obtained the solution for steady two-dimensional, as well as axisymmetric viscous, flow over a shrinking sheet. Fang and Zhang [11] obtained the closed-form solution for steady MHD flow over a shrinking surface subject to applied suction. Wang [12] investigated the steady two-dimensional and axisymmetric stagnation point flow with heat transfer over a shrinking sheet and found that solutions do not exist for the larger shrinking rates. Ishak et al. [13] extended the work of Mahapatra and Gupta [8] to the oblique stagnation flow and a shrinking sheet in a micropolar fluid. It was found in these problems that the solutions for a shrinking sheet are non-unique. Bachok et al. [14] considered the similarity solutions of stagnation point flow and heat transfer over a warm, laminar liquid flow to a melting stretching or shrinking sheet. Recently, Patel and Timol [15] analyzed the steady two-dimensional stagnation point flow and heat transfer of a non-Newtonian fluid. In the unsteady flow problem, Wang [16] studied the concept of the flow and investigated the behavior of liquid film on an unsteady stretching surface. Andersson et al. [17] presented a new similarity solution for the temperature field on an unsteady stretching surface by transforming the time-dependent thermal energy equation into an ordinary differential equation. Elbashbeshy and Bazid [18] presented an exact similarity solution for unsteady flow and heat transfer over a horizontal stretching surface and studied the effect of various governing parameters such as the Prandtl number and unsteadiness parameter which determine the velocity and temperature profiles and heat transfer coefficient. Later, Fang [19] extended the flow over a shrinking sheet to power law surface velocity and obtained the multiple solutions for certain mass transfer with controlling parameters. Tsai et al. [20] studied numerically the nonuniform heat source or sink effect on the flow and heat transfer from an unsteady stretching sheet through a quiescent fluid. The results showed that the heat transfer rate and the skin friction increase as the unsteadiness parameter increases, but, as the space- and temperature-dependent parameters for heat source/sink increase, the heat transfer rate and the skin friction decrease. Sajid and Hayat [21] investigated the effect of the MHD for two-dimensional and axisymmetric shrinking sheet. Later, Fang et al. [22] found that multiple solutions exist for a certain range of mass suction and unsteadiness parameters for the unsteady viscous flow over a continuously shrinking sheet. Recently, Adhikary and Misra [23] investigated the unsteady two-dimensional hydromagnetic flow and heat transfer of an incompressible viscous fluid. Ali et al. [24] presented the influence of rotation, unsteadiness, and mass suction parameters on the reduced skin friction coefficients as well as the lateral velocity and velocity profiles for the unsteady viscous flow over a shrinking sheet with mass transfer in a rotating fluid. Recently, Fang et al. [25] investigated the boundary layers of an unsteady incompressible stagnation point flow with mass transfer whereas Bhattacharyya [26] found that the dual solutions for velocity distribution exist for certain value of velocity ratio parameter for the dual solutions in unsteady stagnation point flow over a shrinking sheet. Very recently, Nik Long et al. [27] found that multiple solutions exist for a certain range of ratio of the shrinking velocity to the free stream velocity which again depends on the unsteadiness parameter for the unsteady stagnation point flow and heat transfer over a stretching/shrinking sheet. The aim of this work is to extend the paper by Nik Long et al. [27] to the case of unsteady stagnation point flow of an incompressible viscous fluid by considering both stretching and shrinking sheets with suction or injection. The momentum and heat equation are solved numerically, and the characteristics of the flow are obtained.
2. Mathematical Formulation
3. Results and Discussion
The nonlinear ordinary differential equations (2.7) subject to the boundary conditions (2.8) are solved numerically using the shooting method where we convert the boundary value problem into an initial value problem. The numerical results are given to carry out a parametric study showing the influence of the nondimensional parameters: the unsteadiness parameters A, ε, Prandtl number Pr, and f0. For the validation of numerical results, the case A = 0 and Pr = 0.7 with no effect of suction or injection (f0 = 0) are considered and compared to those of Wang [12]. The quantitative comparison is shown in Table 1 for the variation of ε with parameter f0 and found to be in favorable agreement. Based on our computations, the critical values of ε, εc with parameter f0 are presented in Table 2 and compare well with the previous results reported by Nik Long et al. [27]. It is observed that the values of |εc| increase as f0 increases. Hence, suction delays the boundary layer separation, whereas injection accelerates it.
| A | ε | Wang [12] | Present | ||
|---|---|---|---|---|---|
| First solution | Second solution | First solution | Second solution | ||
| 0 | 3 | −4.276545 | |||
| 0.2 | 1.05113 | 1.051130 | |||
| 0.1 | 1.14656 | 1.146561 | |||
| −0.1 | 1.30860 | 1.308602 | |||
| −0.25 | 1.40224 | 1.402240 | |||
| −0.5 | 1.49567 | 1.495672 | |||
| −1.0 | 1.32882 | 0 | 1.328817 | 0 | |
| −1.15 | 1.08223 | 0.116702 | 1.082232 | 0.116702 | |
| A | f0 | Nik Long et al. [27] | Present |
|---|---|---|---|
| −0.3 | −0.265432 | ||
| −2 | 0 | −0.439398 | |
| 0.3 | −0.638668 | ||
| −0.3 | −0.816678 | ||
| −0.5 | 0 | −0.956566 | |
| 0.3 | −1.139657 | ||
| 0.01 | 0 | −1.2536 | −1.253600 |
| −0.3 | −1.464110 | ||
| 0.5 | 0 | −1.601111 | |
| 0.3 | −1.725011 | ||
| −0.3 | −1.969922 | ||
| 2 | 0 | −2.138974 | |
| 0.3 | −2.383360 | ||
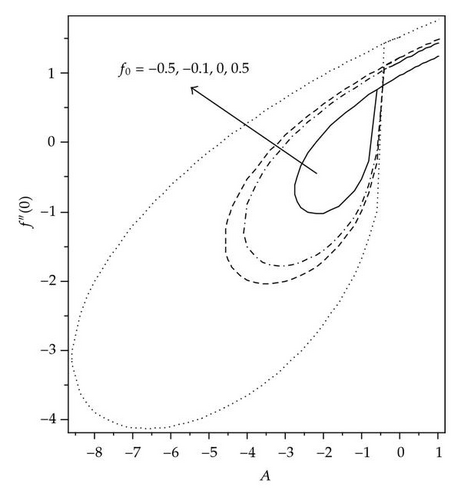
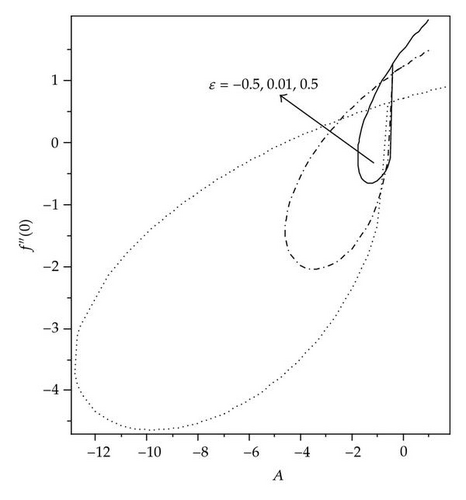
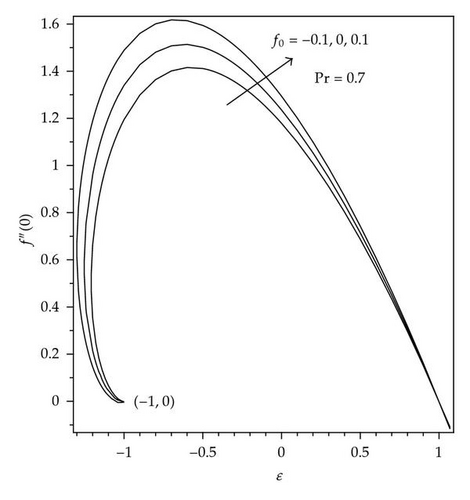
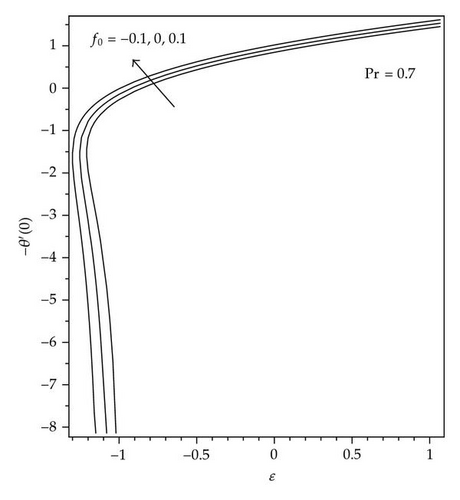
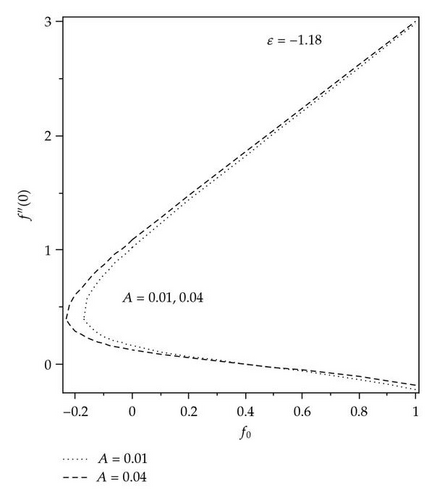
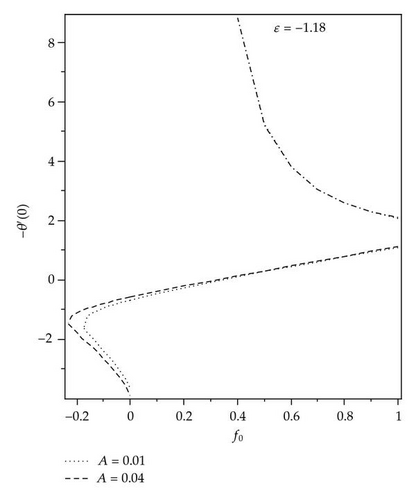
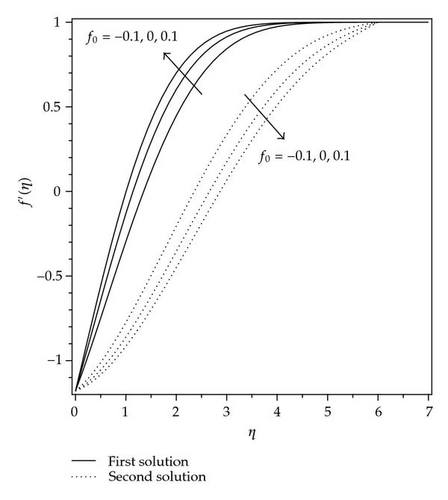
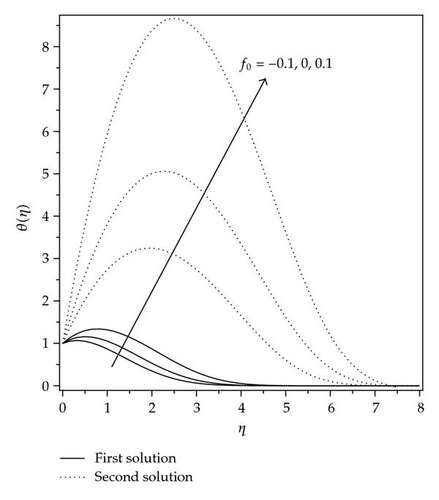
The solution domains for f′′(0) are shown in Figures 1 and 2 for different mass transfer parameters f0 and ε, respectively. It is seen that there exist dual solutions for Ac < A < 0 where Ac is a critical number dependent on f0. The solution is unique for (A > 0)∪(A = Ac), and there is no solution for (A < Ac). The existence of the dual solution in our case is in agreement with [25, 28, 29]. The effect of ε and the mass suction (f0 > 0) enlarge the solution domain, and the mass injection (f0 < 0) reduces it. The velocity gradient decreases with decreasing values of A for the first and second solutions from positive to negative values of f′′(0), which indicates that there exist multiple regions for the momentum boundary layer. Figures 3 and 4 show the relationship between the skin friction coefficient and the local Nusselt number with ε and for the various values of f0. It is observed that there is no solutions for ε < εc, the dual solutions exist for εc < ε ≤ −1.0, and the solutions are unique for ε > −1.0, which means that the boundary layer separates from the surface. Figures 5 and 6 show the skin friction coefficient and the local Nusselt number with f0, respectively, for ε = −1.18 and A = 0.01,0.04. For these values of ε, critical value (f0,c) of f0 being negative at which, there is a saddle node bifurcation. The dual solutions exist beyond the critical number which is f0 > f0,c, but there is no solution for f0 < f0,c. This behavior of solution indicates that the solutions exist for a certain interval of ε the case of injection, whereas no such interval appears for the suction, with both branches of solutions continuing to large value of f0. The skin friction coefficient f′′(0) and the local Nusselt number –θ′(0) increase as the parameter A increases and decrease as f0 increases. The samples of velocity and temperature profiles are presented in Figures 7 and 8, respectively, for different values of f0, ε = −1.18, and A = 0.01. These figures show that the boundary conditions (2.8) for (2.7) are satisfied and approached infinity asymptotically, which support the numerical results presented in Figures 3, 4, 5, and 6 and exhibit the existence of the dual solution. We observed that the temperature profiles increase as the values of f0 increase. The same behavior of solution is observed for the velocity profiles.
4. Conclusion
A numerical study is performed for the problem of unsteady two-dimensional stagnation point flow and heat transfer over a stretching and shrinking sheets with suction or injection. The similarity transformation is used to reduce the partial differential equations into nonlinear ordinary differential equations. The effects of the mass suction or mass injection parameters f0, governing parameters A, and ε on the fluid flow and heat transfer characteristics have been discussed, and the numerical results obtained are comparable well with the previously reported cases. It was found that the suction (f0 > 0) widens the range of ε for which solution exists, whereas the injection (f0 < 0) acts in the opposite manner. Moreover, for the shrinking sheet, the dual solutions exist whereas for the stretching sheet the solution is found to be unique for all ε.
Acknowledgment
The second author would like to thank the Ministry of Higher Education (MOHE) for the Grant no. 03-11-08-670FR.




