Journal of Applied Mathematics
Volume 2012, Issue 1 764894
Research Article
Open Access

Numerical Studies for Fractional-Order Logistic Differential Equation with Two Different Delays

N. H. Sweilam, 

Corresponding Author

N. H. Sweilam

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author
M. M. Khader, 

M. M. Khader

Department of Mathematics, Faculty of Science, Benha University, Benha 15318, Egypt bu.edu.eg

Search for more papers by this author
A. M. S. Mahdy, 

A. M. S. Mahdy

Department of Mathematics, Faculty of Science, Zagazig University, Zagazig 44519, Egypt zu.edu.eg

Search for more papers by this author
First published: 19 September 2012
https://doi.org/10.1155/2012/764894
Citations: 41
Academic Editor: J. Biazar

Abstract

A numerical method for solving the fractional-order logistic differential equation with two different delays (FOLE) is considered. The fractional derivative is described in the Caputo sense. The proposed method is based upon Chebyshev approximations. The properties of Chebyshev polynomials are utilized to reduce FOLE to a system of algebraic equations. Special attention is given to study the convergence and the error estimate of the presented method. Numerical illustrations are presented to demonstrate utility of the proposed method. Chaotic behavior is observed and the smallest fractional order for the chaotic behavior is obtained. Also, FOLE is studied using variational iteration method (VIM) and the fractional complex transform is introduced to convert fractional Logistic equation to its differential partner, so that its variational iteration algorithm can be simply constructed. Numerical experiment is presented to illustrate the validity and the great potential of both proposed techniques.

1. Introduction

It is known that delay differential equation (DDE) provides a mathematical model for many systems in different fields such as physical, biological systems in which the rate of change of the system depends upon their past history [1, 2]. Introduction of delay in the model enriches its dynamics and allows a precise description of the real life phenomena. DDEs are proved useful in control systems [3], lasers, traffic models [4], metal cutting, epidemiology, neuroscience, population dynamics [2], chemical kinetics [1], and so forth. In DDE one has to provide history of the system over the delay interval [−τ; 0] as the initial condition. Due to this reason delay systems are infinite dimensional in nature. Because of infinite dimensionality the DDEs are difficult to analyse analytically [5] and hence the numerical solutions play an important role.

On the other side, ordinary and partial fractional differential equations have been the focus of many studies due to their frequent appearance in various applications in fluid mechanics, viscoelasticity, biology, physics and engineering [6]. Consequently, considerable attention has been given to the solutions of fractional differential equations of physical interest. Most fractional differential equations do not have exact solutions, so approximate and numerical techniques [7–12], must be used. Recently, several numerical methods to solve the fractional differential equations have been given such as variational iteration method [13–19], homotopy perturbation method [20], Adomian′s decomposition method [21], homotopy analysis method [22], fractional complex transform [15, 23, 24], and collocation method [25–31].

Let us describe some necessary definitions and mathematical preliminaries of the fractional calculus theory required for our subsequent development.

Definition 1.1. The Caputo fractional derivative operator Dα of order α is defined in the following form:

()
where m − 1 < α ≤ m,   m ∈ ℕ,   x > 0.

Similar to integer-order differentiation, Caputo fractional derivative operator is a linear operation:

()
where λ and μ are constants. For the Caputo′s derivative we have [32]:
()
We use the ceiling function ⌈α⌉ to denote the smallest integer greater than or equal to α, and ℕ0 = {0,1, 2, …}. Recall that for α ∈ ℕ, the Caputo differential operator coincides with the usual differential operator of integer order.

For more details on fractional derivatives definitions and its properties see [32–34].

In this paper, we consider FOLE with two delays of the form:

()
the parameter α refers to the fractional order of time derivative with 0 < α ≤ 1.

We also assume an initial condition:

()
This work is motivated by work done by El-Sayed et al. [8]. The stability of the solution, the existence and the uniqueness of the proposed problem (1.4) are introduced in details in [8].

The main idea of the present work is to apply the Chebyshev collocation method to discretize (1.4) to get a system of algebraic equations thus greatly simplifying the problem. Chebyshev polynomials are a well-known family of orthogonal polynomials on the interval [−1,1] that have many applications [28, 35]. They are widely used because of their good properties in the approximation of functions. However, with our best knowledge, very little work was done to adapt these polynomials to the solution of fractional differential equations.

Khader [25] introduced a new approximate formula of the fractional derivation Dαx(t) and used it to solve numerically the fractional diffusion equation. In this paper, we will extend this formula to solve the fractional-order logistic equation with two delays (1.4) and prove the error estimate of the introduced formula.

The organization of this paper is as follows. In the next section, the approximation of fractional derivative Dαx(t) is obtained. Section 3 summarizes the application of Chebyshev collocation method to solve (1.4). In Section 4, the procedure of solution using VIM is given. In Section 5, the use of fractional complex transform is introduced with respect to VIM. Also a conclusion is given in Section 6.

2. Derivation an Approximate Formula for Fractional Derivatives Using Chebyshev Series Expansion

The well-known Chebyshev polynomials [35] are defined on the interval [−1,1] and can be determined with the aid of the following recurrence formula:
()
The analytic form of the Chebyshev polynomials Tn(z) of degree n is given by the following:
()
where [n/2] denotes the integer part of n/2. The orthogonality condition is
()
In order to use these polynomials on the interval [0, L] we define the so called shifted Chebyshev polynomials by introducing the change of variable z = (2/L)t − 1. The shifted Chebyshev polynomials are defined as .
The analytic form of the shifted Chebyshev polynomial of degree n is given by the following:
()
The function x(t), which belongs to the space of square integrable in [0, L], may be expressed in terms of shifted Chebyshev polynomials as follows:
()
where the coefficients ci are given by the following:
()
In practice, only the first (m + 1)-terms shifted Chebyshev polynomials are considered. Then we have the following:
()

Theorem 2.1 (Chebyshev truncation theorem). The error in approximating x(t) by the sum of its first m terms is bounded by the sum of the absolute values of all the neglected coefficients. If the following:

()
then
()
for all x(t), all m, and all t ∈ [−1,1].

Proof. The Chebyshev polynomials are bounded by one, that is, |Tk(t)| ≤ 1 for all t ∈ [−1,1] and for all k. This implies that the k-th term is bounded by |ck|. Subtracting the truncated series from the infinite series, bounding each term in the difference, and summing the bounds gives the theorem.

The main approximate formula of the fractional derivative of x(t) is given in the following theorem.

Theorem 2.2. Let x(t) be approximated by Chebyshev polynomials as (2.7) and also suppose α > 0, then:

()
where is given by the following:
()

Proof. Since the Caputo′s fractional differentiation is a linear operation we have

()
Employing (1.3), in formula (2.4) we have
()
Also, for i = ⌈α⌉, …, m, and by using (1.3), in formula (2.4) we get
()
A combination of (2.13), (2.14), and (2.11) leads to the desired result.

Test example Consider the function x(t) = t2 with m = 3 and α = 1.5, the shifted Chebyshev series of t2 is

()
Now, by using (2.10), we obtain
()
where,
()
therefore,
()

Theorem 2.3. The Caputo fractional derivative of order α for the shifted Chebyshev polynomials can be expressed in terms of the shifted Chebyshev polynomials themselves in the following form:

()
where
()

Proof. We concern the properties of the shifted Chebyshev polynomials [35] and expand tk−α  in (2.14) in the following form [36]:

()
where ckj can be obtained using (2.6), where x(t) = tk−α then,
()
At   j = 0 we find, , also, at any j and using the formulae (2.4) and (2.6) we can find that
()
employing (2.14) and (2.21) gives
()
where
()
After some lengthly manipulation Θi,j,k can put in the following form:
()
and this completes the proof of the theorem.

Theorem 2.4. The error |ET(m)| = |Dαx(t) − Dαxm(t)| in approximating Dαx(t) by Dαxm(t) is bounded by the following:

()

Proof. A combination of (2.5), (2.7), and (2.19) leads to the following:

()
but , so, we can obtain
()
and subtracting the truncated series from the infinite series, bounding each term in the difference, and summing the bounds completes the proof of the theorem.

3. Procedure of Solution for the Fractional-Order Logistic Equation

Consider the FOLE of type given in (1.4). In order to use the Chebyshev collocation method, we first approximate x(t) as follows:
()
From (1.4), (3.1), and Theorem 2.2 we have
()
We now collocate (3.2) at (m + 1 − ⌈α⌉) points tp as follows:
()
For suitable collocation points we use roots of shifted Chebyshev polynomial . Also, by substituting (2.7) in the initial condition (1.5) we can find the following equation:
()
Equation (3.3), together with the equation of the initial condition (3.4), give (m + 1) of nonlinear algebraic equations which can be solved, for the unknown ci, i = 0,1, …, m.

In the following section, to achieve from the validity and the accuracy we compare our approximate solution with those obtained using the variational iteration method.

4. Procedure of Solution Using VIM

The VIM gives the possibility to write the solution of (1.4), (0 < α ≤ 1) with the aid of the correction functionals in the form:
()
where λ is the general Lagrange multiplier, which can be identified optimally via the variational theory [13]. The function is a restricted variation, which means that . Therefore, we first determine the Lagrange multiplier λ that will be identified optimally via integration by parts. The successive approximations xn, n ≥ 0, of the solution x(t) will be readily obtained upon using the obtained Lagrange multiplier and by using any selective function x0. The initial values of the solution are usually used for selecting the zeroth approximation x0. With λ determined, several approximations xn,   n ≥ 0, follow immediately. Making the above correction functional stationary:
()
where is considered as a restricted variation, that is, , yields the following stationary conditions (by comparison the two sides in the above equation):
()
The equation in (4.3) is called Lagrange-Euler equation with the natural boundary condition. The solution of this equation gives the Lagrange multiplier λ(τ) = −1.
Now, by substituting in (4.1), we obtained
()

5. Procedure of Solution Using VIM with Fractional Complex Transform

In this section, we use the fractional complex transform [23, 24] to convert the fractional Logistic equation into its differential partner, so that the VIM can be effectively used. To achieve this aim we can use the following fractional complex transform:
()
and using Jumarie′s chain rule [37, 38], we have
()
So, we can obtain the corresponding ordinary differential equation of (1.4) as follows:
()
The variational iteration algorithm is
()
We start with initial approximation x0(t) = 0.5, and by using the above iteration formula (4.4), we can directly obtain the components of the solution. Consequently, the exact solution may be obtained by using the following:
()
Now, the first two components of the solution x(t) at α = 1, ρ = 0.5 of the fractional Logistic equation with different two delays by using (4.4) or (5.4) are
  •  

    x0(t) = 0.5,

  •  

    x1(t) = 0.5 + t4 + 0.0555556  t9, ….

The numerical results of this example are presented in Figures 1–5, using the Chebyshev collocation method (ChebM) and compared with the approximate solution using VIM. We considered different values of the delay parameters r1 and r2 with different values of m and α.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
The behavior of the numerical solution (at α = 1, ρ = 0.5) using ChebM with (m = 6) and VIM at r1 = 0.0, r2 = 0.7 (a) and r1 = r2 = 0.7 (b).
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
The behavior of the numerical solution (at α = 1, ρ = 0.5) using ChebM with (m = 6) and VIM at r1 = 0.0, r2 = 0.7 (a) and r1 = r2 = 0.7 (b).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The behavior of the numerical solution (at α = 1, ρ = 0.5) using ChebM with (m = 6) and VIM at r1 = 0.7, r2 = 0.7.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
The behavior of the numerical solution (at α = 0.85, ρ = 0.5) using ChebM with (m = 6) at r1 = 0.0, r2 = 0.7 (a) and r1 = r2 = 0.7 (b).
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
The behavior of the numerical solution (at α = 0.85, ρ = 0.5) using ChebM with (m = 6) at r1 = 0.0, r2 = 0.7 (a) and r1 = r2 = 0.7 (b).
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Show phase portrait of the system, that is, plot of x(t) versus x(t − r1) (a) and plot of x(t) versus x(t − r2) (b) at r1 = 0.7, r2 = 0.7, and α = 0.85.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Show phase portrait of the system, that is, plot of x(t) versus x(t − r1) (a) and plot of x(t) versus x(t − r2) (b) at r1 = 0.7, r2 = 0.7, and α = 0.85.
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Show phase portrait of the system, that is, plot of x(t) versus x(t − r1) (a) and plot of x(t − r1) versus x(t − r2) (b) at r1 = 0.7, r2 = 0.7, and α = 0.85.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Show phase portrait of the system, that is, plot of x(t) versus x(t − r1) (a) and plot of x(t − r1) versus x(t − r2) (b) at r1 = 0.7, r2 = 0.7, and α = 0.85.

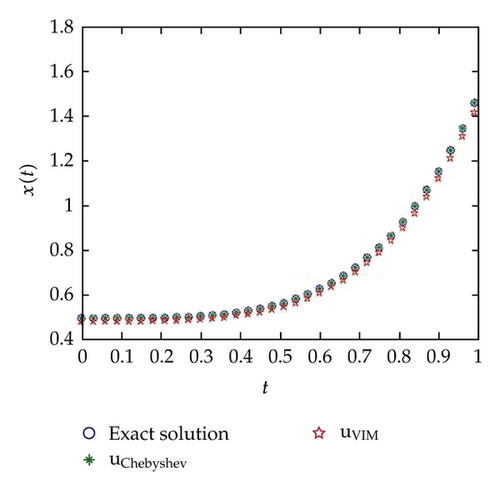
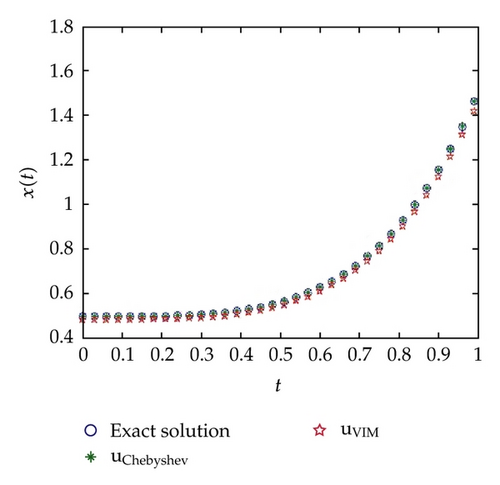
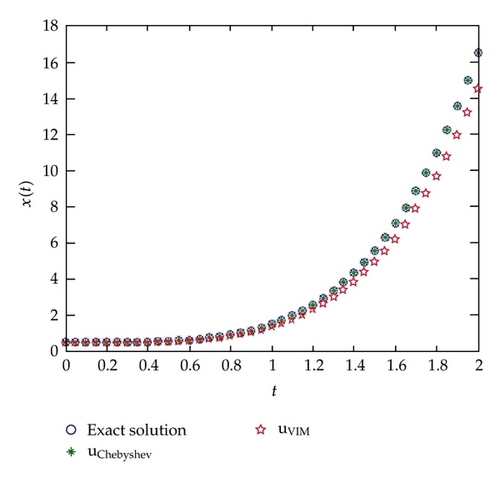
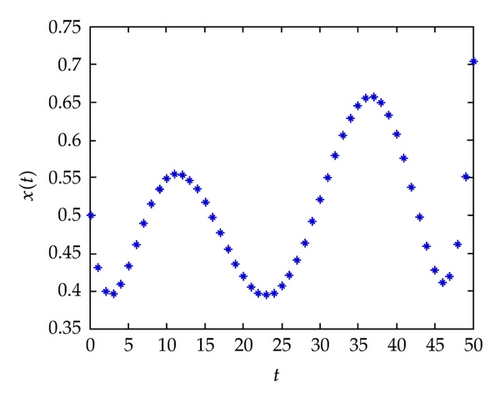
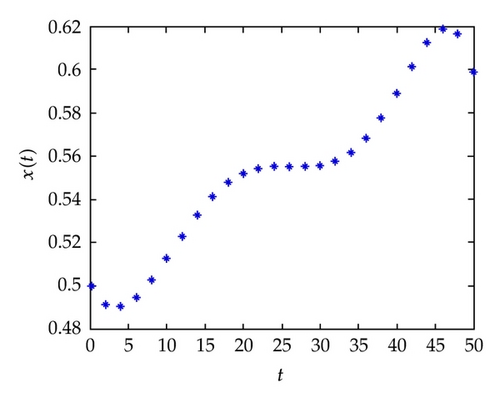
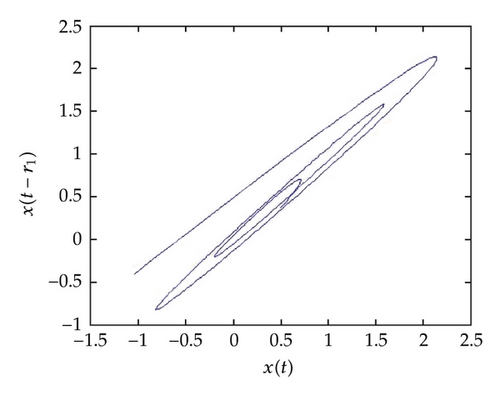
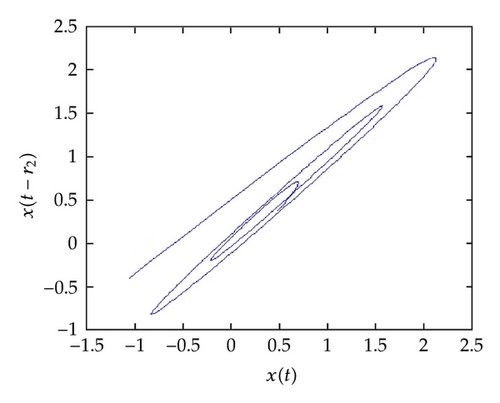
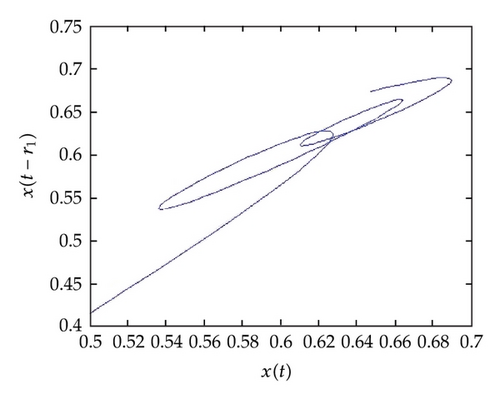
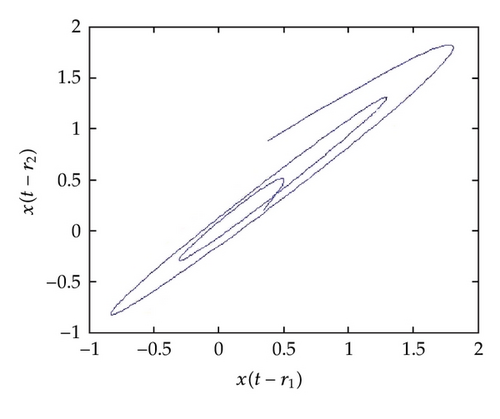
In Figure 1, the behavior of the numerical solution (at α = 1, ρ = 0.5) using ChebM with (m = 6) and VIM at r1 = 0.0, r2 = 0.7 (a) and r1 = r2 = 0.7 (b) is presented in the interval [0,1]. In Figure 2, the behavior of the numerical solution (at α = 1, ρ = 0.5) using ChebM with (m = 6) and VIM at r1 = 0.7, r2 = 0.7 is presented in the interval [0,2]. In Figure 3, the behavior of the numerical solution (at α = 0.85, ρ = 0.5) using ChebM with (m = 6) at r1 = 0.0, r2 = 0.7 (a) and r1 = r2 = 0.7 (b) is presented in the interval [0,10]. Also, from Figures 4 and 5 we can see that the system shows a periodic (chaotic) behavior. In the above experiments we have decreased the value of α and observed that the system becomes periodic for α.

In Table 1, we presented the CPU time needed for the computation with each method using different values of m, where m represents the iteration number of VIM and represents the number of term of the series using the ChebM.

Table 1. The CPU time needed for the computation with each method.
m ChebM VIM
3 2.3 s 1.5 s
5 4.0 s 2.8 s
7 5.8 s 4.6 s

From Figure 1, we can conclude that the obtained numerical results using the proposed method are in excellent agreement with the exact solution and the solution using VIM. On the other hand, in Figure 2, we saw that the solution using VIM is not agreement with the exact solution at a large domain. This result confirm that our proposed method is more accurate and efficiency from VIM.

6. Conclusion

In this paper, some interesting fractional delay differential equations arising in biology have been solved. It is observed that even two dimensional delayed systems of fractional order show chaotic behavior, and below some critical order, the system changes its nature and becomes periodic. In some cases it is observed that the phase portrait gets stretched as the order of the derivative is reduced. We used two computational methods, Chebyshev spectral method and variational iteration method for solving the fractional-order Logistic equation with two different delays. We derived an approximate formula of the fractional derivative. The properties of the Chebyshev polynomials are used to reduce FOLE with two different delays to the solution of nonlinear system of algebraic equations. Special attention is given to study the convergence analysis and estimate the upper bound of the error of the derived formula. From the solutions obtained using the suggested method we can conclude that these solutions are in excellent agreement with the exact solution and show that these approaches can solve the problem effectively. It is evident that the overall errors can be made smaller by adding new terms from the series (2.7). Comparisons are made between approximate solutions to illustrate the validity and the great potential of the proposed techniques. All numerical results are obtained using MatLab 8.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.