Journal of Applied Mathematics
Volume 2012, Issue 1 763849
Research Article
Open Access

Simplified Analytical Method for Estimating the Resistance of Lock Gates to Ship Impacts

Loïc Buldgen, 

Corresponding Author

Loïc Buldgen

Faculty of Applied Sciences and ANAST, University of Liège, 1 Chemin des Chevreuils, 4000 Liège, Belgium ulg.ac.be

Search for more papers by this author
Hervé Le Sourne, 

Hervé Le Sourne

Mechanical Engineering Department (LE2M), ICAM Nantes Campus, 35 avenue du Champ de Manœuvres, 44470 Carquefou, France icam.fr

Search for more papers by this author
Philippe Rigo, 

Philippe Rigo

Faculty of Applied Sciences and ANAST, University of Liège, 1 Chemin des Chevreuils, 4000 Liège, Belgium ulg.ac.be

Search for more papers by this author
First published: 29 May 2012
https://doi.org/10.1155/2012/763849
Citations: 4
Academic Editor: Celso P. Pesce

Abstract

The present paper is concerned with the design of lock gates submitted to ship impacts. In this paper, a simplified analytical method is presented to evaluate the resistance of such structures under collision. The basic idea is to assume that the resistance is first provided through a local deforming mode, corresponding to a localized crushing of some impacted structural elements. For consecutive larger deformations, the resistance is then mostly provided through a global deforming mode, corresponding to an overall movement of the entire gate. For assessing the resistance in the case of the local deforming mode, the structure is divided into a given number of large structural entities called “superelements.” For each of them, a relation between the resistance of the gate and the penetration of the striking ship is established. However, as some results are already available in the literature, this subject is not treated extensively in this paper. On the contrary, the calculation of the resistance of the gate provided through the global mode is detailed and the strategy to switch from local to global deformation is highlighted. Finally, we propose to validate our developments by making a comparison between results obtained numerically and those predicted by the present analytical approach.

1. Introduction

Amongst all the loads that have to be expected for the design of lock gates, the collision of a vessel is one of the most difficult to handle.

A collision may result in some minor damages to the plating or to the stiffening system of the gate, producing, for example, a local loss of water tightness. However, if the initial velocity of the striking ship is large enough, the displacements imposed to the structure may cause a complete collapse of the gate. This would result in the emptying of the damaged reach, with probably the complete sinking of the striking ship.

To deal properly with ship impact, it is of course possible to use nonlinear finite element methods. Nevertheless, at the predesign stage of a gate, such approaches are rather restrictive because of the time required to model and simulate collisions. Therefore, we propose here to establish an analytical simplified method in order to verify the resistance of gates submitted to a ship impact.

For the moment, the development of such simplified methods is not really reported in the literature. Some very interesting results have been established for the purpose of analyzing collisions between two ships. For example, the crushing resistance of web girders has already been theoretically and experimentally studied by Wierzbicki and Culbertson Driscoll [1], Wang and Ohtsubo [2], Simonsen [3], Zhang [4], and Hong and Amdahl [5]. Each of them developed analytical formulations that may be useful for studying locally the contact between a ship and a gate.

Additional results are also available for impacted panels, which have been investigated in detail by Wang [6], Wang and Ohtsubo [7], and Zhang [8]. Some references are also useful for evaluating the resistance of metal plates after rupture, when they are submitted to tearing and cutting. For example, these phenomena have been studied by Wang and Ohtsubo [7], Zhang [8], Wierzbicki [9], and Zheng [10]. In the particular case of stiffened panels subjected to lateral loads, the developments performed by Paik [11], Cho and Lee [12], or Ueda et al. [13] constitute a very accurate basis for performing analytical estimation of the resistance of such structural components.

The previous brief literature review shows that some results are already available to deal with a simplified approach of collisions between ships and gates. All these developments constitute of course an invaluable help for developing simplified collision models of lock gates, but they are not sufficient. The principal reason is that the behavior of an impacted gate may not directly be assimilated to the one of an impacted vessel. Consequently, some researches in this domain are still needed.

The aim is to develop some analysis tools, which would be time and cost-effective in the predesign stage of gates. To achieve this goal, we will follow a similar method to the one proposed by Le Sourne et al. [14]. The basic idea is that the total resistance of the struck gate is provided by two deforming modes:
  • (i)

    the local one, which implies a local crushing of all the impacted structural elements;

  • (ii)

    the global one, which supposes an overall deformation of the gate.

In the present paper, we try to go further into this philosophy.

2. General Description of the Problem

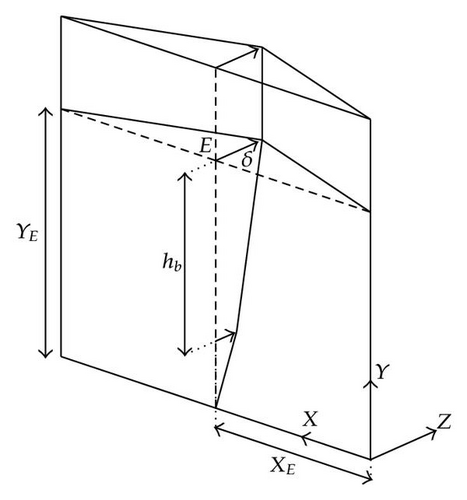
In this paper, we consider the exceptional situation of ship colliding with a lock gate. The collision scenario is depicted in Figure 1, where the general coordinate system is denoted by (X, Y, Z). For avoiding confusion in the present paper, we will use the terminology “transversal,” “vertical,” and “longitudinal” in accordance with the respective orientation of X, Y, and Z axes.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Plane and section views of the impact situation.

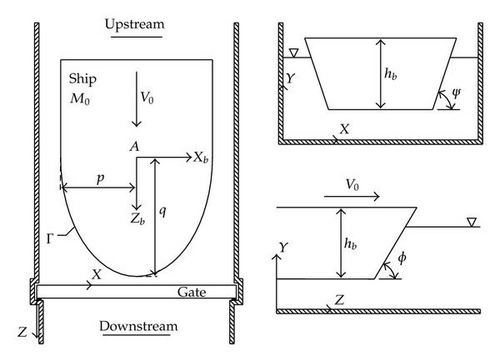
In our scenario, the vessel is coming from upstream, and, consequently, the impact is located on the downstream gate of the lock. It is clear that this case is the least desired because the hydrostatic pressure is acting in the same direction as the impact force. On the contrary, if the collision was happening in the downstream reach of the lock, the resulting hydrostatic pressure would act in opposition with the impact force and would compensate it partially.

In order to derive an analytic procedure for estimating the collision resistance of the gate, we first need to describe the ship and the gate using various parameters. This is the purpose of the subsequent sections.

2.1. Geometrical Description of the Striking Vessel

The vessel is characterized through the following: mass M0 and velocity V0. In other words, we assume a certain kinetic energy for the striking ship. These two parameters are chosen according to the waterway class, which determines the maximal speed as well as the allowable shipping of the vessels.

From the geometric point of view, we first assume that the shape of the bow at the uppermost deck may be fairly modeled by a parabola Γ (see Figure 1) having a transversal radius p and a longitudinal radius q. Consequently, in the local axes (xb, zb) positioned in point A, the equation of the curve Γ is given by
(2.1)
In order to have a global description of the geometry of the ship, it is also required to introduce the following parameters (see also Figure 1):
  • (i)

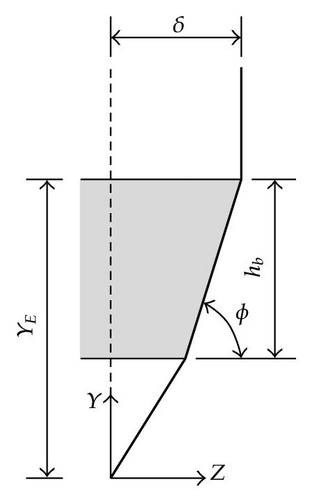
    the height hb between the uppermost deck and the bottom of the ship;

  • (ii)

    the side angle ψ and the stem angle ϕ, which are used to fix the inclination of the bow.

It is important to note that all the above mentioned properties are required input data, which have to be provided by the user before the beginning of the calculation process.

2.2. Description of the Gate

In this paper, we will only focus on gates with a single plating. A three-dimensional picture of such a structure is depicted in Figure 2, where the notations H and L are used for representing, respectively, the total vertical and the total transversal extension of the gate. In fact, these gates are rather similar to large orthotropic plates, constituted by a plating (for retaining water) stiffened by the following elements (see Figures 2 and 3):
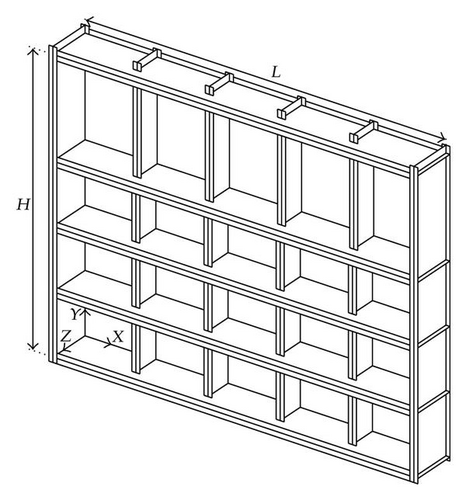
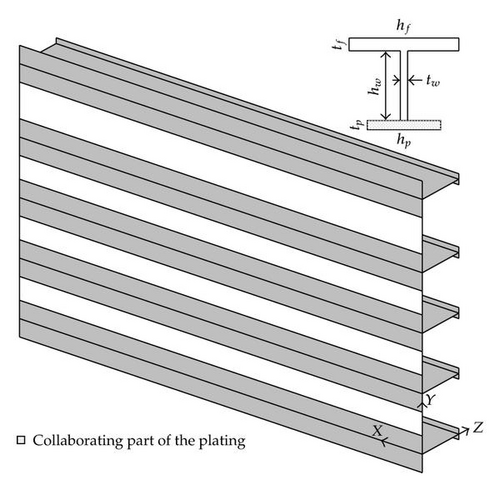
  • (i)

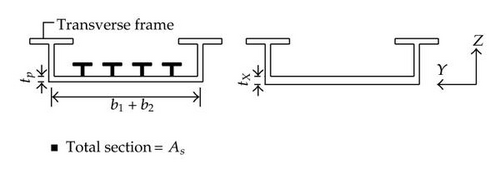
    the transversal frames, which may be seen as beams presenting a T-shaped cross-section; they are placed in the transversal direction (i.e., along the X axis);

  • (ii)

    the vertical frames, which are also beams with a T-shaped cross-section but are arranged in the vertical direction (i.e., along the Y axis);

  • (iii)

    the stiffeners, which are optional reinforcing beams disposed transversally on the plating in order to avoid instabilities in shells; their cross-section may exhibit various shapes.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Three-dimensional representation of the considered type of gate.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Plan and section views of the gate.

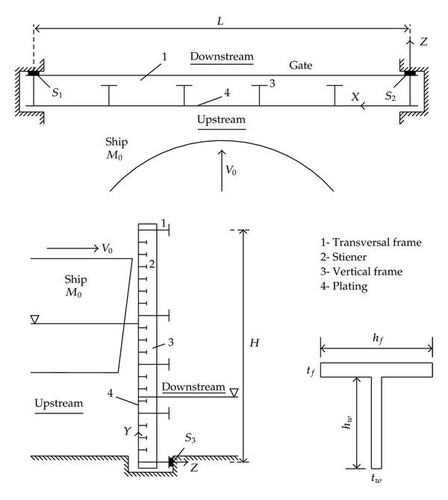
The geometric data required for characterizing the stiffening system are mainly the dimensions of the different cross-sections. As shown in Figure 3, the needed values are the height hw and thickness tw of the web, as well as the height hf and thickness tf of the flange. For the plating, it is only necessary to precise its thickness tp. With all these parameters and knowing the properties of the material constituting the gate, it is possible to derive the mechanical properties of all the stiffening elements.

Another point that has to be clarified concerns the assumed support conditions of the structure. When the gate is closed, the contact is supposed to be established against the support denoted by S1, S2, and S3 in Figure 3, and, consequently, we may admit that:
  • (i)

    the gate is simply applied against the two lock walls (supports S1 and S2 in Figure 3). The translational degree of freedom in the Z direction has therefore to be blocked along the all vertical extensions of the gate in S1 and S2;

  • (ii)

    the gate is simply applied against the sill located at the bottom of the chamber (support S3 in Figure 3). Therefore, it seems to be reasonable to restrain the translational displacement in the Z direction along the all transversal extension of the gate in S3.

2.3. Description of the Material

The present paper is concerned with the resistance of a lock gate impacted by a ship. The primary goal is not to assess the damages caused to the vessel: we are much more interested in the ability aspect of the structural resistance to collisions. As a consequence, we assume that the material constituting of the striking vessel is infinitely rigid. In other words, we will not allow any deformation in the ship structure, which is a conservative approach in the evaluation of the resistance.

On the contrary, the previous hypothesis is not valid for the gate as it is supposed to be deformable. Nowadays, the most common material used for such structures is construction steel, so we will only deal with this material in the present paper. This kind of steel exhibits a constructive law represented by curve (1) in Figure 4 and may be defined by the following parameters:
  • (i)

    the maximal elastic stress σ0, with which is associated the maximal elastic deformation ϵ0;

  • (ii)

    the rupture stress σu, for which tearing is observed in the material; the corresponding deformation is called ϵu;

  • (iii)

    Young’s modulus E characterizing the stiffness of the material during the elastic phase.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Real (1) and idealized (2) constitutive law of standard construction steel.

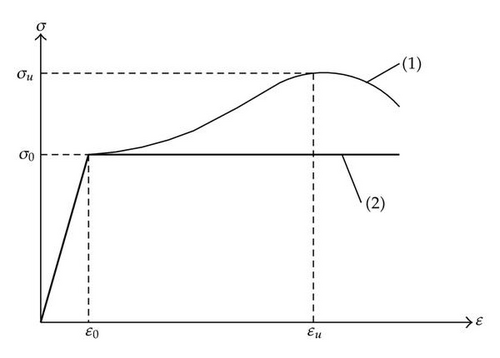
In order to simplify the analytical derivation of the collision resistance, we will suppose here that the steel has a so-called elastic-perfectly plastic behavior. This means that the relation between stresses and strains is idealized by curve (2) in Figure 4. Consequently, we neglect the additional resistance coming from hardening of steel, which is in fact a conservative assumption.

2.4. General Positioning in the Space

To define the collision scenario, it is still necessary to position the resistance element as well as the striking ship within the area of space. To do so, different kinds of input data are still required:
  • (i)

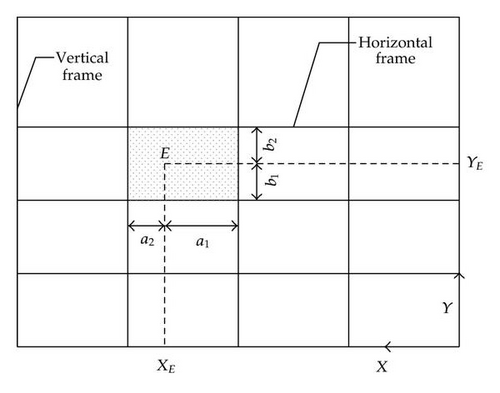
    the impact point E, that is, the point of the gate where the first contact between the bow and the plating will be established; this point is located by its coordinate (XE, YE), as shown in Figures 5 and 6;

  • (ii)

    the transversal positions Xi of the vertical frames, that is, the position of each vertical frame along the X axis (see Figure 5);

  • (iii)

    the vertical positions Yi of the horizontal frames, that is, the position of each horizontal frame along the Y axis (see Figure 5);

  • (iv)

    the total number of stiffeners distributed along the vertical height H of the gate.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Position of the resistance elements and of the impact point.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Representation of the impact force.

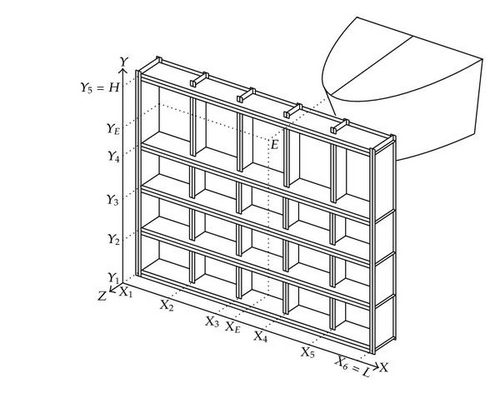
When all the previous inputs are placed, the three-dimensional configuration of the gate is completely defined.

3. Methodology for Evaluating the Collision Resistance

3.1. General Principles

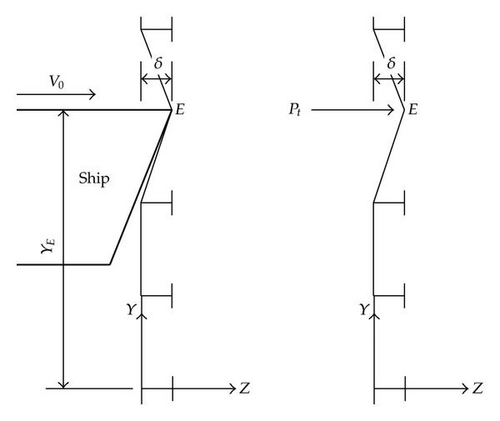
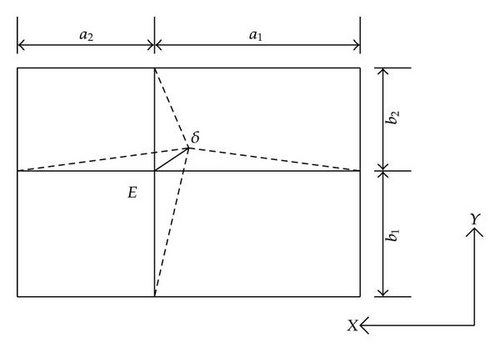
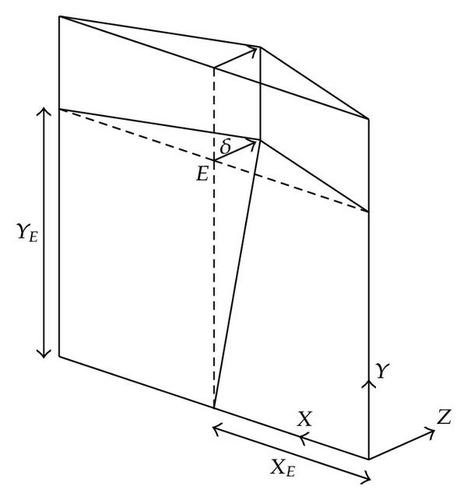
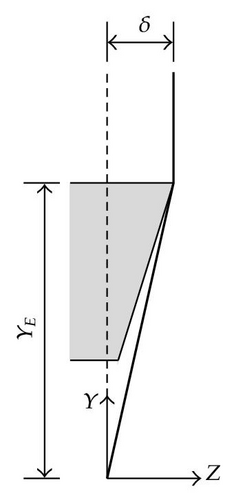
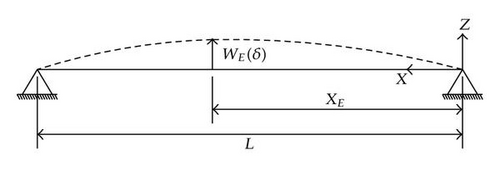
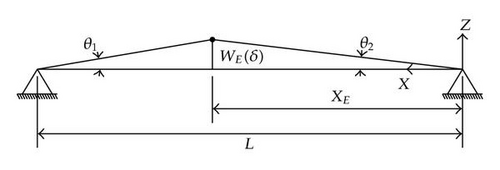
When a ship collides with a gate, its action on the impacted structure may be represented by a force Pt acting in the same direction as the indentation δ of the striking vessel (see Figure 6). By equilibrium, this force may be seen as the resistance opposed by the gate to the progression of the ship. Therefore, the goal of our work is to assess the value of Pt for a given indentation δ of the vessel. In other words, our aim is to derive the evolution of Pt with δ by means of simplified analytical procedures.

When a ship is entering into a lock, it seems reasonable to admit that its initial velocity V0 is quite small. Consequently, the dynamic effects in the gate remain moderate, and we may assume that the initial kinetic energy of the ship is entirely dissipated by deformation of the impacted gate Eint , that is,
(3.1)
Knowing the relation between Pt and δ, it is possible to calculate Eint  simply by integration (see Figure 7):
(3.2)
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Evolution of the resistance of the gate with the penetration of the ship.

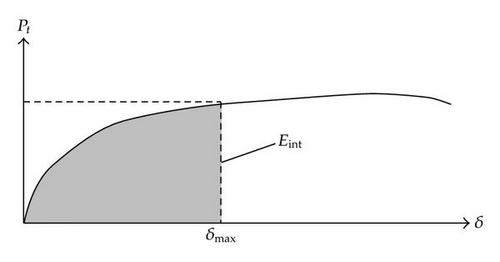
For a given ship of mass M0 and velocity V0, (3.1) and (3.2) give the maximal penetration δmax , which has to be supported by the gate to withstand an impact with such a vessel. According to the maximal degradation level accepted for the gate, it can be decided if this value of δmax  may be applicable or not.

3.2. Theoretical Basis

The theoretical basis for deriving Pt(δ) is the so-called upper-bound theorem, which states that “if the work rate of a system of applied loads during any kinematically admissible collapse of a structure is equated to the corresponding internal energy dissipation rate, then that system of loads will cause collapse, or incipient collapse, of the structure.”

In the present case, it is obvious that the external dissimilation rate is entirely produced by the force Pt applied by the ship on the gate. Therefore, we have
(3.3)
where is the derivative with respect to time. On the other hand, if we neglect the dynamic effects in the structure, the internal dissipation rate is entirely coming from the deformation of the gate. If 𝒱 is the total volume of the structure, using Einstein’s notation we have:
(3.4)
where σij and are, respectively, the stress and the strain rate tensors defined over the entire volume 𝒱 of the gate. By application of the upper-bound theorem, we have
(3.5)

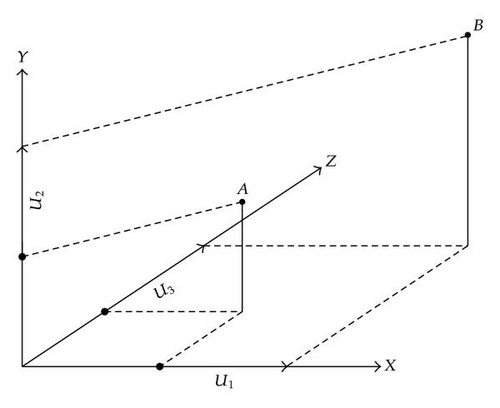
Consequently, (3.5) may be useful for deriving Pt(δ), provided that we are able to establish a relation between the deformation rate and the velocity . To do so, we need to define the displacements over the entire volume 𝒱. For example, in Figure 8, if we suppose that point A is moving to point B for a given value of δ, we may define the three components U1(X, Y, Z, δ), U2(X, Y, Z, δ), and U3(X, Y, Z, δ) of the displacement field along axis X, Y, or Z, respectively. Note that in the remaining part of this paper, we will also use the equivalent notations (U, V, W) and (X1, X2, X3) for designating (U1, U2, U3) and (X, Y, Z).

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Definition of the displacement field.
Using the Green-Lagrange tensor, it is finally possible to find a link between the deformation and the penetration of the ship δ:
(3.6)
Equation (3.6) may be rewritten in the following shorter form:
(3.7)
If we want to apply formula (3.5) to obtain a relation between Pt and δ, it is also required to evaluate the stresses σij as a function of δ. This may be achieved using the constitutive laws giving a relation between σij and ϵij. As the evolution of ϵij with δ is known by (3.6), we also have
(3.8)
Note that U1, U2, and U3 are unknown; for a given value of δ, we have to postulate a certain displacement field. Provided that this displacement field is kinematically admissible, we may apply the upper-bound theorem and calculate the resistance Pt with formula (3.5). In fact, if we combine (3.7) and (3.8) in (3.5), we obtain
(3.9)

Equation (3.9) is the needed relation between Pt and δ. However, the crucial point in the above-described approach is to define properly a kinematically admissible displacement field, otherwise the upper-bound theorem may lead to an overestimation of the crushing resistance.

3.3. The Superelements Method

The integration of (3.9) has to be performed over the whole volume 𝒱 of the struck structure and is rather impossible to derive analytically. As a consequence, we need to simplify the procedure described here over, and this may be achieved by splitting the gate into superelements.

The basic idea is to divide the gate into different substructures (the so-called superelements) that we assume working independently. For the lock gate depicted in Figure 2, the structure may be decomposed into two types of superelements.
  • (i)

    The first superelement (SE1) is a rectangular plate simply supported on its four edges and impacted perpendicularly to its plane, undergoing therefore important out-of-plane displacements. Such elements are typically used for modeling the plating of the gate.

  • (ii)

    The second superelement (SE2) is a beam with a T-shaped cross-section, impacted in its plane. This kind of element is therefore quite relevant for modeling transversal and horizontal frames.

The division of the gate into superelements is only based on geometric considerations. In order to illustrate this process, we can consider, for example, only a small part of the lock gate represented in Figure 2, for which the division principle is shown in Figure 9. As it can be seen, the two previous types of elements are sufficient for analyzing the structure.

Details are in the caption following the image
Figure 9 (a) 2 SE1’s are used for modeling the plating
Open in figure viewerPowerPoint
Illustration of the subdivision of a structure into superelements.
Details are in the caption following the image
Figure 9 (b) 3 SE2’s are used for modeling the vertical frames
Open in figure viewerPowerPoint
Illustration of the subdivision of a structure into superelements.
Details are in the caption following the image
Figure 9 (c) 2 SE2’s are used for modeling the transversal frames
Open in figure viewerPowerPoint
Illustration of the subdivision of a structure into superelements.
As long as there is no contact between the ship and a given superelement, this latter will remain inactive. This means that it will not deform until it has been collided by the bow, which is a consequence of the above-mentioned hypothesis that each substructure is working independently. After being activated, the superelement will deform and dissipate a certain amount of energy. If the gate is divided into n superelements, as each of them is decoupled from the others, the total internal energy Eint  is simply obtained by summation of the individual contributions coming from the n superelements, that is,
(3.10)
where is the internal energy dissipated by superelement number k for a given penetration δ of the ship. Before using (3.10), it is preliminary required to know . To do so, formula (3.4) is still valid, but it has to be reequated for the case of superelement k:
(3.11)
where we have introduced the following notations:
  • (i)

    is the stress tensor defined on the entire volume of superelement k,

  • (ii)

    is the strain rate tensor defined on the entire volume of superelement k,

  • (iii)

    𝒱k is the volume of superelement k.

By following a similar reasoning as for relations (3.7) and (3.8), we get finally the particularization of (3.9):
(3.12)
where may be seen as the contribution of superelement k to the total resistance of the gate (note that Einstein’s notation has been used for the subscripts i and j). In fact, relation (3.12) is of primary importance because it constitutes the fundamental basis of the present method. Of course, we still need to develop adequately the functions involved in this expression. This will be done later for SE1 and SE2.

3.4. Global and Local Deforming Modes

We previously assumed that each superelement was working independently from the others. This hypothesis remains valid as long as the penetration δ is reasonably minor. However, when the penetration δ of the ship is increasing, deformations will occur in superelements that still have not been undertaken by the bow. Consequently, the internal energy rate for superelement k may not be equal to zero, although it has not been activated. This may be seen on Figure 10, where out-of-plane displacements occur in the entire gate, even if some regions have not been impacted by the striking ship bow.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Illustration of global and local deformations.
In order to take this coupling into account, let us introduce the concept of local and global deforming modes.
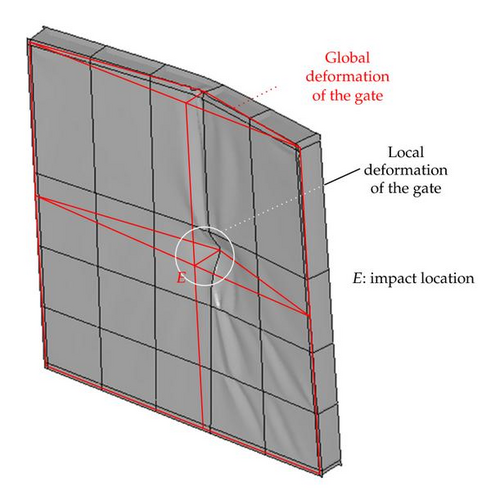
  • (i)

    We say that the structure exhibits a local deforming mode (see Figure 10) when the developments performed in Section 3.3 may be applied. In other words, we suppose here that the penetration of the vessel into the gate is only allowed by the local deformations of the activated superelements. Only the area impacted by the ship contributes to the energy dissipation; the other parts of the gate remain undeformed. Of course, it may be easily understood that the local mode is only valid for quite small values of δ.

  • (ii)

    On the contrary, we say that the structure exhibits a global deforming mode (see Figure 10) when the displacements are not confined in a small area located around the impact point. In this case, the entire gate is involved in the energy dissipation process and we may no longer assume that it behaves like a set of independent substructures activated progressively. Consequently, the superelements method is not valid anymore and the resisting force Pt has to be evaluated by another way than the one discussed in Section 3.3. This is precisely the topic of Section 5.

In order to model the phenomena depicted in Figure 10, we suppose that there is a sudden switch between the two modes. At the beginning, when the striking ship starts moving into the gate, the resistance Pt is essentially provided by the local deforming mode. This statement remains valid as long as the penetration δ does not exceed a transition value δt, for which the global mode is activated. In fact, the switch between the two modes occurs when the force Pt applied by the ship on the gate is sufficient to cause an overall displacement of the whole structure. As soon as δ ≤ δt two different values for Pt are computed:
  • (i)

    the value of Pt obtained by supposing a local deforming mode; it is denoted by Ploc ;

  • (ii)

    the value of Pt obtained by supposing a global deforming mode; it is denoted by Pglob.

For a given penetration δ, Ploc  and Pglob are then compared. As long as Ploc  < Pglob, the force exerted locally by the ship is not sufficient to cause an overall displacement of the gate, so the ship continues penetrating into the structure by local indentation. However, as soon as Ploc  = Pglob, the force becomes sufficient and the switch from the local mode to the global one is obtained. The corresponding value of δ is the required δt (see Figure 11). After that, for the values of δ greater than δt, the resistance Pt is evaluated using equations specially developed for the global mode (see Section 5).

Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
Evaluation of the transition from the local to the global mode.

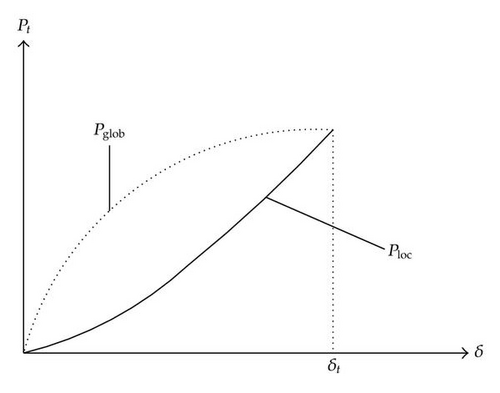
4. Evaluation of the Resistance in the Local Deforming Mode

In the local deforming mode, the resistance of the gate is given by (3.12), where we assume that the total resisting force is simply obtained by adding the individual contributions of all the activated substructures. In this section, the laws governing the behavior of the two types of superelements introduced in Section 3.3 are detailed. However, as this topic is already well treated in the literature (see e.g., [4]), in order to avoid any redundancy, we have made a quite concise presentation of our approach.

Note In the two following sections, we will use the superscript (k) for characterizing any property of the superelement number k.

4.1. Superelement Type 1 (SE1)

The first superelement is used for modeling the plating of the lock gate. Its boundaries are defined by the surrounding transversal and vertical frames, as shown in Figure 12. Considering the location of the impact point E, it is possible to fix the four parameters , , , and .

Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
Definition of the main dimensions of SE1.
The thickness of the plate is equal to the thickness tp of the plating. However, a correction is needed for taking into account the horizontal stiffeners placed in the transversal direction. During the collision, the stiffeners are mainly submitted to an axial extension; they will deform along the X direction by exhibiting a membrane behavior. Consequently, the plate thickness has to be modified for taking these effects into account. If As is the total area of all the stiffeners connected to the superelement k (see Figure 13), then we obtain
(4.1)
Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
Equivalent plate thickness.

This correction has to be applied for the calculation of membrane effects in the X direction. However, if we consider membrane effects in the Y direction, the stiffeners have no influence and they do not need to be considered. Consequently, we have and the plate becomes orthotropic.

In the present approach, we suppose that the impacted plate is completely independent from the surrounding other superelements. Therefore, it is acceptable to consider the plate as simply supported on its four edges. For a given indentation δ, the superelement will undergo mostly a membrane deformation; the effects of bending remain negligible.

When superelement SE1 is impacted by the bow of the vessel, for a given value of δ, we may deduct the deformation pattern shown in Figure 14. With this displacements field, it is possible to evaluate the internal energy rate, which has already been done by Zhang [4].

Details are in the caption following the image
Figure 14
Open in figure viewerPowerPoint
Displacement field assumed for SE1.
For the situation illustrated in Figure 14, Zhang [4] found the following crushing resistance for superelement k:
(4.2)

4.2. Superelement Type 2 (SE2)

The second superelement that we will consider is used for modeling the transversal and vertical frames. The boundaries of a horizontal superelement are defined by the two adjacent vertical frames (and inversely for a vertical superelement).

The principal dimensions and (see Figure 15) of superelement k are positioned in accordance with the location of the impact point. The resisting cross-section has a T-shape, whose properties are defined in the general geometry of the gate.

Details are in the caption following the image
Figure 15
Open in figure viewerPowerPoint
Definition of the main dimensions of SE2.

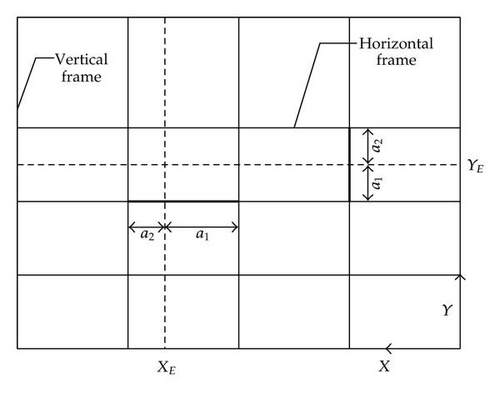
When this superelement is impacted, we suppose that it will deform like a concertina. To do so, three plastic hinges are formed. They are designated by ABF, ACF, and ADF in Figure 16. These lines allow for relative rotation between the triangular surfaces ABC, ACD, BCF, and FCD. Bending effects are therefore preponderant along these lines.

Details are in the caption following the image
Figure 16
Open in figure viewerPowerPoint
Displacements field assumed for SE2.

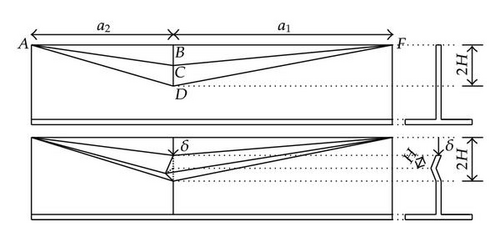
However, the rotational movement of the triangular surfaces is not free because it must respect the compatibility between surfaces ABD and BFD along their common line BD. Therefore, surfaces ABD and BFD are submitted to an axial extension implying mainly membrane effects. Consequently, for a given indentation δ, the web will be folded as represented in Figure 16, where 2H is the total height of one fold. According to the previous hypothesis, during this motion, the energy is absorbed by membrane extension of the triangular regions ABD and BFD, but also by bending effects in the three plastic hinges ABF, ACF, and ADF. The phenomenon of concertina folding has already been studied by a great number of authors. For example, it was theoretically and experimentally studied by Wierzbicki and Culbertson Driscoll [1], Wang and Ohtsubo [2], Simonsen [3], and Zhang [4]. Hong and Amdahl [5] compared all these various approaches and also developed their own model.

According to the developments performed by Zhang [4], for a given penetration δ, the resistance of superelement number k is to be taken as
(4.3)
where is the web thickness of superelement k. In this formula, H is a parameter fixed by minimizing the mean crushing resistance over one fold. By so doing, Zhang [4] found that
(4.4)

4.3. Total Resistance in Local Deforming Mode

The total resistance of the gate in the local deforming mode is simply obtained by summing the individual contributions of the n superelements:
(4.5)
Of course, for a given value of δ, if a superelement has not been activated, it will not provide any resistance to the total resistance, and so we have
(4.6)

5. Evaluation of the Resistance in the Global Deforming Mode

5.1. Displacements Fields

When the global mode is activated, the gate is assumed to undergo a global motion involving the entire structure. The displacements field obtained in this case is plotted in Figure 17(a). As mentioned earlier, the first contact between the bow and the plating is located in point E, with coordinates (XE, YE, 0). In the vertical plan passing through this point (i.e., the plan with equation X = XE), we suppose that the displacements are distributed along the vertical Y axis as shown in Figure 17(b). The mathematical formulation of this profile is as follows:
(5.1)
where WE indicates that we consider the displacement in the plan X = XE.
Details are in the caption following the image
Figure 17 (a)
Open in figure viewerPowerPoint
(a) Assumed displacements field. (b) Displacement profile in the plan X = XE.
Details are in the caption following the image
Figure 17 (b)
Open in figure viewerPowerPoint
(a) Assumed displacements field. (b) Displacement profile in the plan X = XE.
The two previous formulae are only valid as long as there is no other contact between the ship and the gate. However, as the vessel is moving forward, another contact will appear between the plating and the lowermost deck (see Figure 18). The particular value of δ for which this situation will occur is denoted by δc, and we have
(5.2)
where ϕ is the stem angle. When δ ≥ δc, the contact between the bow and the plating is completely developed along the height hb (see Figure 18). Consequently, it is required to adapt the previous displacements fields in order to account for this phenomenon. Then, for δ ≥ δc, we will use the following equations:
(5.3)
Details are in the caption following the image
Figure 18 (a)
Open in figure viewerPowerPoint
Assumed displacements field after second contact between the bow and the plating.
Details are in the caption following the image
Figure 18 (b)
Open in figure viewerPowerPoint
Assumed displacements field after second contact between the bow and the plating.

5.2. Mechanical Model of the Gate

In the previous section, we have postulated a kinematically admissible displacements field. In accordance with the upper-bound method, it is now possible to use the principle of virtual velocities in order to estimate the resistance of the structure deformed in the global mode.

Unfortunately, it is rather difficult to derive analytically the resistance of a gate submitted to the displacements given by (5.1), (5.3). In order to simplify the problem, we make the assumption that the main contribution to the resistance is coming from the bending of the gate between the two lock walls. This hypothesis seems to be reasonable for a global mode, especially when the ratio H/L is wide, but we have to bear in mind that it may not remain valid in some special cases. As a consequence, the resistance in the global deforming mode is mostly provided by transversal frames, the stiffeners. Therefore, the gate may be seen as a set of independent beams subjected to a given displacements field. The contribution of the vertical frames is only to apply the expected displacements to these beams; we suppose that they do not take part mechanically in the resistance. According to these hypotheses, we obtain the equivalent model of the gate depicted in Figure 19.

Details are in the caption following the image
Figure 19
Open in figure viewerPowerPoint
Mechanical model of the gate for assessing the resistance in the global deforming mode.
The previously mentioned beams have a cross-section obtained by taking the gross cross-section of the transversal frames, to which the collaborating part of the plating is added (see the picture at the top of Figure 19). The values of hf, tf, hw, tw, and tp are defined as an input of the calculation process, but the collaborating length bf has to be chosen in order to account for the following phenomena:
  • (i)

    the shear lag effect occurring at the junction between the plating and webs of transversal frames;

  • (ii)

    the overall buckling of the stiffened panel located between two transversal frames; this situation corresponds to the configuration (a) plotted in Figure 20.

  • (iii)

    the local buckling of the plating located between two stiffeners; this is illustrated by the configuration (b) in Figure 20.

Details are in the caption following the image
Figure 20
Open in figure viewerPowerPoint
Calculation of the effective width.

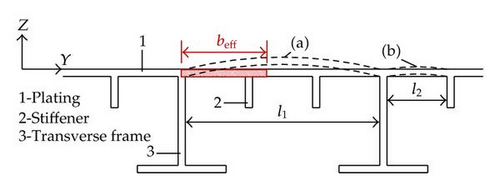
The calculation of the effective width beff (see Figure 20) on both sides of each transversal frame can be achieved by applying the rules provided by Eurocode 3 for longitudinally stiffened plates.

Finally, in order to achieve the mechanical modeling of the gate, we still have to give some details about the support conditions of the beams. As they are connected to the vertical frames, they will be mostly restrained at two levels:
  • (i)

    a rotational restriction along the transversal X axis, which will hinder the torsional effects in the beams;

  • (ii)

    a translational restriction along the longitudinal Z axis, which will hinder out-of-plane shearing and bending of the beams.

Of course, it is rather difficult to precisely account for these effects in an analytical procedure. As we are not trying to have an accurate resistance of the gate (but a good approximation), it is admissible to consider that each beam is simply supported at both ends. By so doing, we completely omit the additional restrains provided by the vertical frames, which is a conservative hypothesis for evaluating globally the impact resistance.

5.3. Elastic Resistance

The mechanical model presented here is a set of n beams submitted to the displacements fields detailed in Section 5.1. In this section, we use the superscript (k) in order to refer to a particular beam, with k ∈ {1,2 … , n}. At the beginning of the impact, a beam located at any given vertical position Y(k) is deformed according to the classical bending theory (see Figure 21). The deflected shape is then given by a parabola:
(5.4)
where and has been defined in Section 5.1. The curvature χ(k) and the bending moments M(k) are obtained using the two following well-known relations:
(5.5)
where E is the elastic modulus and I(k) is the bending inertia of beam k.
Details are in the caption following the image
Figure 21
Open in figure viewerPowerPoint
Elastic deformation of a transversal frame.
If we only consider the deformation energy arising from the bending of beam k, the internal power defined by (3.4) can be calculated by
(5.6)
By introducing (5.4) into (5.6), the individual contribution of beam k to the elastic resistance of the gate in the global deforming mode is defined by
(5.7)

5.4. Plastic Resistance

Of course, (5.7) remains valid as long as there is no plastic effect in beam k. However, when it is bent beyond its elastic limit, the transversal frame exhibits another kind of behavior, which may be described by using the two following properties:
  • (i)

    : the plastic bending moment of beam k, corresponding to a complete plastic cross- section in bending (see Figure 22(a));

  • (ii)

    : the normal plastic force of beam k, corresponding to a complete plastic cross-section in traction or compression (see Figure 22(b)).

Details are in the caption following the image
Figure 22
Open in figure viewerPowerPoint
Plastic properties of the cross-section.

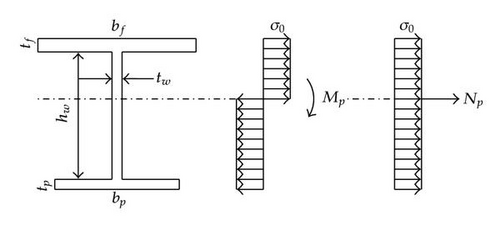
With these properties, a classical plastic analysis may be performed. As soon as is reached, the section located in X = XE behaves like a plastic hinge and the structure becomes a mechanism. At this moment, the yield locus characterizing the cross-section is reached. However, it does not mean that the resistance is not increasing anymore. As the deformations are increasing, tensile stresses appear inside the beam k, and the cross-section is submitted to both a normal force N(k) and a bending moment M(k). As they are linked by the equation of the yield locus, these two actions are not independent.

In order to evaluate M(k) and N(k) for each of the n beams representing the gate, we need more information about plastic interaction. Yukio and Rashed [15] have elaborated a very refined description of the yield locus for the cross-section depicted in Figure 22. However, as suggested by Paik [11], it is easier to adopt a parabolic interaction criterion for beam number k (see Figure 23),
(5.8)
Details are in the caption following the image
Figure 23
Open in figure viewerPowerPoint
Parabolic interaction criterion.
If we note Δ(k) and θ(k), the axial extension and the rotation in beam k, the required condition of normality is verified for the present yield locus if we have (see Figure 23)
(5.9)
The extensional rate and rotational rates and in beam k may be easily calculated by geometrical considerations based on Figure 24:
(5.10)
Details are in the caption following the image
Figure 24
Open in figure viewerPowerPoint
Plastic deformation of a transversal frame.
By introducing (5.10) into (5.9), we finally get a second relation between M(k) and N(k). We then obtain the classical formula giving the membrane force in an axially restrained beam:
(5.11)

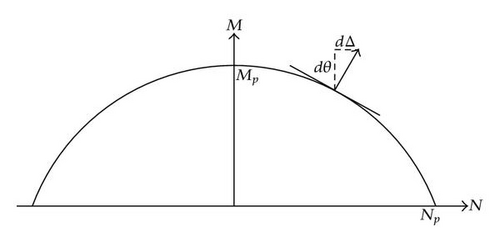
At this stage, it is important to note that this result implies that the beam is perfectly restrained in the axial direction. This hypothesis implies that no transversal motions (along direction X) occur at the supports where X = 0 and X = L. This seems quite reasonable for the gate under consideration because of the action of vertical frames. However, it is important to keep in mind that we have formulated such an assumption because even small displacements may reduce considerably the present foreseen resistance.

The previous relation (5.11) is useful for isolating the associated bending moment M(k) in (5.8). By so doing, we get:
(5.12)
The two previous equations are only valid if because it is impossible to exceed the total plastic capacity of the cross-section. Consequently, according to (5.11), the two mentioned equations may still be used as long as:
(5.13)
If this limit displacement is exceeded in beam k, we simply have and M(k) = 0. Once all internal forces and displacements field are completely defined, the upper-bound theorem is applied for getting the plastic collision resistance of beam k. According to Jones [16], the internal power of a transversal frame may be written as
(5.14)
By introducing (5.10), (5.11), and (5.12) in (5.14), we finally get the individual contribution of beam k to the plastic resistance of the gate in the global deforming mode:
(5.15)

5.5. Total Resistance in Global Deforming Mode

In Sections 5.3 and 5.4, we have established the individual contribution of each transversal frame to the total resistance of the gate. In accordance with (3.12), the total collision force is simply obtained by summation:
(5.16)
where is given by (5.7) if beam k is still in the elastic regime or by (5.16) if plasticity has already occurred. To simplify, the transition between the elastic and the plastic resistance is supposed to happen when the elastic bending moment in section X = XE reaches its maximal value .

6. Combination of Local and Global Deforming Modes

6.1. Resistance of the Beams Already Impacted during the Local Phase

The transition between local and global deforming mode has already been discussed in Section 3.4, where a sudden switch is assumed to occur when δ = δt (the so-called transition value). In the present section, we give more precision on the way to combine two different modes. For a given value of δ, Ploc  is evaluated by (4.5) and Pglob by (5.16). Two cases are then possible.
  • (i)

    If Ploc  > Pglob, then the force applied by the ship on the gate is not sufficient for activating the global deforming mode. Consequently, we have δ < δt and Pt = Ploc , with Ploc  given by (4.5).

  • (ii)

    If Pglob = Ploc , then the global bending mode is activated and the gate starts to resist by an overall movement. So we have δ = δt; the transition value is reached.

For δ ≥ δt, we know that the global mode is valid, but the resistance Pt may no longer be evaluated by relation (5.16). If we examine Figure 26, for example, we see that when the transition occurs at δt, the third transversal frame has already been crushed over a certain length δt − δ0, where δ0 is the initial distance between the bow and the frame. As a consequence, for beam 3, we may not assume that (5.7) and (5.15) are still valid.

It is too conservative to suppose that a beam that has already been crushed during the local phase does not provide any resistance during the global one. On the contrary, the uncrushed part of the cross-section is still able to develop a certain resistance by acting like a membrane. This is illustrated in Figure 25, where, for beam k, we see that the total area of the uncrushed section is
(6.1)
where , , , and are the cross-sectional dimensions for beam k, is the initial distance between the bow and beam k.
Details are in the caption following the image
Figure 25
Open in figure viewerPowerPoint
Resistance in the global mode of a transversal frame already crushed during the local mode.
Details are in the caption following the image
Figure 26
Open in figure viewerPowerPoint
Combination of local and global deforming modes.
When δ > δt − δ0, the internal power developed while producing an additional displacement δ + δ0 − δt of beam k is
(6.2)
where Δ(k) is the axial extension of the transversal frame caused by the displacement δ + δ0 − δt:
(6.3)
Finally, by introducing (6.3) into (6.2), we obtain the resistance of a transversal frame already crushed during the local phase:
(6.4)

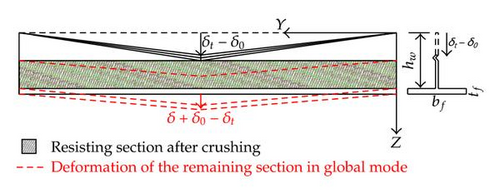
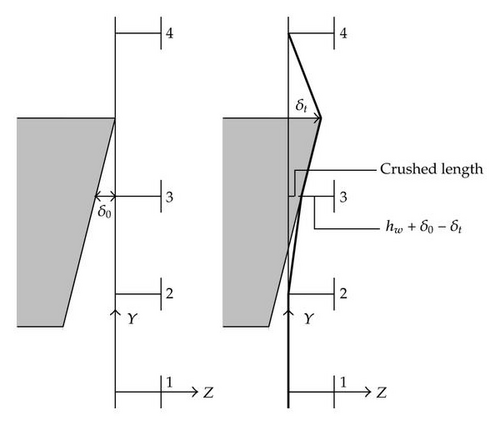
Of course, this formula has only to be applied if , otherwise beam k is not impacted during the local mode and the classic formulae of Section 5 remains valid. However, a correction is still needed to take into account the beginning of a new phase of motion. In fact, in (5.7) and (5.15), we have to evaluate and for the actual global displacement, that is, δ − δt and not for the total displacement δ, which also includes the displacements during the local phase. This concept is illustrated in Figure 27.

Details are in the caption following the image
Figure 27
Open in figure viewerPowerPoint
Total displacement δ and global displacement δ − δt.

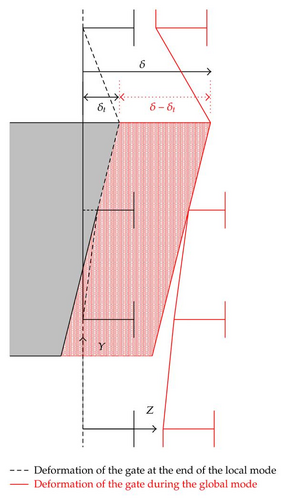
6.2. Total Resistance

In the previous sections, we have established all the required formulas for assessing the resistance in the local and global deforming modes. For clarity, we will now make a short summary of the results.
  • (1)

    At the beginning, the progression of the striking vessel into the gate is allowed by local deformations of the structure. During this local phase, two different forces are evaluated:

    • Ploc (δ)→ see formula (4.5) where is given by

      •    (i) formula (4.2) if superelement k is of type 1,

      •    (ii) formula (4.3) if superelement k is of type 2,

    • Pglob(δ)→ see formula (5.16), where is given by

      •    (i) formula (5.7) if beam k is still in the elastic regime,

      •    (ii) formula (5.15) if beam k is in the plastic regime.

  •  

    During the local phase, the total resistance of the gate Pt is equal to the local one, which means that Pt(δ) = P  (δ).

  •  

    We assume that deformations remain local as long as Pglob(δ) > Ploc (δ). The transition between the local and the global mode occurs at the particular value δt, for which we have Pglob(δt) = Ploc (δt).

  • (2)

    For the values of δ greater than δt, the global mode is activated. The total resistance of the gate is still given by

    (6.5)
    where

    • (i)

      is obtained by formula (5.7) or formula (5.15) if beam k has not been impacted during the local phase; it should be noted that these equations are evaluated in δ − δt and not in δ (see Figure 27),

    • (ii)

      is obtained by formula (6.4) if beam k has been impacted during the local deforming mode,

    • (iii)

      Ploc (δt) is the total resistance of the gate at the end of the local phase.

7. Numerical Validation

In order to validate all the developments described in the previous sections, we compare them to the results obtained by numerical simulations on two different gates. For each studied lock gate, two situations of collision have been considered: in the first case, the impact point E is located in the upper part of the gate; in the second case, it is positioned in the lower part.

7.1. Numerical Model of the Striking Vessel

As mentioned above, we are only interested by the worst damages that may be caused to the gate during the collision. So far, we are not concerned by the destruction of the striking vessel. Therefore, we conservatively assume that the ship is perfectly rigid and will not deform over the total impact duration.

For the numerical simulations, it is useless to deal with the entire ship. We only need to have a quite refined model of the bow. As explained in Section 2, the geometry of the ship is fixed with help of the five parameters p, q, φ, ψ, and hb (see Figure 28). Its mass M0 is noted and its initial velocity V0. For the present example, we have chosen the numerical values listed in Table 1. These parameters have been chosen in order to represent a classical ship for the inland waterways.

Table 1. Numerical data describing the striking vessel.
p q φ ψ hb M0 V0
6 m 8 m 84° 84° 5 m 4000 t 2 m/s
Details are in the caption following the image
Figure 28
Open in figure viewerPowerPoint
Numerical model of the striking vessel.

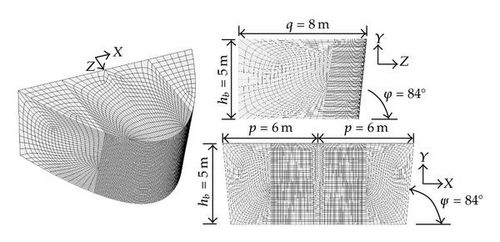
The numerical model of the vessel is shown in Figure 28. It is composed of 6955 Belytschko-Tsai shell elements, which are described in the LS-DYNA theoretical manual by Hallquist [17]. As it can be seen in Figure 28, the mesh is more refined in the central zone of the ship, where the contact with the gate is likely to occur. In this region, the mesh size is about 1 cm × 1 cm. In the remaining parts of the model, as they are not supposed to develop any contact with the impacted structure, the mesh is coarser.

The material used for modeling the bow is assumed to be rigid. It is defined with help of the classical properties of steel recalled in Table 2. These parameters are only required for defining the contact conditions between the ship and the gate. They are not used for calculating any deformation in the vessel, as the material is infinitely rigid.

Table 2. Useful properties for defining a rigid material law (only required for contact simulation).
Property Notation Value
Density ρ 7850 kg/m3
Young’s modulus EY 210 000 MPa
Poisson’s ratio ν 0.33

7.2. Numerical Model of Gate 1

The main dimensions of the structure are plotted in Figure 29. The total height and length of the gate are H = 13.1 m and L = 13.1 m. The stiffening system of the structure is made of
  • (i)

    five transversal frames, which are irregularly distributed over the height H of the gate; their vertical positions along the vertical Y axis are shown in Figure 29(b);

  • (ii)

    six vertical frames, which are regularly placed over the length L of the gate; their locations along the transversal X axis are plotted in Figure 29(c);

  • (iii)

    twenty stiffeners distributed over the height H of the gate with an average space of 66 cm.

Details are in the caption following the image
Figure 29 (a)
Open in figure viewerPowerPoint
Numerical model of gate 1.
Details are in the caption following the image
Figure 29 (b)
Open in figure viewerPowerPoint
Numerical model of gate 1.
Details are in the caption following the image
Figure 29 (c)
Open in figure viewerPowerPoint
Numerical model of gate 1.

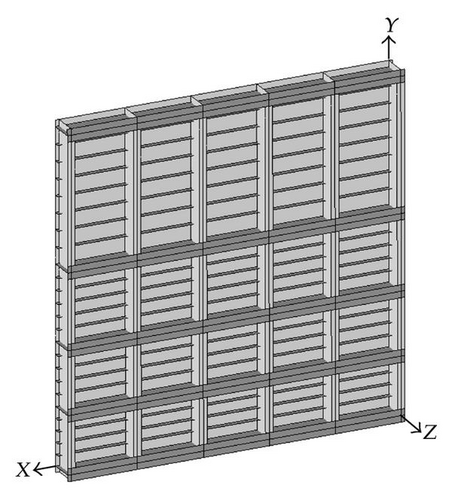
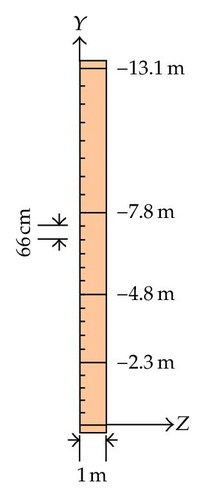
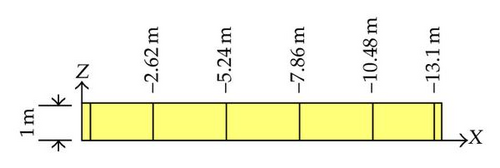
Other geometrical data are listed in Table 3. The corresponding notations are defined in accordance with the symbols introduced in Figure 3. Note that the transversal and vertical frames have a T-shaped cross-section, while the stiffeners simply have a rectangular one. The gate is modeled with help of 204226 Belytschko-Tsai shell elements. The mesh is quite refined, with a mesh size of 5 cm × 5 cm. Of course, it may appear excessive to use such a regular mesh over the entire structure, but it was required because we did not know in advance which part of the gate would be impacted by the ship. In order to avoid contact problems, this solution has been chosen.

Table 3. Geometrical data defining gate 1.
Element Property Notation Value (mm)
Plating Thickness tp 10
Transversal frames Web thickness tw 22
Web height hw 1000
Flange thickness tf 22
Flange width bf 300
Vertical frames Web thickness tw 22
Web height hw 1000
Flange thickness tf 22
Flange width bf 500
Stiffeners Web thickness tw 10
Web height hw 200
Flange thickness tf 0
Flange width bf 0

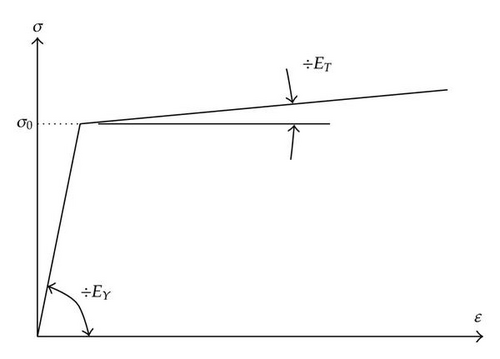
The material used for gate 1 is defined to represent more or less the behaviour of steel. The elastic-plastic stress-strain curve may be divided in two distinct portions (see Figure 30). The first part of the curve corresponds to the elastic phase. The stress-strain curve is linear, with an inclination corresponding to Young’s Modulus EY. When the yield stress σ0 is reached, the plastic phase begins. The stress-strain curve is still linear, but the slope has changed and is given by the tangent modulus ET. In the present low velocity impact model, the strain-rate effect is not taken into account. The values of the different parameters are listed in Table 4.

Table 4. Useful properties for defining the material law of steel.
Property Notation Value
Density ρ 7850 kg/m3
Poisson’s ratio ν 0.33
Yield stress σ0 240 MPa
Young’s modulus EY 210 000 MPa
Tangent modulus ET 1018 MPa
Details are in the caption following the image
Figure 30
Open in figure viewerPowerPoint
Stress-strain relation of steel.

The support conditions are the ones described in Section 2, that is, displacements in direction Z are blocked in X = 0, X = L, and Y = 0.

7.3. Numerical Model of Gate 2

The second gate is wider than the first one. Its total height and length are H = 15 m and L = 17.1 m. The main dimensions are plotted in Figure 31. (Please note that the origin of the axes (X, Y, Z) is correctly positioned, regarding all the previous figures.) This time, the stiffening system is more compact and made of
  • (i)

    five transversal frames, whose vertical positions along the Y axis are shown on Figure 31;

  • (ii)

    six vertical frames, regularly separated by a distance of 1.9 m;

  • (iii)

    twenty-six stiffeners, regularly separated by a distance of 50 cm.

Details are in the caption following the image
Figure 31 (a)
Open in figure viewerPowerPoint
Numerical model of gate 2.
Details are in the caption following the image
Figure 31 (b)
Open in figure viewerPowerPoint
Numerical model of gate 2.
Details are in the caption following the image
Figure 31 (c)
Open in figure viewerPowerPoint
Numerical model of gate 2.

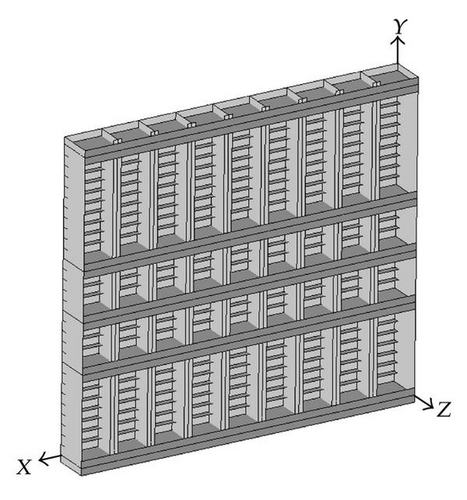
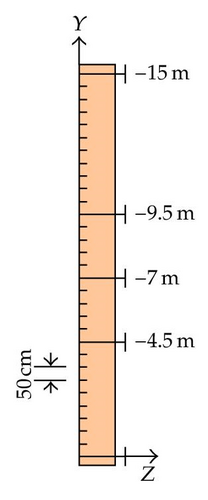
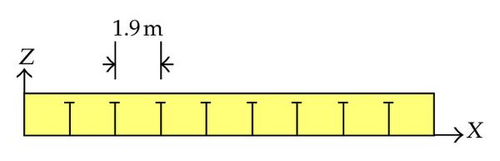
Other geometrical data are listed in Table 6. The gate is modeled by 92671 Belytschko-Tsai shell elements. The regular mesh size is 10 cm × 10 cm. The material model and the support conditions are the same as for gate 1.

7.4. Numerical Simulations

Four numerical simulations have been performed by using the finite-elements software LS-DYNA. Two simulations are required for each gate, according to the position of the impact point E. The transversal and vertical positions XE and YE of point E are listed in Table 5 for the different collision cases considered here.

Table 5. Impact location for the simulations.
Simulation 1 Simulation 2
Gate 1 XE = 6.55 m XE = 6.55 m
YE = 8 m YE = 13.1 m
  
Gate 2 XE = 8.55 m XE = 8.55 m
YE = 7.5 m YE = 13.25 m
Table 6. Geometrical date defining gate 2.
Element Property Notation Value (mm)
Plating Thickness tp 12
Transversal frames Web thickness tw 12
Web height hw 1800
Flange thickness tf 12
Flange width bf 400
Vertical frames Web thickness tw 12
Web height hw 1400
Flange thickness tf 12
Flange width bf 300
Stiffeners Web thickness tw 12
Web height hw 300
Flange thickness tf 0
Flange width bf 0

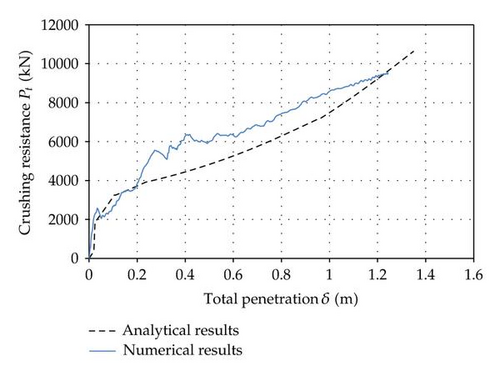
Concerning the resulting crushing force curves compared in Figures 32 and 33, simulation 1 corresponds to a ship impact happening in the lower part of the structure and simulation 2 to an impact in the upper one.

Details are in the caption following the image
Figure 32 (a)
Open in figure viewerPowerPoint
Comparison of the analytical and numerical crushing forces for gate 1.
Details are in the caption following the image
Figure 32 (b)
Open in figure viewerPowerPoint
Comparison of the analytical and numerical crushing forces for gate 1.
Details are in the caption following the image
Figure 33 (a)
Open in figure viewerPowerPoint
Comparison of the analytical and numerical crushing forces for gate 2.
Details are in the caption following the image
Figure 33 (b)
Open in figure viewerPowerPoint
Comparison of the analytical and numerical crushing forces for gate 2.

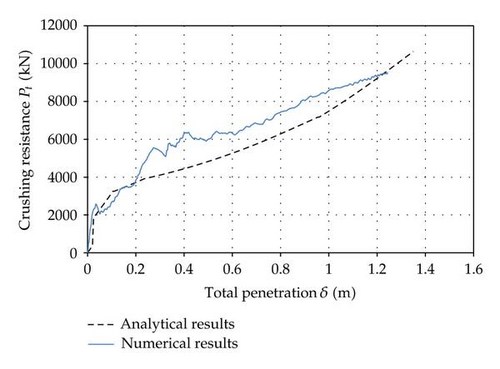
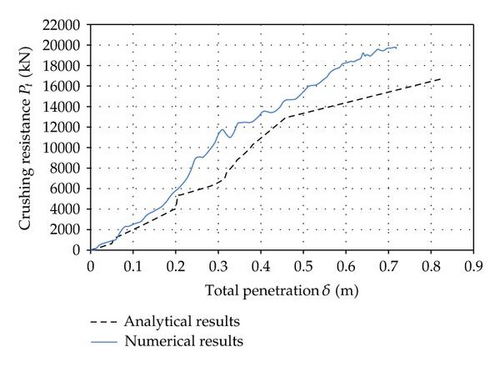
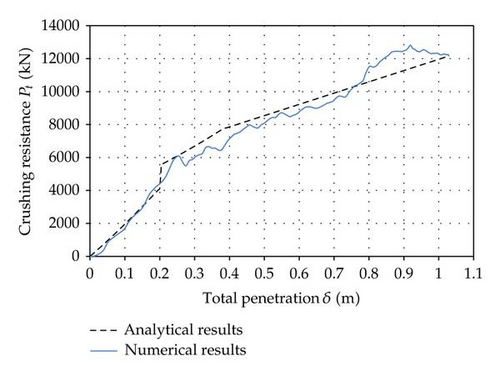
7.5. Comparison of Numerical and Analytical Results

In order to validate the analytical developments established in the previous section, we will make a comparison between the results provided by LS-DYNA and the ones predicted by our simplified method. The curves of interest are those showing the evolution of the crushing force Pt with the total penetration δ. The comparisons are plotted in Figures 32 and 33. The curves referenced as “numerical results” are those obtained by LS-DYNA, while the “analytical results” are derived by the present simplified approach.

As it can be seen, the agreement between the curves is quite good. In most cases, the analytical curves provide slightly conservative results. However, for gate 2, the first simulation (see Figure 33(a)) exhibits a more important divergence: our simplified method tends to underestimate the crushing resistance, especially for the great values of δ. This observation is due to a quite conservative approach in the global mode. This may be explained by the two following reasons.
  • (i)

    The resisting cross-sections are determined according to the recommendations of Eurocode 3. It seems that these rules are quite severe in the present case as the numerical simulations show that a greater part of the plating is actually collaborating to the resistance of the transversal frames.

  • (ii)

    We do not capture properly the deformation pattern of the vertical frames: we suppose that their role is limited to the application of the global displacements field, but we neglect the energy also dissipated through their own global deflection.

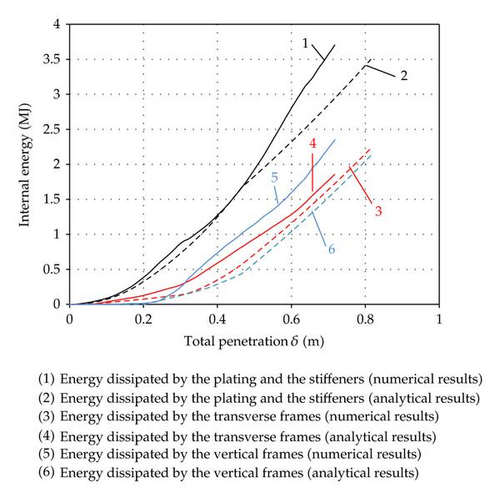
This last point is confirmed by the curves plotted on Figure 34, where we compare the energy dissipated by the different structural components of the gate. The numerical results are those given by LS-DYNA, while the analytical results are those predicted by the theoretical model of this paper. As it can be seen on this picture, the discrepancy is satisfactory for the plating, the stiffeners, and the transverse frames, but it is not really the case for the vertical frames. Our method underestimates the energy that these elements really dissipate, but this approximation remains conservative.

Details are in the caption following the image
Figure 34
Open in figure viewerPowerPoint
Comparison of the analytical and numerical internal energy of the various components of the gate.

8. Conclusion

In this paper, we exposed a simplified procedure for assessing the resistance of a gate submitted to a ship impact.

It is important to bear in mind the hypotheses that we have formulated for modeling the struck gate and the striking vessel. Concerning the struck gate, our approach is devoted to
  • (i)

    gates with single plating; structures with double plating or caissons are not covered by the present developments;

  • (ii)

    gates with a classical orthogonal stiffening system, that is, stiffeners and frames in the transversal direction and frames in the vertical direction;

  • (iii)

    gates supported on both sides by the lock walls and by a sill at the bottom of the lock.

The three former conditions have to be fulfilled for applying the methodology exposed previously. Concerning the striking vessel, it is modeled by using a certain number of parameters. The global bow shape is assumed to be a parabola, with given radii p and q, decreasing according to given stem and side angles φ and ψ.

The impacted structure is assumed to behave in two phases. At the beginning, when the indentation δ of the ship is not too wide, we suppose a localized crushing of some impacted structural elements. The plating and the stiffening system surrounding the initial contact zone are submitted to heavy deformations, but the remaining of the gate is still unaffected. In this case, we say that the structure withstands through a local deforming mode. For such a situation, the resistance is calculated by summing all the contributions of the activated superelements. As some references are already available in the literature, we have not reproduced all the developments concerning these superelements.

When the penetration δ becomes wider, the gate withstands through an overall movement implying the entire structure. In this case, we say that the resistance is provided through a global deforming mode. For the support conditions assumed presently, the required theoretical displacements fields have been exposed in detail. We also derived an equivalent mechanical model for evaluating the resistance in such a situation.

The transition between the local and the global deforming modes is assumed to occur at a given penetration δt, for which the collision force exerted by the ship during the local phase is sufficient to produce an overall displacement of the gate.

Finally, our presentation ends with a comparison between some finite elements numerical results and those obtained by the present simplified approach. In most cases, the procedure exposed here leads to a quite satisfactory estimation of the collision resistance. The predicted results are conservative, without underestimating too much the numerical values.

The main advantage of the methodology exposed here is to provide rapidly an evaluation of the collision resistance. The analytical curves plotted in Figures 32 and 33 are useful for knowing if a lock gate is able to behave satisfactorily to an impact of a ship with given initial velocity V0 and mass M0. With these curves, it is in fact possible to know the total needed indentation δmax  required for dissipating the initial kinetic energy . If this value of δmax  exceeds a given criterion, then we may suppose that the structure will not be able to withstand satisfactorily a collision with a vessel of mass M0 and velocity V0.

Of course, we have to be conscious that our simplified analytical method is only applicable at the predesign stage of a lock. For more advanced stages of a project, it is still necessary to resort to more advanced tools, like finite elements software.

List of Notations: Lower-Case Latin Notations

  • a1:
  • Horizontal or vertical dimension of a superelement defined by the impact point location and the supports of the struck structure
  • a2:
  • Horizontal or vertical dimension of a superelement defined by the impact point location and the supports of the struck structure (complementary to a1)
  • b1:
  • Vertical dimension of a superelement defined by the impact point location and the supports of the struck structure
  • b2:
  • Vertical dimension of a superelement defined by the impact point location and the supports of the struck structure (complementary to a2)
  • beff:
  • Effective width for calculating the section properties of a transversal beam
  • bf:
  • Flange width of a stiffener or a transversal frame
  • hb:
  • Vertical distance between the lowermost and uppermost decks of the striking ship
  • hp:
  • Collaborating width of the plating in the global deforming mode
  • hw:
  • Web height of a stiffener or a transversal frame
  • k:
  • Superscript used for referencing a particular property of superelement n°k
  • n:
  • Total number of superelements used for modeling the entire gate
  • (p, q):
  • Parameters defining the parabolic dimensions of the striking ship uppermost deck
  • tf:
  • Flange thickness of a stiffener or a transversal beam
  • tp:
  • Thickness of the plating
  • tw:
  • Web thickness of stiffener or a transversal frame
  • tX:
  • Equivalent plating thickness after smearing all the transversal stiffeners
  • tY:
  • Equivalent plating thickness after smearing all the vertical stiffeners.

    • Upper-Case Latin Notations

  • E:
  • Young’s modulus of the steel material constituting the gate
  • Eext:
  • External energy
  • Eint 
  • Internal energy
  • ET:
  • Tangent modulus of steel
  • EY:
  • Young’s modulus of steel
  • H:
  • Total vertical height of the gate
  • I:
  • Bending inertia of a transversal beam
  • L:
  • Total transversal length of the gate
  • M:
  • Bending moment
  • Mp:
  • Plastic bending resistance of a transversal beam
  • M0:
  • Mass of the striking ship
  • N:
  • Axial force
  • Np:
  • Plastic axial resistance of a transversal beam
  • Pglob:
  • Total resistance of the gate in the global deforming mode
  • Ploc :
  • Total resistance of the gate in the local deforming mode
  • Pt:
  • Total collision resistance of the impacted gate
  • W(X, δ):
  • Transversal evolution of the displacement field in the global deforming mode
  • WE(Y, δ):
  • Vertical evolution of the displacement field in the global deforming mode
  • (XE, YE):
  • Impact point location on the gate
  • (X, Y, Z):
  • General coordinate system.

    • Lower-Case Greek Notations

  • δ:
  • Penetration of the striking ship
  • δc:
  • Penetration of the striking ship for which a second contact between the gate and the bow is established
  • δt:
  • Penetration of the striking ship at the transition between the local and the global deforming modes
  • δmax :
  • Maximal penetration of the striking ship required for completely dissipating its initial kinetic energy
  • δ0:
  • Initial distance between the bow and a transversal beam
  • ϵu:
  • Deformation for which the ultimate stress σu is reached
  • ϵ0:
  • Deformation for which the plastic limit σ0 is reached
  • ϵij:
  • Strain tensor
  • θ:
  • Cross-section rotation
  • ν:
  • Poisson’s ratio of steel
  • ρ:
  • Mass density of steel
  • σu:
  • Ultimate stress of steel
  • σ0:
  • Plastic limit of steel
  • σij:
  • Stress tensor
  • ϕ:
  • Stem angle
  • χ:
  • Curvature of a transversal beam
  • ψ:
  • Side angle.

    • Upper-Case Greek Notations

  • Γ:
  • Designation of the parabola describing the striking ship uppermost deck
  • Δ:
  • Total axial extension of transversal frame.

      • The full text of this article hosted at iucr.org is unavailable due to technical difficulties.