Volume 2012, Issue 1 752950

Research Article

Open Access

On Stochastic Finite-Time Control of Discrete-Time Fuzzy Systems with Packet Dropout

Yingqi Zhang,

Yingqi Zhang

College of Science, Henan University of Technology, Zhengzhou 450001, China admissions.cn

Search for more papers by this author

Caixia Liu,

Caixia Liu

College of Science, Henan University of Technology, Zhengzhou 450001, China admissions.cn

Search for more papers by this author

Xiaowu Mu,

Corresponding Author

Xiaowu Mu

[email protected]

Department of Mathematics, Zhengzhou University, Zhengzhou 450001, China zzu.edu.cn

Search for more papers by this author

Yingqi Zhang,

Yingqi Zhang

College of Science, Henan University of Technology, Zhengzhou 450001, China admissions.cn

Search for more papers by this author

Caixia Liu,

Caixia Liu

College of Science, Henan University of Technology, Zhengzhou 450001, China admissions.cn

Search for more papers by this author

Xiaowu Mu,

Corresponding Author

Xiaowu Mu

[email protected]

Department of Mathematics, Zhengzhou University, Zhengzhou 450001, China zzu.edu.cn

Search for more papers by this author

First published: 01 February 2012

https://doi.org/10.1155/2012/752950

Citations: 9

Academic Editor: M. De la Sen

Share a link

Email
Wechat
Bluesky

Abstract

This paper is concerned with the stochastic finite-time stability and stochastic finite-time boundedness problems for one family of fuzzy discrete-time systems over networks with packet dropout, parametric uncertainties, and time-varying norm-bounded disturbance. Firstly, we present the dynamic model description studied, in which the discrete-time fuzzy T-S systems with packet loss can be described by one class of fuzzy Markovian jump systems. Then, the concepts of stochastic finite-time stability and stochastic finite-time boundedness and problem formulation are given. Based on Lyapunov function approach, sufficient conditions on stochastic finite-time stability and stochastic finite-time boundedness are established for the resulting closed-loop fuzzy discrete-time system with Markovian jumps, and state-feedback controllers are designed to ensure stochastic finite-time stability and stochastic finite-time boundedness of the class of fuzzy systems. The stochastic finite-time stability and stochastic finite-time boundedness criteria can be tackled in the form of linear matrix inequalities with a fixed parameter. As an auxiliary result, we also give sufficient conditions on the stochastic stability of the class of fuzzy T-S systems with packet loss. Finally, two illustrative examples are presented to show the validity of the developed methodology.

1. Introduction

Systems where feedback loops are closed via digital communication channel are often regarded as networked control systems (NCSs). Compared with traditional point-to-point controller architectures, the advantages of NCSs include low cost, easy maintenance, and increased system flexibility, and so on. However, the insertion of the communication channels creates discrepancies between the data records to be transmitted and their associated remotely transmitted images and hence raises new interesting problems such as quantization, time delays, and data packet loss, see the references [1–4] and the references cited therein. Among a number of issues arising from such a framework, packet loss of NCSs is an important issue to be addressed and has been receiving great attentions. For instance, Xiong and Lam [5] studied the problem of stability and stabilization of linear systems over networks with bounded packet loss. Bakule and De La Sen [6] tackled the problem of decentralized stabilization of networked complex composite systems with nonlinear perturbations. Wang and Yang [7] investigated the problem of state-feedback control synthesis for networked control systems with packet dropout. For more details of the literature related to networked problems with packet dropout, the reader is referred to [8–16] and the references therein. It is worth noting that Takagi-Sugeno (T-S) fuzzy model has been recognized as a popular and powerful tool in approximating and describing complex nonlinear systems [17] in the sense that it can be able to achieve any degree of accuracy in any convex compact set. The T-S fuzzy model is appealing since it combines the flexible fuzzy logic theory and fruitful linear multivariable system theory into a unified framework and then carries out the control design and analysis via Lyapunov function-based approaches. By choosing appropriate Lyapunov functions including a common Lyapunov function, piecewise Lyapunov function, or fuzzy (nonquadratic) Lyapunov function, the stability and stabilization of the class of fuzzy systems can be determined by solving a set of linear matrix inequalities (LMIs), for instance, see [18–24] and the references cited therein.

It is worth pointing out that classical control theory focuses mainly on the asymptotic behavior of the systems, which, just as was mentioned above, deals with the asymptotic property of system trajectories over an infinite time interval and does not usually specify bounds on the trajectories. In many practical applications, however, many concerned problems are the practical ones which described system state that does not exceed some bound during some time interval, for example, large values of the state are not acceptable in the presence of saturations [25]. In order to deal with these transient performance of control systems, finite-time stability or short-time stability was presented in [26]. Applying linear matrix inequality theory, some appealing results were obtained to ensure finite-time stability, finite-time boundedness, and finite-time stabilization of various systems including linear systems, nonlinear systems, fuzzy systems, and stochastic systems. For instance, Zhang and An [27] addressed the problem of finite-time stability and stabilization of linear stochastic systems. Ambrosino et al. [28] investigated finite-time stability of impulsive dynamic systems. For more details of the literature related to finite-time stability, the reader is referred to [29–35], and the references therein. However, to date and to the best of our knowledge, the problems of stochastic finite-time stability and stabilization of fuzzy systems with packet loss have not been investigated, although results related to fuzzy control systems over networks with packet loss are available in the existing literature, see the references [14–16], which motivates the main purpose of our study.

In this paper, we tackle the stochastic finite-time stability (SFTS) and stochastic finite-time boundedness (SFTB) problems for one family of fuzzy discrete-time systems over networks with packet dropout, parametric uncertainties, and time-varying norm-bounded disturbance. Firstly, we present dynamic model description studied, which, if the data packet loss is assumed to be a time-homogenous Markov process, the discrete-time fuzzy T-S systems with packet loss can be regarded as one class of fuzzy Markovian jump systems. Markov jump systems are referred to as a special family of hybrid systems and stochastic systems, which are very appropriate to model plants whose structure is subject to random abrupt changes, see the papers [36–41]. Thus, the class of fuzzy systems studied can be disposed by the theoretical framework of Markov jumps systems. Then, the concepts of SFTS and SFTB and problem formulation are given. The main contribution of this paper is to design a state-feedback controller which guarantees the resulting closed-loop fuzzy discrete-time system with Markovian jumps SFTS and SFTB. The SFTS and SFTB criteria can be tackled in the form of LMIs with a fixed parameter. As an auxiliary result, sufficient conditions on the stochastic stability of the class of fuzzy T-S systems with packet loss are also presented.

The rest of this paper is organized as follows. Section 2 devotes to the dynamic model description and problem formulation. The results on the SFTS and SFTB are given in Section 3. Section 4 presents numerical examples to demonstrate the validity of the proposed methodology. In Section 5, some conclusions are drawn.

Notations 1. The notation used throughout the paper is fairly standard, ℝⁿ, ℝ^n×m, and ℤ⁺ denoting the sets of n component real vectors, n × m real matrices, and the set of nonnegative integers, respectively. The superscript T stands for matrix transposition or vector and 𝔼{·} denotes the expectation operator with respect to some probability measure ℙ. In addition, the symbol * denotes the transposed elements in the symmetric positions of a matrix. λ_min(P) and λ_max(P) denote the smallest and the largest eigenvalue of matrix P, respectively. Notations sup and inf denote the supremum and infimum, respectively. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operations.

2. Problem Formulation and Preliminaries

2.1. Physical Plant

The fuzzy model proposed by Takagi and Sugeno [17] is described by fuzzy IF-THEN rules, which represents local near input-output relations of a nonlinear system. The rules of the T-S fuzzy models are of the following forms, here DFS denotes the the discrete-time fuzzy system.

Fuzzy Rule i IF θ₁(k) is M_i1 and θ₂(k) is M_i2 ⋯ θ_c(k) is M_ic, THEN

(2.1)

where i ∈ 𝕄∶ = {1,2, …, r}, x(k) ∈ ℝⁿ is the state, u(k) ∈ ℝ^m is the control input, r is the number of IF-THEN rule, M_i1, M_i2, …, M_ic are fuzzy variable, and θ(k) = [θ₁(k), θ₂(k), …, θ_c(k)] is the premise variables vector. It is assumed the premise variable does not depend on the input variable u(k), which is employed to avoid a complicated defuzzification process of fuzzy controllers [22]. The noise signal w(k) ∈ ℝ^l satisfies

(2.2)

The matrices ΔA_i(k), ΔB_i(k), and ΔG_i(k) are uncertain matrices and satisfy

(2.3)

where Δ_i(k) is an unknown, time-varying matrix function and satisfies

(2.4)

Given a pair of (x(k), u(k)), the final outputs of the fuzzy systems are inferred as follows:

(2.5)

where h_i(θ(k)) are fuzzy basis function given by

(2.6)

where M_ij(θ_j(k)) represents the grade of membership of θ_j(k) in M_ij. Then, it can be seen that

(2.7)

Therefore, we can obtain

(2.8)

2.2. Communication Links and Controller

Owing to the existence of the packet dropout of the communication during the transmission, the packet dropout process of the network can be regarded as a time-homogenous Markov process {γ(k), k ≥ 0}. Let γ(k) = 1 mean that the packet has been successfully delivered to the decoder while γ(k) = 0 corresponds to the dropout of the packet. The Markov chain has a transition probability matrix defined by

(2.9)

where i, j ∈ 𝕎 : = {0,1} are the state of the Markov chain. Without loss of generality, let γ(0) = 1 and the failure rate p and the recovery rate q of the channel satisfy p, q ∈ (0,1). It is worth noting that a smaller value of p and a larger value of q indicate a more reliable channel.

Remark 2.1. When the above transition probability matrix is with 0 ≤ p ≤ 1, the above two-state Markov process is reduced to a Bernoulli process [42].

In this paper, we consider the following fuzzy control law for the DFS (2.5).

Controller Rule i IF θ₁(k) is M_i1 and θ₂(k) is M_i2 ⋯ θ_c(k) is M_ic, THEN

(2.10)

where L_i are to be designed the control gain matrices. {γ(k), k ≥ 0} is a Markov packet dropout process satisfying (2.9). Then, we have the controller of DFS as

(2.11)

2.3. Closed-Loop System

The following closed-loop DFS can be obtained from (2.5) and (2.11):

(2.12)

where

, and

Now, we define two models according to the value of γ(k). If γ(k) = 1, we define the Model 1 at time k + 1 as follows:

(2.13)

If γ(k) = 0, we define the Model 2 at time k + 1 as follows:

(2.14)

where the selection of L_jζ in (2.13) is according to the model of x(k) for all ζ ∈ {1,0}, that is to say, if x(k) is at Model 1, which is γ(k − 1) = 1, L_jζ = L_j1, otherwise, if x(k) is at Model 2, which is γ(k − 1) = 0, L_jζ = L_j0.

Then, (2.12) can be regarded as a DFS with Markovian jumps described by

(2.15)

where 1(a), a ∈ {1,2} denotes the mode indicator function. 1(1) corresponds to a mode with feedback and 1(2) corresponds to a mode without feedback. It is noted that it yields 1(a) = 1 when at time k + 1 be a ∈ {1,2} and 1(b) = 0 for b ≠ a. The mode transition probabilities of Markovian jump DFS (2.15) is given by

(2.16)

where π_uv ≥ 0 for all u, v ∈ {1,2} and

. η_v(k) = 1 implies 1(1) = 1, 1(2) = 0, which the communication transmission succeeds, and η_v(k) = 2 implies 1(1) = 0, 1(2) = 1, in which the communication dropout occurs. Thus, compared with (2.9), it follows that π₁₁ = 1 − p, π₁₂ = p, π₂₁ = q, π₂₂ = 1 − q.

2.4. Definitions and Lemmas

Definition 2.2 (stochastic finite-time stability (SFTS)). The closed-loop DFS with Markov jumps (2.15) with w(k) = 0 is said to be SFTS with respect to (δ_x, ϵ, R, N), where 0 < δ_x < ϵ, R is a symmetric positive-definite matrix, and N ∈ ℤ⁺, if

(2.17)

Definition 2.3 (stochastic finite-time bounded (SFTB)). The closed-loop DFS with Markov jumps (2.15) is said to be SFTB with respect to (δ_x, ϵ, R, N, d), where 0 < δ_x < ϵ, R is a symmetric positive-definite matrix, and N ∈ ℤ⁺, if

(2.18)

Lemma 2.4 (see [23].)For any matrices M_ij, N_ij for 1 ≤ i, j ≤ r, and S > 0 with appropriate dimensions, one has

(2.19)

In particular, when M_ij = N_ij for all 1 ≤ i, j ≤ r, one has

(2.20)

Lemma 2.5 (Schur complement lemma, see [43]). The linear matrix inequality is equivalent to X₂₂ < 0 and , where and .

Lemma 2.6 (see [43].)For matrices X, Y and Z of appropriate dimensions, where X is a symmetric matrix, then

(2.21)

holds for all matrix F(t) satisfying F^T(t)F(t) ≤ I for all t ∈ ℝ, if and only if there exists a positive constant κ, such that the following inequality holds:

(2.22)

In this paper, the feedback gain matrices L_j1 and L_j0 with Markov packet dropout of failure rate p and recovery rate q will be designed to guarantee the states of the closed-loop Markovian jump DFS (2.15) SFTB and SFTS.

3. Main Results

In this section, for the given failure rate p and recovery rate q with p, q ∈ (0,1), we start by developing results that can be used to design a state-feedback controller that assures that the nominal Markovian jump DFS (2.15) is SFTB and SFTS. Then, these results will be extended to the case of uncertain systems. LMI conditions are established to design a state-feedback controller that guarantees that either a nominal Markovian jump DFS or an uncertain Markovian jump DFS of the class we are considering is SFTB and SFTS.

3.1. SFTB and SFTS of the Nominal Markov Jump System

Theorem 3.1. For the given failure rate p and recovery rate q with p, q ∈ (0,1), the closed-loop nominal Markovian jump DFS (2.15) is SFTB with respect to (δ_x, ϵ, R, N, d), if there exist a scalar μ ≥ 1, four symmetric positive-definite matrices P₁, P₂, Q₁, Q₂, and a set of feedback control matrices {L_jζ, j ∈ 𝕄, ζ ∈ {1,0}}, such that the following inequalities hold for all i, j ∈ 𝕊:

(3.1)

(3.2)

(3.3)

where

for all a ∈ {1,2}.

Proof. Assume the mode at time k be a ∈ {1,2}. Taking into account that if a = 1, then we have γ(k − 1) = 1 and L_jζ = L_j1, otherwise, if a = 2, then γ(k − 1) = 0 and L_jζ = L_j0. Let us consider the following quadratic Lyapunov-Krasovskii functional candidate for the Markov jump DFS (2.15):

(3.4)

We compute

(3.5)

According to Lemma 2.4, we obtain

(3.6)

where

(3.7)

Taking into account that if a = 1, then L_jζ = L_j1, otherwise, a = 2, then L_jζ = L_j0. Noting that π₁₁ = 1 − p, π₁₂ = p, π₂₁ = q, π₂₂ = 1 − q. Thus, when a = 1, we have

(3.8)

where

(3.9)

By Lemma 2.5, we can obtain from (3.1) that

(3.10)

Thus, when a = 1, from (3.6)–(3.10), we can obtain

(3.11)

When a = 2, taking into account condition (3.2), the similar as the above discussion, we can obtain the following inequality:

(3.12)

Thus, for all a ∈ {1,2}, it follows from (3.11) and (3.12) that

(3.13)

By (3.13), it is obvious that

(3.14)

From (2.2) and (3.14) and noting that μ ≥ 1, we have

(3.15)

Let

and noting that

, we have

(3.16)

On the other hand, for all a ∈ {1,2}, we have

(3.17)

Combine (3.15)–(3.17) together, we can obtain

(3.18)

Noting condition (3.3), it follows that 𝔼{x^T(k)Rx(k)} < ϵ² for all k ∈ {1,2, …, N}. This completes the proof of this Theorem.

The similar proof is as the above Theorem 3.1, if w(k) = 0, we can obtain the results on finite-time stability as follows.

Corollary 3.2. For the given failure rate p and recovery rate q with p, q ∈ (0,1), the closed-loop nominal Markovian jump DFS (2.15) with w(k) = 0 is SFTS with respect to (δ_x, ϵ, R, N), if there exist a scalar μ ≥ 1, two symmetric positive-definite matrices P₁, P₂, and a set of feedback control matrices {L_jζ, j ∈ 𝕄, ζ ∈ {1,0}}, such that the following inequalities hold for all i, j ∈ 𝕊:

(3.19)

where

for all a ∈ {1,2}.

Remark 3.3. If μ = 1 is a solution of feasibility problem (3.19), then the closed-loop Markovian jumps DFS (2.15) with w(t) = 0 is SFTS with respect to (δ_x, ϵ, R, N) and is also stochastically stable.

Denoting , one can obtain the following results on the stochastic finite-time stabilization.

Theorem 3.4. For the given failure rate p and recovery rate q with p, q ∈ (0,1), there exists a state-feedback controller u(t) = L_jζx(t), ζ ∈ {1,0} with such that the closed-loop nominal DFS with Markovian jump (2.15) is SFTB with respect to (δ_x, ϵ, R, N, d), if there exist a scalar μ ≥ 1, four symmetric positive-definite matrices X₁, X₂, Q₁, Q₂, and a set of feedback control matrices {Y_jζ, j ∈ 𝕄, ζ ∈ {1,0}}, such that the following inequalities hold for all i, j ∈ 𝕊:

(3.20)

(3.21)

(3.22)

where

for all a ∈ {1,2}.

Corollary 3.5. For the given failure rate p and recovery rate q with p, q ∈ (0,1), there exists a state-feedback controller u(t) = L_jζx(t), ζ ∈ {1,0} with such that the closed-loop nominal Markovian jump DFS (2.15) with w(k) = 0 is SFTS with respect to (δ_x, ϵ, R, N), if there exist a scalar μ ≥ 1, two symmetric positive-definite matrices X₁, X₂, and a set of feedback control matrices {Y_jζ, j ∈ 𝕄, ζ ∈ {0,1}}, such that the following inequalities hold for all i, j ∈ 𝕊:

(3.23)

(3.24)

(3.25)

where

for all a ∈ {1,2}.

3.2. Extension to SFTB and SFTS of the Uncertain Markov Jump DFS

By Theorems 3.1 and 3.4 and applying Lemmas 2.5 and 2.6, one can obtain the following results stated.

Theorem 3.6. For the given failure rate p and recovery rate q with p, q ∈ (0,1), there exists a state-feedback controller u(t) = L_jζx(t), ζ ∈ {1,0} with such that the closed-loop uncertain DFS with Markovian jump (2.15) is SFTB with respect to (δ_x, ϵ, R, N, d), if there exist a scalar μ ≥ 1, two sets of positive scalars {ϵ_1i, i ∈ 𝕄}, {ϵ_2i, i ∈ 𝕄}, four symmetric positive-definite matrices X₁, X₂, Q₁, Q₂, and a set of feedback control matrices {Y_jζ, j ∈ 𝕄, ζ ∈ {1,0}}, such that (3.22) and the following inequalities hold for all i, j ∈ 𝕊:

(3.26)

(3.27)

where

for all a ∈ {1,2}.

Corollary 3.7. For the given failure rate p and recovery rate q with p, q ∈ (0,1), there exists a state-feedback controller u(t) = L_jζx(t), ζ ∈ {1,0} with such that the closed-loop uncertain DFS with Markovian jump (2.15) with w(k) = 0 is SFTS with respect to (δ_x, ϵ, R, N), if there exist a scalar μ ≥ 1, two sets of positive scalars {ϵ_1i, i ∈ 𝕄}, {ϵ_2i, i ∈ 𝕄}, two symmetric positive-definite matrices X₁, X₂, and a set of feedback control matrices {Y_jζ, j ∈ 𝕄, ζ ∈ {0,1}}, such that (3.25) and the following inequalities hold for all i, j ∈ 𝕊:

(3.28)

(3.29)

where

for all a ∈ {1,2}.

Remark 3.8. It is easy to check that conditions (3.22) and (3.25) are guaranteed by imposing the conditions for all a ∈ {1,2}, respectively:

(3.30)

(3.31)

Conditions (3.26)–(3.31) are not strict LMIs, however, once we fix the parameter μ, the conditions can be turned into LMIs based feasibility problem.

Remark 3.9. From the above discussion, we can obtain that the feasibility of conditions stated in Theorem 3.6 and Corollary 3.7 can be turned into the following LMIs based feasibility problem with a fixed parameter μ, respectively:

(3.32)

Furthermore, we can also find the parameter μ by an unconstrained nonlinear optimization approach, in which a locally convergent solution can be obtained by using the program fminsearch in the optimization toolbox of MATLAB.

4. Illustrative Examples

In this section, we present two examples to illustrate the proposed methods.

Example 4.1. Consider a DFS (2.15) with parameters as

(4.1)

and d = 2, Δ_i(k) = diag {Δ_1i(k), Δ_2i(k), Δ_3i(k)}, where Δ_ji satisfies |Δ_ji(k)| ≤ 1 for all i = 1,2, j = 1,2, 3 and k ∈ ℤ⁺. The h₁ and h₂ are fuzzy sets defined as

(4.2)

Moreover, we assume the failure rate p = 0.4 and the recovery rate q = 0.8. Then, we choose R = I₃, δ_x = 1, N = 5, μ = 2, Theorem 3.6 yields ϵ = 21.8239 and

(4.3)

Thus, we can obtain the following state-feedback controller gains:

(4.4)

Furthermore, let R = I₃, δ_x = 1, N = 5, by Theorem 3.6, the optimal bound with minimum value of ϵ² relies on the parameter μ. We can find feasible solution when 1.20 ≤ μ ≤ 44.43. Figure 1 shows the optimal value with different value of μ. Noting that when μ = 1.4, it yields the optimal value ϵ = 13.7246. Then, by using the program fminsearch in the optimization toolbox of MATLAB starting at μ = 1.4, the locally convergent solution can be derived as

(4.5)

with μ = 1.3591 and the optimal value ϵ = 13.6304.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The local optimal bound of ϵ.

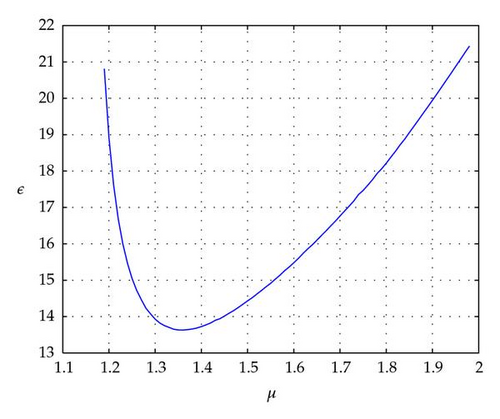
Example 4.2. Consider a DFS (2.15) with w(t) = 0 and

(4.6)

In addition, the other matrices parameters, fuzzy basis functions, and the failure rate p and the recovery rate q are the same as Example 4.1.

Then, let R = I₃, δ_x = 1, N = 6, by Corollary 3.7, the optimal bound with minimum value of ϵ² relies on the parameter μ. We can find feasible solution when 1 ≤ μ ≤ 23.61. Thus, the above system is stochastically stable and when μ = 1, it yields the optimal value ϵ = 4.5131 and the following optimized state-feedback controller gains:

(4.7)

5. Conclusions

This paper addresses the stochastic finite-time stability and stochastic finite-time boundedness problems for one family of fuzzy systems over networks with packet dropout. Taking into account the data packet drop being a time homogenous Markov process, thus the discrete-time DFS with packet loss can be described by one class of fuzzy Markovian jump systems. Then, state-feedback controllers are designed to guarantee the resulting closed-loop fuzzy discrete-time system with Markovian jumps SFTS and SFTB. The SFTS and SFTB criteria can be tackled in the form of linear matrix inequalities with a fixed parameter. As an auxiliary result, we also give sufficient conditions on the stochastic stability of the class of fuzzy systems with data packet dropout. Finally, simulation results are also given to demonstrate the validity of the proposed methodology.

Acknowledgments

The authors would like to thank the reviewers and editors for their very helpful comments and suggestions which could have improved the presentation of the paper. The paper was supported by the National Natural Science Foundation of China under Grant 60874006, supported by Doctoral Foundation of Henan University of Technology under Grant 2009BS048, supported by Foundation of Henan Educational Committee under Grant 2011A120003, and supported by Foundation of Henan University of Technology under Grant 09XJC011.

References

1 Brockett R. W. and Liberzon D., Quantized feedback stabilization of linear systems, IEEE Transactions on Automatic Control. (2000) 45, no. 7, 1279–1289, https://doi.org/10.1109/9.867021, 1779982, ZBL0988.93069.
10.1109/9.867021
Web of Science® Google Scholar
2 Liberzon D., Hybrid feedback stabilization of systems with quantized signals, Automatica. (2003) 39, no. 9, 1543–1554, https://doi.org/10.1016/S0005-1098(03)00151-1, 2143462, ZBL1030.93042.
10.1016/S0005-1098(03)00151-1
Web of Science® Google Scholar
3 Yu M., Wang L., Chu T., and Hao F., Stabilization of networked control systems with data packet dropout and transmission delays: continuous-time case, European Journal of Control. (2005) 11, no. 1, 40–55, https://doi.org/10.3166/ejc.11.40-49, 2155976.
10.3166/ejc.11.40-49
Web of Science® Google Scholar
4 Zhang X., Lu G., and Zheng Y., Stabilization of networked stochastic time-delay fuzzy systems with data dropout, IEEE Transactions on Fuzzy Systems. (2008) 16, no. 3, 798–807, 2-s2.0-45549099036, https://doi.org/10.1109/TFUZZ.2007.905921.
10.1109/TFUZZ.2007.905921
Web of Science® Google Scholar
5 Xiong J. and Lam J., Stabilization of linear systems over networks with bounded packet loss, Automatica. (2007) 43, no. 1, 80–87, https://doi.org/10.1016/j.automatica.2006.07.017, 2266772, ZBL1140.93383.
10.1016/j.automatica.2006.07.017
CAS Web of Science® Google Scholar
6 Bakule L. and De La Sen M., Decentralized stabilization of networked complex composite systems with nonlinear perturbations, 1–3, Proceedings of the 2009 IEEE International Conference on Control and Automation (ICCA ′09), December 2009, Christchurch, New Zealand, 2272–2277, 2-s2.0-77950424694, https://doi.org/10.1109/ICCA.2009.5410243.
10.1109/ICCA.2009.5410243
Google Scholar
7 Wang Y. L. and Yang G. H., State feedback control synthesis for networked control systems with packet dropout, Asian Journal of Control. (2009) 11, no. 1, 49–58, https://doi.org/10.1002/asjc.79, 2512998.
10.1002/asjc.79
Web of Science® Google Scholar
8 Tsumura K., Ishii H., and Hoshina H., Tradeoffs between quantization and packet loss in networked control of linear systems, Automatica. (2009) 45, no. 12, 2963–2970, 2-s2.0-70449707142, https://doi.org/10.1016/j.automatica.2009.09.030, ZBL1192.93074.
10.1016/j.automatica.2009.09.030
Web of Science® Google Scholar
9 Niu Y., Jia T., Wang X., and Yang F., Output-feedback control design for NCSs subject to quantization and dropout, Information Sciences. (2009) 179, no. 21, 3804–3813, https://doi.org/10.1016/j.ins.2009.07.006, 2568245, ZBL1171.93328.
10.1016/j.ins.2009.07.006
Web of Science® Google Scholar
10 Ishido Y., Takaba K., and Quevedo D. E., Stability analysis of networked control systems subject to packet-dropouts and finite-level quantization, Systems & Control Letters. (2011) 60, no. 5, 325–332, 2838896, https://doi.org/10.1016/j.sysconle.2011.02.008, ZBL1214.93010.
10.1016/j.sysconle.2011.02.008
Web of Science® Google Scholar
11 Imer O. C., Yuksel S., and Basar T., Optimal control of LTI systems over unreliable communication links, Automatica. (2006) 42, no. 9, 1429–1439, https://doi.org/10.1016/j.automatica.2006.03.011, 2246753, ZBL1128.93368.
10.1016/j.automatica.2006.03.011
Web of Science® Google Scholar
12 Wang Z., Ho W. C., and Liu X., Variance-constrained filtering for uncertain stochastic systems with missing measurements, IEEE Transactions on Automatic Control. (2003) 48, no. 7, 1254–1258, https://doi.org/10.1109/TAC.2003.814272, 1988100.
10.1109/TAC.2003.814272
Web of Science® Google Scholar
13 Wang Z., Ho W. C., and Liu X., Variance-constrained control for uncertain stochastic systems with missing measurements, IEEE Transactions on Systems, Man, and Cybernetics Part A. (2005) 35, no. 5, 746–753, 2-s2.0-27144501877, https://doi.org/10.1109/TSMCA.2005.851124.
10.1109/TSMCA.2005.851124
Web of Science® Google Scholar
14 Dong H., Wang Z., and Gao H., H^∞ fuzzy control for systems with repeated scalar nonlinearities and random packet losses, IEEE Transactions on Fuzzy Systems. (2009) 17, no. 2, 440–450, 2-s2.0-65549169625, https://doi.org/10.1109/TFUZZ.2009.2014223.
10.1109/TFUZZ.2009.2014223
Web of Science® Google Scholar
15 Zhao Y., Gao H., and Chen T., Fuzzy constrained predictive control of non-linear systems with packet dropouts, IET Control Theory & Applications. (2010) 4, no. 9, 1665–1677, https://doi.org/10.1049/iet-cta.2009.0274, 2757333.
10.1049/iet-cta.2009.0274
Web of Science® Google Scholar
16 Zhang J. and Xia Y., Design of H^∞ fuzzy controllers for nonlinear systems with random data dropouts, Optimal Control Applications and Methods. (2011) 32, no. 3, 328–349, https://doi.org/10.1002/oca.942.
10.1002/oca.942
CAS Web of Science® Google Scholar
17 Takagi T. and Sugeno M., Fuzzy identification of systems and its applications to modeling and control, IEEE Transactions on Systems, Man and Cybernetics. (1985) 15, no. 1, 116–132, 2-s2.0-0021892282, ZBL0576.93021.
10.1109/TSMC.1985.6313399
Web of Science® Google Scholar
18 Tanaka K. and Sugeno M., Stability analysis and design of fuzzy control systems, Fuzzy Sets and Systems. (1992) 45, no. 2, 135–156, https://doi.org/10.1016/0165-0114(92)90113-I, 1149415, ZBL0758.93042.
10.1016/0165-0114(92)90113-I
Web of Science® Google Scholar
19 Tanaka K., Ikeda T., and Wang H. O., Fuzzy regulators and fuzzy observers: relaxed stability conditions and LMI-based designs, IEEE Transactions on Fuzzy Systems. (1998) 6, no. 2, 250–265, 2-s2.0-0032070670, https://doi.org/10.1109/91.669023.
10.1109/91.669023
Web of Science® Google Scholar
20 Wang H. O., Tanaka K., and Griffin M. F., An approach to fuzzy control of nonlinear systems: stability and design issues, IEEE Transactions on Fuzzy Systems. (1996) 4, no. 1, 14–23, 2-s2.0-0030082891, https://doi.org/10.1109/91.481841.
10.1109/91.481841
Web of Science® Google Scholar
21 Tseng C. S., Chen B. S., and Uang H. J., Fuzzy tracking control design for nonlinear dynamic systems via T-S fuzzy model, IEEE Transactions on Fuzzy Systems. (2001) 9, no. 3, 381–392, 2-s2.0-0035360942, https://doi.org/10.1109/91.928735.
10.1109/91.928735
Web of Science® Google Scholar
22 Teixeira M. C. M., Assuncao E., and Avellar R. G., On relaxed LMI-based designs for fuzzy regulators and fuzzy observers, IEEE Transactions on Fuzzy Systems. (2003) 11, no. 5, 613–623, 2-s2.0-10744219783, https://doi.org/10.1109/TFUZZ.2003.817840.
10.1109/TFUZZ.2003.817840
Web of Science® Google Scholar
23 Guan X. P. and Chen C. L., Delay-dependent guaranteed cost control for T-S fuzzy systems with time delays, IEEE Transactions on Fuzzy Systems. (2004) 12, no. 2, 236–249, 2-s2.0-1942436728, https://doi.org/10.1109/TFUZZ.2004.825085, ZBL1142.93363.
10.1109/TFUZZ.2004.825085
Web of Science® Google Scholar
24 Feng G., A survey on analysis and design of model-based fuzzy control systems, IEEE Transactions on Fuzzy Systems. (2006) 14, no. 5, 676–697, 2-s2.0-33750268081, https://doi.org/10.1109/TFUZZ.2006.883415.
10.1109/TFUZZ.2006.883415
Web of Science® Google Scholar
25 Weiss L. and Infante E. F., Finite time stability under perturbing forces and on product spaces, IEEE Transactions on Automatic Control. (1967) 12, 54–59, 0209589, https://doi.org/10.1109/TAC.1967.1098483, ZBL0168.33903.
10.1109/TAC.1967.1098483
Web of Science® Google Scholar
26 Amato F., Ariola M., and Dorato P., Finite-time control of linear systems subject to parametric uncertainties and disturbances, Automatica. (2001) 37, no. 9, 1459–1463, 2-s2.0-0035452456, https://doi.org/10.1016/S0005-1098(01)00087-5, ZBL0983.93060.
10.1016/S0005-1098(01)00087-5
Web of Science® Google Scholar
27 Zhang W. and An X., Finite-time control of linear stochastic systems, International Journal of Innovative Computing, Information and Control. (2008) 4, no. 3, 689–696, 2-s2.0-63649087412.
Web of Science® Google Scholar
28 Ambrosino R., Calabrese F., Cosentino C., and De Tommasi G., Sufficient conditions for finite-time stability of impulsive dynamical systems, IEEE Transactions on Automatic Control. (2009) 54, no. 4, 861–865, https://doi.org/10.1109/TAC.2008.2010965, 2514824.
10.1109/TAC.2008.2010965
Web of Science® Google Scholar
29 Amato F. and Ariola M., Finite-time control of discrete-time linear systems, IEEE Transactions on Automatic Control. (2005) 50, no. 5, 724–729, https://doi.org/10.1109/TAC.2005.847042, 2141582.
10.1109/TAC.2005.847042
Web of Science® Google Scholar
30 Garcia G., Tarbouriech S., and Bernussou J., Finite-time stabilization of linear time-varying continuous systems, IEEE Transactions on Automatic Control. (2009) 54, no. 2, 364–369, https://doi.org/10.1109/TAC.2008.2008325, 2491966.
10.1109/TAC.2008.2008325
Web of Science® Google Scholar
31 Amato F., Ambrosino R., Ariola M., and Cosentino C., Finite-time stability of linear time-varying systems with jumps, Automatica. (2009) 45, no. 5, 1354–1358, https://doi.org/10.1016/j.automatica.2008.12.016, 2531617, ZBL1162.93375.
10.1016/j.automatica.2008.12.016
Web of Science® Google Scholar
32 Yang D. and Cai K. Y., Finite-time quantized guaranteed cost fuzzy control for continuous-time nonlinear systems, Expert Systems with Applications. (2010) 37, no. 10, 6963–6967, 2-s2.0-77950945658, https://doi.org/10.1016/j.eswa.2010.03.024.
10.1016/j.eswa.2010.03.024
Web of Science® Google Scholar
33 Amato F., Ariola M., and Cosentino C., Finite-time control of discrete-time linear systems: analysis and design conditions, Automatica. (2010) 46, no. 5, 919–924, 2-s2.0-77950626955, https://doi.org/10.1016/j.automatica.2010.02.008, ZBL1191.93099.
10.1016/j.automatica.2010.02.008
Web of Science® Google Scholar
34 He S. and Liu F., Robust finite-time stabilization of uncertain fuzzy jump systems, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 9, 3853–3862.
Web of Science® Google Scholar
35 He S. and Liu F., Stochastic finite-time boundedness of Markovian jumping neural network with uncertain transition probabilities, Applied Mathematical Modelling. (2011) 35, no. 6, 2631–2638, https://doi.org/10.1016/j.apm.2010.11.050, 2776185, ZBL1219.93143.
10.1016/j.apm.2010.11.050
Web of Science® Google Scholar
36 Krasovskii N. M. and A. Lidskii E., Analytical design of controllers in systems with random attributes, Automation and Remote Control. (1961) 22, no. 9–11, 1021–1025, 1141–1146, 1289–1294.
Google Scholar
37 Mao X., Stability of stochastic differential equations with Markovian switching, Stochastic Processes and their Applications. (1999) 79, no. 1, 45–67, https://doi.org/10.1016/S0304-4149(98)00070-2, 1666831, ZBL0962.60043.
10.1016/S0304-4149(98)00070-2
Web of Science® Google Scholar
38 de Souza C. E., Robust stability and stabilization of uncertain discrete-time Markovian jump linear systems, IEEE Transactions on Automatic Control. (2006) 51, no. 5, 836–841, https://doi.org/10.1109/TAC.2006.875012, 2232610.
10.1109/TAC.2006.875012
Web of Science® Google Scholar
39 Shi P., Xia Y., Liu G. P., and Rees D., On designing of sliding-mode control for stochastic jump systems, IEEE Transactions on Automatic Control. (2006) 51, no. 1, 97–103, https://doi.org/10.1109/TAC.2005.861716, 2192795.
10.1109/TAC.2005.861716
Web of Science® Google Scholar
40 Wu L., Shi P., and Gao H., State estimation and sliding-mode control of Markovian jump singular systems, IEEE Transactions on Automatic Control. (2010) 55, no. 5, 1213–1219, https://doi.org/10.1109/TAC.2010.2042234, 2642088.
10.1109/TAC.2010.2042234
CAS Web of Science® Google Scholar
41 Nguang S. K., Assawinchaichote W., and Shi P., Robust H-infinity control design for fuzzy singularly perturbed systems with Markovian jumps: an LMI approach, IET Control Theory & Applications. (2007) 1, no. 4, 893–908, https://doi.org/10.1049/iet-cta:20060369, 2348620.
10.1049/iet-cta:20060369
Web of Science® Google Scholar
42 Seiler P. and Sengupta R., An H^∞ approach to networked control, IEEE Transactions on Automatic Control. (2005) 50, no. 3, 356–364, https://doi.org/10.1109/TAC.2005.844177, 2123096.
10.1109/TAC.2005.844177
Web of Science® Google Scholar
43 Boyd S., Ghaoui L.E., Feron E., and Balakrishnan V., Linear Matrix Inequality in Systems and Control Theory, 1994, Society for Industrial and Applied Mathematics, Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics.
10.1137/1.9781611970777
Google Scholar

Citing Literature

All articles

On Stochastic Finite-Time Control of Discrete-Time Fuzzy Systems with Packet Dropout

Abstract

1. Introduction