Volume 2012, Issue 1 710172

Research Article

Open Access

Theoretical Analysis and Semianalytical Solutions for a Turbulent Buoyant Hydrogen-Air Jet

Corresponding Author

M. F. El-Amin

[email protected]

Computational Transport Phenomena Laboratory (CTPL), Physical Sciences and Engineering Division (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal , Jeddah 23955-6900, Saudi Arabia kaust.edu.sa

Department of Mathematics, Aswan Faculty of Science, South Valley University, Aswan 81528, Egypt svu.edu.eg

Search for more papers by this author

Shuyu Sun,

Shuyu Sun

Search for more papers by this author

Amgad Salama,

Amgad Salama

Search for more papers by this author

M. F. El-Amin,

Corresponding Author

M. F. El-Amin

[email protected]

Department of Mathematics, Aswan Faculty of Science, South Valley University, Aswan 81528, Egypt svu.edu.eg

Search for more papers by this author

Shuyu Sun,

Shuyu Sun

Search for more papers by this author

Amgad Salama,

Amgad Salama

Search for more papers by this author

First published: 20 February 2012

https://doi.org/10.1155/2012/710172

Citations: 1

Academic Editor: Hiroshi Kanayama

Share a link

Email
Wechat
Bluesky

Abstract

Semianalytical solutions are developed for turbulent hydrogen-air plume. We derived analytical expressions for plume centerline variables (radius, velocity, and density deficit) in terms of a single universal function, called plume function. By combining the obtained analytical expressions of centerline variables with empirical Gaussian expressions of the mean variables, we obtain semianalytical expressions for mean quantities of hydrogen-air plume (velocity, density deficit, and mass fraction).

1. Introduction

One of the important safety issues of hydrogen energy is the hydrogen leakage into ambient air and the associated risk of fire or explosion. In fact, industry has already produced several prototype products using hydrogen as a fuel. Unfortunately, these products are not yet available for commercial use because of safety concerns related to hydrogen leakage. So studying hydrogen-air behavior is very important in order to estimate expected hazards from leakage as well as to propose recommendations when designing hydrogen-related facilities.

Recently, El-Amin and coauthors [1–6] studied the problem of hydrogen leakage in air. In [1–3], they introduced boundary layer theory approach to model the concentration layer adjacent to a ceiling wall at the impinging and far regions in both planar and axisymmetric cases for small-scale hydrogen leakage. While in [4–6], they studied the turbulent hydrogen-air jet/plume resulted from hydrogen leakage in open air. The laminar hydrogen jet is analyzed by Sánchez–Sanz et al. [7]. Also, experimental measurements for turbulent hydrogen jet have been performed by Schefer and coauthors (e.g., [8–10]). On the other hand, CFD simulations of the problem have been done by many researcher such as Matssura and coauthors [11–14], Kikukawa [15], Agarant et al.[16], and Swain et al. [17, 18].

Hydrogen-air jet is an example of non-Boussinesq plume; since the initial fractional density difference is high. The initial fractional density difference is defined as Δρ₀/ρ_∞ = (ρ_∞ − ρ₀)/ρ_∞, where ρ₀ is the initial centerline density (density at the source) and ρ_∞ is the ambient density. As an example, the initial fractional density differences for selected binary low-density gases at temperature 15°C are 0.93 for H₂-Air, 0.86 for He-Air, 0.43 for CH₄-Air, and 0.06 for C₂H₂-N₂. Crapper and Baines [19] suggested that the upper bound of applicability of the Boussinesq approximation is that the initial fractional density difference Δρ₀/ρ_∞ does not exceed 0.05. In general, one can say that the Boussinesq approximation is valid for small initial fractional density difference, Δρ₀/ρ_∞ ≪ 1 (e.g., El-Amin and Kanayama [5]). This is correct only for the case of a plume produced by a positive source of buoyancy, that is, a plume composed of fluid less dense than the ambient. For the cases where this criterion is not met, Boussinesq approximation may not be used and a density equation needs to be incorporated. El-Amin [6] introduced a numerical investigation of a non-Boussinesq, low-density gas jet (hydrogen) leaking into a high-density ambient (air). The integral models of jet fluxes are obtained and transformed into a set of ordinary differential equations of the mean centerline quantities. Therefore, mean quantities are obtained in addition to cross-stream velocity, Reynolds stresses, and turbulent Schmidt number. Furthermore, the normalized jet-feed material density and momentum flux density are correlated.

It is worth mentioning that theoretical developments and analysis of jet/plume theory were studied by a number of authors since 1950s (see, e.g., Morton et al. [20]; Morton [21]; Morton and Middleton [22]; Delichatsios [23]; Rooney and Linden [24]; Hunt and Kaye [25, 26]; Carlotti and Hunt [27]). Recently, Michaux and Vauquelin [28] developed analytical solutions for centerlines quantities of turbulent plumes rising from circular sources of positive buoyancy in a quiescent environment of uniform density for both Boussinesq and non-Boussinesq cases.

In this paper, semianalytical solution and theoretical analysis are developed for round hydrogen jet leaking into air based on Michaux and Vauquelin [28]. It is assumed that the rate of entrainment is a function of the plume centerline velocity and the ratio of the mean plume and ambient densities. Analytical expressions for all plume variables (radius, velocity, and density deficit) in terms of plume function for a given source parameter are derived.

2. Mathematical Analysis and Similarity Solutions

2.1. Governing Equations

Consider a vertical axisymmetric hydrogen-air buoyant jet resulting from a small-scale hydrogen leakage in the air with a finite circular source. Using cylindrical polar coordinates (z, r) with the z-axis vertical, the source is located at z = 0. The continuity, momentum, and concentration equations in cylindrical coordinate system (Figure 1) for the steady vertical axisymmetric buoyant free jet can be written as [29]:

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of turbulent hydrogen-air jet.

where U is the mean streamwise velocity, and V is the mean cross-stream velocity, and C is the hydrogen concentration (mass fraction). The overbar denotes the time-averaged quantities, u, v are the components of velocity fluctuations in z, r directions, respectively, c is the concentration fluctuation, and ρ is the mixture density.

On the other hand, from the experimental observations, the equations for the vertical velocity, density deficiency, and mass fraction profiles, assuming that the hydrogen-air mixture behaves as an ideal gas, are as follows (Fisher et al. [30], Hussein et al. [31], Shabbir and George [32], and Schefer et al. [9, 10]):

()

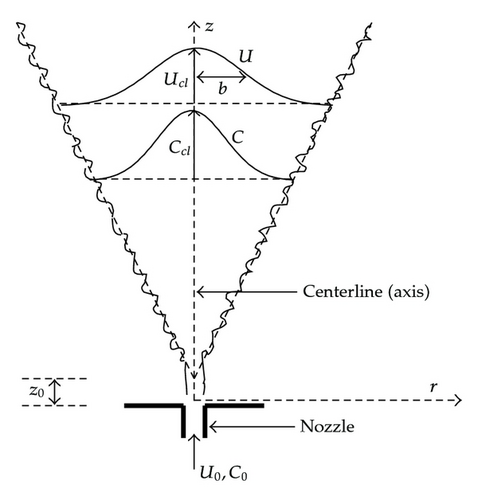
where U(r, z) and ρ(r, z) are the mean velocity and mean density at any point of the jet body; U_cl(z) and ρ_cl(z) are the centerline velocity and density. b(z) = c_m(z − z₀) is the jet/plume width which increases linearly with z, c_m is the momentum spread rate of the jet. z₀ is the virtual origin, which is the distance above/below the orifice where the flow appears to originate. The experimentally measured spread rate c_m varies in the range 0.1–0.13. The buoyancy spreading factor λ = c_m/c_c expresses the ratio of spreading rates between the velocity and density deficiency profiles. The corresponding streamwise concentration for the axisymmetric hydrogen-air, free jet as detected experimentally by Schefer et al. [10] is given as C = C_clexp (−0.693 r²/b²). In general, the spread rate for the concentration c_c is given in the formula . In the work of Schefer et al. [10], the momentum spread rate for the case of hydrogen jet was estimated as c_m = 0.103, from which one can find c_c = 0.124, and λ = 0.832. It is well known that c_C ≠ c_m, that is, velocity and density spread at different rates.

2.2. Similarity Solutions

Integrating the continuity (2.1) radially gives

()

Since U(r, z) is negligible for r > b, then integrating (2.1) for b < r < ∞ gives

()

This implies that

()

where V_e denotes the inflow velocity at the plume edge which is known as the entrainment velocity. Therefore, we have

()

This equation indicates that the increase in plume volume flux is supplied by a radial influx from the far field which in turn implies a flow across the plume boundary b. Batchelor [33] concluded that a vigorous entrainment of the ambient will be obtained as the density ratio tends to unity, ρ_cl/ρ_∞ → 1. While as the density ratio tends to zero, ρ_cl/ρ_∞ → 0, the entrainment falls to zero. Between these two limits, there will be a smooth transition of entrainment pattern. The experiments by Ricou and Spalding [34] suggest that the entrainment velocity may be obtained using the following formula

()

where α is the entrainment coefficient.

Also, Morton [35] assumed that the rate of entrainment into a strongly buoyant plume is a function of both density ratio ρ_cl/ρ_∞ and Reynolds stresses which have a magnitude proportional to

. Therefore, the local entrainment velocity may be obtained as

, which has also been suggested by Thomas [36], Steward [37], and Townsend [38]. Therefore, (2.11) can be written in the form

()

For calculating the momentum flux, let us integrate (2.2) with respect to r, from r = 0 to r = ∞, noting that

and

, we get

()

Similarly, for concentration flux, integrating (2.3) with respect to r from r = 0 to r = ∞, noting also that

and

, we get

()

This equation may be equivalent to the buoyancy flux equation which can be written in the following form [19]:

()

Substituting (2.4)–(2.6) into (2.16), one obtains

()

Substituting (2.5), (2.6), and (2.17) into (2.13), (2.14), and (2.15) gives

()

In homogeneous surroundings of density ρ_∞, the density deficit flux, (2.17), is equivalent to

()

which has the dimension of a buoyancy flux.

Recently, Michaux and Vauquelin [28] developed analytical solutions for centerlines quantities of turbulent plumes. Now, let us introduce a modified radius β and a dimensionless density deficit η [28]:

()

Therefore, (2.17)–(2.19) can be rewritten in the following form:

()

In the previous work of El-Amin and Kanayama [5] and El-Amin [6], they developed the similarity formulation and numerical solutions of the centerline quantities such as velocity and concentration.

In the current work, we follow the work of Michaux and Vauquelin [28] to obtain analytical/semianalytical solutions for centerline plume quantities. Using

, and η(z) = C_ηz^p, the constants

and C_η; exponents m, n, p can be determined to obtain similarity solutions for β, U_cl, and η as

()

z in these expressions may be replaced by z − z₀ to adapt solutions at near-source region and z₀ is virtual origin.

2.3. Plume Function and Source Parameter

Now, let us introduce the plume function as [28]:

()

At source (z = 0), Γ(0) = Γ₀, corresponding to the source parameter initially introduced by Morton [21] and defined as [26]:

()

where Q, M, and B_f are the initial values of specific mass flux, specific momentum flux, and specific buoyancy flux, respectively, defined as

()

d is the inlet diameter, U₀ is velocity at source, and Δρ_∞ is the difference in density between the receiving fluid and the fluid being discharged. Based on source parameter value Morton and Middleton [22] have categorized plumes with positive buoyancy as simple (pure) plume (Γ₀ = 1), forced plume (Γ₀ < 1), and lazy plume (Γ₀ > 1). Other possibilities (Hunt and Kaye [25]) for Γ₀ = 0, flow is pure jet without buoyancy, and, for Γ₀ < 0, flow is weak fountains (negative buoyancy).

For hydrogen-air plume the source parameter is Γ₀ ≪ 1 (of order 10⁻⁴), so, based on Morton et al. [20] classification, it is a forced plume.

Equation (2.22) can be rewritten in terms of Γ as follow:

()

Using plume function Γ, (2.24), and (2.27)–(2.29), we may write

()

One can deduce that for Γ₀ < 1, Γ increases monotonically with height and tends asymptotically toward unity.

Using (2.27) and (2.30), one may get

()

Integrating this equation subject to the source conditions, one obtains

()

therefore,

()

Similarly, we can find that

()

therefore,

()

Finally, using (2.24), (2.32), and (2.34), we get

()

Now, Γ is a function of z to relate each plume variable to z. Substituting (2.32) into (2.30), one gets

()

where

, and

is the characteristic length defined from initial plume condition. For the case under consideration, we find Λ₀ = 0.17.

Integrating (2.38), one obtains

()

The above integration function has no explicit form, so Michaux and Vauquelin [28] computed and tabulated the integral function ℑ(X) for several values of X. Unfortunately, they did not provide very small values as we find in this investigation when the source parameter is Γ₀ ≪ 1 (of order 10⁻⁴). Alternatively, we can write the integration function as

()

where

is the hypergeometric function defined by

()

But Γ ≪ 1 is very small (of order 10⁻⁴) for the case of hydrogen-air plume, so two terms of the above series can approximate the function. Thus,

()

This may lead to

()

According to this relation, ℑ(Γ₀) = 0.039294, therefore,

()

From (2.43) and (2.44), one gets

()

Again from (2.43), we can determine values of Γ from ℑ(Γ) given by (2.44). It is clear that Γ decreases as ℑ(Γ) increases and ℑ(Γ) increases as z increases. Thus, Γ decreases as z increases and the maximum value of Γ is located at z = 0, which is equal to Γ₀. Therefore, using (2.36), one can find U_cl/U₀ = 1, and the maximum velocity is U_cl = U₀.

Finally, by combining (2.4)–(2.6) with (2.33), (2.36), and (2.37), one can obtain analytical expressions for vertical velocity, density deficiency, and mass fraction for hydrogen-air mixture in terms of the universal variable Γ as follows:

()

3. Conclusion

This paper introduces the reader to a set of features of hydrogen-air plume, which is very important to assess the potential hazard resulting from hydrogen sources upon leakage into the ambient atmosphere. Throughout this work, we derived profiles of the mean quantities for a turbulent hydrogen-air plume. These mean quantities, such as plume radius, velocity, and density deficit, are expressed in terms of the plume function for a given source parameter. These quantities are determined by integral relations and by analysis using similarity variables. Therefore, mean quantities are expressed solely in terms of the plume function and the source parameter. The plume function is valid for a range of small values of Γ as required for hydrogen-air plume. The hypergeometric function is exploited, and the profiles of the mean quantities are obtained. These results may be generalized and extended in a future work to cover more complex flow types found in a prober accident of hydrogen leaks such as leakage in hydrogen station.

References

1 El-Amin M. F. and Kanayama H., Boundary layer theory approach to the concentration layer adjacent to a ceiling wall at impinging region of a hydrogen leakage, International Journal of Hydrogen Energy. (2008) 33, no. 21, 6393–6400, 2-s2.0-55049115237, https://doi.org/10.1016/j.ijhydene.2008.07.116.
10.1016/j.ijhydene.2008.07.116
CAS Web of Science® Google Scholar
2 El-Amin M. F., Inoue M., and Kanayama H., Boundary layer theory approach to the concentration layer adjacent to a ceiling wall of a hydrogen leakage: far region, International Journal of Hydrogen Energy. (2008) 33, no. 24, 7642–7647, 2-s2.0-57549111532, https://doi.org/10.1016/j.ijhydene.2008.09.047.
10.1016/j.ijhydene.2008.09.047
CAS Web of Science® Google Scholar
3 El-Amin M. F. and Kanayama H., Boundary layer theory approach to the concentration layer adjacent to the ceiling wall of a hydrogen leakage: axisymmetric impinging and far regions, International Journal of Hydrogen Energy. (2009) 34, no. 3, 1620–1626, 2-s2.0-58749094601, https://doi.org/10.1016/j.ijhydene.2008.11.064.
10.1016/j.ijhydene.2008.11.064
CAS Web of Science® Google Scholar
4 El-Amin M. F. and Kanayama H., Integral solutions for selected turbulent quantities of small-scale hydrogen leakage: a non-buoyant jet or momentum-dominated buoyant jet regime, International Journal of Hydrogen Energy. (2009) 34, no. 3, 1607–1612, 2-s2.0-58649094650, https://doi.org/10.1016/j.ijhydene.2008.11.067.
10.1016/j.ijhydene.2008.11.067
CAS Web of Science® Google Scholar
5 El-Amin M. F. and Kanayama H., Similarity consideration of the buoyant jet resulting from hydrogen leakage, International Journal of Hydrogen Energy. (2009) 34, no. 14, 5803–5809, 2-s2.0-67650713590, https://doi.org/10.1016/j.ijhydene.2009.05.059.
10.1016/j.ijhydene.2009.05.059
CAS Web of Science® Google Scholar
6 El-Amin M. F., Non-Boussinesq turbulent buoyant jet resulting from hydrogen leakage in air, International Journal of Hydrogen Energy. (2009) 34, no. 18, 7873–7882, 2-s2.0-69349088482, https://doi.org/10.1016/j.ijhydene.2009.07.061.
10.1016/j.ijhydene.2009.07.061
CAS Web of Science® Google Scholar
7 Sánchez-Sanz M., Rosales M., and Sánchez A. L., The hydrogen laminar jet, International Journal of Hydrogen Energy. (2010) 35, no. 8, 3919–3927, 2-s2.0-77950300274, https://doi.org/10.1016/j.ijhydene.2010.01.081.
10.1016/j.ijhydene.2010.01.081
CAS Web of Science® Google Scholar
8 Houf W. G. and Schefer R. W., Analytical and experimental investigation of small-scale unintended releases of hydrogen, International Journal of Hydrogen Energy. (2008) 33, no. 4, 1435–1444, 2-s2.0-39849103402, https://doi.org/10.1016/j.ijhydene.2007.11.031.
10.1016/j.ijhydene.2007.11.031
CAS Web of Science® Google Scholar
9 Sehefer R. W., Houf W. G., and Williams T. C., Investigation of small-scale unintended releases of hydrogen: momentum-dominated regime, International Journal of Hydrogen Energy. (2008) 33, no. 21, 6373–6384, 2-s2.0-55049096838, https://doi.org/10.1016/j.ijhydene.2008.05.041.
10.1016/j.ijhydene.2008.05.041
Web of Science® Google Scholar
10 Schefer R. W., Houf W. G., and Williams T. C., Investigation of small-scale unintended releases of hydrogen: buoyancy effects, International Journal of Hydrogen Energy. (2008) 33, no. 17, 4702–4712, 2-s2.0-50849140814, https://doi.org/10.1016/j.ijhydene.2008.05.091.
10.1016/j.ijhydene.2008.05.091
CAS Web of Science® Google Scholar
11 Matsuura K., Effects of the geometrical configuration of a ventilation system on leaking hydrogen dispersion and accumulation, International Journal of Hydrogen Energy. (2009) 34, no. 24, 9869–9878, 2-s2.0-71749109179, https://doi.org/10.1016/j.ijhydene.2009.09.044.
10.1016/j.ijhydene.2009.09.044
CAS Web of Science® Google Scholar
12 Matsuura K., Nakano M., and Ishimoto J., Forced ventilation for sensing-based risk mitigation of leaking hydrogen in a partially open space, International Journal of Hydrogen Energy. (2010) 35, no. 10, 4776–4786, 2-s2.0-77951122622, https://doi.org/10.1016/j.ijhydene.2010.02.068.
10.1016/j.ijhydene.2010.02.068
CAS Web of Science® Google Scholar
13 Matsuura K., Nakano M., and Ishimoto J., The sensing-based adaptive risk mitigation of leaking hydrogen in a partially open space, International Journal of Hydrogen Energy. (2009) 34, no. 20, 8770–8782, 2-s2.0-70349451565, https://doi.org/10.1016/j.ijhydene.2009.08.013.
10.1016/j.ijhydene.2009.08.013
CAS Web of Science® Google Scholar
14 Matsuura K., Kanayama H., Tsukikawa H., and Inoue M., Numerical simulation of leaking hydrogen dispersion behavior in a partially open space, International Journal of Hydrogen Energy. (2008) 33, no. 1, 240–247, 2-s2.0-38349169066, https://doi.org/10.1016/j.ijhydene.2007.08.028.
10.1016/j.ijhydene.2007.08.028
CAS Web of Science® Google Scholar
15 Kikukawa S., Consequence analysis and safety verification of hydrogen fueling stations using CFD simulation, International Journal of Hydrogen Energy. (2008) 33, no. 4, 1425–1434, 2-s2.0-39849111458, https://doi.org/10.1016/j.ijhydene.2007.11.027.
10.1016/j.ijhydene.2007.11.027
CAS Web of Science® Google Scholar
16 Agarant V., Cheng Z., and Tchouvelev A., CFD modeling of hydrogen releases and dispersion in hydrogen energy station, Proceedings of the 15th World Hydrogen Energy Conference, 2004.
Google Scholar
17 Swain M. R. and Swain M. N., Passive ventilation systems for the safe use of hydrogen, International Journal of Hydrogen Energy. (1996) 21, no. 10, 823–835, 2-s2.0-0030269719, https://doi.org/10.1016/0360%2D3199(96)00002%2DX.
10.1016/0360-3199(96)00002-X
CAS Web of Science® Google Scholar
18 Swain M. R., Filoso P., Grilliot E. S., and Swain M. N., Hydrogen leakage into simple geometric enclosures, International Journal of Hydrogen Energy. (2003) 28, no. 2, 229–248, 2-s2.0-1942504817, https://doi.org/10.1016/S0360%2D3199(02)00048%2D4.
10.1016/S0360-3199(02)00048-4
CAS Web of Science® Google Scholar
19 Crapper P. F. and Baines W. D., Non Boussinesq forced plumes, Atmospheric Environment. (1977) 11, 415–420, 2-s2.0-0017710901, https://doi.org/10.1016/0004%2D6981(77)90002%2D6.
10.1016/0004-6981(77)90002-6
Web of Science® Google Scholar
20 Morton B. R., Taylor G., and Turner J. S., Turbulent gravitational convection from maintained and instantaneous sources, Proceedings of the Royal Society A. (1956) 234, 1–23, 0103671, https://doi.org/10.1098/rspa.1956.0011, ZBL0074.45402.
10.1098/rspa.1956.0011
Web of Science® Google Scholar
21 Morton B. R., Forced plumes, Journal of Fluid Mechanics. (1959) 5, 151–163, 0103670, https://doi.org/10.1017/S002211205900012X, ZBL0126.42903.
10.1017/S002211205900012X
Web of Science® Google Scholar
22 Morton B. R. and Middleton J., Scaling diagram for forced plumes, The Journal of Fluid Mechanics. (1973) 58, 165–176, https://doi.org/10.1017/S002211207300220X.
10.1017/S002211207300220X
Web of Science® Google Scholar
23 Delichatsios M. A., Strong turbulent buoyant plumes. I. Similarity, Combustion Science and Technology. (1981) 24, 191–195.
10.1080/00102208008952437
Web of Science® Google Scholar
24 Rooney G. G. and Linden P. F., Similarity considerations for non-Boussinesq plumes in an unstratified environment, The Journal of Fluid Mechanics. (1996) 318, 237–250, 2-s2.0-0030186056, https://doi.org/10.1017/S0022112096007100, ZBL0871.76097.
10.1017/S0022112096007100
CAS Web of Science® Google Scholar
25 Hunt G. R. and Kaye N. G., Virtual origin correction for lazy turbulent plumes, The Journal of Fluid Mechanics. (2001) 435, 377–396, 2-s2.0-0035947218, https://doi.org/10.1017/S0022112001003871, ZBL1022.76023.
10.1017/S0022112001003871
Web of Science® Google Scholar
26 Hunt G. R. and Kaye N. B., Lazy plumes, The Journal of Fluid Mechanics. (2005) 533, 329–338, https://doi.org/10.1017/S002211200500457X, 2263312, ZBL1074.76057.
10.1017/S002211200500457X
Web of Science® Google Scholar
27 Carlotti P. and Hunt G. R., Analytical solutions for turbulent non-Boussinesq plumes, The Journal of Fluid Mechanics. (2005) 538, 343–359, https://doi.org/10.1017/S0022112005005379, 2263223, ZBL1108.86002.
10.1017/S0022112005005379
Web of Science® Google Scholar
28 Michaux G. and Vauquelin O., Solutions for turbulent buoyant plumes rising from circular sources, Physics of Fluids. (2008) 20, no. 6, 2-s2.0-47149102346, https://doi.org/10.1063/1.2926758, 066601, ZBL1182.76515.
10.1063/1.2926758
Web of Science® Google Scholar
29 El-Amin M. F. and Sun S., M. F. El-Amin, Turbulent buoyant jet of a low-density gas leaks into a high-density ambient: hydrogen leakage in air, Advanced Topics in Mass Transfer, 2011, INTECH.
10.5772/15345
Google Scholar
30 Fischer H. B., List E. J., Koh R. C. Y., Imberger J., and Brooks N. H., Mixing in Inland and Coastal Waters, 1979, Academic Press.
Google Scholar
31 Hussein H. J., Capp S. P., and George W. K., Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet, The Journal of Fluid Mechanics. (1994) 258, 31–75, 2-s2.0-0027927141, https://doi.org/10.1017/S002211209400323X.
10.1017/S002211209400323X
CAS Web of Science® Google Scholar
32 Shabbir A. and George W. K., Experiments on a round turbulent buoyant plume, The Journal of Fluid Mechanics. (1994) 275, 1–32, 2-s2.0-0028668096, https://doi.org/10.1017/S0022112094002260.
10.1017/S0022112094002260
Web of Science® Google Scholar
33 Batchelor G. K., Heat convection and buoyancy effects in fluids, Quarterly Journal of the Royal Meteorological Society. (1954) 80, 339–358.
10.1002/qj.49708034504
Web of Science® Google Scholar
34 Ricou F. P. and Spalding D. B., Measurements of entrainment by axisymmetrical turbulent jets, The Journal of Fluid Mechanics. (1961) 8, 21–32, ZBL0098.41104.
10.1017/S0022112061000834
Web of Science® Google Scholar
35 Morton B. R., Modelling fire plumes, Proceedings of the 10th International Symposium on Combustion, 1965, 973–982.
Google Scholar
36 Thomas P. H., The size of flames from natural fires, Proceedings of the 9th Symposium on Combustion, 1963, 844–859.
Google Scholar
37 Steward F. R., Prediction of the height of turbulent diffusion buoyant flames, Combustion Science and Technology. (1970) 2, 203–212, https://doi.org/10.1080/00102207008952248.
10.1080/00102207008952248
Web of Science® Google Scholar
38 Townsend A. A., The mechanism of entrainment in free turbulent flows, The Journal of Fluid Mechanics. (1966) 26, 689–715, https://doi.org/10.1017/S0022112066001472.
10.1017/S0022112066001472
Web of Science® Google Scholar

Citing Literature

All articles

Theoretical Analysis and Semianalytical Solutions for a Turbulent Buoyant Hydrogen-Air Jet

Abstract

1. Introduction