We use the idea of nonstandard finite difference methods to derive the discrete variational integrators for multisymplectic PDEs. We obtain a nonstandard finite difference variational integrator for linear wave equation with a triangle discretization and two nonstandard finite difference variational integrators for the nonlinear Klein-Gordon equation with a triangle discretization and a square discretization, respectively. These methods are naturally multisymplectic. Their discrete multisymplectic structures are presented by the multisymplectic form formulas. The convergence of the discretization schemes is discussed. The effectiveness and efficiency of the proposed methods are verified by the numerical experiments.

1. Introduction

It is a fundamental approach to develop the discrete multisymplectic numerical methods based on the discrete Hamilton’s principle, because it leads in a natural way to multisymplectic integrators [1]. The discrete Euler-Lagrange equation is produced in the discrete variational principle [2–4]; meanwhile, the discrete multisymplectic structure is also generated [5, 6]. In the other words, the discrete variational integrators are multisymplectic automatically.

1.1. Multisymplectic Structure of Discrete Variational Integrators

By the Hamilton’s principle [6–9], the discrete multisymplectic structure which is preserved by the discrete variational integrator, is described by Poincaré-Cartan forms, in a differential geometric language. In paper [6], Marsden et al. showed how to obtain this structure directly from the variational principle, on the Lagrangian side. They defined it as the multisymplectic form formula, and they showed that it was conserved by the discrete variational integrator.

Lemma 1.1. If u is a solution of discrete Euler-Lagrange equation and V, W are first variations of u, then the following discrete multsisymplectic form formula holds:

(1.1)

The details of this conclusion could be referred to papers [5, 6]. This conclusion states that the discrete variational principles produce discrete variational integrators, and the multisymplecticity of these variational integrators is presented by the discrete multisymplectic form formula (1.1).

Vankerschaver et al. [10] revisited the multisymplectic form formula [6], showing that it could be obtained from the boundary Lagrangian that they defined in their paper. They presented an easy way to derive discrete multisymplectic form formula from discrete variational principle, using the notations of Poincaré-Cartan forms. In this paper, we follow the same way to derive the discrete multisymplectic form formulas of our discrete variational integrators.

When we use the discrete variational principle, we need to make a approximation of the Lagrangian. Here, in our paper, we would use nonstandard finite difference methods, instead of standard finite difference, to approximate the Lagrangian function, and derive the corresponding discrete variational integrators.

1.2. Nonstandard Finite Difference Methods

The nonstandard finite difference schemes are well developed by Mickens [11–15] in the past decades. These schemes are developed for compensating the weaknesses that may be caused by standard finite difference methods, for example, the numerical instabilities. Regarding the positivity of solutions, boundedness, and monotonicity of solutions, nonstandard finite difference schemes have a better performance than standard finite difference schemes, due to its flexibility to construct a nonstandard finite difference scheme that can preserve certain properties and structures, which are obeyed by the original equations. Also, the dynamic consistency could be presented well by nonstandard finite difference scheme. These advantages of nonstandard finite difference methods have been shown in many numerical applications. GonzLez-Parra et al. [16–18] developed nonstandard finite difference methods to solve population or biological models. The positivity condition and the conservation law of population dynamics are preserved by nonstandard finite difference schemes. Jordan [19] and Malek [20] constructed nonstandard finite difference schemes for heat transfer problems. For the symplectic systems, Mickens [15] derived the nonstandard finite difference variational integrator for symplectic ODEs. Ma et al. [21] developed the nonstandard finite difference variational integrator in stochastic ordinary differential equations.

The initial foundation of nonstandard finite difference methods is formed by the exact finite difference schemes [22]. After generalizing these results, Mickens summarizes the following three basic rules to construct nonstandard finite difference schemes.

(1) The orders of the discrete derivatives should be equal to the orders of the corresponding derivatives appearing in the differential equations.
Note. If the orders of the discrete derivatives are larger than those occurring in the differential equations, then numerical instabilities will in general occur.
(2) Discrete representations for derivatives must, in general, have nontrivial denominator functions.
Note. For example, the discrete first-derivative is generally represented by
(1.2)
where the numerator functions ψ(Δt) and the denominator functions ϕ(Δt) satisfy
(1.3)
(3) Both linear and nonlinear terms should be represented by nonlocal discrete representations on the discrete computational lattice.
Note. For example,
(1.4)

In our paper, we combine the advantages of nonstandard finite difference methods and discrete variational principles to construct nonstandard finite difference variational integrators, for two multisymplectic PDEs. These integrators are multysimplectic and their multysimplecticity are presented by their discrete multisymplectic form formulas, respectively.

In Section 2, we consider a simple linear wave equation. With the triangle discretization, we define the discrete Lagrangian using the idea of nonstandard finite difference and derive discrete variational integrator and the corresponding multisymplectic form formula, by discrete variational principle. The convergence of this method is analyzed. In Section 3, for the nonlinear Klein-Gordon equation, triangle discretization and square discretization are considered to obtain the nonstandard finite difference variational integrators. The discrete multisymplectic structures are presented, respectively. The convergence orders of the two methods are also discussed, and the convergence orders are shown in error tables in the numerical experiment section. Section 4 is devoted to showing the numerical behaviors of the developed nonstandard finite difference variational integrators.

2. Nonstandard Finite Difference Variational Integrator for Linear Wave Equation

We first consider a simple linear wave equation,

(2.1)

where u(x, t) is a scalar field function with two independent variables, x and t.

This linear wave equation is actually a multisymplectic PDE. As a classical and simple multisymplectic example, wave equation and its multisymplectic structure have been studied from both Hamiltonian [23–28] and Lagrangian viewpoints [3, 5, 6, 10]. Based on the Lagrangian viewpoint, we could also obtain (2.1) from the Euler-Lagrange equation

(2.2)

with the Lagrangian function L(u, u_t, u_x),

(2.3)

Assume that we have a uniform quadrangular mesh in the base space, with mesh lengths Δx and Δt. The nodes in this mesh are denoted by (i, j) ∈ ℤ × ℤ, corresponding to the points (x_i, t_j): = (iΔx, jΔt) in ℝ². We denote the value of the field u at the node (i, j) by

. We label the triangle at (i, j) with three ordered triple ((i, j), (i + 1, j), (i, j + 1)) as ∆_ij, and we define X_∆ to be the set of all such triangles. Then the discrete jet bundle [6, 10] is defined as follows:

(2.4)

which is equal to X_∆ × ℝ³.

Now we use nonstandard finite difference to define the discrete Lagrangian L_d on

, which is the discrete version of Lagrangian density [10, 29],

(2.5)

where denominator functions ϕ(Δt) and ψ(Δx) are defined according the exact solution of wave equation [5, 6, 12]

(2.6)

We have followed the rules of constructing nonstandard finite difference schemes in Mickens’ papers [11–15].

(1)
The discrete first-derivative is represented by
(2.7)
where denominator functions ϕ(Δt), ψ(Δx) are defined in (2.6). Using Taylor series expansion,
(2.8)
Then the denominator functions satisfy
(2.9)
(2)
Nonlocal representation on the discrete computational lattice are used here by
(2.10)

So, for the linear wave equation (2.1) with the Lagrangian (2.3), the discrete Lagrangian becomes

(2.11)

By the discrete Hamilton’s principle [6, 10], we have the discrete Euler-Lagrange equation,

(2.12)

where

and

are defined similarly as (2.11), which are

(2.13)

After some simple calculations, the discrete Euler-Lagrange equation (2.12) becomes

(2.14)

We could find that this scheme is symmetric in (i, j + 1) and (i, j − 1), (i + 1, j) and (i − 1, j). This is the nonstandard finite difference variational integrator, for the linear wave equation.

As we mentioned in Section 1 and Lemma 1.1, the advantages of deriving the multisymplectic numerical schemes from discrete variational principle are that they are naturally multisymplectic and the discrete multisymplectic structures are also generated in the variational principle. Now it is meaningful to show the multisymplectic structure of this discrete variational integrator (2.14) based on nonstandard finite difference method.

Since we consider triangulation discretization here, we focus on three adjacent triangles around

, denote this area by U. Following the idea in [10], the discrete boundary Lagrangian is given by

(2.15)

where

(2.16)

Taking twice exterior derivative of both sides, we have, by the fact that d²L_∂U ≡ 0, the discrete multisymplectic form formula with following form [10]:

(2.17)

where

(for k = 1,2, 3). The discrete Poincaré-Cartan forms

, and

are defined by

(2.18)

and similarly for

and

. Thus, for the linear wave equation (2.1), the multisymplectic form formula of this scheme (2.14) based on nonstandard finite difference method can be obtained as follows:

(2.19)

Now we have the first conclusion.

Theorem 2.1. The nonstandard finite difference variational integrator (2.14),

(2.20)

for linear wave equation (2.1) is multisymplectic, and the discrete multisymplectic structure is

(2.21)

We now discuss the convergence of this variational integrator (2.14) based on the nonstandard finite difference method. From the Lax equivalence theorem we know that, for a well-posed linear initial value problem, the consistent finite difference method is convergent if and only if it is stable.

By Taylor series expansion, we have

(2.22)

Similarly,

(2.23)

The above two equations show that the scheme is consistent and the truncation error for the integrator (2.14) is 𝒪((Δt) ² + (Δx) ²).

To explore the stability of the nonstandard finite difference variational integrator (2.14), we introduce the following notations:

(2.24)

Then the three-level explicit integrator (2.14) is equivalent to the following two-level scheme:

(2.25)

By using the Von Neumann method [30], we could get the amplification matrix of the above scheme,

(2.26)

where r = ϕ(Δt)/ψ(Δx). Note that, in the above matrix,

. Let η = 4r²sin²(βΔx). We have the characteristic equation

(2.27)

and the eigenvalues

(2.28)

When |λ | ≤ 1, that is, r ≤ 1, the scheme (2.14) satisfies the Von Neumann conditions, which is a necessary condition of the stability of the scheme (2.14). If r < 1, βh ≠ nπ, where n is an integer, then G has two different eigenvalues. If r < 1, βh = nπ, then G is an identity matrix, but (d/d_βh) G has two different eigenvalues [30]. So r < 1 is the sufficient condition of the stability for integrator (2.14). Note that, if r = 1, there is an unbounded solution

. So the scheme (2.14) is not stable when r = 1. Now, we find the necessary and sufficient condition of the stability for integrator (2.14), which is

(2.29)

With the consistence and stability conditions, we have following conclusion.

Theorem 2.2. The nonstandard finite difference variational integrator (2.14) is convergent, when the step sizes Δt and Δx satisfy ϕ(Δt) < ψ(Δx).

We have shown the idea of using the nonstandard finite difference method to get the discrete variational integrator and the corresponding discrete multisymplectic form formula. In the next section, we will consider the discrete variational integrators for a more complicated example, the nonlinear Klein-Gordon equation.

3. Nonstandard Finite Difference Variational Integrators for Nonlinear Klein-Gordon Equation

In this section, we consider the nonlinear Klein-Gordon equation [31],

(3.1)

As known, this equation can be obtained by Euler-Lagrange equation (2.2) with the Lagrangian function

(3.2)

Now we consider the triangle discretization and square discretization, respectively, to get the nonstandard finite difference variational integrators.

3.1. Triangle Discretization

Following the steps in last section and using the idea of nonstandard finite difference, we define the discrete Lagrangian L_d as

(3.3)

based on the following constructing rules,

(1)
The discrete first derivative is represented by
(3.4)
where the denominator functions are defined by (2.6), and
(3.5)
(2)
Nonlocal representations for u⁴ and u² are given by
(3.6)
where a₁, b₁, a₂, and b₂ are positive parameters. Such discretizations for u⁴ and u² guarantee the symmetric property of the discrete Lagrangian function [15].

Similarly, we define discrete Lagrangians on other two adjoint triangles,

(3.7)

Now, the discrete variational integrator with nonstandard finite difference methods could be obtained by discrete Euler-Lagrange equation (2.12):

(3.8)

Substituting

, and

into above equation, we arrive at

(3.9)

Using the definition of discrete Lagrangian functions, one can find that this scheme is symmetric with respect to (i, j + 1) and (i, j − 1), (i + 1, j) and (i − 1, j); that it is multisymplectic, and that it preserves the multisymplectic structure of the original equation.

Its corresponding discrete multisymplectic form formula can be obtained from (2.17), that is,

(3.10)

where

(3.11)

It shows the multisymplectic structure of scheme (3.9), and the relations between the field values on the three adjoint triangles are around .

We now analyze the truncation error of integrator (3.9). By Taylor series expansion [32, 33], we have

(3.12)

Combining the above two equations and (2.22), (2.23), we can observe that the nonstandard finite difference variational integrator (3.9) has the truncation error 𝒪((Δx) ² + ΔxΔt + (Δt) ²).

The above results are summarized in the following theorem.

Theorem 3.1. The nonstandard finite difference variational integrator (3.9) for the nonlinear Klein-Gordon equation (3.1) is multisymplectic, and its truncation error is 𝒪((Δx) ² + ΔxΔt + (Δt) ²). The discrete multisymplectic structure of this scheme is presented by (3.10).

3.2. Square Discretization

In this case, we denote a square at (i, j) with four ordered quaternion ((i, j), (i + 1, j), (i + 1, j + 1), and (i, j + 1)) by

and define X_□ to be the set of all such squares. Then the discrete jet bundle [6, 10] is defined as

(3.13)

which is equal to X_□ × ℝ⁴.

Following the philosophy of the nonstandard finite difference method, we define the discrete Lagrangian L_d on

(3.14)

In this case,

(1)
the discrete first-derivative is represented by
(3.15)
where the denominator functions are defined by (2.6), and
(3.16)
(2)
nonlocal representations for u⁴ and u² are
(3.17)

Similarly, we have the definitions of L_d on the other three squares adjoint to

(3.18)

Taking derivate of action functional with respect to

, we have the discrete Euler-Lagrange equation in this square discretization [5, 6, 10, 34], which is

(3.19)

Substituting the discrete Lagrangian

, and

into the previous equation, we arrive at

(3.20)

After simple calculations, it becomes

(3.21)

It is multisymplectic and symmetric in (i, j + 1) and (i, j − 1), (i + 1, j) and (i − 1, j). Similarly, we have the discrete multisymplectic form formula:

(3.22)

To study the truncation error of the integrator, we do the Taylor expansion which leads to

(3.23)

Combing these equations, we can readily observe that the nonstandard finite difference variational integrator (3.21) has truncation error 𝒪((Δx) ² + (Δt) ²). To verify this conclusion, we investigate the numerical convergence order in our numerical experiments. See Section 4.

We summarize our conclusion in the following theorem.

Theorem 3.2. The nonstandard finite difference variational integrator (3.21) for the nonlinear Klein-Gordon equation (3.1) is multisymplectic, and its truncation error is 𝒪((Δx) ² + (Δt) ²). The discrete multisymplectic structure of this scheme is presented by (3.22).

4. Numerical Simulations

In this section, we report the performance of the nonstandard finite difference variational integrator (2.14) for solving linear wave equation (2.1) and the nonstandard finite difference variational integrators (3.21) and (3.9) for the nonlinear Klein-Gordon equation (3.1).

4.1. Linear Wave Equation

For linear wave equation (2.1), we consider the initial conditions

(4.1)

and the periodic boundary conditions

(4.2)

The nonstandard finite difference variational integrator (2.14) is an explicit five points scheme. We choose the denominator functions ϕ and ψ in as ϕ(Δt) = 2sin (Δt/2) and ψ(Δt) = 2sin (Δx/2).

From Figure 1, we can see that the nonstandard finite difference variational integrator (2.14) for the linear wave equation performs very well and the periodicity of the linear wave equation is preserved accurately.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The waveforms of linear wave equation (2.1) by the nonstandard finite difference variational integrator (2.14) (Δt = 0.1, Δx = 0.2).

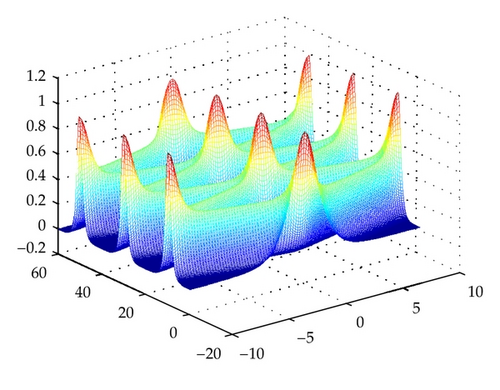
4.2. Nonlinear Klein-Gordon Equation

We now consider the nonlinear Klein-Gordon equation (3.1) with the initial condition

(4.3)

and periodic boundary conditions.

We use nonstandard finite difference variational integrator (3.21) to simulate this problem with amplitude A = 5. The nonstandard finite difference variational integrator (2.14) is an implicit nine-points nonstandard finite difference scheme. The denominator functions ϕ and ψ are defined the same as before.

As depicted in Figure 2, the nonstandard finite difference variational integrator (3.21) simulates the wave propagation perfectly at the beginning. After a long time simulation, the integrator still performs very accurate and stable, without showing any blowup. With periodic boundary condition, the wave going out the computational domain shows up in the other direction periodically.

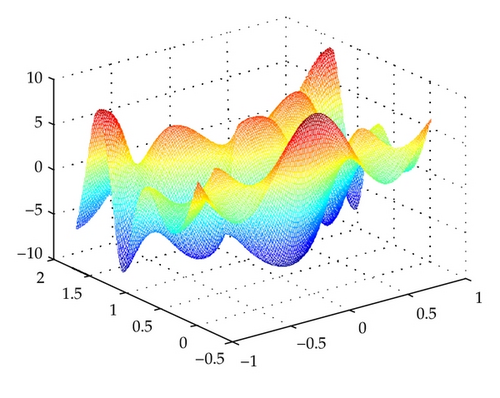
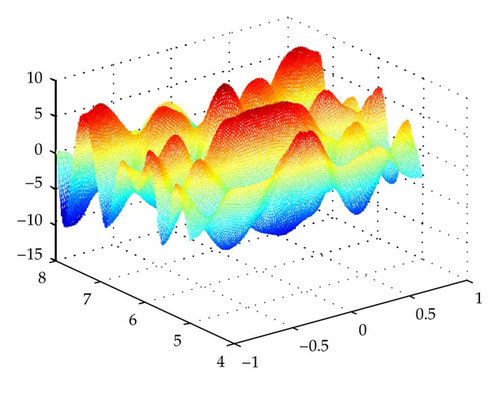
4.3. Convergence Order of the Nonlinear Integrators (3.9) and (3.21)

To further investigate the numerical convergence of the proposed schemes, we conduct a series of numerical tests of our nonlinear integrators. In this example, we consider the nonlinear Klein-Gordon equation (3.1) with the initial boundary conditions as follows:

(4.4)

where c = 1.2. The exact solution of the problem is

(4.5)

The nonstandard finite difference integrators (3.9) and (3.21) are applied to simulate the Klein-Gordon equation. In the integrator (3.9), we choose a₁ = b₁ = a₂ = b₂ = 1 here. The l^∞-norm errors at t = 1, t = 1.5, and t = 2 are listed in Tables 1 and 2. The orders in the tables are calculated with the formula [35, 36]

(4.6)

Table 1. The error and convergence orders of (3.9) for Klein-Gordon problem with Δt = Δx.

Mesh size	t = 1	t = 1.5	t = 2
Δx = 0.1
Error	6.3e − 3	8.9e − 3	1.07e − 2
Order	—	—	—

Δx = 0.05
Error	1.6e − 3	2.3e − 3	2.8e − 3
Order	1.9773	1.9522	1.9341

Δx = 0.025
Error	4.1645e − 4	5.8258e − 4	7.0059e − 4
Order	1.9419	1.9811	1.9988

Δx = 0.0125
Error	1.0480e − 4	1.4622e − 4	1.7565e − 4
Order	1.9905	1.9943	1.9959

Table 2. The error and convergence orders of (3.21) for Klein-Gordon problem with Δt = Δx.

Mesh size	t = 1	t = 1.5	t = 2
Δx = 0.1
Error	1.28e − 2	1.81e − 2	2.25e − 2
Order	—	—	—

Δx = 0.05
Error	3.3e − 3	4.6e − 3	5.7e − 3
Order	1.9556	1.9763	1.9809

Δx = 0.025
Error	8.3445e − 4	1.2e − 3	1.4e − 3
Order	1.9836	1.9386	2.0255

Δx = 0.0125
Error	2.0990e − 4	2.9458e − 4	3.6187e − 4
Order	1.9911	2.0263	1.9984

Overall, it is clear that the error decreases as the mesh size goes to zero, indicating the convergence of our nonlinear integrators (3.9) and (3.21). Moreover, numerical orders clearly exhibit second order convergence when the mesh size decreases with Δt = Δx, which further confirms our theoretical derivation of the truncation errors of the numerical schemes.

In all, the numerical tests verify that the nonstandard finite difference variational integrators that we developed are capable of preserving the characteristics of original equations. They are all accurate, effective, and suitable for solving multisymplectic systems.

5. Conclusion

In this paper, we have considered a linear wave equation and a nonlinear Klein-gordon equation. We have derived the nonstandard finite difference variational integrators and the corresponding multisymplectic form formulas from these two multisymplectic PDEs. We have shown that the nonstandard finite difference methods are flexible in constructing numerical schemes and can be employed to derive multisymiplectic schemes for multisymplectic systems. The convergence of our methods has been discussed. The numerical experiments have shown effectiveness and efficiency of these nonstandard finite difference variational integrators.

Acknowledgments

The authors are grateful to the editor and anonymous reviewers for their careful reading and many constructive suggestions which lead to a great improvement of this paper. This work is supported by the NNSF of China (no. 11271101) and the NNSF of Shandong Province (no. ZR2010AQ021).

References

1 Abraham R. and Marsden J. E., Foundations of Mechanics, 1978, 2nd edition, Benjamin/Cummings Publishing, Reading, Mass, USA, 515141, ZBL0454.62036.
Google Scholar
2 Chen J.-B., Variational integrators and the finite element method, Applied Mathematics and Computation. (2008) 196, no. 2, 941–958, https://doi.org/10.1016/j.amc.2007.07.028, 2388747, ZBL1135.65406.
10.1016/j.amc.2007.07.028
Web of Science® Google Scholar
3 Chen J.-B., Qin M.-Z., and Scherer R., Multisymplectic and variational integrators, International Journal of Pure and Applied Mathematics. (2008) 44, no. 4, 509–536, 2418209, ZBL1147.65103.
Google Scholar
4 Ciarlet P. G., Iserles A., Kohn R. V., and Wright M. H., Simulating Hamltonian Dynamics, 2004, Cambridge University Press, New York, NY, USA, Cambridge Monographs on Applied and Computational Mathematics.
Google Scholar
5 Marsden J. E. and West M., Discrete mechanics and variational integrators, Acta Numerica. (2001) 10, 357–514, https://doi.org/10.1017/S096249290100006X, 2009697, ZBL1123.37327.
10.1017/S096249290100006X
Google Scholar
6 Marsden J. E., Patrick G. W., and Shkoller S., Multisymplectic geometry, variational integrators, and nonlinear PDEs, Communications in Mathematical Physics. (1998) 199, no. 2, 351–395, https://doi.org/10.1007/s002200050505, 1666871, ZBL0951.70002.
10.1007/s002200050505
Web of Science® Google Scholar
7 Leok M. and Zhang J., Discrete Hamiltonian variational integrators, IMA Journal of Numerical Analysis. (2011) 31, no. 4, 1497–1532, https://doi.org/10.1093/imanum/drq027, 2846764, ZBL1232.65177.
10.1093/imanum/drq027
Web of Science® Google Scholar
8 Nawafleh K. I., Canonical quantization of higher-order Lagrangians, Journal of Applied Mathematics. (2011) 2011, 11, 375838, https://doi.org/10.1155/2011/375838, 2844122, ZBL1226.81098.
10.1155/2011/375838
Google Scholar
9 Pekarsky S. and Marsden J. E., Abstract mechanical connection and abelian reconstruction for almost Kähler manifolds, Journal of Applied Mathematics. (2001) 1, no. 1, 1–28, https://doi.org/10.1155/S1110757X01000043, 1844945, ZBL0998.53055.
10.1155/S1110757X01000043
Google Scholar
10 Vankerschaver J., Liao C., and Leok M., Generating functionals and Lagrangian PDEs, Journal of Nonlinear Science. In presshttps://doi.org/10.1080/00207161003743391.
10.1080/00207161003743391
Google Scholar
11 Mickens R. E., Applications of Nonstandard Finite Difference Schemes, 2000, World Scientific Publishing, Singapore, https://doi.org/10.1142/9789812813251, 1831401.
10.1142/4272
Google Scholar
12 Mickens R. E., Nonstandard finite difference schemes for differential equations, Journal of Difference Equations and Applications. (2002) 8, no. 9, 823–847, https://doi.org/10.1080/1023619021000000807, 1919887, ZBL1010.65032.
10.1080/1023619021000000807
Web of Science® Google Scholar
13 Mickens R. E., A nonstandard finite difference scheme for the diffusionless Burgers equation with logistic reaction, Mathematics and Computers in Simulation. (2003) 62, no. 1-2, 117–124, https://doi.org/10.1016/S0378%2D4754(02)00180%2D5, 1983580, ZBL1015.65036.
10.1016/S0378-4754(02)00180-5
Web of Science® Google Scholar
14 Mickens R. E., Dynamic consistency: a fundamental principle for constructing nonstandard finite difference schemes for differential equations, Journal of Difference Equations and Applications. (2005) 11, no. 7, 645–653, https://doi.org/10.1080/10236190412331334527, 2173250, ZBL1073.65552.
10.1080/10236190412331334527
Web of Science® Google Scholar
15 Mickens R. E., A numerical integration technique for conservative oscillators combining nonstandard finite-difference methods with a Hamilton′s principle, Journal of Sound and Vibration. (2005) 285, no. 1-2, 477–482, https://doi.org/10.1016/j.jsv.2004.09.027, 2213110, ZBL1237.70009.
10.1016/j.jsv.2004.09.027
Web of Science® Google Scholar
16 Arenas A. J., González-Parra G., and Chen-Charpentier B. M., A nonstandard numerical scheme of predictor-corrector type for epidemic models, Computers & Mathematics with Applications. (2010) 59, no. 12, 3740–3749, https://doi.org/10.1016/j.camwa.2010.04.006, 2651849, ZBL1198.65116.
10.1016/j.camwa.2010.04.006
Web of Science® Google Scholar
17 González-Parra G., Arenas A. J., and Chen-Charpentier B. M., Combination of nonstandard schemes and Richardson′s extrapolation to improve the numerical solution of population models, Mathematical and Computer Modelling. (2010) 52, no. 7-8, 1030–1036, https://doi.org/10.1016/j.mcm.2010.03.015, 2718414, ZBL1205.65015.
10.1016/j.mcm.2010.03.015
Google Scholar
18 Villanueva R. J., Arenas A. J., and Gonzlez-Parra G., A nonstandard dynamically consistent numerical scheme applied to obesity dynamics, Journal of Applied Mathematics. (2008) 2008, 14, 640154, https://doi.org/10.1155/2008/640154, ZBL1157.92028.
10.1155/2008/640154
Google Scholar
19 Jordan P. M., A nonstandard finite difference scheme for nonlinear heat transfer in a thin finite rod, Journal of Difference Equations and Applications. (2003) 9, no. 11, 1015–1021, https://doi.org/10.1080/1023619031000146922, 2027164, ZBL1037.65085.
10.1080/1023619031000146922
Web of Science® Google Scholar
20 Malek A., Applications of nonstandard finite difference methods to nonlinear heat transfer problems heat transfer-mathematical modelling, Numerical Methods and Information Technology In press.
Google Scholar
21 Ma Q., Ding D., and Ding X., A nonstandard fnite-difference method for a linear oscillator with additive noise, Applied Mathematics and Information Science. In presshttps://doi.org/10.1007/s002200050505.
10.1007/s002200050505
Google Scholar
22 Manning P. M. and Margrave G. F., Introduction to non-standard fnite-difference modelling, CREWES Research Report, 2006, no. 18.
Google Scholar
23 Bridges T. J., Multi-symplectic structures and wave propagation, Mathematical Proceedings of the Cambridge Philosophical Society. (1997) 121, no. 1, 147–190, https://doi.org/10.1017/S0305004196001429, 1418367, ZBL0892.35123.
10.1017/S0305004196001429
Web of Science® Google Scholar
24 Bridges T. J. and Reich S., Numerical methods for Hamiltonian PDEs, Journal of Physics A. (2006) 39, no. 19, 5287–5320, https://doi.org/10.1088/0305%2D4470/39/19/S02, 2220764, ZBL1090.65138.
10.1088/0305-4470/39/19/S02
Web of Science® Google Scholar
25 Bridges T. J. and Reich S., Multi-symplectic integrators: numerical schemes for Hamiltonian PDEs that conserve symplecticity, Physics Letters A. (2001) 284, no. 4-5, 184–193, https://doi.org/10.1016/S0375%2D9601(01)00294%2D8, 1854689, ZBL0984.37104.
10.1016/S0375-9601(01)00294-8
CAS Web of Science® Google Scholar
26 Hong J. and Liu Y., A novel numerical approach to simulating nonlinear Schrödinger equations with varying coefficients, Applied Mathematics Letters. (2003) 16, no. 5, 759–765, https://doi.org/10.1016/S0893%2D9659(03)00079%2DX, 1986047.
10.1016/S0893-9659(03)00079-X
Web of Science® Google Scholar
27 Hong J., Liu Y., Munthe-Kaas H., and Zanna A., Globally conservative properties and error estimation of a multi-symplectic scheme for Schrödinger equations with variable coefficients, Applied Numerical Mathematics. (2006) 56, no. 6, 814–843, https://doi.org/10.1016/j.apnum.2005.06.006, 2222122, ZBL1110.65116.
10.1016/j.apnum.2005.06.006
Web of Science® Google Scholar
28 Li X.-C. and Yao W.-A., Symplectic analytical solutions for the magnetoelectroelastic solids plane problem in rectangular domain, Journal of Applied Mathematics. (2011) 2011, 15, 165160, https://doi.org/10.1155/2011/165160, 2773956, ZBL1213.74135.
10.1155/2011/165160
Google Scholar
29 Vankerschaver J. and Leok M., A variational, second-order integrator for point vortices on the sphere. In presshttps://doi.org/10.1080/00207161003743391.
10.1080/00207161003743391
Google Scholar
30 Meis T. and Marcowitz U., Numerical Solution of Partial Differential Equations, 1981, Springer, Berlin, Germany, 617910.
10.1007/978-1-4612-5885-8
Google Scholar
31 El-Sayed A. M. A., Elsaid A., and Hammad D., A reliable treatment of homotopy perturbation method for solving the nonlinear klein-gordon equation of arbitrary (fractional) orders, Journal of Applied Mathematics. (2012) 2012, 13, https://doi.org/10.1155/2012/581481, 581481, ZBL1235.65148.
10.1155/2012/581481
Google Scholar
32 Chen J.-B., A multisymplectic integrator for the periodic nonlinear Schrödinger equation, Applied Mathematics and Computation. (2005) 170, no. 2, 1394–1417, https://doi.org/10.1016/j.amc.2005.01.031, 2175292, ZBL1103.65130.
10.1016/j.amc.2005.01.031
Web of Science® Google Scholar
33 Chen J.-B., Qin M.-Z., and Tang Y.-F., Symplectic and multi-symplectic methods for the nonlinear Schrödinger equation, Computers & Mathematics with Applications. (2002) 43, no. 8-9, 1095–1106, https://doi.org/10.1016/S0898%2D1221(02)80015%2D3, 1892487, ZBL1050.65127.
10.1016/S0898-1221(02)80015-3
Web of Science® Google Scholar
34 Leok M. and Shingel T., General techniques for constructing variational integrators, Frontiers of Mathematics in China. (2012) 7, no. 2, 273–303, https://doi.org/10.1007/s11464%2D012%2D0190%2D9, 2897705.
10.1007/s11464-012-0190-9
Web of Science® Google Scholar
35 Zhou S. and Cheng X., Numerical solution to coupled nonlinear Schrödinger equations on unbounded domains, Mathematics and Computers in Simulation. (2010) 80, no. 12, 2362–2373, https://doi.org/10.1016/j.matcom.2010.05.019, 2721184, ZBL1197.65162.
10.1016/j.matcom.2010.05.019
Web of Science® Google Scholar
36 Zhou S. and Cheng X., A linearly semi-implicit compact scheme for the Burgers-Huxley equation, International Journal of Computer Mathematics. (2011) 88, no. 4, 795–804, https://doi.org/10.1080/00207161003743391, 2774513, ZBL1213.65122.
10.1080/00207161003743391
Web of Science® Google Scholar

Citing Literature

All articles

Nonstandard Finite Difference Variational Integrators for Multisymplectic PDEs

Abstract

1. Introduction

1.1. Multisymplectic Structure of Discrete Variational Integrators

1.2. Nonstandard Finite Difference Methods

2. Nonstandard Finite Difference Variational Integrator for Linear Wave Equation