Journal of Applied Mathematics
Volume 2012, Issue 1 704138
Research Article
Open Access

Application of the Variational Iteration Method to Strongly Nonlinear q-Difference Equations

Hsuan-Ku Liu, 

Corresponding Author

Hsuan-Ku Liu

Department of Mathematics and Information Education, National Taipei University of Education, Taipei 106, Taiwan ntue.edu.tw

Search for more papers by this author
First published: 28 February 2012
https://doi.org/10.1155/2012/704138
Citations: 1
Academic Editor: Debasish Roy

Abstract

The theory of approximate solution lacks development in the area of nonlinear q-difference equations. One of the difficulties in developing a theory of series solutions for the homogeneous equations on time scales is that formulas for multiplication of two q-polynomials are not easily found. In this paper, the formula for the multiplication of two q-polynomials is presented. By applying the obtained results, we extend the use of the variational iteration method to nonlinear q-difference equations. The numerical results reveal that the proposed method is very effective and can be applied to other nonlinear q-difference equations.

1. Introduction

A time scale is a nonempty closed subset of real numbers. Recently, much research activity has focused on the theory and application of the q-calculus. For example, the q-calculus has being given a financial meaning by Muttel [1] and is applied to pricing the financial derivatives. Many real world problems are now formulated as q-difference equations. Nonlinear q-difference equations, as well as their analytic and numerical solutions, play an important role in various fields of science and engineering, especially in nonlinear physical science, since their solutions can provide more inside into the physical aspects of the problems.

Solutions of linear differential equations on time scales have been studies and published during the past two decades. One area lacking in development is the theory of approximate solutions on nonlinear q-difference equations. Recent developments in the theory of approximate solution have aroused further interest in the discussion of nonlinear q-difference equations.

One of the difficulties in developing a theory of series solutions for linear or nonlinear homogeneous equations on time scales is that formulas for multiplication of two generalized polynomials are not easily found. Haile and Hall [2] provided an exact formula for the multiplication of two generalized polynomials if the time scale had constant graininess. Using the obtained results, the series solutions for linear dynamic equations were proposed on the time scales ℝ and 𝕋 = hℤ (difference equations with step size h). For generalized time scales, Mozyrska and Pawtuszewicz [3] presented the formula for the multiplication of the generalized polynomials of degree one and degree n ∈ ℕ.

The variational iteration method proposed by He [4] has been proved by many authors to be a powerful mathematical tool for analysing the nonlinear problems on ℝ (the set of real numbers). The advantages of this method include (i) that it can be applied directly to all types of difference equations, and (ii) that it reduces the size of computational work while maintaining the high accuracy of the numerical solution. For the nonlinear q-difference equations, the approximate solution obtained by using the variational iteration method may not yet been found.

In this paper, we presented a formula for the multiplication of two q-polynomials. The obtained results can be used to find a series solution of the q-difference equations. The aim is to extend the use of the variational iteration method to strongly nonlinear q-difference equations. Precisely, the equation is described as
(1.1)
where xΔ = Δx/Δt is the q-derivative as defined in Definition 2.1. In future studies, we intend to extend the use of the variational iteration method to the other nonlinear q-difference equations.

This paper is organized as follows: in Section 2 basic ideas on q-calculus are introduced; in Section 3, the multiplication of two q-polynomials is demonstrated; in Section 4, the variational iteration method is applied to find an approximate solution of strongly nonlinear damped q-difference equations; in Section 5, the numerical results and the approximate solutions, which were very close, are presented; finally, a concise conclusion is provided in Section 6.

2. Introduction to q-Calculus

Let 0 < q < 1 and use the notations
(2.1)
where ℕ denotes the set of positive integers.
Let a and q be real numbers such that 0 < q < 1. The q-shift factorial [5] is defined by
(2.2)

Definition 2.1. Assume that is a function and . The q-derivative [6] at t is defined by

(2.3)

A q-difference equation is an equation that contains q-derivatives of a function defined on .

Definition 2.2. On the time scale , the q-polynomials are defined recursively as follows:

(2.4)
By computing the recurrence relation, the q-polynomials can be represented as
(2.5)
on qℕ [6].

Hence, for each fixed s, the delta derivative of hk with respect to t satisfies
(2.6)

Using q-polynomials, Agarwal and Bohner [7] gave a Taylor’s formula for functions on a general time scale. On Taylor’s formula is written follows.

Theorem 2.3. Let n ∈ ℕ. Suppose that f is n times differentiable on . Let . Then one has

(2.7)

3. Multiplication of Two q-Polynomials

The purpose of this section is to propose a production rule of two q-polynomials at 0 [8] which will be used to derive an approximate solution in the following section.

Theorem 3.1. Let hi(t, 0) and hj(t, 0) be two q-polynomials at zero. One has

(3.1)

Proof. Since

(3.2)
we have
(3.3)
This implies that
(3.4)

Proposition 3.2. Let hi(t, 0) and hj(t, 0) be any two q-polynomials. We have

(3.5)

Proof. By Theorem 3.1, it suffices to show that

(3.6)
Suppose i > j, one has
(3.7)

4. Variational Iteration Method

4.1. Basic Ideas of Variational Iteration Method

To clarify the ideas of the variational iteration method, we consider the following nonlinear equation:
(4.1)
where L is a linear operator, N is a nonlinear operator, and g is an inhomogeneous term. According to the variational iteration method, we can construct a correction functional as follows:
(4.2)
where λ is a general Lagrange multiplier, u0 is an initial approximation which must be chosen suitably, and is considered a restricted variation; that is, . To find the optimal value of λ, we make the above correction functional stationary with respect to xn, noticing that δxn(0) = 0, and have
(4.3)
Having obtained the optimal Lagrange multiplier, the successive approximations xn, n ≥ 0, of the solution x will be determined upon the initial function x0. Therefore, the exact solution is obtained at the limit of the resulting successive approximations.

4.2. Approximate Solution to Nonlinear Damped q-Equations

In this section, we extend the use of the variational iteration method to strongly nonlinear damped q-difference equation as follows:
(4.4)
with x(0) = a and xΔ(0) = b.
First of all, we illustrate the main idea of the variational iteration method. The basic character of the method is to construct a correction functional for the system (4.4), which reads
(4.5)
where L is a linear operator, N is a nonlinear operator, λ is a Lagrange multiplier which can be identified optimally by variational theory, xn is the nth approximation, and denotes a restricted variation, that is, .
In this work, the linear operator L is selected as
(4.6)
and the nonlinear operator N is selected as
(4.7)
Making the above correction functional stationary with respect to xn
(4.8)
we, therefore, have the following stationary conditions:
(4.9)
The Lagrange multiplier can be readily identified:
(4.10)
As a result, we obtain the variational iteration formula:
(4.11)
According to the initial condition, we begin with the following initial approximation:
(4.12)
According to the variational iteration formula, we have
(4.13)
where
(4.14)
and H(i, j) = (qi+1; q) j/(q; q) j.

5. Numerical Method

By Definition 2.1, the derivative of x(t) at 0 is defined as
(5.1)
Let N0 > 0 be a nonnegative integer. To obtain an approximation for the derivative of x(t) at t = 0, we use
(5.2)
Rearrangement leads to
(5.3)
where the dominant term in the truncation error is .
Since xΔ(0) = b, we have
(5.4)
which yields
(5.5)
Set t0 = 0 and and define
(5.6)
Then the interval [0, q] is partitioned into N0 subintervals.
Now we denote
(5.7)
The Delta-derivative of x(t) at ti can be calculated as
(5.8)
where
(5.9)
Substituting (5.8) into (4.4) yields the following:
(5.10)
This implies that
(5.11)

6. Numerical Results

The theoretical considerations introduced in previous sections are illustrated with examples, where the approximate solutions are compared with the numerical solutions.

The time scale is given as {0.9n∣n ∈ ℕ}∪{0} = {0.9,0.81,0.729, …, 0}, where 0 is the cluster point of . For the numerical computations, the interval [0,0.9] is partitioned into 100 subintervals. The maximum error and the average error are defined as
(6.1)
respectively, where is the approximate solution with n iterations and is the numerical solution obtained by (5.11).

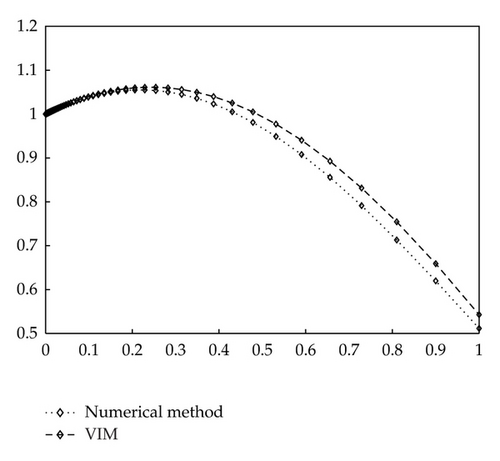
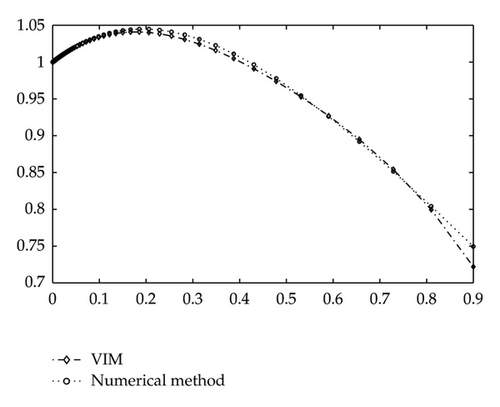
Example 6.1. Consider the underdamped cases with (i) 2γ = 0.1, γ1 = 0.1, ε = 1, and Ω = 1; and (ii) 2γ = 0.1, γ1 = 2.5, ε = 1 and Ω = 1. As the initial conditions are given as x(0) = 1 and xΔ(0) = 0.5, we begin with the initial approximation x0 = 1 + 0.5t. By the variational iteration formula (4.11), we obtain the first few components of xn(t). In the same manner the rest of the components of the iteration formula are obtained using the symbolic toolbox in the Matlab package.

For Case (i) The first two components of xn are obtained as

(6.2)
and so on. After 3 iterations, the maximum error is 0.0415 and the average error is 0.00356.

For case (ii) The first two components of xn are obtained as

(6.3)
and so on. After 3 iterations, the maximum error is 0.0275 and the average error is 0.001167.

The responses of x(t) are shown in Figures 1 and 2 for cases (i) and (ii), respectively.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Time response for xΔΔ + (0.1 + 0.1x)xΔ + x + x2 = 0 with 3 iterations.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Time response for xΔΔ + (0.1 + 2.5x)xΔ + x + x2 = 0 with 3 iterations.

Example 6.2. In this example, we consider the overdamped cases with (iii) 2γ = 2.5, γ1 = 0.1, ε = 1, and Ω = 1; and (iv) 2γ = 2.5, γ1 = 2.5, ε = 1, and Ω = 1. As the initial conditions are given as x(0) = 1 and xΔ(0) = 0.5, we begin with the initial approximation x0 = 1 + 0.5t. By the variational iteration formula (4.11), we obtain the first few components of xn(t). In the same manner the rest of the components of the iteration formula were obtained using the symbolic toolbox in the Matlab package.

For Case (iii) The first two components of xn are obtained as

(6.4)
and so on. After 3 iterations, the maximum error is 0.01609 and the average error is 0.001227.

For Case (iv) The first two components of xn are obtained as

(6.5)
and so on. After 7 iterations, the maximum error is 0.026 and the average error is 0.00105. At less than 7 iterations, the approximate solution is not close to the numerical solution.

The responses of x(t) are shown in Figures 3 and 4 for cases (iii) and (iv), respectively.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Time response for xΔΔ + (2.5 + 0.1x)xΔ + x + x2 = 0 with 3 iterations.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Time response for xΔΔ + (2.5 + 2.5x)xΔ + x + x2 = 0 with 7 iterations.

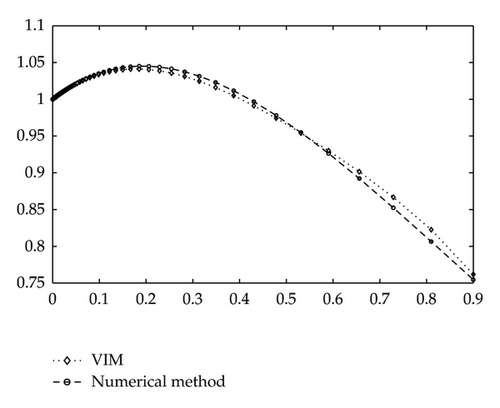
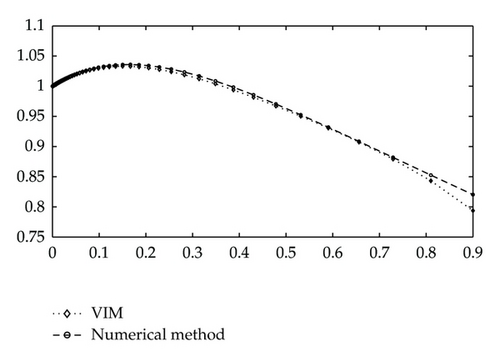
These figures and the maximum/average errors indicate that the approximate solution is close to the numerical results.

7. Conclusion

In the area of q-calculus, the formula for the multiplication of two q-polynomials has long been in need of development. In this paper, we have presented the aforementioned formula, overcoming the previous difficulties in developing a theory of series solutions for the nonlinear q-difference equations. The goal of this paper was to extend the use of the variational iteration method to strongly nonlinear damped q-difference equations. The numerical results have demonstrated that the approximate solution obtained by the variational iteration method is very accurate. Therefore, the proposed method is very effective and can be applied to other nonlinear q-equations.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.