The problem of magnetomicropolar fluid flow, heat, and mass transfer with suction through a porous medium is numerically analyzed. The problem was studied under the effects of chemical reaction, Hall, ion-slip currents, and variable thermal diffusivity. The governing fundamental conservation equations of mass, momentum, angular momentum, energy, and concentration are converted into a system of nonlinear ordinary differential equations by means of similarity transformation. The resulting system of coupled nonlinear ordinary differential equations is the then solved using a fairly new technique known as the successive linearization method together with the Chebyshev collocation method. A parametric study illustrating the influence of the magnetic strength, Hall and ion-slip currents, Eckert number, chemical reaction and permeability on the Nusselt and Sherwood numbers, skin friction coefficients, velocities, temperature, and concentration was carried out.

1. Introduction

Eringen [1] proposed the theory of micropolar fluids, which shows microrotation effects as well as microinertia, as these flow properties cannot be described by the classical Navier-Stokes theory. Since the pioneering work by Eringen, the theory of micropolar fluid has generated a lot of interest. Extension has been done, to include studies of magneto-micropolar fluid with Hall current and ion-slip currents with heat transfer due to vast possible engineering applications in areas like power generators, MHD accelerators, refrigeration coils, electric transformers, and heating elements. MHD flows of a viscous and incompressible fluid have been extensively studied with the effect of Hall current by Chamkha [2], Seddeek [3], Takhar et al. [4], Shateyi et al. [5, 6], Salem and Abd El-aziz [7], among others.

The momentum, heat, and mass transport on stretching sheet has several applications in polymer processing as well as in electrochemistry. The heat transfer problem associated with the boundary layer micropolar fluid under different physical conditions has been studied by several authors. Takhar et al. [8] considered diffusion of a chemical reactive species from a stretching sheet. Muthucumaraswamy and Ganesan [9] studied diffusion and first-order chemical reaction on impulsively started infinite vertical plate with variable temperature. Shateyi [10] investigated thermal radiation and buoyancy effects on heat and mass transfer over a semi-infinite stretching sheet with suction and blowing. Shateyi and Motsa [11] numerically investigated the unsteady heat, mass, and fluid transfer over a horizontal stretching sheet.

The porous media heat and mass transfer problems have several practical engineering applications such as geothermal systems, crude oil extraction, and ground-water pollution. The study of chemical reaction heat transfer in porous medium has important applications such as in tabular reactors, oxidation of solid materials, and synthesis of ceramic materials. Elgazery [12] numerically analyzed the effects of chemical reaction, Hall, ion-slip currents, variable viscosity and variable thermal diffusivity on the problem of magnetomicropolar fluid flow, heat and mass transfer with suction and blowing through a porous medium. Srinivasacharya and RamReddy [13] presented natural convection heat and mass transfer along a vertical plate embedded in a doubly stratified micropolar fluid saturated non-Darcy porous medium. Ishak et al. [14] investigated the unsteady boundary layer flow over a stretching permeable surface.

Elshehawey et al. [15] applied the Chebyshev finite-difference method to investigate the effects of Hall and ion-slip currents on magneto-hydrodynamic flow with variable thermal conductivity. Seddeek and Salama [16]. studied effects of chemical reaction and variable viscosity on hydromagnetic mixed convection heat and mass transfer for Hiemenz flow through porous media with radiation. Shateyi and Motsa [17] analyzed numerically the problem of magnetohydrodynamic flow and heat transfer of a viscous, incompressible and electrically conducting fluid past a semi-infinite unsteady stretching sheet with Hall currents, variable viscosity and thermal diffusivity. Mahmoud and Waheed [18] performed a theoretical analysis to study heat transfer characteristics of magnetohydrodynamic mixed convection flow of a micropolar fluid past a stretching surface with slip velocity at the surface and heat generation/absorption.

The aim of this work is to analyze the effects of chemical reaction, Hall and ion-slip currents on the MHD flow of a micropolar fluid through a porous medium using the successive linearization method (SLM). The SLM is based on a novel idea of iteratively linearizing the underlying governing nonlinear equations, which are written in similarity form, and solving the resulting equations using spectral methods. This approach has been successfully applied to different flow problem (see, e.g., Makukula et al. [19–22]; Shateyi and Motsa [17]; Motsa and Shateyi [23, 24]). The influences of the governing parameters on the flow characteristics are illustrated graphically and using tables.

2. Problem Formulation

We consider a steady, incompressible, magneto-micropolar and electrically conducting viscous fluid flowing over a horizontal plate in the x-direction under the influence of mass transfer with chemical reaction through a porous medium. We let the reaction of a species, say A with B be the first order homogeneous chemical reaction with a constant rate, κ. We also assume that the concentration of dissolved A is small enough and physical properties ρ and D are virtually constant throughout the fluid. The flow under consideration is also subjected to a strong transverse magnetic field B₀ with a constant intensity along the y-axis (see Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The physical configuration and coordinate system for the boundary layer flow.

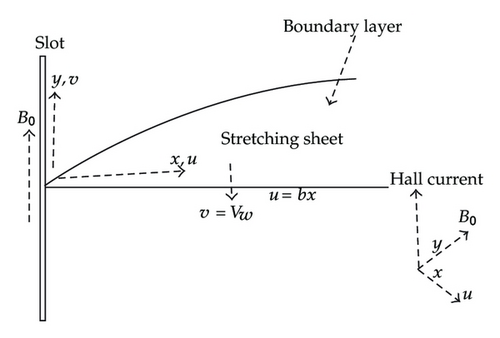
Generally, an electrically conducting fluid is affected by Hall and ion-slip currents in the presence of a magnetic field. The effect of Hall current gives rise to a force in the z-direction, which induces a cross-flow in the z-direction and hence the flow becomes three-dimensional.

Following Elgazery [12], the generalized Ohms law including Hall currents is given by

(2.1)

where σ is the electrical conductivity, J = (J_x, J_y, J_z) is the electric current vector, V is the velocity vector, E is the intensity of the electric field, B is the magnetic induction vector, 1/en_e is the Hall factor, ω/ν_e is the Hall parameter, n_e is the density number of the electrons, e is the charge of electron, ν_e is the electron-atom collision frequency and ω exceeds the collision frequency. The electric magnetic field can force both the ions and electrons to produce a relative drift between them and neutral particles, when the ratio, ω/ν_e becomes very large. The drift is called “ion-slip” and is however negligible for highly ionized gases.

We assume that all the fluid properties are isotropic and constant. The velocity component u on a stretching sheet is proportional to its distance from the slit. Under the usual boundary layer and Boussinesq approximations, the governing equation in (x, y, z)-coordinate for the problem under consideration can be written as follows:

(2.2)

(2.3)

(2.4)

(2.5)

(2.6)

(2.7)

The boundary conditions are

(2.8)

Here (u, v, w) are the fluid velocity components in the (x, y, z)-directions, respectively. ρ is the fluid density, μ is the dynamic viscosity, c_p the specific heat at constant pressure, β_t the coefficient of thermal expansion, β_c the coefficient of concentration expansion, U_∞, T_∞ and C_∞ the fluid free stream velocity, temperature, and concentration, respectively, N is the component of microrotation of the fluid, K is the vortex viscosity, G₁ is the spin gradient viscosity. and k^* permeability of the porous medium. β_e and β_i are respectively, the Hall parameter and the ion-slip parameter, where α_e = 1 + β_iβ_e. b is a constant with dimension (time) ⁻¹. U_s is the surface velocity and V_w is suction/injection velocity, ν is the kinematic viscosity, D is the chemical molecular diffusivity, α is the thermal diffusivity, k is the chemical reaction, and B₀ is the magnetic field of constant strength.

The governing differential equations (2.2)–(2.7) together with the boundary conditions (2.8) are non-dimensionalised using the following similarity transformations:

(2.9)

where f(η), g(η), h(η), θ and ϕ(η) are the dimensionless stream function and microrotation functions, temperature, and concentration distributions functions, respectively. η is the similarity variable. The variation of thermal diffusivity with the dimensionless temperature is written in the form:

(2.10)

where β₂ is parameter depending on the nature of the fluid, and α₀ is the thermal diffusivity of the fluid at temperature T_w. Then introducing the relations (2.9) into the equations (2.3)–(2.7) respectively, we obtain the following local similarity equations:

(2.11)

(2.12)

(2.13)

(2.14)

(2.15)

where the primes denote differentiation with respect to

is the magnetic parameter, N₁ = K/ρν is the coupling constant parameter, G = G₁b/Kν is the microrotation parameter, Pr = ν/α is the Prandtl number, Sc = ν/D is the Schmidt number,

is the Eckert number, k_p = k^*b/μ₀ is the permeability parameter, Re = xU_s/ν₀, is the Reynolds number,

is the nondimensional chemical reaction parameter. In view of the similarity transformations, the boundary conditions transform into:

(2.16)

where

is the mass transfer coefficient such that f_w > 0 indicates suction and f_w < 0 indicates blowing at the surface.

For practical applications, quantities of interest include the velocity components u and w, temperature and concentration, the local skin friction coefficients

and

, the local Nusselt number

, and the local Sherwood number

, where τ_w = [(μ+K)(∂u/∂y)+KN]_y=0 and τ_z = [(μ+K)(∂w/∂y)]_y=0 are the shear stress at the wall. By using (2.9), these quantities can be expressed as:

(2.17)

3. Generalization of the Successive Linearisation Method (SLM)

In this section we describe the basic idea behind the proposed method of successive linearisation method (SLM) and we derive formulas that can be used to implement the generalized SLM in any system of nonlinear boundary value problems. We consider a general n-order nonlinear system of ordinary differential equations which is represented by the nonlinear boundary value problem of the form

(3.1)

where Y(x) is a vector of unknown functions, x is an independent variable, and the primes denote ordinary differentiation with respect to x. The functions L and N are vector functions which represent the linear and nonlinear components of the governing system of equations, respectively, defined by

(3.2)

where y₁, y₂, …, y_k are the unknown functions. We define an initial guess Y₀(x) of the solution of (3.1) as

(3.3)

For illustrative purposes, we assume that (3.1) is to be solved for x ∈ [a, b] subject to the boundary conditions

(3.4)

where Y_a and Y_b are given constants. In previous implementation of the SLM (see, e.g., [19–25]) an appropriate initial guess was considered to be functions that satisfy the governing boundary conditions of (3.1). The general approach proposed in this study assumes that the initial approximation is a solution of the equation

(3.5)

which is solved subject to the underlying problem’s boundary conditions.

Define a function Z₁(x) to represent the vertical difference between Y(x) and the initial guess Y₀(x), that is,

(3.6)

For example, the vertical displacement between the variable y₁(x) and its corresponding initial guess y_1,0(x) is z_1,1 = y₁(x) − y_1,0(x). This is shown in Figure 2.

Substituting (3.6) in (3.1) gives

(3.7)

Since Y₀(x) is an known function, solving (3.7) would yield an exact solution for Z₁(x). However, since the equation is nonlinear, it may not be possible to find an exact solution. We therefore look for an approximate solution which is obtained by solving the linear part of the equation assuming that Z₁ and its derivatives are small. This assumption enables us to use the Taylor series method to linearise the equation. If Z₁(x) is the solution of the full equation (3.7) we let Y₁(x) denote the solution of the linearised version of (3.7). Expanding (3.7) using Taylor series (assuming Z₁(x) ≈ Y₁(x)) and neglecting higher order terms gives

(3.8)

The partial derivatives inside square brackets in (3.8) represent Jacobian matrices of size k × k, defined as

(3.9)

where i = 1 and p is the order of the derivatives.

Since the right hand side of (3.8) is known and the left hand side is linear, the equation can be solved for Y₁(x). Assuming that the solution of the linear part (3.8) is close to the solution of (3.7), that is, Z₁(x) ≈ Y₁(x), the current estimate (1st order) of the solution Y(x) is

(3.10)

To improve on this solution, we define a slack function, Z₂(x), which when added to Y₁(x) gives Z₁(x) (see, e.g., Figure 3), that is

(3.11)

Since Y₁(x) is now known (as a solution of (3.8) ), we substitute (3.11) in (3.7) to obtain

(3.12)

Solving (3.12) would result in an exact solution for Z₂(x). But since the equation is nonlinear, it may not be possible to find an exact solution. We therefore linearise the equation using Taylor series expansion and solve the resulting linear equation. We denote the solution of the linear version of (3.12) by Y₂(x), such that Z₂(x) ≈ Y₂(x). Setting Z₂(x) = Y₂(x) and expanding (3.12), for small Y₂(x) and its derivatives gives

(3.13)

where the partial derivatives inside square brackets in (3.13) represent Jacobian matrices defined as in (3.9) with i = 2.

After solving (3.13), the current (2nd-order) estimate of the solution Y(x) is

(3.14)

Next we define Z₃(x) (see Figure 4) such that

(3.15)

Equation (3.15) is substituted in the nonlinear (3.12) and the linearisation process described above is repeated. This process is repeated for m = 3,4, 5, …, i. In general, we have

(3.16)

Thus, Y(x) is obtained as

(3.17)

The procedure for obtaining each Z_i(x) is illustrated in Figures 2, 3, and 4, respectively, for i = 1,2, 3.

We note that when i becomes large, Z_i+1 becomes increasingly smaller. Thus, for large i, we can approximate the ith-order solution of Y(x) by

(3.18)

Starting from a known initial guess Y₀(x), the solutions for Y_i(x) can be obtained by successively linearising the governing equation (3.1) and solving the resulting linear equation for Y_i(x) given that the previous guess Y_i−1(x) is known. The general form of the linearised equation that is successively solved for Y_i(x) is given by

(3.19)

where

(3.20)

4. Numerical Solution

In this section we solve the governing (2.11)–(2.15) using the SLM method described in the last section. We note that (2.11)–(2.13) can be solved independently of equations (2.14)–(2.15). We begin by using the SLM approach to solve for f, g and h. We write the governing equations (2.11)–(2.13) as a sum of the linear and nonlinear components as

(4.1)

where the primes denote differentiation with respect to η and

(4.2)

Using (3.19), the general equation to be solved for Y_i, where

(4.3)

(4.4)

subject to the boundary conditions

(4.5)

where

(4.6)

and the sums in (4.6) denote

. Once each solution for f_i, g_i, h_i (i ≥ 1) has been found from iteratively solving equations (4.4)–(4.5), the approximate solutions for f(η), g(η), and h(η) are obtained as

(4.7)

where i is the order of SLM approximation. Since the coefficient parameters and the right hand side of (4.4)), for i = 1,2, 3, …, are known (from previous iterations). The equation system is solved using the Chebyshev spectral collocation method. This method is based on approximating the unknown functions by the Chebyshev interpolating polynomials in such a way that they are collocated at the Gauss-Lobatto points defined as

(4.8)

where N + 1 is the number of collocation points used (see, e.g., [26–28]). In order to implement the method, the physical region [0, ∞) is transformed into the region [−1,1] using the domain truncation technique in which the problem is solved on the interval [0, L] instead of [0, ∞). This leads to the mapping

(4.9)

where L is the scaling parameter used to invoke the boundary condition at infinity. The unknown functions f_i, θ_i and ϕ_i are approximated at the collocation points by

(4.10)

where T_k is the kth Chebyshev polynomial defined as

(4.11)

The derivatives of the variables at the collocation points are represented as

(4.12)

where a is the order of differentiation and D = (2/L)D with D being the Chebyshev spectral differentiation matrix (see, e.g., [26, 28]). Substituting (4.9)–(4.12) in (4.4))–((4.5) leads to the matrix equation given as

(4.13)

subject to the boundary conditions

(4.14)

where

(4.15)

(4.16)

(4.17)

and Y_i and R_i−1 are (3N + 1) × 1 column vectors defined by

(4.18)

where

(4.19)

In the above definitions, a_k,i−1, (k = 1,2, 3) are now diagonal matrices of size 3(N + 1) × 3(N + 1) and the superscript T is the transpose.

To impose the boundary conditions (4.14) on (4.13) we begin by splitting the matrix M in (4.13) into 9 blocks each of size (N + 1)×(N + 1) in such a way that M takes the form

(4.20)

We then modify the first and last rows of M_mn (m, n = 1,2, 3) and r_m,i−1 and the N − 1th row of M_1,1, M_1,2, M_1,3 in such a way that the modified matrices M_i−1 and R_i−1 take the form

(4.21)

After modifying the matrix system (4.13) to incorporate boundary conditions, the solution is obtained as

(4.22)

We use (3.5) to solve solve for the initial approximation Y₀. If we use the Chebyshev spectral method to solve for Y₀, we arrive at the following:

(4.23)

subject to the boundary conditions

(4.24)

where A is as defined in (4.16) and Y₀ are (3N + 1) × 1 column vectors defined by

(4.25)

where

(4.26)

To impose the boundary conditions (4.24) on the system (4.23) we begin by splitting the matrix A into 9 blocks each of size (N + 1)×(N + 1) in such a way that A takes the form

(4.27)

We then modify the first and last rows of A_mn (m, n = 1,2, 3) and the N − 1th row of A_1,1, A_1,2, A_1,3 in such a way that the modified matrix A takes the form;

(4.28)

We introduce a matrix R₀ on the right hand side of (4.23) such that

(4.29)

where

(4.30)

The solution Y₀ is obtained as

(4.31)

Thus, starting from Y₀, the solutions for Y_i are then obtained iteratively from solving equation (4.22). Once the solution for f and g and h have been obtained, the solutions for θ and ϕ can be found using the same procedure as described above.

5. Results and Discussion

In this section, we present the results obtained using both the successive linearization method and Chebyshev spectral collocation numerical method. The number of collocation points employed in this investigation is N = 50. The results are also validated against those obtained using the Matlab built-in solver bvp4c as well as reported by Elgazery [12]. Table 1 represents comparison between the SLM, Chebyshev pseudospectral method [12], and the bvp4c results of the local Nusselt number −θ^′(0). We note from this table that the SLM and the bvp4c results match exactly but the results reported by Elgazery [12] are slightly different from the current results. This is an interesting observation, since Elgazery [12] also applied the pseudospectral method, this substantiate the claim that the SLM technique improves the accuracy of the Chebyshev method. We also note in this table that the absolute values of the Nusselt number decrease with increasing values of magnetic parameter and the ion-slip parameter. However, it increases with increasing values of the Hall parameter.

Table 1. Comparison of the present results (4th-order) for the local Nusselt number −θ^′(0) against the bvp4c results and the results of [12] for various values of β_e, β_i and M at Pr = 0.72, β₂ = 0.5, f_w = 0.1, k_p = 2, Re = 1, G = 2, N₁ = 0.2, and Ec = 0.02.

M	β_e	β_i	[12]	Present	bvp4c
0	5	0.4	0.327498	0.32749528	0.32749528
0.5			0.324844	0.32484164	0.32484164
1			0.321912	0.32190912	0.32190912
1.5			0.318772	0.31876809	0.31876809

0.3	0		0.311234	0.31122885	0.31122885
	1		0.319297	0.31929392	0.31929392
	2		0.323083	0.32308061	0.32308061

0.3	5	0	0.326696	0.32669328	0.32669328
		0.2	0.326225	0.32622274	0.32622274
		0.5	0.325865	0.32586231	0.32586231

Table 2 gives the results of the wall stresses (C_fx) for various values of k_p, N₁, β_e, and β_i when other parameters are fixed. For fixed values of N₁, we observe that the absolute values of the local-skin friction decrease with the increasing values of the permeability parameter (k_p). The local shear stress (C_fx) increases in absolute values as the coupling parameter increases. The local wall shear stress (C_fx) increases in absolute values when the Hall parameter or ion-slip parameter increases.

Table 2. The wall shear stresses C_fx = (1 + N₁)f^′′(0) for various values of k_p, N₁, β_e, and β_i at M = 0.3, Pr = 0.72, f_w = 0.1, Re = 1, G = 2, and Ec = 0.02.

k_p	N₁	β_e	β_i	2nd-Order	3rd-Order	4th-Order	6th-Order
0.1	1	5	0.4	−6.65334091	−6.65334091	−6.65334091	−6.65334091
0.5	1	5	0.4	−3.46988916	−3.46989224	−3.46989224	−3.46989224
1	1	5	0.4	−2.83779413	−2.83787814	−2.83787815	−2.83787815
2	1	5	0.4	−2.46510143	−2.46622986	−2.4662317	−2.4662317

2	0.1	5	0.4	−1.40914015	−1.40961763	−1.40961811	−1.40961811
2	0.5	5	0.4	−1.88961638	−1.89034144	−1.89034233	−1.89034233
2	1	5	0.4	−2.46510143	−2.46622986	−2.4662317	−2.4662317
2	2	5	0.4	−3.52816005	−3.53067494	−3.53068356	−3.53068356

2	0.5	0	0.4	−2.04791788	−2.04807626	−2.04807629	−2.04807629
2	0.5	2	0.4	−1.91920286	−1.91972357	−1.91972398	−1.91972398
2	0.5	4	0.4	−1.89445825	−1.89514419	−1.89514497	−1.89514497
2	0.5	6	0.4	−1.88649265	−1.88724415	−1.88724512	−1.88724512

2	0.5	5	0	−1.88077116	−1.88155788	−1.88155895	−1.88155895
2	0.5	5	2	−1.88698782	−1.88774243	−1.88774341	−1.88774341
2	0.5	5	4	−1.8814535	−1.88225343	−1.88225455	−1.88225455
2	0.5	5	6	−1.8789626	−1.87978367	−1.87978486	−1.87978486

The values of the wall shear stresses (C_fx, C_fz), the local Nusselt number −θ^′(0) and the local Sherwood number −ϕ^′(0) for different Hartman number M, Hall parameter β_e, ion-slip parameter β_i, and coupling parameter N₁ are presented in Table 3. It is observed in this table that the local skin-friction coefficients f^′′(0) and g^′(0) increase with increasing values of M and N₁ but g^′(0) decreases as values of β_e and β_i increase. Both the local Nusselt number and the Sherwood number are found to be decreasing with increasing values of the Hartman number M and they also slightly decrease with increasing values of the ion-slip parameter and the coupling parameter. The local Nusselt number and the Sherwood number increases as Hall currents increase.

Table 3. The local Nusselt number −θ^′(0), Sherwood number −ϕ^′(0), and the wall shear stresses C_fx = (1 + N₁)f^′′(0) and C_fz = (1 + N₁)g^′(0) for various values of β_e, β_i, M and N₁ at Pr = 0.72, f_w = 0.1, k_p = 2, Re = 1, G = 2 and Ec = 0.02.

M	β_e	β_i	N₁	C_fx	C_fz	−θ′(0)	−ϕ^′(0)
1	5	0.4	0.2	−1.56322914	0.08599136	0.32190912	0.48724548
2	5	0.4	0.2	−1.61077402	0.16422572	0.31547847	0.48232094
3	5	0.4	0.2	−1.65972336	0.23554336	0.30864336	0.47715106
4	5	0.4	0.2	−1.70922564	0.3008927	0.30169844	0.47195166
5	5	0.4	0.2	−1.75872895	0.3611565	0.29482895	0.4668536

0.3	0	0.4	0.2	−1.65812419	0	0.31122885	0.47941184
0.3	2	0.4	0.2	−1.55508122	0.04885996	0.32308061	0.48818323
0.3	4	0.4	0.2	−1.53530214	0.03171899	0.32547247	0.49001302
0.3	6	0.4	0.2	−1.52894206	0.02291991	0.32624205	0.49060833

0.3	5	0	0.2	−1.52437745	0.03510497	0.32669328	0.49098971
0.3	5	0.5	0.2	−1.53222519	0.02430318	0.32586231	0.49030887
0.3	5	1	0.2	−1.53273738	0.01483309	0.32583913	0.49027923
0.3	5	1.5	0.2	−1.53110355	0.00931987	0.32603778	0.49043266

0.3	5	0.5	0	−1.28738139	0.02038592	0.32757864	0.49138014
0.3	5	0.5	0.2	−1.53222519	0.02430318	0.32586231	0.49030887
0.3	5	0.5	0.5	−1.89132586	0.03006273	0.32307538	0.48858611
0.3	5	0.5	1	−2.46753529	0.03931368	0.31775592	0.48535366

Graphical representation of the numerical results are illustrated in Figure 5 through Figure 13 to depict the influence of different parameters on the flow characteristics. Figure 5 depicts the effects of the Hall current parameter β_e on the velocity components f^′(η) and g(η). We see that the stream velocity profiles f^′(η) increases as β_e increases. We also observe in this figure that velocity distribution across the stretching sheet g(η) increases with increasing values of β_e when β_e ≤ 1 but decreases with increasing values of β_e greater than unity.

Description unavailable — **Figure 5 (a)**
Open in figure viewer PowerPoint

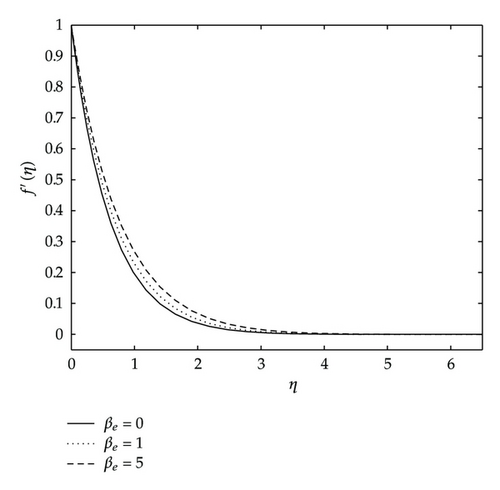
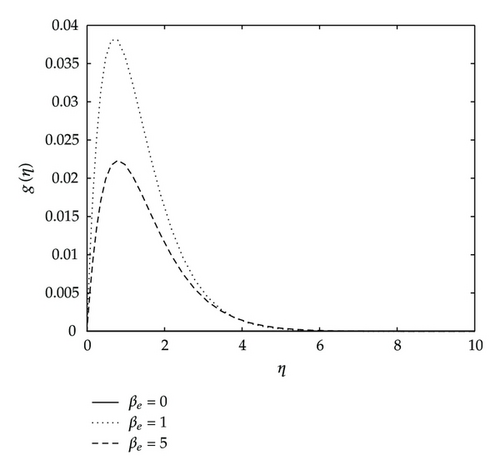
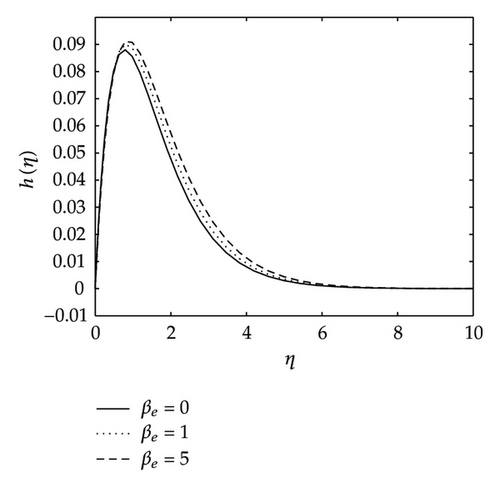
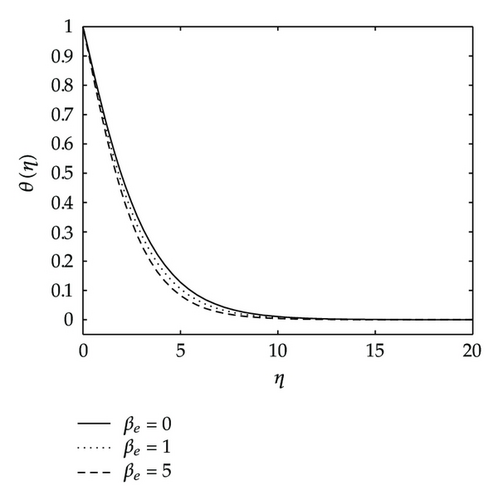
Figure 6 depicts the effects of the Hall current parameter β_e on the angular velocity h(η), temperature and concentration distributions. We observe that the angular velocity steeply rises up to maximum peaks as the Hall parameter increases. In the same figure we see that both the temperature and concentration profiles approach their classical values when the Hall parameter β_e becomes large. They both decrease with increasing values of β_e.

The influence of the Hartman number on the stream velocity and the velocity across the plate is depicted in Figure 7. It is observed that the stream velocity of the fluid decreases with the increase of the magnetic field parameter values. The decrease in this velocity component as the Hartman number (M) increases is because the presence of a magnetic field in an electrically conducting fluid introduces a force called the Lorentz force, which acts against the flow if the magnetic field is applied in the normal direction, as in the present study. This resistive force slows down the fluid velocity component as shown in Figure 7. In Figure 7 we have the influence of the magnetic field parameter on the lateral velocity. It can be seen that as the values of this parameter increase, the lateral velocity increases.

Figure 8 shows the effects of the magnetic parameter M on the angular velocity h(η), temperature and concentration profiles. As expected, the angular velocity steeply increases with every value of the magnetic value until attaining a peak and thereafter the angular velocity decreases monotonically with increasing values of M. In this figure, we also observe that both the temperature and concentration boundary layers become thick as values of the magnetic parameter increase. The effects of a transverse give rise to a resistive-type force called the Lorentz force. This force has the tendency to slow down the motion of the fluid and increase its thermal and concentration boundary layers hence increasing the temperature and concentration fields of the flow.

Figures 9 and 10 give the effects of the permeability parameter k_p on the velocity components, temperature and concentration distributions. As shown in these figures, all the velocity components are increasing with increasing values of the permeability parameter, whereas the temperature and concentration decrease as the permeability parameter k_p increases. Physically, this means that the porous medium impact on the boundary layer growth is significant due to the increase in the thickness of the thermal and concentration boundary layers. It is expected that, an increase in the permeability of porous medium lead to a rise in the flow of the fluid through it, since when the holes of the porous medium become large, the resistance of the medium may be neglected. Figure 11 depicts the effects of coupling constant or material parameter on the velocity components. The stream velocity is slightly affected by the coupling constant. As we move away from the stretching sheet surface, η > 1, the stream velocity decreases as N₁ increases. We observe also in Figure 11 that the velocity across the plate monotonically decreases as N₁ increases. We observe in Figure 11 that for values of η less than two, the angular velocity increases when N₁ increases, and thereafter we have a cross-flow angular velocity when increasing values of N₁ cause the angular velocity to decrease.

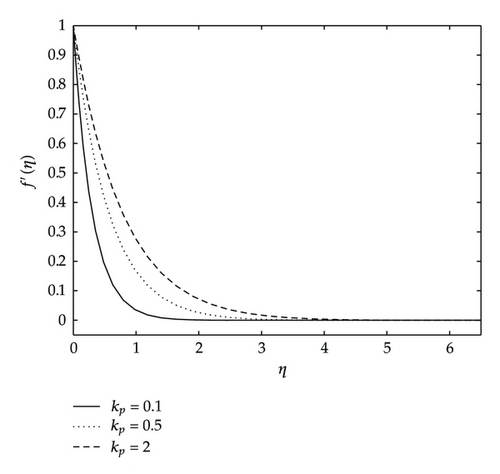
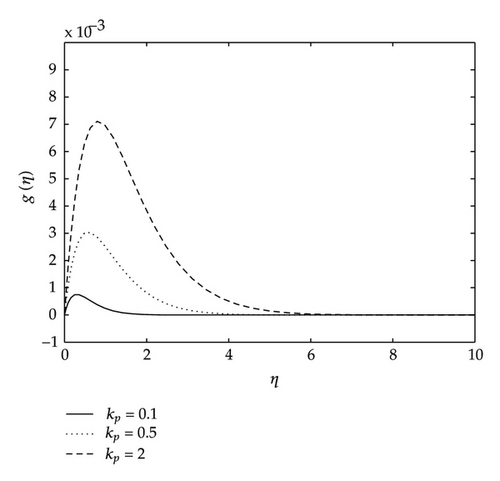
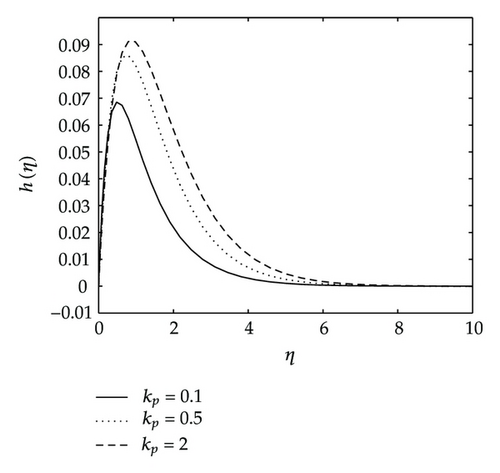
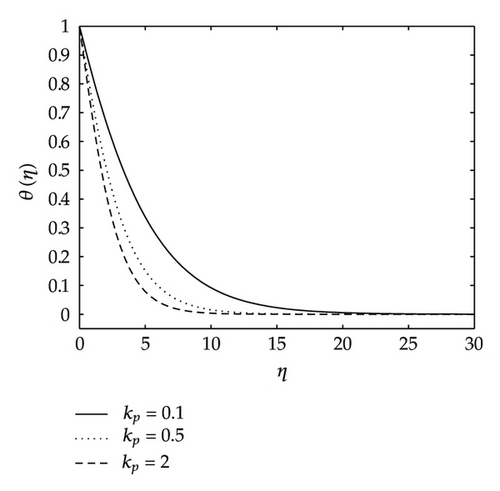
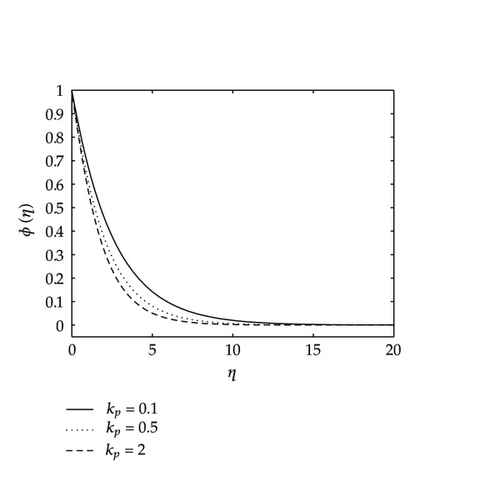
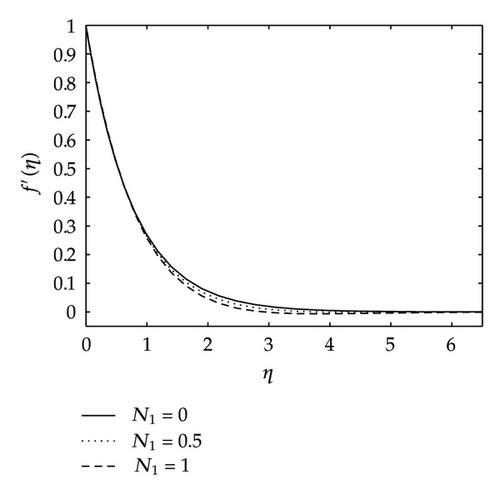
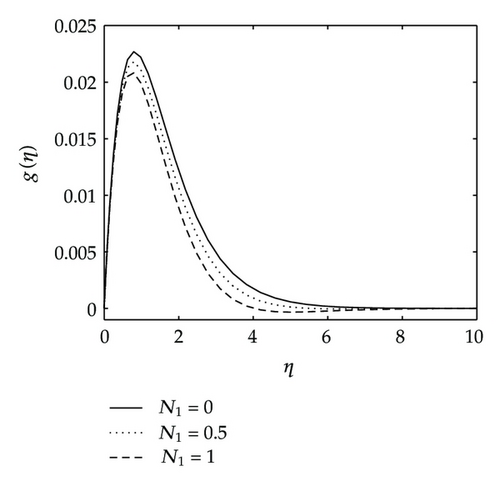
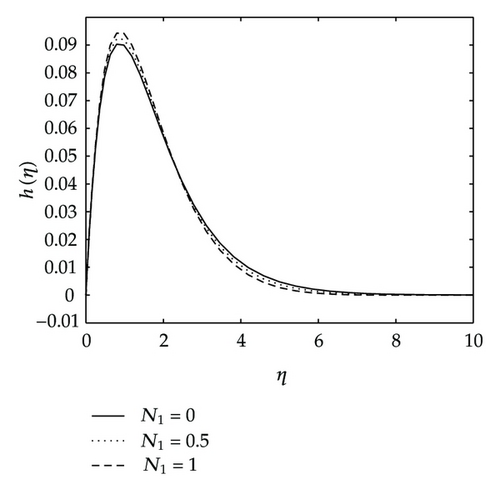
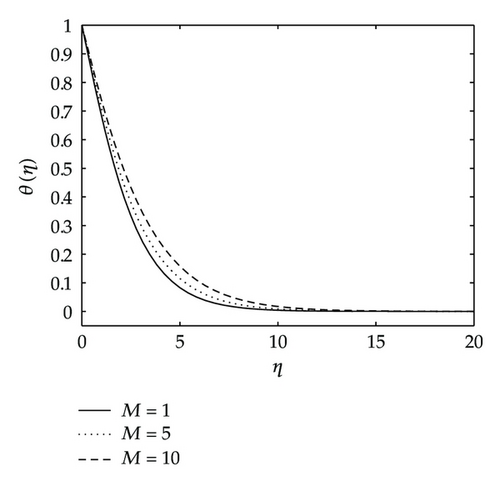
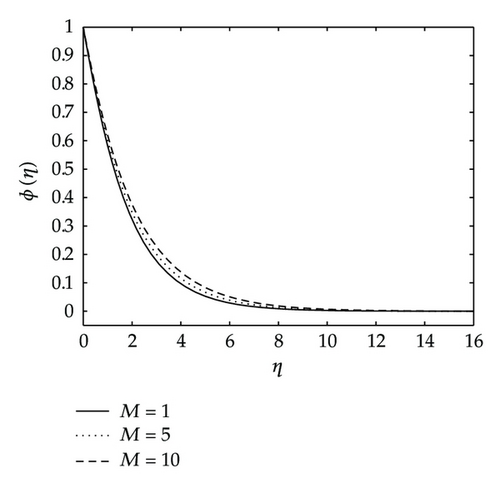
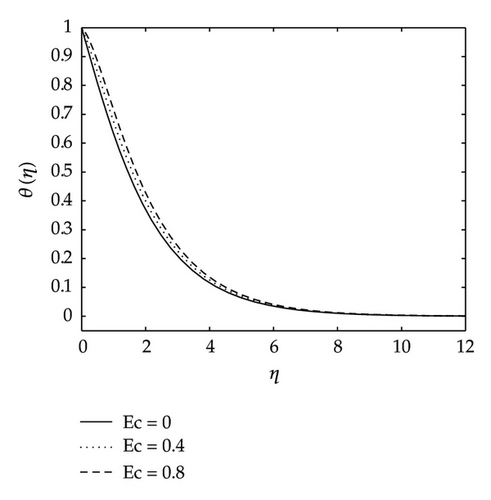
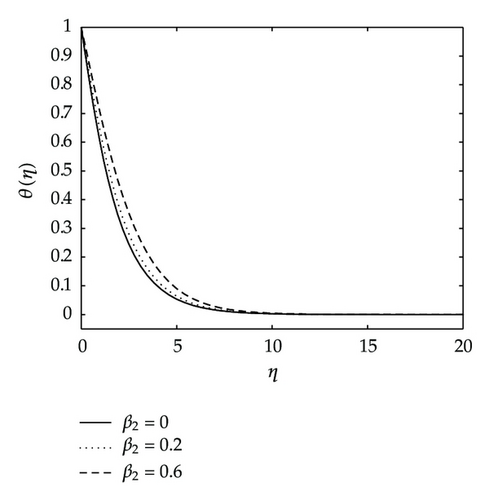
Figure 12 shows the effects of the Eckert number Ec and the variable thermal diffusivity parameter β₂ on the temperature. The temperature distribution θ(η) increases as Ec and β₂ increase as shown in Figure 12.

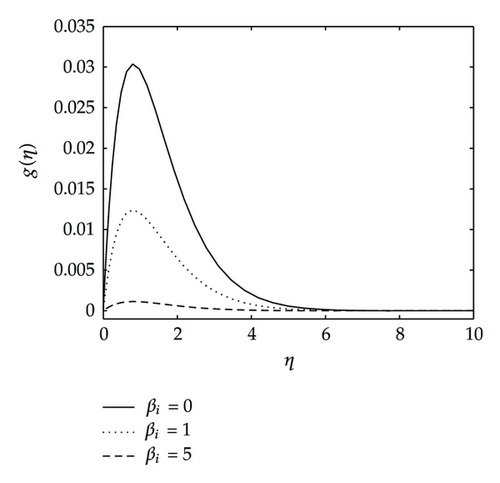
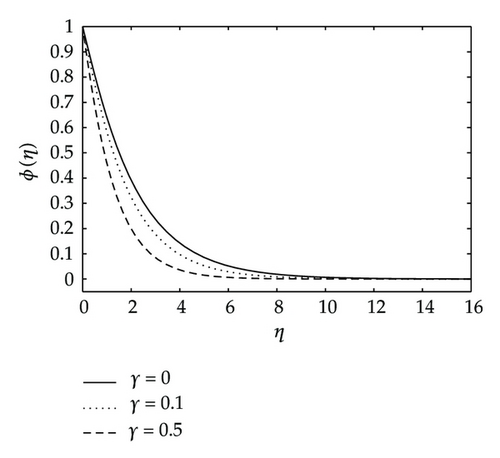
Finally, Figure 13 shows the effects of the ion-slip parameter β_i on the velocity across the plate g(η) and those of the chemical reaction on the concentration distribution ϕ(η). We observe in this figure that the ion-slip parameter has a significant effect on the induced velocity in the z-direction. The velocity component decreases with increases in the parameter β_i. We also observe in this study (not shown for brevity) that f^′(η), h(η), and θ(η) profiles increase as the ion-slip parameter increases. From Figure 13 we also observe that the effects of chemical reaction parameter is to reduce the concentration distribution ϕ(η) when γ increases.

6. Conclusions

In this study, the effects of Hall and ion-slip currents, chemical reaction and variable thermal diffusivity on magnetomicropolar fluid flow through a porous medium past a stretching sheet in the presence of heat and mass transfer have been numerically analyzed using the successive linearization method together with Chebyshevcollocation method. Results for the wall stresses, local Nusselt and Sherwood numbers as well as the details of the velocities, temperature and concentration distributions are presented in tabular and/or graphical forms for the governing parameters. The successive linearization method was found to be a very efficient and accurate method which we hope to apply to different problems in fluid mechanics and related fields. The study observed that higher values of the coupling parameter results in lower stream velocity and velocity across the plate but have little effects on the angular velocity. The porous medium impact on the boundary layer growth is significant due to the increase in the thickness of the hydrodynamic boundary layer and the decrease in the thickness of the thermal and concentration boundary layers. All the velocity components increase with increasing values of the Hall current. The ion-slip current causes the induced velocity in the z-direction to decrease but has opposing effects on the stream velocity, angular velocity, as well as temperature profiles.

Acknowledgment

The authors wish to acknowledge financial support from the University of Swaziland, University of Venda, and the National Research Foundation (NRF).

References

1 Eringen A. C., Theory of micropolar fluids, Journal of Mathematics and Mechanic. (1966) 16, 1–18, 0204005.
Web of Science® Google Scholar
2 Chamkha A. J., MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with hall effects, Applied Mathematical Modelling. (1997) 21, no. 10, 603–609, 2-s2.0-0031252068, https://doi.org/10.1016/S0307%2D904X(97)00084%2DX, ZBL0901.76077.
10.1016/S0307-904X(97)00084-X
Web of Science® Google Scholar
3 Seddeek M. A., Effects of hall and ion-slip currents on magneto-micropolar fluid and heat transfer over a non-isothermal stretching sheet with suction and blowing, Proceedings of the Royal Society A. (2001) 457, no. 2016, 3039–3050, 2-s2.0-57249085640, https://doi.org/10.1098/rspa.2001.0847, ZBL0996.76097.
10.1098/rspa.2001.0847
Web of Science® Google Scholar
4 Takhar H. S., Chamkha A. J., and Nath G., MHD flow over a moving plate in a rotating fluid with magnetic field, hall currents and free stream velocity, International Journal of Engineering Science. (2002) 40, no. 13, 1511–1527, 2-s2.0-0036680143, https://doi.org/10.1016/S0020%2D7225(02)00016%2D2, ZBL1211.76157.
10.1016/S0020-7225(02)00016-2
Web of Science® Google Scholar
5 Shateyi S., Sibanda P., and Motsa S. S., Magnetohydrodynamic flow past a vertical plate with radiative heat transfer, Journal of Heat Transfer. (2007) 129, no. 12, 1708–1713, 2-s2.0-38849158543, https://doi.org/10.1115/1.2767750.
10.1115/1.2767750
Web of Science® Google Scholar
6 Shateyi S., [email protected], Motsa S. S., and [email protected], Sibanda P., [email protected], The effects of thermal radiation, hall currents, soret, and dufour on MHD flow by mixed convection over a vertical surface in porous media, Mathematical Problems in Engineering. (2010) 2010, 20, 627475, https://doi.org/10.1155/2010/627475.
10.1155/2010/627475
Web of Science® Google Scholar
7 Salem A. M. and Abd El-Aziz M., Effect of hall currents and chemical reaction on hydromagnetic flow of a stretching vertical surface with internal heat generation/absorption, Applied Mathematical Modelling. (2008) 32, no. 7, 1236–1254, 2-s2.0-40649084089, https://doi.org/10.1016/j.apm.2007.03.008.
10.1016/j.apm.2007.03.008
Web of Science® Google Scholar
8 Takhar H. S., Chamkha A. J., and Nath G., Flow and mass transfer on a stretching sheet with a magnetic field and chemically reactive species, International Journal of Engineering Science. (2000) 38, no. 12, 1303–1314, 2-s2.0-0033746641, https://doi.org/10.1016/S0020%2D7225(99)00079%2D8, ZBL1210.76205.
10.1016/S0020-7225(99)00079-8
CAS Web of Science® Google Scholar
9 Muthucumaraswamy R. and Ganesan P., Diffusion and first-order chemical reaction on impulsively started infinite vertical plate with variable temperature, International Journal of Thermal Sciences. (2002) 41, no. 5, 475–479, 2-s2.0-0036238391, https://doi.org/10.1016/S1290%2D0729(02)01340%2D6.
10.1016/S1290-0729(02)01340-6
CAS Web of Science® Google Scholar
10 Shateyi S., Thermal radiation and buoyancy effects on heat and mass transfer over a semi-infinite stretching surface with suction and blowing, Journal of Applied Mathematics. (2008) 2008, 12, 414830, 2466249, https://doi.org/10.1155/2008/414830, ZBL1158.80312.
10.1155/2008/414830
Google Scholar
11 Shateyi S. and [email protected], Motsa S. S., [email protected], Thermal radiation effects on heat and mass transfer over an unsteady stretching surface, Mathematical Problems in Engineering. (2009) 2009, 13, 965603, https://doi.org/10.1155/2009/965603, ZBL1191.80029.
10.1155/2009/965603
Web of Science® Google Scholar
12 Elgazery N. S., [email protected], The effects of chemical reaction, hall and ion-slip currents on MHD flow with temperature dependent viscosity and thermal diffusivity, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1267–1283, https://doi.org/10.1016/j.cnsns.2007.12.009.
10.1016/j.cnsns.2007.12.009
Web of Science® Google Scholar
13 Srinivasacharya D. and RamReddy C., Heat and mass transfer by natural convection in a doubly stratified non-Darcy micropolar fluid, International Communications in Heat and Mass Transfer. (2010) 37, no. 7, 873–880, 2-s2.0-77955279681, https://doi.org/10.1016/j.icheatmasstransfer.2010.05.001.
10.1016/j.icheatmasstransfer.2010.05.001
CAS Web of Science® Google Scholar
14 Ishak A., Nazar R., and Pop I., Heat transfer over an unsteady stretching permeable surface with prescribed wall temperature, Nonlinear Analysis: Real World Applications. (2009) 10, no. 5, 2909–2913, 2-s2.0-64449088714, https://doi.org/10.1016/j.nonrwa.2008.09.010, ZBL1162.76017.
10.1016/j.nonrwa.2008.09.010
Web of Science® Google Scholar
15 Elshehawey E. F., Eldabe N. T., Elbarbary E. M. E., and [email protected], Elgazery N. S., Chebyshev finite-difference method for the effects of hall and ion-slip currents on magnetohydrodynamic flow with variable thermal conductivity, Canadian Journal of Physics. (2004) 82, no. 9, 701–715, https://doi.org/10.1139/P04%2D038.
10.1139/p04-038
CAS Web of Science® Google Scholar
16 Seddeek M. A. and Salama F. A., The effects of temperature dependent viscosity and thermal conductivity on unsteady MHD convective heat transfer past a semi-infinite vertical porous moving plate with variable suction, Computational Materials Science. (2007) 40, no. 2, 186–192, 2-s2.0-34447343089, https://doi.org/10.1016/j.commatsci.2006.11.012.
10.1016/j.commatsci.2006.11.012
CAS Web of Science® Google Scholar
17 Shateyi S. and Motsa S. S., Variable viscosity on magnetohydrodynamic fluid flow and heat transfer over an unsteady stretching surface with hall effect, Boundary Value Problems. (2010) 2010, 20, 257568, 2719288, https://doi.org/10.1155/2010/257568, ZBL1195.76438.
10.1155/2010/257568
Google Scholar
18 Mahmoud M. and Waheed S., Effects of slip and heat generation/absorption on MHD mixed convection flow of a micropolar fluid over a heated stretching surface, Mathematical Problems in Engineering. (2010) 2010, 20, 579162, 2684761, https://doi.org/10.1155/2010/579162, ZBL1195.76434.
10.1155/2010/579162
Web of Science® Google Scholar
19 Makukula Z. G., Sibanda P., and Motsa S. S., A novel numerical technique for two-dimensional laminar flow between two moving porous walls, Mathematical Problems in Engineering. (2010) 2010, 15, 528956, 2726293, https://doi.org/10.1155/2010/528956, ZBL1195.76387.
10.1155/2010/528956
Web of Science® Google Scholar
20 Makukula Z. G., Sibanda P., and Motsa S. S., A note on the solution of the von Kármán equations using series and Chebyshev spectral methods, Boundary Value Problems. (2010) 2010, 17, 471793, 2728258, https://doi.org/10.1155/2010/471793, ZBL1207.35248.
10.1155/2010/471793
Google Scholar
21 Makukula Z. G., Sibanda P., and Motsa S. S., On new solutions for heat transfer in a visco-elastic fluid between parallel plates, International Journal of Mathematical Models and Methods in Applied Sciences. (2010) 4, no. 4, 221–230, 2-s2.0-78549272062.
Google Scholar
22 Makukula Z., Motsa S., and Sibanda P., On a new solution for the viscoelastic squeezing flow between two parallel plates, Journal of Advanced Research in Applied Mathematics. (2010) 2, no. 4, 31–38, 2792671, https://doi.org/10.5373/jaram.455.060310.
10.5373/jaram.455.060310
Google Scholar
23 Shateyi S. and [email protected], Motsa S. S., [email protected], A new approach for the solution of three-dimensional magnetohydrodynamic rotating flow over a shrinking sheet, Mathematical Problems in Engineering. (2010) 2010, 15, 586340, https://doi.org/10.1155/2010/586340, ZBL1202.76157.
10.1155/2010/586340
Web of Science® Google Scholar
24 Motsa S. S. and Shateyi S., Successive linearisation solution of free convection non-Darcy flow with heat and mass transfer, Advanced Topics in Mass Transfer, 2011, InTech, Croatia, 425–438.
10.5772/14519
Google Scholar
25 Shateyi S. and Motsa S. S., Hydromagnetic non-Darcy flow, heat and mass transfer over a stretching sheet in the presence of thermal radiation and Ohmic dissipation, Canadian Journal of Chemical Engineering. (2011) 89, no. 6, 1388–1400, https://doi.org/10.1002/cjce.20499.
10.1002/cjce.20499
CAS Web of Science® Google Scholar
26 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods in Fluid Dynamics, 1988, Springer, Berlin, Germany, 917480.
10.1007/978-3-642-84108-8
Google Scholar
27 Don W. S. and Solomonoff A., Accuracy and speed in computing the Chebyshev collocation derivative, SIAM Journal on Scientific Computing. (1995) 16, no. 6, 1253–1268, 1355492, https://doi.org/10.1137/0916073, ZBL0840.65010.
10.1137/0916073
Web of Science® Google Scholar
28 Trefethen L. N., Spectral Methods in MATLAB, 2000, 10, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, Pa, USA, Software, Environments, and Tools, 1776072.
10.1137/1.9780898719598
Google Scholar

Citing Literature

All articles

The Effects of Chemical Reaction, Hall, and Ion-Slip Currents on MHD Micropolar Fluid Flow with Thermal Diffusivity Using a Novel Numerical Technique

Abstract

1. Introduction

2. Problem Formulation

3. Generalization of the Successive Linearisation Method (SLM)

4. Numerical Solution

5. Results and Discussion

6. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Effects of Chemical Reaction, Hall, and Ion-Slip Currents on MHD Micropolar Fluid Flow with Thermal Diffusivity Using a Novel Numerical Technique

Abstract

1. Introduction

2. Problem Formulation

3. Generalization of the Successive Linearisation Method (SLM)

4. Numerical Solution

5. Results and Discussion

6. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Related

Information