Journal of Applied Mathematics
Volume 2012, Issue 1 587834
Research Article
Open Access

Viscous Flow over Nonlinearly Stretching Sheet with Effects of Viscous Dissipation

Javad Alinejad, 

Corresponding Author

Javad Alinejad

Department of Mechanical Engineering, Sari Branch, Islamic Azad University, Sari 48161-19318, Iran iau.ac.ir

Search for more papers by this author
Sina Samarbakhsh, 

Sina Samarbakhsh

Azmoon Pardazesh Research Institute, No. 2, Malekloo Street, Narmak, Tehran 1483764874, Iran azmoonpardazesh.com

Search for more papers by this author
First published: 16 May 2012
https://doi.org/10.1155/2012/587834
Citations: 35
Academic Editor: M. F. El-Amin

Abstract

The flow and heat transfer characteristics of incompressible viscous flow over a nonlinearly stretching sheet with the presence of viscous dissipation is investigated numerically. The similarity transformation reduces the time-independent boundary layer equations for momentum and thermal energy into a set of coupled ordinary differential equations. The obtained equations, including nonlinear equation for the velocity field f and differential equation by variable coefficient for the temperature field θ, are solved numerically by using the fourth order of Runge-Kutta integration scheme accompanied by shooting technique with Newton-Raphson iteration method. The effect of various values of Prandtl number, Eckert number and nonlinear stretching parameter are studied. The results presented graphically show some behaviors such as decrease in dimensionless temperature θ due to increase in Pr number, and curve relocations are observed when heat dissipation is considered.

1. Introduction

The study of two-dimensional boundary layer flow, heat, and mass transfer over a nonlinear stretching surface is very important as it finds many practical applications in different areas. Some industrial applications of viscous flow over a stretching sheet are aerodynamic extrusion of plastic sheets, condensation process of metallic plate in a cooling bath, and extrusion of a polymer sheet from a dye. During the manufacture of these sheets, the melt issues from a slit and is subsequently stretched to achieve the desired thickness. The final products of desired characteristics are notably influenced by the stretching rate, the rate of the cooling in the process, and the process of stretching. Viscous dissipation changes the temperature distributions by playing a role like an energy source, which leads to affecting heat transfer rates. The merit of the effect of viscous dissipation depends on whether the sheet is being cooled or heated. The problem of nonlinear stretching sheet for different cases of fluid flow has also been analyzed by different researchers. Sakiadis [1] initiated the study of boundary layer flow over a continuous solid surface moving with constant speed as result of ambient fluid movement; this boundary flow is generally different from boundary layer flow over a semi-infinite flat plate. Erickson [2] studied this problem to the case in which the transverse velocity at the moving surface is nonzero with the effects of heat and mass transfer being taken in to account. Danberg and Fansler [3], using nonsimilar solution method, studied the flow inside the boundary layer past a wall that is stretched with a velocity proportional to the distance along the wall. P. S. Gupta A. S. Gupta [4], using similar solution method, analyzed heat and mass transfer in the boundary layer over a stretching sheet subject to suction or blowing. The laminar boundary layer on an inextensible continues flat surface moving with a constant velocity in a non-Newtonian fluid characterized by a power-law model is studied by Fox et al. [5], using both exact and approximate methods. Rajagopal et al. [6] studied the flow behavior of viscoelastic fluid over stretching sheet and gave an approximate solution to the flow field. Recently Troy et al. [7] presented an exact solution for Rajagopal problem. Vajravelu and Roper [8] studied the flow and heat transfer in a viscoelastic fluid over a continues stretching sheet with power law surface temperature, including the effects of viscous dissipation, internal heat generation or absorption, and work due to deformation in the energy equation. Vajravelu [9] studied the flow and heat transfer characteristics in a viscous fluid over a nonlinearly stretching sheet without heat dissipation effect. Cortell [10, 11] has worked on viscous flow and heat transfer over a nonlinearly stretching sheet. Raptis and Perdikis [12] studied viscous flow over a nonlinear stretching sheet in the presence of a chemical reaction and magnetic field. Abbas and Hayat [13] addressed the radiation effects on MHD flow due to a stretching sheet in porous space. Cortell [14] investigated the influence of similarity solution for flow and heat transfer of a quiescent fluid over a nonlinear stretching surface. Awang and Hashim [15] obtained the series solution for flow over a nonlinearly stretching sheet with chemical reaction and magnetic field. In the present paper an analysis is carried out to study the flow and heat transfer phenomenon in a viscous fluid over a nonlinearly stretching sheet by considering the effects of heat dissipation. In order to arrive nonlinear ordinary deferential equations, stream function is defined differently (compared to the linear stretching case) and these nonlinear deferential equations along with pertinent boundary condition are solved.

2. Flow and Heat Transfer Analysis

Consider the steady laminar flow of a viscous incompressible over a nonlinearly stretching sheet. The governing boundary layer equations of mass conservation, momentum, and energy with viscous dissipation are
()
where u  and v are the velocity components in x  and y axes, respectively, T is the temperature, ν the kinematic viscosity, ρ the density, μ the dynamic viscosity, k the thermal conductivity, and Cp the specific heat at constant pressure. The boundary conditions to the case are
()
()
These conditions suggest transforming into the corresponding nonlinear ordinary differential equations by choosing the similarity transformation as given by Vajravelu [9]:
()
where a prime denotes differentiation with respect to η. The transformed nonlinear, coupled ordinary differential equations and boundary conditions are
()
()
()
()
()
where dimensionless parameters are defined as
()
The shear stress at the surface of the sheet is defined as
()
And the local wall heat flux is defined as
()
Since there is no exact solution for nonlinearly stretching boundary problem, the differential (2.5) and (2.7) are investigated numerically in accordance with the boundary condition (2.6) and (2.7).

3. Numerical Analysis

The nonlinear boundary value problem represented by (2.5) and (2.7) is solved numerically using fourth-order Runge-Kutta shooting technique. Equations (2.5) and (2.7) have been discretized to five first-order equations as follows:
()
where y1 = f,   y2 = f′,   y3 = f′′,   y4 = θ,   y5 = θ′. Boundary conditions (2.6) and (2.9) become
()
Regarding the above boundary conditions three values out of five that required initial values are known, and we begin solution procedure by two initial guesses and the procedure corrects them using Newton-Raphson iteration scheme. Initial guesses to initiate the shooting process are very crucial in this process and it should be noted that convergence is not guaranteed, especially if a poor guess for the missing starting boundary values is made. Another challenge to solve this equations system is the values of y2 and y4 at η → ∞. It is necessary to estimate η by a known value in which dimensionless temperature profile (θ) reaches its asymptotic state.

4. Results and Discussion

Figures 1, 2, 3, 4, 5, and 6 described the behavior of dimensionless temperature profile (θ)  versus similarity variable η which are compared for two cases of without heat dissipation and by considering heat dissipation effects. It can be seen that in cases with positive values of the Eckert number, the curves are shifted to the right-hand side and in cases with negative values of the Eckert number the curves are shifted to the left-hand side. This is due to involvement of heat dissipation. Furthermore, it is obvious that the dimensionless temperature θ  increases with increases in the nonlinear stretching parameter n (Figures 7 and 8).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation with Pr = 7, n = 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation with Pr = 0.71, n = 1.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation with Pr = 7, n = 5.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation with Pr = 0.71, n = 5.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation with Pr = 7, n = 10.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation with Pr = 0.71, n = 10.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation and nonlinear parameter n with Pr = 7.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of heat dissipation and nonlinear parameter n with Pr = 0.71.

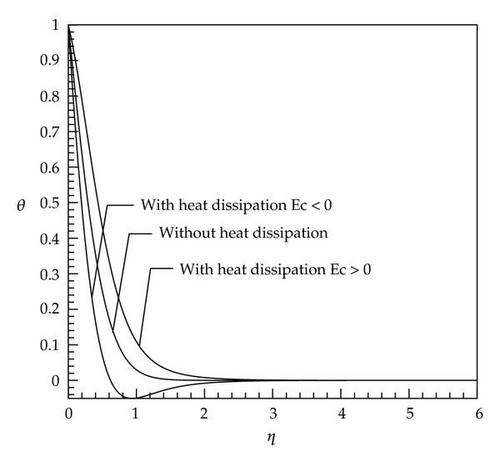
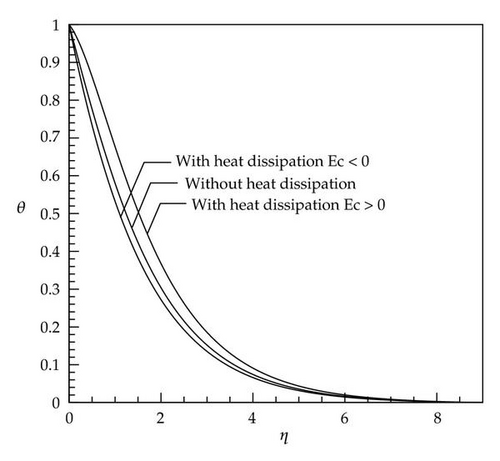
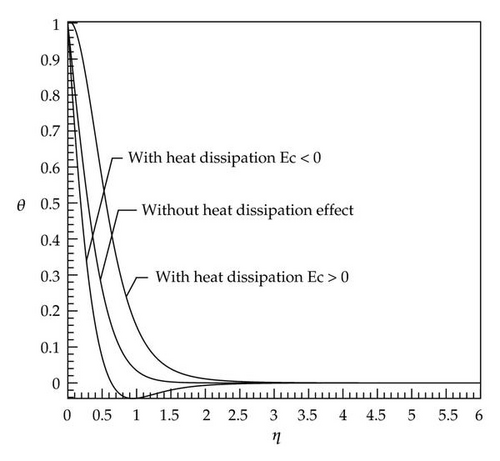
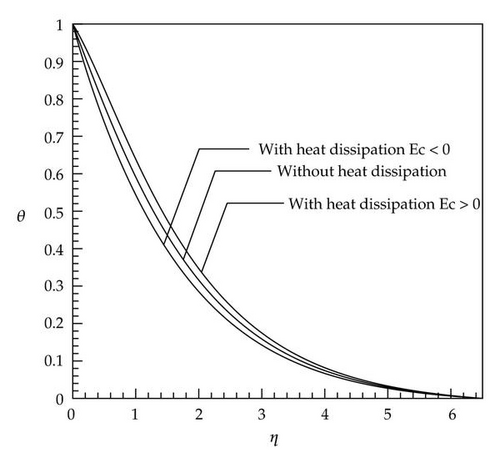
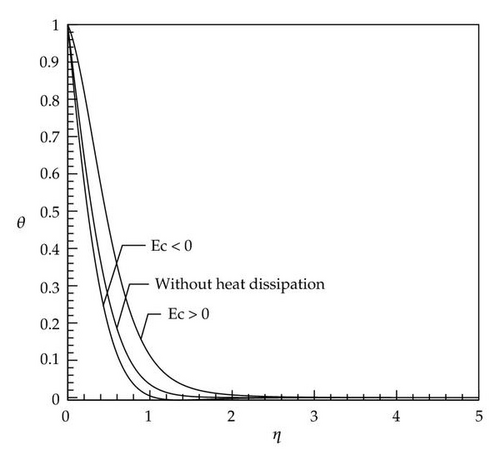
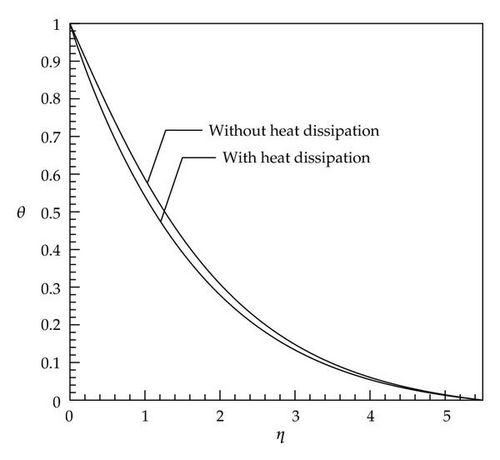
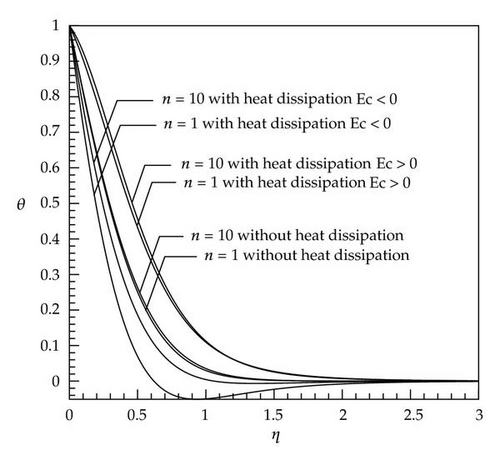
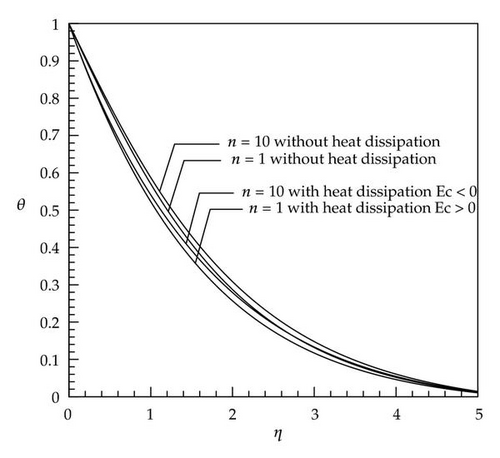
It is seen that the dimensionless temperature θ  at a point in the flow decreases with an increase in the Prandtl number (Figure 9). Since the Prandtl number is a criterion of relative diffusion effects of momentum and energy in velocity and thermal boundary layer, respectively, therefore, this result is consistent with the fact that the thermal boundary layer thickness decreases with an increase in the Prandtl number (see the scales of Figures 1 and 2).

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Dimensionless temperature profile  θ versus similarity parameter  η-Effect of Pr number for n = 5, Ec = −1.

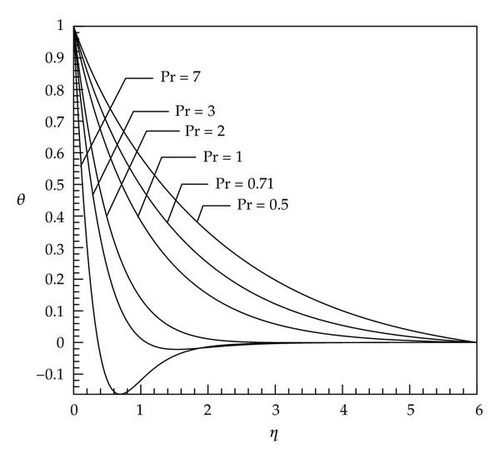
In cases with small Prandtl number (Pr < 1, Figures 2, 4, and 6), there is a very low difference at the end of diagram between the curves with and without heat dissipation (the end of boundary layer thickness) which caused by this fact that, in these cases, the thickness of thermal boundary layer is greater than that of velocity boundary layer and at the end of thermal boundary layer in which velocity gradient is reduced to zero, the curves have conformity on each other because the effect of the energy produced by viscosity is destroyed. In cases with large Prandtl number (Pr > 1) and negative Eckert number, the dimensionless temperature θ  gains a negative value after reaching zero and, at the end of path, it reaches zero again (Figures 1, 3, and 5). The reason for being negative of θ in a specific domain is the presence of velocity gradient outside the thermal boundary layer. These negative values by considering larger Eckert number are more significant. As soon as velocity gradient is removed (at the end of velocity boundary layer) the θ reaches zero again. In Figure 9, for a constant Eckert number the dimensionless temperature θ is drawn based on different Prandtl number. It is observed that, in larger Prandtl number due to the above-mentioned reasons, θ has smaller value. The dimensionless temperature profiles presented in Figures 1–9 show that the far-field boundary conditions are satisfied asymptotically, which support the validity of the numerical results presented.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.