Many problems of mechanics and physics are posed in unbounded (or infinite) domains. For solving these problems one typically limits them to bounded domains and find ways to set appropriate conditions on artificial boundaries or use quasi-uniform grid that maps unbounded domains to bounded ones. Differently from the above methods we approach to problems in unbounded domains by infinite system of equations. In this paper we present starting results in this approach for some one-dimensional problems. The problems are reduced to infinite system of linear equations. A method for obtaining approximate solution with a given accuracy is proposed. Numerical experiments for several examples show the effectiveness of the offered method.

1. Introduction

Many problems of mechanics and physics are posed in unbounded (or infinite) domains, for example, heat transport problems in infinite or semi-infinite bar, aerosol propagation in atmosphere, problem of ocean pollution, wave propagation in unbounded media, and problem of computing the potential distribution due to a source of current in or on the surface of the Earth. For solving these problems one usually restricts oneself to treat the problem in a bounded domain and try to use available efficient methods for finding exact or approximate solutions in the restricted domain. But there arise some questions: which size of restricted domain is enough and how to set conditions on artificial boundary for obtaining approximate solution with good accuracy? The simplest way to do this is to transfer boundary condition on infinity to the artificial boundary. This raw way may lead to large deviation of approximate solution from the solution of the original problem. Therefore, instead of transferring boundary condition on infinity without changes one tries to set appropriate conditions on artificial boundary. This is a direction of researches that attracts the attention of many specialists in the fields of mathematics, mechanics, and physics (see [1–4]). Especially, from the late 1970s for the wave problems the nonreflecting boundary conditions are intensively developed (see [5–7] and bibliography therein).

Recently, a few of Russian mathematicians proposed a new method for problems in unbounded domains. It is the use of quasi-uniform grid for mapping unbounded domain to bounded one [8–12]. This quasi-uniform grid was used after in [13]. Due to this grid the condition on infinity is easily taken into account. Nevertheless, the quasi-uniform grid, as will be shown later by us, cannot satisfy the requirements to describe the wave propagation when the area under interest, which is peak of waves, is covered by very sparse grid points.

Differently from the above methods we approach to problems in unbounded domain by infinite system of linear equations. More precisely, we construct a different scheme for the problem in unbounded domain and suggest a method for treating the infinite system in order to obtain an approximate solution with a given accuracy. This method is based on a theorem about error estimate of the solution of a truncated system obtained from an infinite tridiagonal system. It should be noticed that the reduction of infinite systems of grid equations to finite systems are also considered recently in [14, 15].

In this paper we report some our starting results in the research direction for several one-dimensional stationary and nonstationary problems in unbounded domains. Some numerical examples demonstrate the efficiency of the proposed method and its advantage over the quasi-uniform grid method.

2. Some Concepts and Auxiliary Results

2.1. Infinite System of Equations [16]

Infinite system of linear equations with infinite number of unknowns is the system of the form

()

A sequence of numbers x₁, x₂, … is called a solution of the system (2.1) if after the substitution of these numbers into the right hand sides we obtain convergent series and all equalities are satisfied.

Suppose that the system has solutions. Then the solution found by the method of successive approximation (or simple iteration)

()

with the zero starting approximation

is called the main solution of the system.

We say that a solution x₁, x₂, … of the system tends to zero if x_i → 0 as i → ∞.

We are interested in the system for which

. Set

()

The system (2.1) is called regular system if

()

it is called completely regular if there exists a constant θ > 0 such that

()

Assume that there exists a number K such that the free members b_i satisfy the condition

()

Theorem 2.1 (see [16], Theorem Ia.)The regular system (2.1) with the free members satisfying the condition (2.6) has a bounded solution |x_i | ≤ K which can be found by the method of successive approximation.

Theorem 2.2 (see [16], Theorem IIb.)A regular infinite system cannot have more than one solution tending to zero. Moreover, if its coefficients and free members are positive then its positive solution tending to zero must be the main solution.

Theorem 2.3 (see [16], Theorem IVa.)The main solution of the regular system (2.1) with the free members satisfying the condition (2.6) can be found by the truncation method, that is, if is the solution of the finite system

()

then

()

where

(i = 1, 2, …) is the main solution of the system.

2.2. Quasi-Uniform Grid [8, 10]

Let x(ξ) be strictly monotone smooth function of the argument ξ ∈ [0,1]. The grid

()

with x(0) = a, x(1) = +∞ is called quasi-uniform grid on [a, +∞]. In this case the last node x_N of the grid is on the infinity.

Example of quasi-uniform grids are the grids

()

3. Method of Infinite System for Stationary Problems

We will present in details the method of infinite system on the model problem of heat conductivity in a semi-infinite bar

()

under the usual assumptions that the functions k(x), d(x), and f(x) are continuous and

()

In the case if k, d are constants and f(x) has a compact support [0, L] one can easily find the exact artificial boundary condition at x = L with the help of Dirichlet-to-Neumann map [4]. If f(x) has no compact support but has special form such that it is possible to find a particular solution of the equation

()

then an exact artificial boundary condition can be established. In general case when k, d, and f only satisfy the condition (3.2) one cannot find the exact condition at x = L if the problem is restricted to finite interval [0, L]. Below we consider this case.

In order to solve the problem (3.1)-(3.2) we introduce the uniform grid {x_i = ih, i = 0,1, …} and consider the difference scheme

()

where

()

Now we rewrite the difference scheme in the form of customary three-point difference equations

()

Here

()

Putting

()

we can rewrite the system (3.6) in the canonical form of infinite system as follows:

()

We have ρ₀ = 1 − p₀ − q₀ = 1 and from (3.7), (3.8) it follows

()

Thus, the system (3.9) is regular. More precisely, it is completely regular because it is easy to verify that

()

where

()

Now consider r_i/ρ_i. From (3.8) and (3.10) we have r_i/ρ_i = f_i/d_i, and from the assumptions (3.2) it follows that f_i/d_i → 0. Therefore, there exists a constant K^* such that |f_i | ≤ K^*d_i for any i. Consequently, the conditions of Theorem 2.3 are satisfied and the solution of the infinite system (3.8) can be found by the truncation method.

A question that arises here is to which size do we need to truncate the infinite system for obtaining approximate solution with a given accuracy? Below we give answer to this question.

Following the progonka method (or Thomas algorithm) which is a special form of the Gauss elimination [17] for tridiagonal system of equations we shall seek the solution of (3.9) in the form

()

where coefficients are calculated by the formulas:

()

Lemma 3.1. For the coefficients α_i and β_i there hold the following assertions.

(i)
0 < α_i < 1, (i = 2,3, …) and β_i → 0 as i → ∞.
(ii)
|β_i|/(1 − α_i) → 0 as i → ∞.

Proof. (i) Analogously as for a finite system of three-point difference equations (see [17]) it is possible to prove by induction that 0 < α_i < 1 (i = 2, 3, …). Hence, from the condition y_i → 0 and from (3.13) it follows that β_i → 0 as i → ∞.

(ii) Since 0 < α_i < 1 is proved, from (3.10) and (3.11) we have

()

Further, taking into account (3.8) and (3.9) we obtain

()

Put

()

Then there holds the estimate

()

Therefore,

()

The proof of the lemma is complete.

Theorem 3.2. Given an accuracy ε > 0. If starting from a natural number N there holds

()

then for the deviation of the solution of the truncated system

()

compared with the solution of the infinite system (3.9) there holds the following estimate

()

Proof. Denote . Then it is easy to see that z_i satisfies the infinite system

()

where

()

This system is regular because for it ρ_i = 1 − α_i+1 > 0 due to 0 ≤ α_i < 1 (i = 1, 2, …) as was said above. Besides, the condition (3.20) yields |b_i| ≤ ερ_i. Therefore, by the theory of infinite systems we have the estimate |z_i | ≤ ε (i = 0, 1, …). The theorem is proved.

Remark 3.3. The above theorem permits us in the process of computation of the sweep coefficients (3.14) to determine when to truncate the infinite system (3.9) for guarantee that the solution of the infinite system less than given ε.

Below in order to illustrate the effectiveness of using Theorem 3.2 we consider the following.

Example 3.4.

()

where

()

This problem has the exact solution u(x) = 1/(1 + x²). Construct the infinite system (3.9) and truncate it when Theorem 3.2 is satisfied. The solution of the truncated system is compared with the exact solution. The results of computation on the uniform grid with step h = 0.1 and h = 0.05 are given in the Tables 1 and 2, where N is the size of the system, that is, automatically truncated,

()

The graphs of the exact and approximate solutions are given in Figure 1, meanwhile the graph of the right-hand side is given in Figure 2.

Table 1. Case h = 0.1.

ε	N	Error
0.01	108	0.0085
0.001	325	0.0012
0.0001	1010	0.0012

Table 2. Case h = 0.05.

ε	N	Error
0.01	215	0.0086
0.001	650	9.45e − 4
0.0001	2020	2.94e − 4

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Exact versus approx. solution.

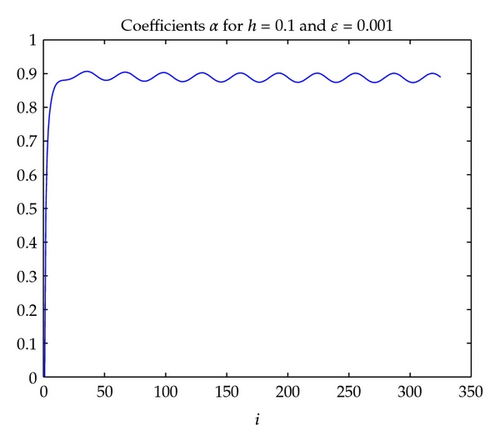
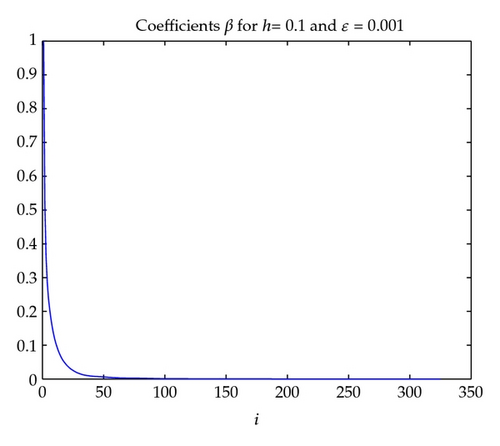
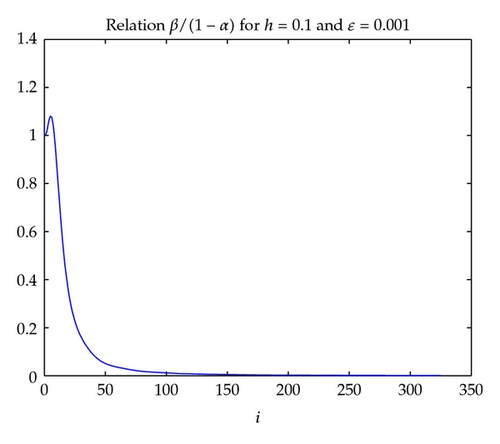
In the process of computation we observe that the coefficients β_i tend to zero very fast and the coefficients α_i have the trend of approaching to 1 but the ratio β_i/(1 − α_i) tend to zero rather fast, too. The graphs of the coefficients α_i, β_i, and the ratio β_i/(1 − α_i) are given in Figures 3, 4, and 5, respectively.

Remark 3.5. The problem in semi-infinite bar for the more general than (3.1) equation , is treated in similar way if for it we construct according to Samarskii [17] a monotone difference scheme.

Remark 3.6. In the case if instead of Dirichlet boundary condition at left end-point there is given Neumann boundary condition then the problem can be treated in similar way.

Remark 3.7. If the functions k(x), d(x), and f(x) in (3.1) are even functions then the problem on the whole real axis with vanishing conditions, that is, u(±∞) = 0, is reduced to the problem on [0, +∞) with the boundary condition u′(0) = 0.

4. Parabolic Equation on Semi-Infinite Bar

In this section we apply the infinite system technique proposed in the previous section to an initial-boundary problem for parabolic equation.

(a)
First we consider the heat conductivity problem with constant coefficient k > 0
()

This problem has the exact solution

()

Using purely implicit difference scheme on uniform grid with spatial stepsize h and time stepsize τ we reduce the problem (4.1) to infinite system on each time layer j + 1:

()

where r = kτ/h², i, j are indexes of grid nodes in space and in time.

The system (4.3) is treated in a similar way as for the system (3.6). It is easy to show that at each time layer j + 1 for the sweep coefficients α_i and β_i we have 0 < α_i < r/(1 + r) and β_i → 0. So, we can use Theorem 3.2 to truncate the infinite system.

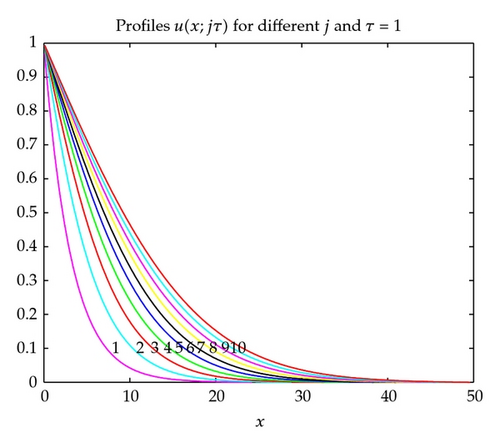
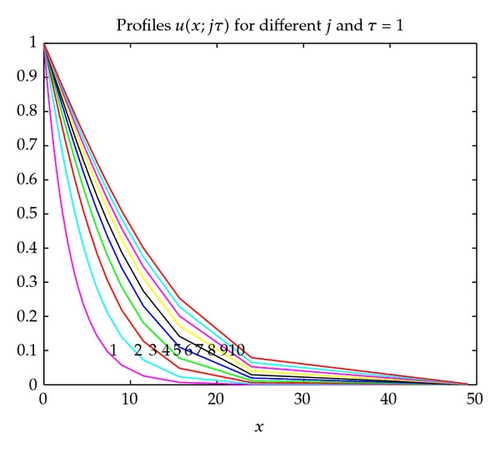
In order to demonstrate the advantage of the infinite system method over the quasi-uniform grid method used in [10, 12] we perform computations by these two methods: infinite system on uniform grid and finite system on quasi-uniform grid x_i = i/N − i, (i = 0,1, …, N) with N = 50. Since the density of quasi-uniform nodes is very sparse for i ≥ 25 the profiles of the approximate solution are broken lines. Figures 6 and 7 give the profiles of solution computed by the two methods with k = 10, ε = 0.001. From these figures we see that the infinite system method gives better results.

(b)
The stationary problem of air pollution caused by a point source with constant power Q located at point (0, H) is reduced to the problem
()

where φ is the concentration of aerosol, u is the wind velocity in the x-direction, w_g is the falling velocity of pollutants by gravity, σ ≥ 0 is the coefficient of transformation, ν-the vertical diffusion coefficient, and α ≥ 0-the coefficient characterizing the reflection and absorption of the bedding surface [18, 19].

The numerical solution of the above problem on uniform grid using the infinite system method was studied in [18], where a theorem similar to Theorem 3.2 was proved.

An interesting fact was established in [20]. It is that if limiting the problem of air pollution to the domain 0 ≤ z ≤ Z with finite Z then artificial boundary condition φ(x, Z) = 0 causes an undershoot and the Neumann condition ∂φ/∂z(x, Z) = 0 causes an overshoot in numerical solution when compared with the solution of the problem with the boundary condition φ(x, +∞) = 0.

5. The Equation of Complex Type

The advantage of the infinite system method in comparison with the quasi-uniform grid method is revealed more clearly in the problems simulating wave phenomena, when high density of grid nodes is near left endpoint and nodes are gradually sparse in the right cannot well describe waves running to the right. To show this fact we consider a problem describing ion wave in stratified incompressible fluid

()

For solving this problem, as in [9], we set ϕ = ∂²u/∂x² − u. Then the problem is decomposed into two consecutive problems of second order

()

On the uniform grid with step sizes h, τ replace the above differential problem by the difference schemes

()

From the explicit scheme (5.3) it is easy to calculate ϕ^j+1. After that we use the infinite system technique for the scheme (5.4) for computing u^j+1. This algorithm is applied to some examples in comparison with the quasi-uniform grid method.

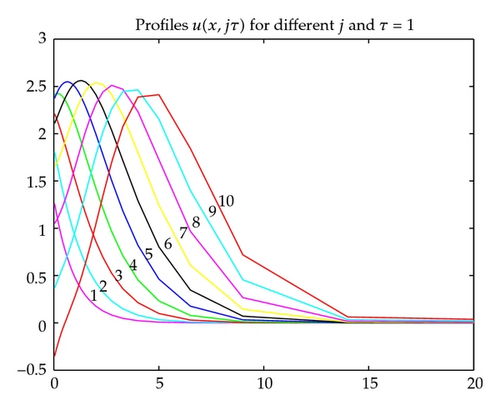
Example 5.1. In this example we take initial conditions be homogeneous and the left boundary condition u(0, t) = arctan²(10t) · sin(0.3t).

The profiles u(x, t) with t = 1,2, …, 10 computed by the infinite system method for h = 0.1 are given in Figure 8 and by the quasi-uniform grid method are given in Figure 9.

Example 5.2. The left boundary condition is zero, the initial condition is

()

The propagation of the initial profile after the time t = 4,6, 8,10, and 12 computed by the infinite system method and by the quasi-uniform grid method are given in Figures 10 and 11, respectively.

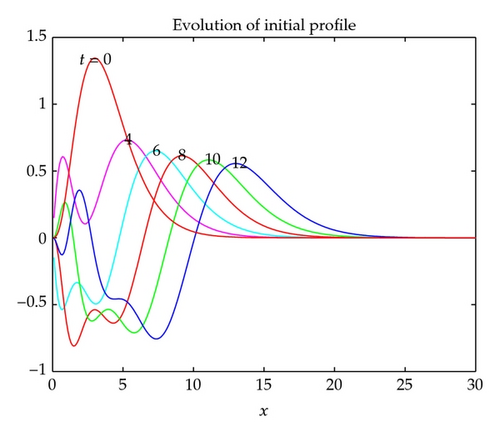
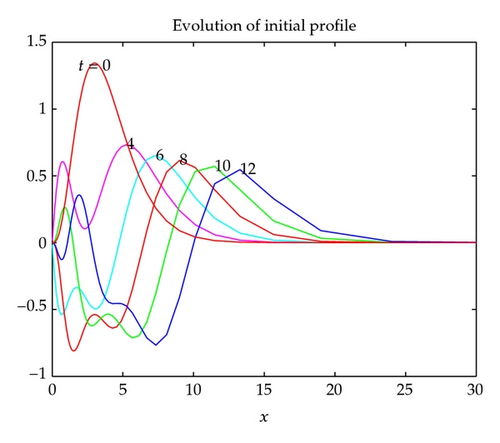
From Figures 8–11 we see that the approximate solution computed by the method of infinite system describes the wave propagation better than the solution obtained by the method of quasi-uniform grid.

6. Concluding Remarks

In this paper we propose and investigate the infinite system method for solving several one-dimensional stationary and nonstationary problems, where the keystone is to determine when truncate the infinite system for assuring to obtain approximate solution with a given accuracy. This method reveals advantage over the quasi-uniform grid method, proposed in 2001 by Russian mathematicians in time-dependent problems, especially in problems of wave propagation.

In combination with the alternating directions method the proposed method can be applied to two-dimensional problems in semi-infinite and infinite strips.

The development of the method for solving other two-dimensional and three-dimensional problems is the direction of our research in the future.

Acknowledgments

This work is supported by Vietnam National foundation for Science and Technology Development (NAFOSTED) under the Grant no. 102.99-2011.24. The authors would like to thank the anonymous reviewers sincerely for their helpful comments to improve the original paper.

References

1 Colonius T., Modeling artificial boundary conditions for compressible flow, Annual Review of Fluid Mechanics. (2004) 36, 315–345.
10.1146/annurev.fluid.36.050802.121930
Web of Science® Google Scholar
2 Quang A D. and Ehrhardt M., Adequate numerical solution of air pollution problems by positive difference schemes on unbounded domains, Mathematical and Computer Modelling. (2006) 44, no. 9-10, 834–856, https://doi.org/10.1016/j.mcm.2006.02.016, 2253755, ZBL1137.65395.
10.1016/j.mcm.2006.02.016
Google Scholar
3 Arnold A., Ehrhardt M., and Sofronov I., Discrete transparent boundary conditions for the Schrödinger equation: fast calculation, approximation, and stability, Communications in Mathematical Sciences. (2003) 1, no. 3, 501–556, 2069942, ZBL1085.65513.
10.4310/CMS.2003.v1.n3.a7
Google Scholar
4 Tsynkov S. V., Numerical solution of problems on unbounded domains. A review, Applied Numerical Mathematics. (1998) 27, no. 4, 465–532, https://doi.org/10.1016/S0168%2D9274(98)00025%2D7, 1644674, ZBL0939.76077.
10.1016/S0168-9274(98)00025-7
Web of Science® Google Scholar
5 Givoli D., High-order local non-reflecting boundary conditions: a review, Wave Motion. (2004) 39, no. 4, 319–326, https://doi.org/10.1016/j.wavemoti.2003.12.004, 2058659, ZBL1163.74356.
10.1016/j.wavemoti.2003.12.004
Web of Science® Google Scholar
6 Givoli D., Nonreflecting boundary conditions, Journal of Computational Physics. (1991) 94, no. 1, 1–29, https://doi.org/10.1016/0021%2D9991(91)90135%2D8, 1103713.
10.1016/0021-9991(91)90135-8
Web of Science® Google Scholar
7 Hagstrom T., Mar-Or A., and Givoli D., High-order local absorbing conditions for the wave equation: extensions and improvements, Journal of Computational Physics. (2008) 227, no. 6, 3322–3357, https://doi.org/10.1016/j.jcp.2007.11.040, 2392736, ZBL1136.65081.
10.1016/j.jcp.2007.11.040
Web of Science® Google Scholar
8 Alshin A. B., Application of quasi-uniform grids for numerical solution of initial boundary value problems in unbounded domains, Proceedings of the International Conference on Differential Equations, July 2003, Hasselt, Belgium, World Scientific, 1024–1026.
Google Scholar
9 Alshin A. B. and Alshina E. A., Numerical solution of initial-boundary value problems for equations of composite type in unbounded domains, Zhurnal Vychislitel′noi Matematiki i Matematicheskoi Fiziki. (2002) 42, no. 12, 1796–1803, 1971891.
Google Scholar
10 Alshin A. B., Alshina E. A., Boltnev A. A., Kacher O. A., and Koryakin P. V., Numerical solution of initial-boundary value problems for Sobolev-type equations on quasi-uniform grids, Zhurnal Vychislitel′noi Matematiki i Matematicheskoi Fiziki. (2004) 44, no. 3, 490–510.
Google Scholar
11 Alshina E. A., Kalitkin N. N., and Panchenko S. L., Numerical solution of boundary value problems in an unbounded domain, Matematicheskoe Modelirovanie. (2002) 14, no. 11, 10–22, 1989789.
Google Scholar
12 Kalitkin N. N., Kuznetsov N. O., and Panchenko S. L., The method of quasiuniform grids in an infinite domain, Doklady Akademii Nauk. (2000) 374, no. 5, 598–601, 1798949, ZBL1045.65021.
CAS Google Scholar
13 Koleva M. N., I. Lirkov, S. Margenov, and J. Wasniewski, Numerical solution of the heat equation in unbounded domains using quasi-uniform grids, Large-Scale Scientific Computing, 2006, 3743, Springer, Berlin, Germany, 509–517, Lecture Notes in Comput. Sciences, https://doi.org/10.1007/11666806_58, 2248635, ZBL1142.65397.
10.1007/11666806_58
Google Scholar
14 Zadorin A. I. and Chekanov A. V., Reduction of three-point difference schemes on an infinite interval to a scheme with a finite number of nodes, Siberian Journal of Computer Mathematics. (2002) 5, 149–161.
Google Scholar
15 Zadorin A. I. and Chekanov A. V., Numerical method for three-point vector difference schemes on infinite interval, International Journal of Numerical Analysis and Modeling. (2008) 5, no. 2, 190–205, 2478699, ZBL1138.65096.
Web of Science® Google Scholar
16 Kantorovich L. V. and Krylov V. I., Approximate methods of Higher Analysis, 1958, Interscience Publishers, New York, NY, USA, 0106537.
Google Scholar
17 Samarskii A. A., The Theory of Difference Schemes., 2001, Marcel Dekker, New York, NY, USA, https://doi.org/10.1201/9780203908518, 1818323.
10.1201/9780203908518
Google Scholar
18 Quang A D. and Van Luoc N., Numerical solution of a stationary problem of air pollution, Proceedings of National Center for Scientific Researches of Vietnam. (1994) 6, no. 1, 11–23.
Google Scholar
19 Van Luoc N., Quang A D., and Dieu N. C., Analytic and numerical solution of some problems of air pollution, Southeast Asian Bulletin of Mathematics. (1993) 105–117.
Google Scholar
20 Quang A D. and Anh N. D., On numerical modelling for dispersion of active pollutants from a elevated point source, Vietnam Journal of Mathematics. (1996) 24, no. 3, 315–325, 2010824.
Google Scholar

Citing Literature

All articles

Method of Infinite System of Equations for Problems in Unbounded Domains

Abstract

1. Introduction

2. Some Concepts and Auxiliary Results

2.1. Infinite System of Equations [16]

2.2. Quasi-Uniform Grid [8, 10]

3. Method of Infinite System for Stationary Problems

4. Parabolic Equation on Semi-Infinite Bar

5. The Equation of Complex Type

6. Concluding Remarks

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Method of Infinite System of Equations for Problems in Unbounded Domains

Abstract

1. Introduction

2. Some Concepts and Auxiliary Results

2.1. Infinite System of Equations [16]

2.2. Quasi-Uniform Grid [8, 10]

3. Method of Infinite System for Stationary Problems

4. Parabolic Equation on Semi-Infinite Bar

5. The Equation of Complex Type

6. Concluding Remarks

Acknowledgments

References

Citing Literature

Figures

References

Related

Information