The reliable treatment of homotopy perturbation method (HPM) is applied to solve the Klein-Gordon partial differential equation of arbitrary (fractional) orders. This algorithm overcomes the difficulty that arises in calculating complicated integrals when solving nonlinear equations. Some numerical examples are presented to illustrate the efficiency of this technique.

1. Introduction

The Klein-Gordon equation plays a significant role in mathematical physics and many scientific applications such as solid-state physics, nonlinear optics, and quantum field theory [1, 2]. The equation has attracted much attention in studying solitons [3–6] and condensed matter physics, in investigating the interaction of solitons in a collisionless plasma, the recurrence of initial states, and in examining the nonlinear wave equations [7].

The HPM, proposed by He in 1998, has been the subject of extensive studies and was applied to different linear and nonlinear problems [8–13]. This method has the advantage of dealing directly with the problem without transformations, linearization, discretization, or any unrealistic assumption, and usually a few iterations lead to an accurate approximation of the exact solution [13]. The HPM has been used to solve nonlinear partial differential equations of fractional order (see, e.g., [14–16]). Some other methods for series solution that are used to solve nonlinear partial differential equations of fractional order include the Adomian decomposition method [17–19], the variational iteration method [20–22], and the homotopy analysis method [23–25].

Recently, Odibat and Momani [26] suggested a reliable algorithm for the HPM for dealing with nonlinear terms to overcome the difficulty arising in calculating complicated integrals. In [27], this algorithm is utilized to study the behavior of the nonlinear sine-Gordon equation with fractional time derivative. Our aim here is to apply the reliable treatment of HPM to obtain the solution of the initial value problem of the nonlinear fractional-order Klein-Gordon equation of the form

(1.1)

subjected to the initial condition

(1.2)

where

denotes the Caputo fractional derivative with respect to t of order α, u(x, t) is unknown function, and a, b, c, and γ are known constants with γ ∈ R, γ ≠ ±1.

2. Basic Definitions

Definition 2.1. A real function f(t), t > 0, is said to be in the space C_μ, μ ∈ ℝ, if there exists a real number p > μ, such that f(t) = t^pf₁(t), where f₁(t)∈C(0, ∞), and it is said to be in the space if f^(m) ∈ C_μ, m ∈ ℕ.

Definition 2.2. The Riemann-Liouville fractional integral operator of order α ≥ 0 of a function f(t) ∈ C_μ, μ ≥ −1 is defined as [28]

(2.1)

The operator J^α satisfy the following properties, for f ∈ C_μ, μ ≥ −1, α,β ≥ 0, and γ > −1:

(1)
J^αJ^βf(t) = J^α+βf(t),
(2)
J^αJ^βf(t) = J^βJ^αf(t),
(3)
J^αt^γ = (Γ(γ + 1)/Γ(γ + α + 1))t^α+γ.

Definition 2.3. The fractional derivative in Caputo sense of , m ∈ N, t > 0 is defined as

(2.2)

The operator D^β satisfy the following properties, for

, μ ≥ −1, and γ, β ≥ 0:

(1)
,
(2)
,
(3)
.

3. The Homotopy Perturbation Method (HPM)

Consider the following equation:

(3.1)

with boundary conditions

(3.2)

where A is a general differential operator, u(x, t) is the unknown function, and x and t denote spatial and temporal independent variables, respectively. B is a boundary operator, f(r) is a known analytic function, and Γ is the boundary of the domain Ω. The operator A can be generally divided into linear and nonlinear parts, say L and N. Therefore, (3.1) can be written as

(3.3)

In [9], He constructed a homotopy v(r, p) : Ω × [0,1] → R which satisfies

(3.4)

(3.5)

where p ∈ [0,1] is an embedding parameter,and u₀ is an initial guess of u(x, t) which satisfies the boundary conditions. Obviously, from (3.4) and (3.5), one has

(3.6)

Changing p from zero to unity is just that change of v(r, p) from u₀(r) to u(r). Expanding v(r, p) in Taylor series with respect to p, one has

(3.7)

Setting p = 1 results in the approximate solution of (3.1)

(3.8)

The reliable treatment of the classical HPM suggested by Odibat and Momani [26] is presented for nonlinear function N(u) which is assumed to be an analytic function and has the following Taylor series expansion:

(3.9)

According to [26], the following homotopy is constructed for (1.1):

(3.10)

The basic assumption is that the solution of (3.10) can be written as a power series in p,

(3.11)

Substituting (3.11) into (3.10) and equating the terms with identical powers of p, we obtain a series of linear equations in u₀, u_1,u₂, …, which can be solved by symbolic computation software. Finally, we approximate the solution

by the truncated series

(3.12)

4. Numerical Implementation

In this section, some numerical examples are presented to validate the solution scheme. Symbolic computations are carried out using Mathematica.

Example 4.1. Consider the fractional-order cubically nonlinear Klein-Gordon problem

(4.1)

with the exact solution u(x, t) = x^βt^α.

According to the homotopy (3.10), we obtain the following set of linear partial differential equations of fractional order:

(4.2)

Case 1 (α ∈ (1,2] and β = 2). Solving (4.2), we obtain

(4.3)

Figure 1 gives the comparison between the HPM 6th-order approximate solution of problem (4.1) in Case 1 with β = 2, α = 1.99,1.95,1.90, and 1.85 and the solution of corresponding problem of integer order denoted by u_2,2 at t = 0.5.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

u(x, 0.5) of Example 4.1 Case 1 for 6th-order HPM approximation as parameterized by α.

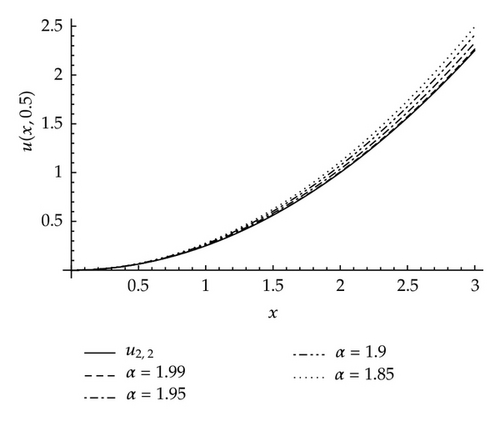
Case 2 (α = 2 and β ∈ (1,2]). Solving (4.2), we have

(4.4)

Figure 2 gives the comparison between the HPM 6th-order approximate solution of problem (4.1) in Case 2 with α = 2, β = 1.99, 1.95,1.90, and 1.85 and the solution of corresponding problem of integer order denoted by u_2,2 at t = 0.5.

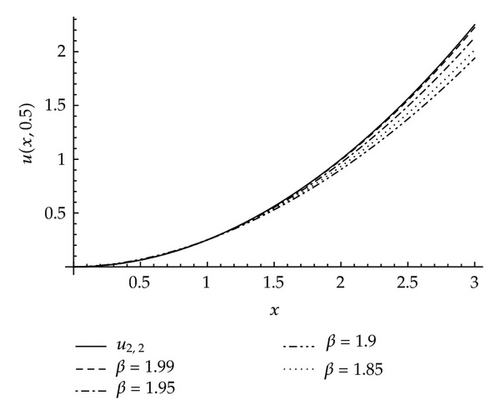
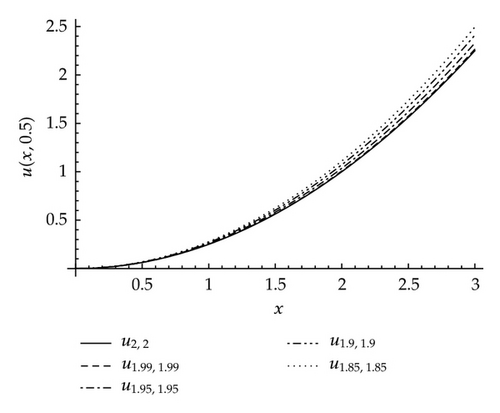
Case 3 (both α and β ∈ (1,2]). Solving (4.2), we have

(4.5)

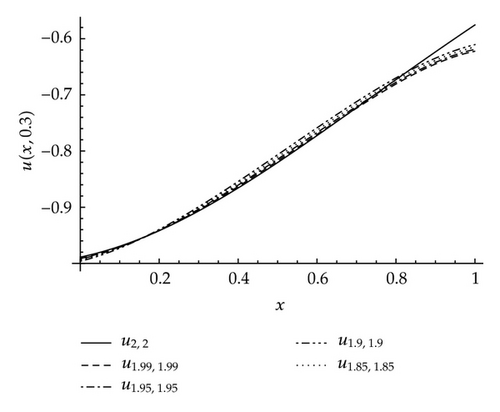
Figure 3 gives the comparison between the HPM 6th-order approximate solution of problem (4.1) in Case 3 with α and β taking the values 1.99,1.95,1.90, and 1.85 and the solution of corresponding problem of integer order denoted by u_2,2 at t = 0.5.

Example 4.2. Consider the fractional-order cubically nonlinear Klein-Gordon problem

(4.6)

The corresponding integer-order problem has the exact solution u_2,2 = −sech(x + t/2) [29].

According to the homotopy (3.10), we obtain the following set of linear partial differential equations of fractional order:

(4.7)

Case 1 (α ∈ (1,2] and β = 2). Solving (4.7), we have

(4.8)

and the solution is obtained as

(4.9)

Figure 4 gives the comparison between the HPM 4th-order approximate solution of problem (4.6) in Case 1 with β = 2, α = 1.99,1.95,1.90, and 1.85 and the solution of corresponding problem of integer order denoted by u_2,2 at t = 0.3.

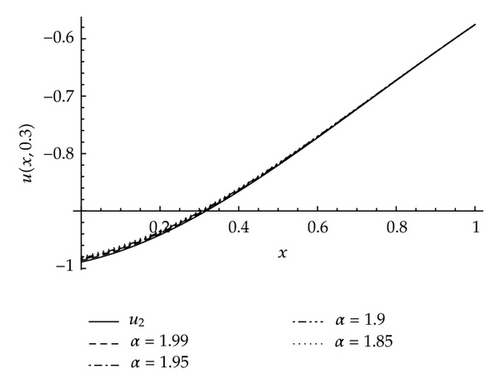
Case 2 (α = 2 and β ∈ (1,2]). As the attempt to evaluate Caputo fractional derivative of the functions sech(x) and tanh(x) yields hypergeometric function, we substitute sech(x) and tanh(x) by some terms of its Taylor series. Substituting the initial conditions and solving (4.7) for u₀, u₁, u₂, …, the components of the homotopy perturbation solution for (4.6) are derived as follows:

(4.10)

As the Caputo fractional derivative can not be evaluated for negative powers of the variable at hand, and noting that β ∈ (1,2], we can only evaluate the first two components of the series as illustrated. Thus, we suggest to generalize not only the derivatives in the integer-order problem to its fractional form, but also to generalize the conditions as well. For example, a generalized expansion of sech (x) in a fractional form can be written as

(4.11)

for which we have lim _β→2sech_β (x) = sech (x). Substituting the generalized form of the initial conditions and solving (4.7) for u₀, u₁, u₂, …, the components of the homotopy perturbation solution for this case are derived as follows:

(4.12)

and the solution is obtained as

(4.13)

Figure 5 gives the comparison between the HPM 4th-order approximate solution of problem (4.6) in Case 2 with α = 2, β = 1.99,1.95,1.90, and 1.85 and the solution of corresponding problem of integer order denoted by u_2,2 at t = 0.3.

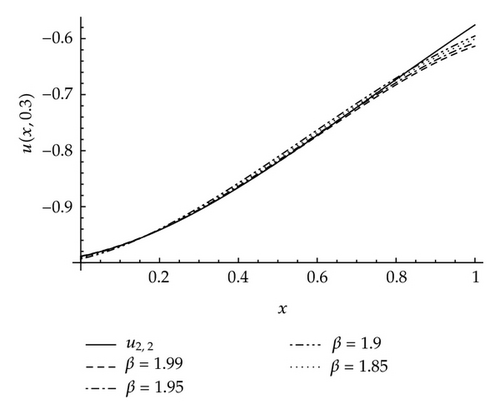
Case 3 (both α and β ∈ (1,2]). Carrying out the same procedure as in Case 2, we get

(4.14)

and the solution is thus obtained as

(4.15)

Figure 6 gives the comparison between the HPM 4th-order approximate solution of problem (4.6) in Case 3 with α, β = 1.99,1.95,1.90, and 1.85 and the solution of corresponding problem of integer order denoted by u_2,2 at t = 0.3.

5. Conclusion

The reliable treatment HPM is applied to obtain the solution of the Klien-Gordon partial differential equation of arbitrary (fractional) orders with spatial and temporal fractional derivatives. The main advantage of this algorithm is the capability to overcome the difficulty arising in calculating complicated integrals when dealing with nonlinear problems. The numerical examples carried out show good results, and their graphs illustrate the continuation of the solution of fractional-order Klien-Gordon equation to the solution of the corresponding second-order problem when the fractional-order parameters approach their integer limits.

References

1 Wazwaz A.-M., New travelling wave solutions to the Boussinesq and the Klein-Gordon equations, Communications in Nonlinear Science and Numerical Simulation. (2008) 13, no. 5, 889–901, https://doi.org/10.1016/j.cnsns.2006.08.005, 2372135.
10.1016/j.cnsns.2006.08.005
Web of Science® Google Scholar
2 Wazwaz A.-M., The tanh and the sine-cosine methods for compact and noncompact solutions of the nonlinear Klein-Gordon equation, Applied Mathematics and Computation. (2005) 167, no. 2, 1179–1195, https://doi.org/10.1016/j.amc.2004.08.006, 2169760.
10.1016/j.amc.2004.08.006
Web of Science® Google Scholar
3 Sassaman R. and Biswas A., Soliton solutions of the generalized Klein-Gordon equation by semi-inverse variational principle, Mathematics in Engineering, Science and Aerospace. (2011) 2, no. 1, 99–104.
Google Scholar
4 Sassaman R. and Biswas A., 1-soliton solution of the perturbed Klein-Gordon equation, Physics Express. (2011) 1, no. 1, 9–14.
CAS Google Scholar
5 Sassaman R., Heidari A., Majid F., Zerrad E., and Biswas A., Topological and non-topological solitons of the generalized Klein-Gordon equations in (1 + 2)-dimensions, Dynamics of Continuous, Discrete & Impulsive Systems A. (2010) 17, no. 2, 275–286, 2655931.
Google Scholar
6 Sassaman R. and Biswas A., Soliton perturbation theory for phi-four model and nonlinear Klein-Gordon equations, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 8, 3239–3249, https://doi.org/10.1016/j.cnsns.2008.12.020, 2502400.
10.1016/j.cnsns.2008.12.020
Web of Science® Google Scholar
7 El-Sayed S. M., The decomposition method for studying the Klein-Gordon equation, Chaos, Solitons and Fractals. (2003) 18, no. 5, 1025–1030, https://doi.org/10.1016/S0960%2D0779(02)00647%2D1, 1988710.
10.1016/S0960-0779(02)00647-1
Web of Science® Google Scholar
8 He J.-H., A coupling method of a homotopy technique and a perturbation technique for non-linear problems, International Journal of Non-Linear Mechanics. (2000) 35, no. 1, 37–43, https://doi.org/10.1016/S0020%2D7462(98)00085%2D7, 1723761.
10.1016/S0020-7462(98)00085-7
Web of Science® Google Scholar
9 He J.-H., Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering. (1999) 178, no. 3-4, 257–262, https://doi.org/10.1016/S0045%2D7825(99)00018%2D3, 1711041.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
10 He J.-H., Some asymptotic methods for strongly nonlinear equations, International Journal of Modern Physics B. (2006) 20, no. 10, 1141–1199, https://doi.org/10.1142/S0217979206033796, 2220565.
10.1142/S0217979206033796
Web of Science® Google Scholar
11 Ganji D. D. and Sadighi A., Application of He′s homotopy-perturbation method to nonlinear coupled systems of reaction diffusion equations, International Journal of Nonlinear Sciences and Numerical Simulation. (2006) 7, no. 4, 411–418.
10.1515/IJNSNS.2006.7.4.411
Web of Science® Google Scholar
12 Lu J., Analytical approach to Kawahara equation using variational iteration method and homotopy perturbation method, Topological Methods in Nonlinear Analysis. (2008) 31, no. 2, 287–294, 2432087.
Web of Science® Google Scholar
13 Yusufoglu E., Homotopy perturbation method for solving a nonlinear system of second order boundary value problems, International Journal of Nonlinear Sciences and Numerical Simulation. (2007) 8, no. 3, 353–358.
10.1515/IJNSNS.2007.8.3.353
Web of Science® Google Scholar
14 Yıldırım A., An algorithm for solving the fractional nonlinear Schrodinger equation by means of the homotopy perturbation method, International Journal of Nonlinear Sciences and Numerical Simulation. (2009) 10, no. 4, 445–450.
10.1515/IJNSNS.2009.10.4.445
CAS Web of Science® Google Scholar
15 Yıldırım A. and Koçak H., Homotopy perturbation method for solving the space-time fractional advection-dispersion equation, Advances in Water Resources. (2009) 32, no. 12, 1711–1716, https://doi.org/10.1016/j.advwatres.2009.09.003.
10.1016/j.advwatres.2009.09.003
Web of Science® Google Scholar
16 Wang Q., Homotopy perturbation method for fractional KdV-Burgers equation, Chaos, Solitons and Fractals. (2008) 35, no. 5, 843–850, https://doi.org/10.1016/j.chaos.2006.05.074, 2362643.
10.1016/j.chaos.2006.05.074
Web of Science® Google Scholar
17 Odibat Z. and Momani S., Numerical methods for nonlinear partial differential equations of fractional order, Applied Mathematical Modelling. (2008) 32, no. 1, 28–39, https://doi.org/10.1016/j.apm.2006.10.025.
10.1016/j.apm.2006.10.025
Web of Science® Google Scholar
18 Daftardar-Gejji V. and Bhalekar S., Solving multi-term linear and non-linear diffusion-wave equations of fractional order by Adomian decomposition method, Applied Mathematics and Computation. (2008) 202, no. 1, 113–120, https://doi.org/10.1016/j.amc.2008.01.027, 2437141.
10.1016/j.amc.2008.01.027
Web of Science® Google Scholar
19 Jafari H. and Daftardar-Gejji V., Solving linear and nonlinear fractional diffusion and wave equations by Adomian decomposition, Applied Mathematics and Computation. (2006) 180, no. 2, 488–497, https://doi.org/10.1016/j.amc.2005.12.031, 2270026.
10.1016/j.amc.2005.12.031
Web of Science® Google Scholar
20 Odibat Z. and Momani S., The variational iteration method: an efficient scheme for handling fractional partial differential equations in fluid mechanics, Computers & Mathematics with Applications. (2009) 58, no. 11-12, 2199–2208, https://doi.org/10.1016/j.camwa.2009.03.009, 2557350.
10.1016/j.camwa.2009.03.009
Web of Science® Google Scholar
21 Momani S., Odibat Z., and Alawneh A., Variational iteration method for solving the space- and time-fractional KdV equation, Numerical Methods for Partial Differential Equations. (2008) 24, no. 1, 262–271, https://doi.org/10.1002/num.20247, 2371359.
10.1002/num.20247
Web of Science® Google Scholar
22 Inc M., The approximate and exact solutions of the space- and time-fractional Burgers equations with initial conditions by variational iteration method, Journal of Mathematical Analysis and Applications. (2008) 345, no. 1, 476–484, https://doi.org/10.1016/j.jmaa.2008.04.007, 2422665.
10.1016/j.jmaa.2008.04.007
Web of Science® Google Scholar
23 Elsaid A., Homotopy analysis method for solving a class of fractional partial differential equations, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 9, 3655–3664, https://doi.org/10.1016/j.cnsns.2010.12.040, 2787812.
10.1016/j.cnsns.2010.12.040
Web of Science® Google Scholar
24 Dehghan M., Manafian J., and Saadatmandi A., Solving nonlinear fractional partial differential equations using the homotopy analysis method, Numerical Methods for Partial Differential Equations. (2010) 26, no. 2, 448–479, 2605472.
10.1002/num.20460
Web of Science® Google Scholar
25 Xu H., Liao S.-J., and You X.-C., Analysis of nonlinear fractional partial differential equations with the homotopy analysis method, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1152–1156, https://doi.org/10.1016/j.cnsns.2008.04.008, 2468947.
10.1016/j.cnsns.2008.04.008
Web of Science® Google Scholar
26 Odibat Z. and Momani S., A reliable treatment of homotopy perturbation method for Klein-Gordon equations, Physics Letters A. (2007) 365, no. 5-6, 351–357, https://doi.org/10.1016/j.physleta.2007.01.064, 2308777.
10.1016/j.physleta.2007.01.064
CAS Web of Science® Google Scholar
27 Elsaid A. and Hammad D. E., A reliable treatment of homotopy perturbation method for the sine-Gordon equation of arbitrary (fractional) order, Journal of Fractional Calculus and its Applications. (2012) 2, no. 1, 1–8.
Google Scholar
28 Podlubny I., Fractional Differential Equations, 1999, Academic Press, San Diego, Calif, USA, 1658022.
Web of Science® Google Scholar
29 Yusufoglu E., The variational iteration method for studying the Klein-Gordon equation, Applied Mathematics Letters. (2008) 21, no. 7, 669–674, https://doi.org/10.1016/j.aml.2007.07.023, 2423043.
10.1016/j.aml.2007.07.023
Web of Science® Google Scholar

Citing Literature

All articles

A Reliable Treatment of Homotopy Perturbation Method for Solving the Nonlinear Klein-Gordon Equation of Arbitrary (Fractional) Orders

Abstract

1. Introduction

2. Basic Definitions

3. The Homotopy Perturbation Method (HPM)

4. Numerical Implementation

5. Conclusion

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Reliable Treatment of Homotopy Perturbation Method for Solving the Nonlinear Klein-Gordon Equation of Arbitrary (Fractional) Orders

Abstract

1. Introduction

2. Basic Definitions

3. The Homotopy Perturbation Method (HPM)

4. Numerical Implementation

5. Conclusion

References

Citing Literature

Figures

References

Related

Information