Discrete Dynamics in Nature and Society
Volume 2012, Issue 1 579431
Research Article
Open Access

Numerical Treatment of Singularly Perturbed Two-Point Boundary Value Problems by Using Differential Transformation Method

Nurettin Doğan, 

Corresponding Author

Nurettin Doğan

Department of Computer Engineering, Faculty of Technology, Gazi University, Teknikokullar, 06500 Ankara, Turkey gazi.edu.tr

Search for more papers by this author
Vedat Suat Ertürk, 

Vedat Suat Ertürk

Department of Mathematics, Faculty of Arts and Sciences, Ondokuz Mayıs University, 55139 Samsun, Turkey omu.edu.tr

Search for more papers by this author
Ömer Akın, 

Ömer Akın

Department of Mathematics, Faculty of Arts and Sciences, TOBB University of Economics and Technology, Söğütözü, 06530 Ankara, Turkey etu.edu.tr

Search for more papers by this author
First published: 26 April 2012
https://doi.org/10.1155/2012/579431
Citations: 9
Academic Editor: Garyfalos Papaschinopoulos

Abstract

Differential transform method is adopted, for the first time, for solving linear singularly perturbed two-point boundary value problems. Four numerical examples are given to demonstrate the effectiveness of the present method. Results show that the numerical scheme is very effective and convenient for solving a large number of linear singularly perturbed two-point boundary value problems with high accuracy.

1. Introduction

Singularly perturbed second-order two-point boundary value problems, which received a significant amount of attention in past and recent years, arise very frequently in fluid mechanics, quantum mechanics, optimal control, chemical-reactor theory, aerodynamics, reaction-diffusion process, geophysics, and so forth. In these problems a small parameter multiplies to a highest derivative. A well-known fact is that the solution of such problems display sharp boundary or interior layers when the singular perturbation parameter ε is very small. Numerically, the presence of the perturbation parameter leads to difficulties when classical numerical techniques are used to solve such problems, and convergence will not be uniform. The solution varies rapidly in some parts and varies slowly in some other parts. There are thin transition boundary or interior layers where the solutions can change rapidly, while away from the layers the solution behaves regularly and varies slowly. There are a wide variety of techniques for solving singular perturbation problems (see [1–7]). Furthermore different numerical methods have been proposed by various authors for singularly perturbed two-point boundary value problems, such as non-uniform mesh tension spline methods [8], non-uniform mesh compression spline numerical method [9], and the least squares methods based on the Bézier control points [10].

The aim of our study is to introduce the differential transform method [11] as an alternative to existing methods in solving singularly perturbed two-point boundary value problems and the method is implemented to four numerical examples. The present method is the first time applied by the authors to singularly perturbed two-point boundary value problems.

The rest of the paper is organized as follows. In Section 2, we give a brief description of the method. In Section 3, we have solved four numerical examples to demonstrate the applicability of the present method. The discussion on our results is given in Section 4.

2. Fundamental of Differential Transform Method

In this section, the concept of the differential transformation method (DTM) is briefly introduced. The concept of differential transform was first introduced by Pukhov [11], who solved linear and nonlinear initial value problems in electric circuit analysis. This method constructs, for differential equations, an analytical solution in the form of a polynomial. It is a seminumerical and semianalytic technique that formulizes the Taylor series in a totally different manner. The Taylor series method is computationally taken long time for large orders. With this technique, the given differential equation and its related boundary conditions are transformed into a recurrence equation that finally leads to the solution of a system of algebraic equations as coefficients of a power series solution. This method is useful to obtain exact and approximate solutions of linear and nonlinear differential equations. No need to linearization or discretization, large computational work and round-off errors are avoided. It has been used to solve effectively, easily, and accurately a large class of linear and nonlinear problems with approximations. The method is well addressed in [12–19]. The basic principles of the differential transformation method can be described as follows.

The differential transform of the kth derivative of a function f(x) is defined as follows.
(2.1)
and the differential inverse transform of F(k) is defined as follows:
(2.2)
In real applications, function f(x) is expressed by a finite series and (2.2) can be written as
(2.3)
The following theorems that can be deduced from (2.1) and (2.2) are given [20].

Theorem 2.1. If f(x) = g(x) ± h(x), then F(k) = G(k) ± H(k).

Theorem 2.2. If f(x) = ag(x), then F(k) = aG(k), where a is constant.

Theorem 2.3. If f(x) = (dmg(x)/dxm), then F(k) = ((m + k)!/k!)G(k + m).

Theorem 2.4. If f(x) = g(x)h(x), then .

Theorem 2.5. If f(x) = xn, then

(2.4)
Here n ∈ N, N is the set of natural numbers, and W(k) is the differential transform function of w(x). In the case of x0 = 0, one has the following result:
(2.5)

Theorem 2.6. If f(x) = g1(x)g2(x) ⋯ gn−1(x)gn(x), then

(2.6)

3. The Applications of Differential Transformation Method and Numerical Results

In order to evaluate the accuracy of DTM for solving singularly perturbed two-point boundary value problems, we will consider the following examples. These examples have been chosen because they have been widely discussed in the literature and also approximate solutions are available for a concrete comparison.

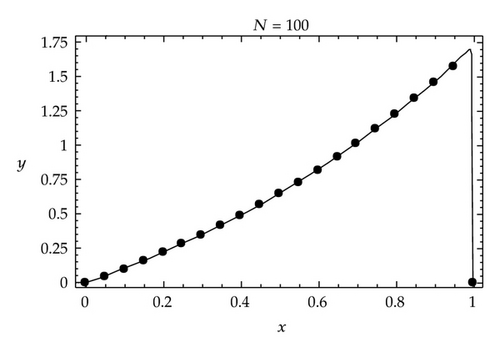
Example 3.1. We first consider the following problem [21]:

(3.1)
with the boundary conditions
(3.2)
The exact solution for this problem is
(3.3)
Taking the differential transform of both sides of (3.1), the following recurrence relation is obtained:
(3.4)
The boundary conditions given in (3.2) can be transformed at x0 = 0 as follows:
(3.5)
Using (3.4) and (3.5) and by taking N = 5, the following series solution is obtained:
(3.6)
where, according to (2.1), a = y′(0). The constant a is evaluated from the second boundary condition given in (3.2) at x = 1 as follows:
(3.7)
Then, by using the inverse transform rule in (2.2), we get the following series solution:
(3.8)
The evolution results for the exact solution (3.3) and the approximate solution (3.8) obtained by using the differential transform method, for ε = 2−9, are shown in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The approximate solution (dotted curve) versus the analytic solution (solid curve) for ε = 2−9.

Example 3.2. Secondly, we consider the following problem:

(3.9)
with the boundary conditions
(3.10)
The exact solution for this boundary value problem is
(3.11)
Taking the differential transform of (3.9), we have
(3.12)
Choosing x0 = 0, the boundary conditions given in (3.10) can be transformed to give
(3.13)
By using (3.12) and (3.13), and, by taking N = 5, we get the following series solution:
(3.14)
where, according to (2.1), a = y′(0).

The constant a is evaluated from the second boundary condition given in (3.10) at x = 1 as follows:

(3.15)

Then, by using the inverse transform rule in (2.2), one can obtain the approximate solution. We do not give it because of long terms in the approximate solution.

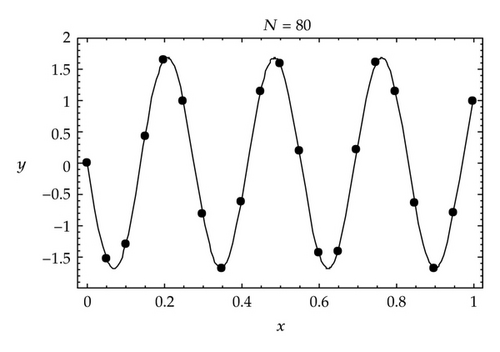
In Figure 2, we plot the exact solution (3.11) and the approximate solution for ε = 10−3.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The approximate solution (dotted curve) versus the analytic solution (solid curve) for ε = 10−3.

Example 3.3. Thirdly, we consider the following problem [22]

(3.16)
subject to the boundary conditions
(3.17)
The exact solution for this problem is
(3.18)
Applying the operations of the differential transform to (3.16), we obtain the following recurrence relation:
(3.19)
By using the basic definitions of the differential transform and (3.17), the following transformed boundary conditions at x0 = 0 can be obtained:
(3.20)
By utilizing the recurrence relation in (3.19) and the transformed boundary conditions in (3.20), the following series solution up to 15-term is obtained:
(3.21)
where a = y′(0).

By taking N = 15, the following equation can be obtained from (3.20):

(3.22)

From (3.22), a is evaluated as

(3.23)
By using this value of the missing boundary condition, the approximate solution can be obtained easily.

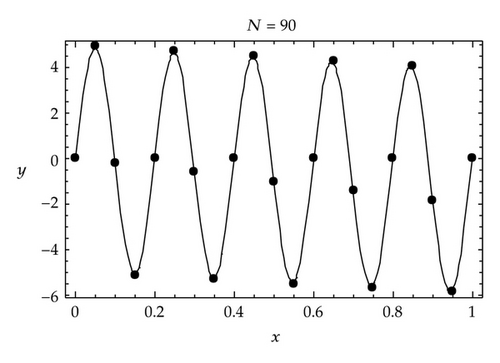
Comparison of the approximate solution with the exact solution (3.18) for ε = 2−5 is sketched in Figure 3.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The approximate solution (dotted curve) versus the analytic solution (solid curve) for ε = 2−5.

Example 3.4. Finally, we consider the following problem [23, 24]

(3.24)
subject to the boundary conditions
(3.25)
Its exact solution is given by
(3.26)
By applying the fundamental mathematical operations performed by differential transform, the differential transform of (3.24) is obtained as
(3.27)
The boundary conditions in (3.25) can be transformed at x0 = 0 as
(3.28)
By using the inverse transformation rule in (2.2), the approximate solution is evaluated up to N = 20. The first few terms of the series solution are given by
(3.29)
where a = y′(0).The solution obtained from (2.3) has yet to satisfy the second boundary condition in (3.25), which has not been manipulated in obtaining this approximate solution. Applying this boundary condition and then solving the resulting equation for a will determine the unknown constant a and eventually the numerical solution.

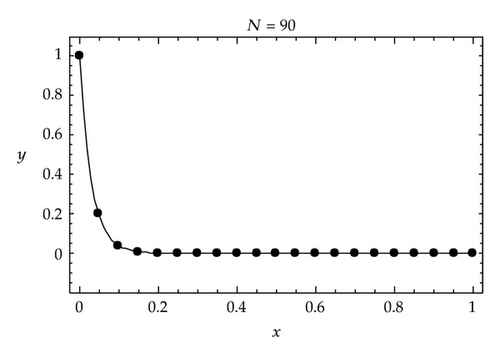
Graphical result for ε = 1/1000 with comparison to the exact solution (3.26) is shown in Figure 4.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The approximate solution (dotted curve) versus the analytic solution (solid curve) for ε = 1/1000.

4. Conclusion

In this study, the differential transformation method (DTM) has been employed, for the first time, successfully for solving linear singularly perturbed two-point boundary value problems. Four examples with boundary layers have been treated. This new method accelerated the convergence to the solutions. As it can be seen, this method leads to tremendously accurate results. It provides the solutions in terms of convergent series with easily computable components in a direct way without using linearization, discretization, or restrictive assumptions. The Mathematica software system has been used for all the symbolic and numerical computations in this paper.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.