Journal of Applied Mathematics
Volume 2012, Issue 1 569098
Research Article
Open Access

Solitonic Solutions for Homogeneous KdV Systems by Homotopy Analysis Method

Mohammed Ali, 

Corresponding Author

Mohammed Ali

Department of Mathematics and Statistics, Jordan University of Science and Technology, Irbid 22110, Jordan just.edu.jo

Search for more papers by this author
Marwan Alquran, 

Marwan Alquran

Department of Mathematics and Statistics, Jordan University of Science and Technology, Irbid 22110, Jordan just.edu.jo

Search for more papers by this author
Mahmoud Mohammad, 

Mahmoud Mohammad

Department of Mathematics and Statistics, Jordan University of Science and Technology, Irbid 22110, Jordan just.edu.jo

Search for more papers by this author
First published: 04 October 2012
https://doi.org/10.1155/2012/569098
Citations: 5
Academic Editor: J. C. Butcher

Abstract

We study two-component evolutionary systems of a homogeneous KdV equations of second and third order. The homotopy analysis method (HAM) is used for analytical treatment of these systems. The auxiliary parameter h of HAM is freely chosen from the stability region of the h-curve obtained for each proposed system.

1. Introduction

Applications in physics are modeled by nonlinear systems. Very few nonlinear systems have closed form solutions, therefore, many researchers stress their goals to search numerical solutions. Homotopy analysis method (HAM), first proposed by Liao [1], is an elegant method which has proved its effectiveness and efficiency in solving many types of nonlinear equations [2, 3]. Liao in his book [4] proved that HAM is a generalization of some previously used techniques such as the d-expansion method, artificial small parameter method [5], and Adomian decomposition method. Moreover, unlike previous analytic techniques, the HAM provides a convenient way to adjust and control the region and rate of convergence [6]. Recently, new interested applications of the homotopy analysis have been introduced by Abbasbandy and coauthors [7, 8]. Also, in [9] HAM is used to study the effects of thermocapillarity and thermal radiation on flow and heat transfer in a thin liquid film.

In this work, we consider a two-component evolutionary system of a homogeneous KdV equations of third order type (I) and (II) given, respectively, by
()
()
Also, we study a two-component evolutionary system of a homogeneous KdV equations of second order given by
()
In the literature many other direct mathematical methods such as the sine-cosine method, rational sine-cosine method, and extended tanh-coth method [10–14] have been implemented in obtaining different solitonic solutions to these systems. Our main goal in this paper is to see how much accuracy we may gain by applying HAM to such evolutionary systems.

In what follows, we highlight the main features of the homotopy analysis method. More details and examples can be found in [7, 8, 15] and the references therein.

2. Survey of Homotopy Analysis Method

To illustrate the basic ideas of this method, we consider the following nonlinear system of differential equations:
()
where Nj are nonlinear operators, t is an independent variable, ui(t) are unknown functions. By means of generalizing the traditional homotopy method, Liao construct the zeroth-order deformation equation as follows:
()
where i = 1, …, m,   j = 1, …, n, q    ϵ    [0,1] is an embedding parameter,  Lj is a general differential linear operator, ui,0(x, t) are initial guesses of ui(x, t),  ϕi(x, t, q) are unknown functions, and h and H(x, t) are auxiliary parameter and auxiliary function, respectively. It is important note that, one has great freedom to choose auxiliary objects such as h and Lj in HAM; this freedom plays an important role in establishing the key stone of validity and flexibility of HAM as shown in this paper. obviously, when q = 0 and q = 1, both
()
thus as q increasing from 0 to 1, the solutions of ϕi(x, t, q) change from the initial guesses ui,0(x, t) to the solutions ui(x, t). Expanding ϕi(x, t, q) in Taylor series with respect to q, one has
()
where
()
if the auxiliary linear operators, the initial guesses, the auxiliary parameter h, and the auxiliary function are so properly chosen, then the series (2.4) converges at q = 1, then one has
()
which must be one of the solutions of the original nonlinear equations, as proved by liao. Define the vector
()
Differentiating (2.2), k times with respect to the embedding parameter q and then setting q = 0 and finally dividing them by k!, we have the so-called kth-order deformation equation
()
subject to the initial conditions
()
where
()
It should be emphasized that ui,k(x, t) for m ≥ 1 is governed by the linear equation (2.8) under the linear boundary conditions that come from original problem, which can be easily solved by symbolic computation software such as Mathematica. When h = −1, and H(x, t) = 1 (2.2) becomes
()
which is used mostly in the homotopy perturbation method [16–20].

For the following numerical examples, we use Lj = ∂/∂t; H(x, t) = 1.

3. Two-Component Evolutionary System of Order 3: Type I

In this section, we consider system (1.1)
()
subject to
()
For application of the homotopy analysis method, we choose the initial approximations as
()
Employing HAM with the mentioned parameters in Section 2, we have the following zero-order deformation equations:
()
Subsequently solving the Nth order deformation equations, we obtain
()
We use an 10-term approximation and set
()
Comments and illustrations upon the obtained results can be observed in Figures 1 and 2.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
(a) The h curve of system (1.1) for u(3,1) obtained from the 10th order HAM. (b) The h curve of system (1.1) for v(3,1) obtained from the 10th order HAM.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
(a) The h curve of system (1.1) for u(3,1) obtained from the 10th order HAM. (b) The h curve of system (1.1) for v(3,1) obtained from the 10th order HAM.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
(a) The obtained uHAM for system (1.1) using 10-term approximation. (b) The obtained vHAM for system (1.1) using 10-term approximation. h = −1.1.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
(a) The obtained uHAM for system (1.1) using 10-term approximation. (b) The obtained vHAM for system (1.1) using 10-term approximation. h = −1.1.

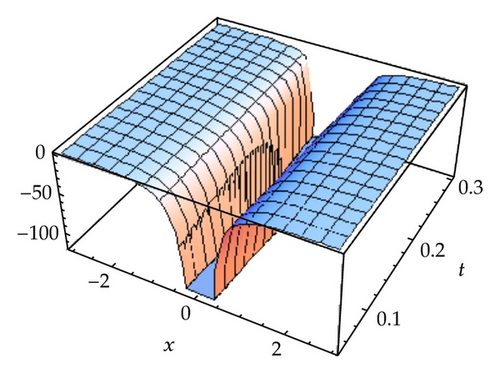
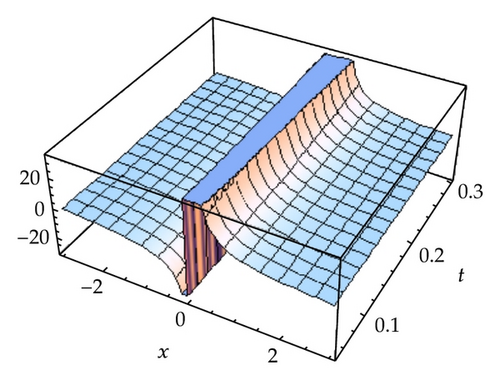
4. Two-Component Evolutionary System of Order 3: Type II

In this section, we consider system (1.2)
()
subject to
()
For application of the homotopy analysis method, we choose the initial approximations as
()
Employing HAM with mentioned parameters in Section 2, we have the following zero-order deformation equations:
()
Subsequently solving the Nth order deformation equations, we obtain
()
and so on. We use an 10-term approximation and set
()
Comments and illustrations upon the obtained results can be observed in Figures 3 and 4.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
(a) The h curve of system (1.2) for u(5,1) obtained from the 10th order HAM. (b) The h curve of system (1.2) for v(5,1) obtained from the 10th order HAM.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
(a) The h curve of system (1.2) for u(5,1) obtained from the 10th order HAM. (b) The h curve of system (1.2) for v(5,1) obtained from the 10th order HAM.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
(a) The obtained uHAM for system (1.2) using 10-term approximation. (b) The obtained vHAM for system (1.2) using 10-term approximation. h = −1.3.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
(a) The obtained uHAM for system (1.2) using 10-term approximation. (b) The obtained vHAM for system (1.2) using 10-term approximation. h = −1.3.

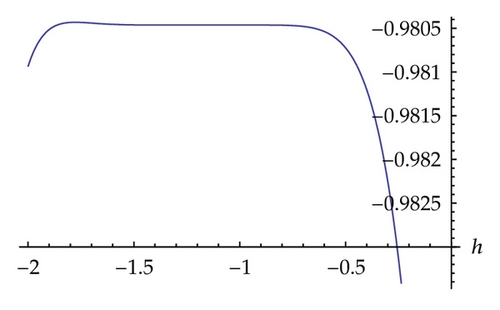
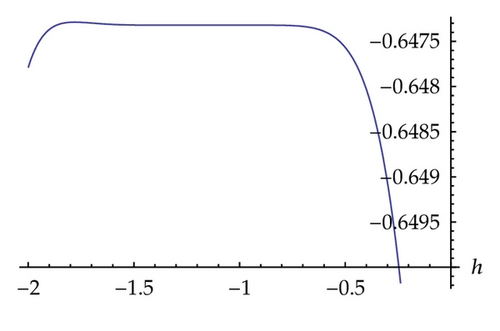
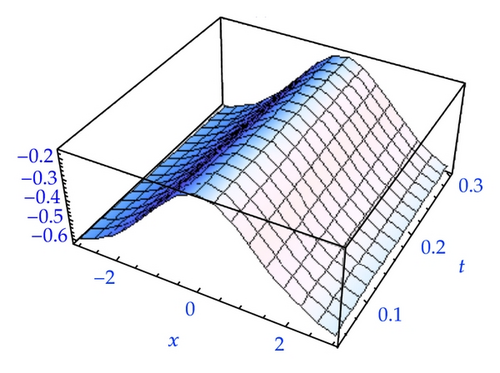
5. Two-Component Evolutionary System of Order 2

In this section, we consider system (1.3)
()
subject to
()
We proceed in the same manner and choose the initial approximations as
()
The zero-order deformation equations are
()
Subsequently, we obtain
()
and so on. We use an 11-term approximation and set
()
The obtained h-curve and the HAM solutions of u(x, t) and v(x, t) are given in Figures 5 and 6.
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
(a) The h curve of system (1.3) for u(3,1) obtained from the 10th order HAM. (b) The h curve of system (1.3) for v(3,1) obtained from the 10th order HAM.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
(a) The h curve of system (1.3) for u(3,1) obtained from the 10th order HAM. (b) The h curve of system (1.3) for v(3,1) obtained from the 10th order HAM.
Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
(a) The obtained uHAM for system (1.3) using 10-term approximation. (b) The obtained vHAM for system (1.3) using 10-term approximation. h = −0.7.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
(a) The obtained uHAM for system (1.3) using 10-term approximation. (b) The obtained vHAM for system (1.3) using 10-term approximation. h = −0.7.

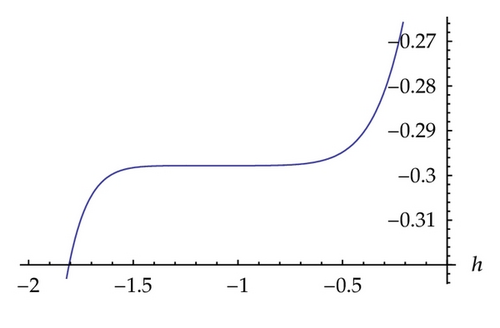
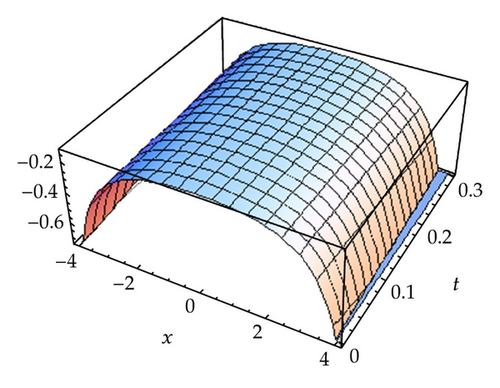
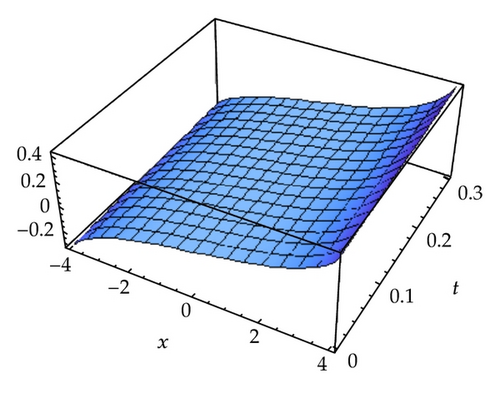
6. Discussion and Concluding Remarks

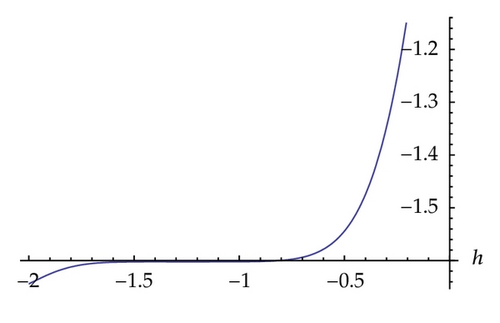
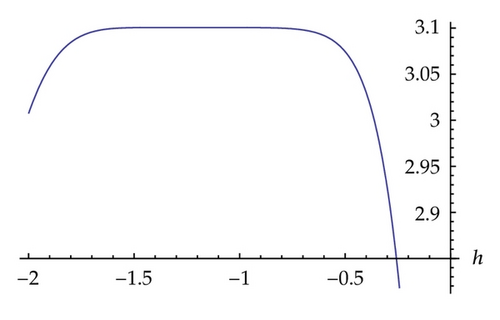
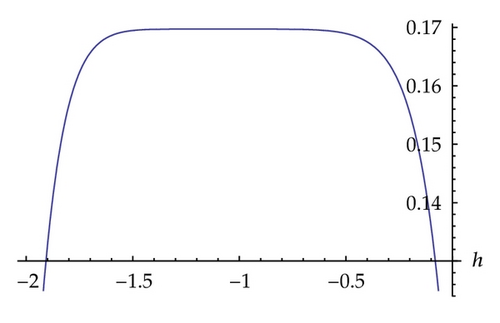
In this paper, we obtained soliton solutions for homogeneous KdV systems of second and third order by means of homotopy analysis method. The convergence region for the obtained, approximation, is determined by the parameter h as shown in Figures 1, 3, and 5, respectively, for systems ((1.1), (1.2), and (1.3)).

Homotopy analysis method provides us a convenient freely chosen with parameter h in contrast to the Homotopy perturbation method, where h is assumed to be −1. In this work, h has been chosen to be −1.1,    − 1.3,   and     − 0.7, respectively, for systems ((1.1), (1.2), and (1.3)). It is worth noting that the choice of the parameter h in this paper is considered based on the obtained stability region of the h-curve for each system; for example, in system (1.1) the stability region of h falls between −1.5 and −0.7 and we considered the midpoint of this interval.

Finally, the absolute errors for the obtained approximate solution of system (1.1) are given in Tables 1 and 2.

Table 1. Absolute errors regarding u(x, t) for system (1.1) with N = 10.
xi | tj 0.05 0.1 0.15 0.20 0.25 0.30
−6 4.32 × 10−13 4.09 × 10−12 2.05 × 10−11 7.48 × 10−11 2.24 × 10−10 5.86 × 10−10
−4 7.77 × 10−12 7.78 × 10−11 4.14 × 10−10 1.61 × 10−9 5.16 × 10−9 1.44 × 10−8
−2 3.43 × 10−10 6.30 × 10−9 5.54 × 10−8 3.25 × 10−7 1.46 × 10−6 5.40 × 10−6
2 1.25 × 10−12 1.99 × 10−12 1.92 × 10−12 5.76 × 10−12 1.29 × 10−11 1.98 × 10−11
4 9.23 × 10−14 1.59 × 10−13 5.30 × 10−14 4.45 × 10−13 3.79 × 10−13 7.06 × 10−13
6 5.52 × 10−15 9.60 × 10−15 2.88 × 10−15 2.67 × 10−14 2.02 × 10−14 4.30 × 10−14
Table 2. Absolute errors regarding v(x, t) for system (1.1) with N = 10.
xi | tj 0.05 0.1 0.15 0.20 0.25 0.30
−6 2.67 × 10−12 1.51 × 10−11 5.27 × 10−11 1.45 × 10−10 3.46 × 10−10 7.47 × 10−10
−4 1.17 × 10−11 7.21 × 10−11 2.81 × 10−10 8.87 × 10−10 2.44 × 10−9 6.15 × 10−9
−2 1.22 × 10−10 1.62 × 10−9 1.21 × 10−8 6.42 × 10−8 2.68 × 10−7 9.44 × 10−7
2 6.19 × 10−13 3.18 × 10−12 5.02 × 10−13 6.58 × 10−12 1.03 × 10−11 2.23 × 10−12
4 1.61 × 10−13 7.90 × 10−13 8.33 × 10−14 1.39 × 10−12 1.70 × 10−12 3.50 × 10−13
6 3.93 × 10−14 1.92 × 10−13 2.42 × 10−14 3.34 × 10−13 4.01 × 10−13 1.00 × 10−13

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.